Consider a numerical valued random phenomenon, with probability function \(P[\cdot]\) . The probability function \(P[\cdot]\) determines a distribution of a unit mass on the real line, the amount of which lying on any (Borel) set \(B\) of real numbers is equal to \(P[B]\) . In order to summarize the characteristics of \(P[\cdot]\) by a few numbers, we define in this section the notion of the expectation of a continuous function \(g(x)\) of a real variable \(x\) , with respect to the probability function \(P[\cdot]\) , to be denoted by \(E[g(x)]\) . It will be seen that the expectation \(E[g(x)]\) has much the same properties as the average of \(g(x)\) , with respect to a set of numbers.
For the case in which the probability function \(P[\cdot]\) is specified by a probability mass function \(p(\cdot)\) , we define, in analogy with (1.12) , \[E[g(x)]=\sum_{\substack{\text { over all } x \text { such } \\ \text { that } p(x)>0}} g(x) p(x). \tag{2.1}\]
The sum written in (2.1) may involve the summation of a countably infinite number of terms and therefore is not always meaningful. For reasons made clear in section 1 of Chapter 8 the expectation \(E[g(x)]\) is said to exist if \[E[|g(x)|]=\sum_{\substack{\text { over all } x \text { such } \\ \text { that } p(x)>0}}|g(x)| p(x)<\infty, \tag{2.2}\] In words, the expectation \(E[g(x)]\) , defined in (2.1), exists if and only if the infinite series defining \(E[g(x)]\) is absolutely convergent . A test for convergence of an infinite series is given in theoretical exercise 2.1 .
For the case in which the probability function \(P[\cdot]\) is specified by a probability density function \(f(\cdot)\) , we define \[E[g(x)]=\int_{-\infty}^{\infty} g(x) f(x) dx. \tag{2.3}\]
The integral written in (2.3) is an improper integral and therefore is not always meaningful. Before one can speak of the expectation \(E[g(x)]\) , one must verify its existence. The expectation \(E[g(x)]\) is said to exist if \[E[|g(x)|]=\int_{-\infty}^{\infty}|g(x)| f(x) d x<\infty. \tag{2.4}\] In words, the expectation \(E[g(x)]\) defined in exists if and only if the improper integral defining \(E[g(x)]\) is absolutely convergent . In the case in which the functions \(g(\cdot)\) and \(f(\cdot)\) are continuous for all (but a finite number of values of) \(x\) , the integral in (2.3) may be defined as an improper Riemann 1 integral by the limit
\[\int_{-\infty}^{\infty} g(x) f(x) d x=\lim _{\substack{a \rightarrow-\infty \\ b \rightarrow \infty}} \int_{a}^{b} g(x) f(x) dx. \tag{2.5}\]
A useful tool for determining whether or not the expectation \(E[g(x)]\) , given by (2.3) , exists is the test for convergence of an improper integral given in theoretical exercise 2.1 .
A discussion of the definition of the expectation in the case in which the probability function must be specified by the distribution function is given in section 6 .
The expectation \(E[g(x)]\) is sometimes called the ensemble average of the function \(g(x)\) in order to emphasize that the expectation (or ensemble average) is a theoretically computed quantity. It is not an average of an observed set of numbers, as was the case in section 1 . We shall later consider averages with respect to observed values of random phenomena, and these will be called sample averages.
A special terminology is introduced to describe the expectation \(E[g(x)]\) of various functions \(g(x)\) .
We call \(E[x]\) , the expectation of the function \(g(x)=x\) with respect to a probability law, the mean of the probability law . For a discrete probability law, with probability mass function \(p(\cdot)\) ,
\[E[x]=\sum_{\substack{\text { over anl } x \text { such } \\ \text { that } p(x)>0}} x p(x). \tag{2.6}\]
For a continuous probability law, with probability density function \(f(\cdot)\) ,
\[E[x]=\int_{-\infty}^{\infty} x f(x) dx. \tag{2.7}\]
It may be shown that the mean of a probability law has the following meaning. Suppose one makes a sequence \(X_{1}, X_{2}, \ldots, X_{n}, \ldots\) of independent observations of a random phenomenon obeying the probability law and forms the successive arithmetic means
\[\begin{gather} A_{1}=X_{1}, \quad A_{2}=\frac{1}{2}\left(X_{1}+X_{2}\right), \\ A_{3}=\frac{1}{3}\left(X_{1}+X_{2}+X_{3}\right), \ldots, \quad A_{n}=\frac{1}{n}\left(X_{1}+X_{2}+\cdots+X_{n}\right), \cdots \end{gather}\]
These successive arithmetic means, \(A_{1}, A_{2}, \ldots, A_{n}\) , will (with probability one) tend to a limiting value if and only if the mean of the probability law is finite. Further, this limiting value will be precisely the mean of the probability law.
We call \(E\left[x^{2}\right]\) , the expectation of the function \(g(x)=x^{2}\) with respect to a probability law, the mean square of the probability law . This notion is not to be confused with the square mean of the probability law , which is the square \((E[x])^{2}\) of the mean and which we denote by \(E^{2}[x]\) . For a discrete probability law, with probability mass function \(p(\cdot)\) ,
\[E\left[x^{2}\right]=\sum_{\substack{\text { over all } x \text { such } \\ \text { that } p(x)>0}} x^{2} p(x). \tag{2.8}\]
For a continuous probability law, with probability density function \(f(\cdot)\) ,
\[E\left[x^{2}\right]=\int_{-\infty}^{\infty} x^{2} f(x) dx. \tag{2.9}\]
More generally, for any integer \(n=1,2,3, \ldots\) , we call \(E\left[x^{n}\right]\) , the expectation of \(g(x)=x^{n}\) with respect to a probability law, the nth moment of the probability law . Note that the first moment and the mean of a probability law are the same; also, the second moment and the mean square of a probability law are the same.
Next, for any real number \(c\) , and integer \(n=1,2,3, \ldots\) , we call \(E\left[(x-c)^{n}\right]\) the nth moment of the probability law about the point \(c\) . Of especial interest is the case in which \(c\) is equal to the mean \(E[x]\) . We call \(E\left[(x-E[x])^{n}\right]\) the nth moment of the probability law about its mean or, more briefly, the nth central moment of the probability law.
The second central moment \(E\left[(x-E[x])^{2}\right]\) is especially important and is called the variance of the probability law . Given a probability law, we shall use the symbols \(m\) and \(\sigma^{2}\) to denote, respectively, its mean and variance; consequently,
\[m=E[x], \quad \sigma^{2}=E\left[(x-m)^{2}\right]. \tag{2.10}\]
The square root \(\sigma\) of the variance is called the standard deviation of the probability law. The intuitive meaning of the variance is discussed in section 4 .
Example 2A . The normal probability law with parameters \(m\) and \(\sigma\) is specified by the probability density function \(f(\cdot)\) , given by (4.11) of Chapter 4. Its mean is equal to \[E[x]=\frac{1}{\sigma \sqrt{2 \pi}} \int_{-\infty}^{\infty} x e^{-1 / 2\left(\frac{x-m}{\sigma}\right)^{2}} d x=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty}(m+\sigma y) e^{-1 / 2 y^{2}} dy, \tag{2.11}\] where we have made the change of variable \(y=(x-m) / \sigma\) . Now
\[\int_{-\infty}^{\infty} e^{-1 / 2 y^{2}} d y=\int_{-\infty}^{\infty} y^{2} e^{-1 / 2 y^{2}} d y=\sqrt{2 \pi}, \quad \int_{-\infty}^{\infty} y e^{-1 / 2 y^{2}} d y=0. \tag{2.12}\]
Equation (2.12) follows from (2.20) and (2.22) of Chapter 4 and the fact that for any integrable function \(h(y)\) \begin{align} & \int_{-\infty}^{\infty} h(y) d y=0 \quad \text { if } h(-y)=-h(y) \\ & \int_{-\infty}^{\infty} h(y) d y=2 \int_{0}^{\infty} h(y) d y \quad \text { if } h(-y)=h(y). \tag{2.13} \end{align}
From (2.12) and (2.13) it follows that the mean \(E[x]\) is equal to \(m\) . Next, the variance is equal to \begin{align} E\left[(x-m)^{2}\right]=\frac{1}{\sigma \sqrt{2 \pi}} \int_{-\infty}^{\infty}(x & -m)^{2} e^{-1 / 2\left(\frac{x-m}{\sigma}\right)^{2}} d x \tag{2.14} \\ & =\sigma^{2} \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} y^{2} e^{-1 / 2 y^{2}} d y=\sigma^{2}. \end{align} Notice that the parameters \(m\) and \(\sigma\) in the normal probability law were chosen equal to the mean and standard deviation of the probability law.
The operation of taking expectations has certain basic properties with which one may perform various formal manipulations. To begin with, we have the following properties for any constant \(c\) and any functions \(g(x), g_{1}(x)\) , and \(g_{2}(x)\) whose expectations exist: \[E[c] =c. \tag{2.15}\] \[E[c g(x)] =c E[g(x)]. \tag{2.16}\] \[E\left[g_{1}(x)+g_{2}(x)\right] =E\left[g_{1}(x)\right]+E\left[g_{2}(x)\right]. \tag{2.17}\] \[E\left[g_{1}(x)\right] \leq E\left[g_{2}(x)\right] \quad \text { if } g_{1}(x) \leq g_{2}(x) \quad \text { for all } x. \tag{2.18}\] \[|E[g(x)]| \leq E[|g(x)|]. \tag{2.19}\] In words, the first three of these properties may be stated as follows: the expectation of a constant \(c\) [that is, of the function \(g(x)\) , which is equal to \(c\) for every value of \(x\) ] is equal to \(c\) ; the expectation of the product of a constant and a function is equal to the constant multiplied by the expectation of the function; the expectation of a function which is the sum of two functions is equal to the sum of the expectations of the two functions.
Equations (2.15) to (2.19) are immediate consequences of the definition of expectation. We write out the details only for the case in which the expectations are taken with respect to a continuous probability law with probability density function \(f(\cdot)\) . Then, by the properties of integrals,
\[\begin{gather} E[c]=\int_{-\infty}^{\infty} c f(x) d x=c \int_{-\infty}^{\infty} f(x) d x=c, \\ E[c g(x)]=\int_{-\infty}^{\infty} c g(x) f(x) d x=c \int_{-\infty}^{\infty} g(x) f(x) d x=c E[g(x)], \\ E\left[g_{1}(x)+g_{2}(x)\right]=\int_{-\infty}^{\infty}\left(g_{1}(x)+g_{2}(x)\right) f(x) d x \\ =\int_{-\infty}^{\infty} g_{1}(x) f(x) d x+\int_{-\infty}^{\infty} g_{2}(x) f(x) d x=E\left[g_{1}(x)\right]+E\left[g_{2}(x)\right], \\ E\left[g_{2}(x)\right]-E\left[g_{1}(x)\right]=\int_{-\infty}^{\infty}\left[g_{2}(x)-g_{1}(x)\right] f(x) d x \geq 0 . \end{gather}\]
Equation (2.19) follows from (2.18) , applied first with \(g_{1}(x)=g(x)\) and \(g_{2}(x)=|g(x)|\) and then with \(g_{1}(x)=-|g(x)|\) and \(g_{2}(x)=g(x)\) .
Example 2B . To illustrate the use of (2.15) to (2.19) , we note that \(E[4]=4, E\left[x^{2}-4 x\right]=E\left[x^{2}\right]-4 E[x]\) , and \(E\left[(x-2)^{2}\right]=E\left[x^{2}-4 x+4\right]\) \(=E\left[x^{2}\right]-4 E[x]+4\) .
We next derive an extremely important expression for the variance of a probability law:
\[\sigma^{2}=E\left[(x-E[x])^{2}\right]=E\left[x^{2}\right]-E^{2}[x]. \tag{2.20}\]
In words, the variance of a probability law is equal to its mean square, minus its square mean . To prove (2.20) , we write, letting \(m=E[x]\) ,
\begin{align} \sigma^{2} & =E\left[x^{2}-2 m x+m^{2}\right]=E\left[x^{2}\right]-2 m E[x]+m^{2} \\ & =E\left[x^{2}\right]-2 m^{2}+m^{2}=E\left[x^{2}\right]-m^{2}. \end{align}
In the remainder of this section we compute the mean and variance of various probability laws. A tabulation of the results obtained is given in Tables 3A and 3B at the end section 3.
Example 2C . The Bernoulli probability law with parameter \(p\) , in which \(0 \leq p \leq 1\) , is specified by the probability mass function \(p(\cdot)\) , given by \(p(0)=1-p, p(1)=p, p(x)=0\) for \(x \neq 0\) or 1. Its mean, mean square, and variance, letting \(q=1-p\) , are given by \begin{align} E[x] & =0 \cdot q+1 \cdot p=p \\ E\left[x^{2}\right] & =0^{2} \cdot q+1^{2} \cdot p=p \tag{2.21} \\ \sigma^{2} & =E\left[x^{2}\right]-m^{2}=p-p^{2}=p q . \end{align}
Example 2D . The binomial probability law with parameters \(n\) and \(p\) is specified by the probability mass function given by (4.5) of Chapter 4. Its mean is given by \begin{align} E[x] & =\sum_{k=0}^{n} k p(k)=\sum_{k=0}^{n} k\left(\begin{array}{l} n \\ k \end{array}\right) p^{k} q^{n-k} \tag{2.22} \\ & =n p \sum_{k=1}^{n}\left(\begin{array}{l} n-1 \\ k-1 \end{array}\right) p^{k-1} q^{(n-1)-(k-1)}=n p(p+q)^{n-1}=n p . \end{align}
Its mean square is given by
\[E\left[x^{2}\right]=\sum_{k=0}^{n} k^{2}\left(\begin{array}{l} n \tag{2.23} \\ k \end{array}\right) p^{z k} q^{n-k}.\]
To evaluate \(E\left[x^{2}\right]\) , we write \(k^{2}=k(k-1)+k\) . Then
\[E\left[x^{2}\right]=\sum_{k=2}^{n} k(k-1)\left(\begin{array}{l} n \tag{2.24} \\ k \end{array}\right) p^{k} q^{n-k}+E[x].\]
Since \(k(k-1)\left(\begin{array}{l}n \\ k\end{array}\right)=n(n-1)\left(\begin{array}{l}n-2 \\ k-2\end{array}\right)\) , the sum in (2.24) is equal to
\[n(n-1) p^{2} \sum_{k=2}^{n}\left(\begin{array}{l} n-2 \\ k-2 \end{array}\right) p^{k-2} q^{(n-2)-(k-2)}=n(n-1) p^{2}(p+q)^{n-2}.\]
Consequently, \(E\left[x^{2}\right]=n(n-1) p^{2}+n p\) , so that
\[E\left[x^{2}\right]=n p q+n^{2} p^{2}, \quad \sigma^{2}=E\left[x^{2}\right]-E^{2}[x]=n p q. \tag{2.25}\]
Example 2E . The hypergeometric probability law with parameters \(N, n\) , and \(p\) is specified by the probability mass function \(p(\cdot)\) given by (4.8) of Chapter 4. Its mean is given by \begin{align} E[x]=\sum_{k=0}^{n} k p(k) & =\frac{1}{\left(\begin{array}{c} N \\ n \end{array}\right)} \sum_{k=1}^{n} k\left(\begin{array}{c} N p \\ k \end{array}\right)\left(\begin{array}{c} N q \\ n-k \end{array}\right) \tag{2.26} \\ & =\frac{N p}{\left(\begin{array}{c} N \\ n \end{array}\right)} \sum_{k=1}^{n}\left(\begin{array}{l} a-1 \\ k-1 \end{array}\right)\left(\begin{array}{c} b \\ n-k \end{array}\right), \end{align} in which we have let \(a=N p, b=N q\) . Now, letting \(j=k-1\) and using (2.37) of Chapter 4, the last sum written is equal to \[\sum_{j=0}^{n-1}\left(\begin{array}{c} a-1 \\ j \end{array}\right)\left(\begin{array}{c} b \\ n-1-j \end{array}\right)=\left(\begin{array}{c} a+b-1 \\ n-1 \end{array}\right)=\left(\begin{array}{c} N-1 \\ n-1 \end{array}\right) \text {. }\] Consequently, \[E[x]=N p \frac{\left(\begin{array}{l} N-1 \tag{2.27} \\ n-1 \end{array}\right)}{\left(\begin{array}{l} N \\ n \end{array}\right)}=n p.\] Next, we evaluate \(E\left[x^{2}\right]\) by first evaluating \(E[x(x-1)]\) and then using the fact that \(E\left[x^{2}\right]=E[x(x-1)]+E[x]\) . Now
\begin{align} \left(\begin{array}{l} N \\ n \end{array}\right) E[x(x-1)] & =\sum_{k=2}^{n} k(k-1)\left(\begin{array}{l} a \\ k \end{array}\right) \left(\begin{array}{c} b \\ n-k \end{array}\right) \\ & =a(a-1) \sum_{k=2}^{n} \left(\begin{array}{l} a-2 \\ k-2 \end{array}\right) \left(\begin{array}{c} b \\ n-k \end{array}\right) \\ & =a(a-1)\left(\begin{array}{c} a+b-2 \\ n-2 \end{array}\right) \\ & =N p(N p-1)\left(\begin{array}{c} N-2 \\ n-2\end{array}\right) \tag{2.28} \end{align}
\begin{align} E\left[x^{2}\right] & =n p(N p-1) \frac{n-1}{N-1}+n p=\frac{n p}{N-1}(N p(n-1)+N-n) \\ \sigma^{2} & =\frac{n p}{N-1}(N-n+p N(n-1)-p n(N-1))=n p q \frac{N-n}{N-1} \text {. } \end{align}
Notice that the mean of the hypergeometric probability law is the same as that of the corresponding binomial probability law, whereas the variances differ by a factor that is approximately equal to 1 if the ratio \(n / N\) is a small number.
Example 2F . The uniform probability law over the interval \(a\) to \(b\) has probability density function \(f(\cdot)\) given by (4.10) of Chapter 4. Its mean, mean square, and variance are given by
\begin{align} E[x] & =\int_{-\infty}^{\infty} x f(x) d x=\frac{1}{b-a} \int_{a}^{b} x d x=\frac{b^{2}-a^{2}}{2(b-a)}=\frac{b+a}{2} \\ E\left[x^{2}\right] & =\int_{-\infty}^{\infty} x^{2} f(x) d x=\frac{1}{b-a} \int_{a}^{b} x^{2} d x=\frac{1}{3}\left(b^{2}+b a+a^{2}\right) \\ \sigma^{2} & =E\left[x^{2}\right]-E^{2}[x]=\frac{1}{12}(b-a)^{2} . \end{align}
Note that the variance of the uniform probability law depends only on the length of the interval, whereas the mean is equal to the mid-point of the interval. The higher moments of the uniform probability law are also easily obtained:
\[E\left[x^{n}\right]=\frac{1}{b-a} \int_{a}^{b} x^{n} d x=\frac{b^{n+1}-a^{n+1}}{(n+1)(b-a)}. \tag{2.30}\]
Example 2G . The Cauchy probability law with parameters \(\alpha=0\) and \(\beta=1\) is specified by the probability density function
\[f(x)=\frac{1}{\pi} \frac{1}{1+x^{2}}. \tag{2.31}\]
The mean \(E[x]\) of the Cauchy probability law does not exist, since
\[E[|x|]=\frac{1}{\pi} \int_{-\infty}^{\infty}|x| \frac{1}{1+x^{2}} d x=\infty. \tag{2.32}\]
However, for \(r<1\) the \(r\) th absolute moments
\[E\left[|x|^{r}\right]=\frac{1}{\pi} \int_{-\infty}^{\infty}|x|^{r} \frac{1}{1+x^{2}} dx \tag{2.33}\]
do exist, as one may see by applying theoretical exercise 2.1.
Theoretical Exercises
2.1 . Test for convergence or divergence of infinite series and improper integrals . Prove the following statements. Let \(h(x)\) be a continuous function. If, for some real number \(r>1\) , the limits
\[\lim _{x \rightarrow \infty} x^{r}|h(x)|, \quad \lim _{x \rightarrow-\infty}|x|^{r}|h(x)| \tag{2.34}\]
both exist and are finite, then
\[\int_{-\infty}^{\infty} h(x) d x, \quad \sum_{k=-\infty}^{\infty} h(k) \tag{2.35}\]
converge absolutely; if, for some \(r \leq 1\) , either of the limits in (2.34) exist and is not equal to 0, then the expressions in (2.35) fail to converge absolutely.
2.2 . Pareto’s distribution with parameters \(r\) and \(A\) , in which \(r\) and \(A\) are positive, is defined by the probability density function
\begin{align} f(x) = \begin{cases} r A^{r} \frac{1}{x^{r+1}}, & \text{for } x \geq A \\[2mm] 0, & \text{for } x < A. \end{cases} \tag{2.36} \end{align}
Show that Pareto’s distribution possesses a finite \(n\) th moment if and only if \(n
2.3 . “Student’s” \(t\) -distribution with parameter \(\nu>0\) is defined as the continuous probability law specified by the probability density function
\[f(x)=\frac{1}{\sqrt{v \pi}} \frac{\Gamma[(\nu+1) / 2]}{\Gamma(v / 2)}\left(1+\frac{x^{2}}{v}\right)^{-(\nu+1) / 2} \tag{2.37}\]
Note that “Student’s” \(t\) -distribution with parameter \(v=1\) coincides with the Cauchy probability law given by (2.31). Show that for “Student’s” \(t\) -distribution with parameter \(v\) (i) the \(n\) th moment \(E\left[x^{n}\right]\) exists only for \(n<\nu\) , (ii) if \(n<\nu\) and \(n\) is odd, then \(E\left[x^{n}\right]=0\) , (iii) if \(n<\nu\) and \(n\) is even, then
\[E\left[x^{n}\right]=y^{n / 2} \frac{\Gamma[(n+1) / 2] \Gamma[(\nu-n) / 2]}{\Gamma(1 / 2) \Gamma(\nu / 2)} \tag{2.38}\]
2.4 . A characterization of the mean . Consider a probability law with finite mean \(m\) . Define, for every real number \(a, h(a)=E\left[(x-a)^{2}\right]\) . Show that \(h(a)=E\left[(x-m)^{2}\right]+(m-a)^{2}\) . Consequently \(h(a)\) is minimized at \(a=m\) , and its minimum value is the variance of the probability law.
2.5 . A geometrical interpretation of the mean of a probability law . Show that for a continuous probability law with probability density function \(f(\cdot)\) and distribution function \(F(\cdot)\)
\begin{align} & \int_{0}^{\infty}[1-F(x)] d x=\int_{0}^{\infty} d x \int_{x}^{\infty} d y f(y)=\int_{0}^{\infty} y f(y) d y, \\ - & \int_{-\infty}^{0} F(x) d x=-\int_{-\infty}^{0} d x \int_{-\infty}^{x} d y f(y)=-\int_{0}^{-\infty} y f(y) d y . \tag{2.39} \end{align}
Consequently the mean \(m\) of the probability law may be written
\[m=\int_{-\infty}^{\infty} y f(y) d y=\int_{0}^{\infty}[1-F(x)] d x-\int_{-\infty}^{0} F(x) dx. \tag{2.40}\]
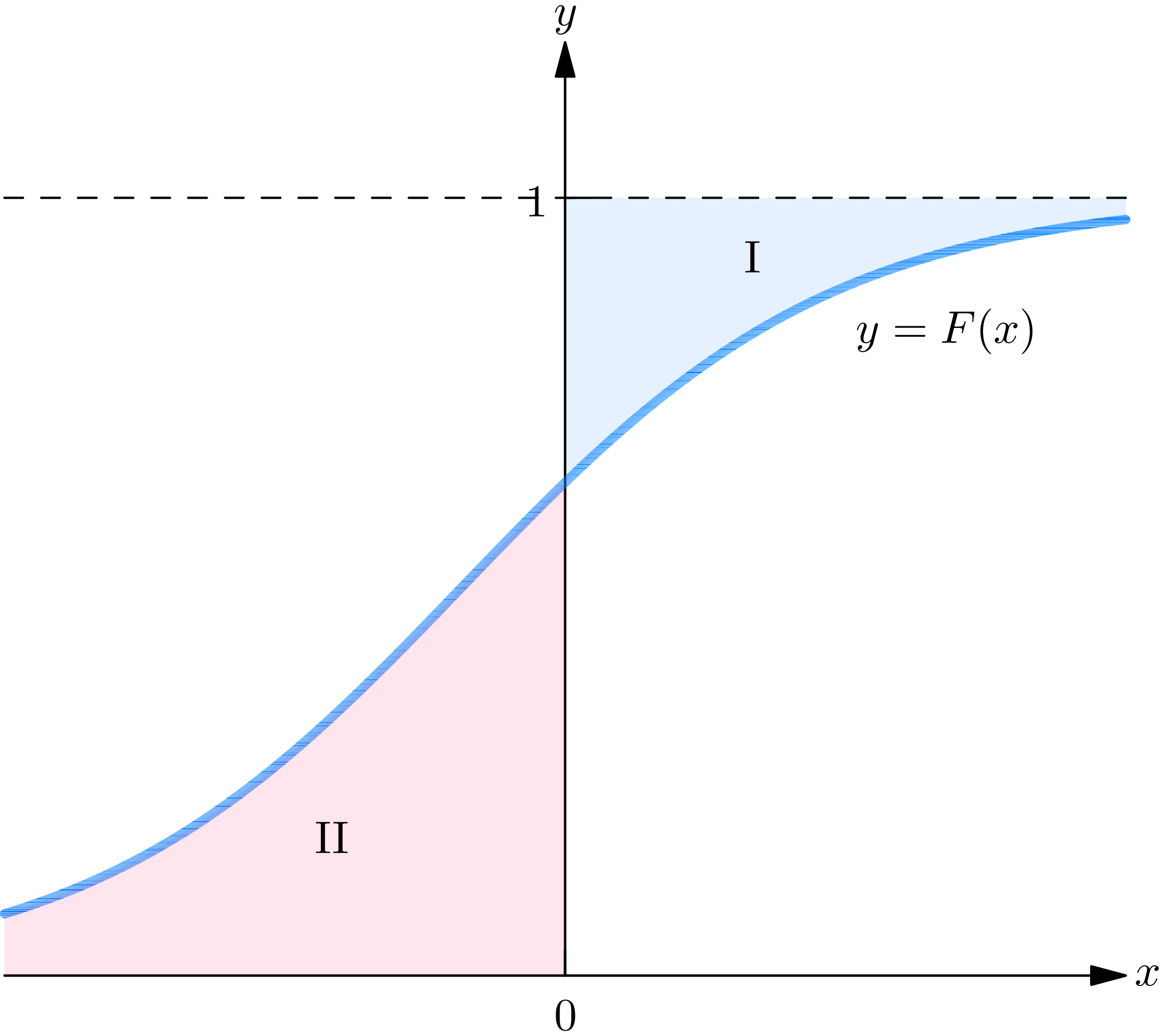
These equations may be interpreted geometrically. Plot the graph \(y=F(x)\) of the distribution function on an \((x, y)\) -plane, as in Fig. 2A, and define the areas I and II as indicated: \(\mathrm{I}\) is the area to the right of the \(y\) -axis bounded by \(y=1\) and \(y=F(x)\) ; II is the area to the left of the \(y\) -axis bounded by \(y=0\) and \(y=F(x)\) . Then the mean \(m\) is equal to area I, minus area II. Although we have proved this assertion only for the case of a continuous probability law, it holds for any probability law.
2.6 . A geometrical interpretation of the higher moments . Show that the \(n\) th moment \(E\left[x^{n}\right]\) of a continuous probability law with distribution function \(F(\cdot)\) can be expressed for \(n=1,2, \ldots\)
\[E\left[x^{n}\right]=\int_{-\infty}^{\infty} x^{n} f(x)\ d x=\int_{0}^{\infty} dy\ n y^{n-1}\left[1-F(y)+(-1)^{n} F(-y)\right]. \tag{2.41}\]
Use (2.41) to interpret the \(n\) th moment in terms of area.
2.7 . The relation between the moments and central moments of a probability law . Show that from a knowledge of the moments of a probability law one may obtain a knowledge of the central moments, and conversely. In particular, it is useful to have expressions for the first 4 central moments in terms of the moments. Show that
\begin{align} & E\left[(x-E[x])^{3}\right]=E\left[x^{3}\right]-3 E[x] E\left[x^{2}\right]+2 E^{3}[x] \\ & E\left[(x-E[x])^{4}\right]=E\left[x^{4}\right]-4 E[x] E\left[x^{3}\right]+6 E^{2}[x] E\left[x^{2}\right]-3 E^{4}[x]. \tag{2.42} \end{align}
2.8 . The square mean is less than or equal to the mean square . Show that
\[|E[x]| \leq E[|x|] \leq E^{1 / 2}\left[x^{2}\right]. \tag{2.43}\]
Give an example of a probability law whose mean square \(E\left[x^{2}\right]\) is equal to its square mean.
2.9 . The mean is not necessarily greater than or equal to the variance . The binomial and the Poisson are probability laws having the property that their mean \(m\) is greater than or equal to their variance \(\sigma^{2}\) (show this); this circumstance has sometimes led to the belief that for the probability law of a random variable assuming only nonnegative values it is always true that \(m \geq \sigma^{2}\) . Prove this is not the case by showing that \(m<\sigma^{2}\) for the probability law of the number of failures up to the first success in a sequence of independent repeated Bernoulli trials.
2.10 . The median of a probability law . The mean of a probability law provides a measure of the “mid-point” of a probability distribution. Another such measure is provided by the median of a probability law , denoted by \(m_{e}\) , which is defined as a number such that
\[\lim _{x \rightarrow m_{e}^{-}} F(x)=F\left(m_{e}-0\right) \leq \frac{1}{2} \leq F\left(m_{e}+0\right)=\lim _{x \rightarrow m_{e}^{+}} F(x). \tag{2.44}\]
If the probability law is continuous, the median \(m_{e}\) may be defined as a number satisfying \(\displaystyle \int_{-\infty}^{m_{e}} f(x) d x=\frac{1}{2}\) . Thus \(m_{e}\) is the projection on the \(x\) -axis of the point in the \((x, y)\) -plane at which the line \(y=\frac{1}{2}\) intersects the curve \(y=F(x)\) . A more probabilistic definition of the median \(m_{e}\) is as a number such that \(P\left[X
\[E[|x-a|]=E\left[\left|x-m_{e}\right|\right]+2 \int_{a}^{m_{e}}(x-a) f(x) dx. \tag{2.45}\]
2.11 . The mode of a continuous or discrete probability law . For a continuous probability law with probability density function \(f(x)\) a mode of the probability law is defined as a number \(m_{0}\) at which the probability density has a relative maximum; assuming that the probability density function is twice differentiable, a point \(m_{0}\) is a mode if \(f^{\prime}\left(m_{0}\right)=0\) and \(f^{\prime \prime}\left(m_{0}\right)<0\) . Since the probability density function is the derivative of the distribution function \(F(\cdot)\) , these conditions may be stated in terms of the distribution function: a point \(m_{0}\) is a mode if \(F^{\prime \prime}\left(m_{0}\right)=0\) and \(F^{\prime \prime \prime}\left(m_{0}\right)<0\) . Similarly, for a discrete probability law with probability mass function \(p(\cdot)\) a mode of the probability law is defined as a number \(m_{0}\) at which the probability mass function has a relative maximum; more precisely, \(p\left(m_{0}\right) \geq p(x)\) for \(x\) equal to the largest probability mass point less than \(m_{0}\) and for \(x\) equal to the smallest probability mass point larger than \(m_{0}\) . A probability law is said to be (i) unimodal if it possesses just 1 mode, (ii) bimodal if it possesses exactly 2 modes, and so on. Give examples of continuous and discrete probability laws which are (a) unimodal, (b) bimodal. Give examples of continuous and discrete probability laws for which the mean, median, and mode ( \(c\) ) coincide, \((d)\) are all different.
2.12 . The interquartile range of a probability law . Possible measures exist of the dispersion of a probability distribution, in addition to the variance, which one may consider (especially if the variance is infinite). The most important of these is the interquartile range of the probability law, defined as follows: for any number \(p\) , between 0 and 1, define the \(p\) percentile \(\mu(p)\) of the probability law as the number satisfying \(F(\mu(p)-0) \leq p \leq\) \(F(\mu(p)+0)\) . Thus \(\mu(p)\) is the projection on the \(x\) -axis of the point in the \((x, y)\) -plane at which the line \(y=p\) intersects the curve \(y=F(x)\) . The 0.5 percentile is usually called the median. The interquartile range, defined as the difference \(\mu(0.75)-\mu(0.25)\) , may be taken as a measure of the dispersion of the probability law.
(i) Show that the ratio of the interquartile range to the standard deviation is (a), for the normal probability law with parameters \(m\) and \(\sigma, 1.3490\) , (b), for the exponential probability law with parameter \(\lambda, \log _{e} 3=1.099\) , (c), for the uniform probability law over the interval \(a\) to \(b, \sqrt{3}\) .
(ii) Show that the Cauchy probability law specified by the probability density function \(f(x)=\left[\pi\left(1+x^{2}\right)\right]^{-1}\) possesses neither a mean nor a variance. However, it possesses a median and an interquartile range given by \(m_{e}=\mu\left(\frac{1}{2}\right)=0, \mu\left(\frac{3}{4}\right)-\mu\left(\frac{1}{4}\right)=2\) .
Exercises
In exercises 2.1 to 2.7, compute the mean and variance of the probability law specified by the probability density function, probability mass function, or distribution function given.
2.1 . \begin{align} & \text{(i)} \quad f(x) = \begin{cases} 2x, & \text{for } 0 < x < 1 \\[2mm] 0, & \text{otherwise.} \end{cases} \\[3mm] & \text{(ii)} \quad f(x) = \begin{cases} |x|, & \text{for } |x| \leq 1, \\[2mm] 0, & \text{otherwise.} \end{cases} \\[3mm] & \text{(iii)} \quad f(x) = \begin{cases} \frac{1 + 0.8x}{2}, & \text{for } |x| < 1, \\[2mm] 0, & \text{otherwise.} \end{cases} \end{align}
Answer
Mean (i) \(\frac{2}{3}\) , (ii) 0 , (iii) \(\frac{4}{15}\) ; variance (i) \(\frac{1}{28}\) , (ii) \(\frac{1}{2}\) , (iii) \(\frac{59}{2} \frac{9}{2}\) .
2.2 . \begin{align} & \text{(i)} \quad f(x) = \begin{cases} 1 - |1 - x|, & \text{for } 0 < x < 1 \\[2mm] 0, & \text{otherwise.} \end{cases} \\[3mm] & \text{(ii)} \quad f(x) = \begin{cases} \frac{1}{2 \sqrt{x}}, & \text{for } 0 < x < 1 \\[2mm] 0, & \text{otherwise.} \end{cases} \end{align}
2.3 . \begin{align} \text{(i)} \quad f(x) & = \frac{1}{\pi \sqrt{3}}\left(1+\frac{x^2}{3}\right)^{-1} \\[3mm] \text{(ii)} \quad f(x) & = \frac{2}{\pi \sqrt{3}}\left(1+\frac{x^2}{3}\right)^{-2} \\[3mm] \text{(iii)} \quad f(x) & = \frac{8/3}{\pi \sqrt{3}}\left(1+\frac{x^2}{3}\right)^{-3} \end{align}
Answer
Mean (i) does not exist, (ii) 0, (iii) 0; variance (i) does not exist, (ii) 3, (iii) 1.
2.4 . \begin{align} & \text{(i)} \quad f(x) = \frac{1}{2 \sqrt{2 \pi}} e^{-\frac{1}{2}\left(\frac{x-2}{2}\right)^{2}} \\[3mm] & \text{(ii)} \quad f(x) = \begin{cases} \sqrt{\frac{2}{\pi}} e^{-\frac{1}{2} x^2}, & \text{for } x > 0 \\[2mm] 0, & \text{elsewhere.} \end{cases} \end{align}
2.5 . \begin{align} & \text{(i)} \quad p(x) = \begin{cases} \frac{1}{3}, & \text{for } x = 0 \\[2mm] \frac{2}{3}, & \text{for } x = 1, \\[2mm] 0, & \text{elsewhere.} \end{cases} \\[3mm] & \text{(ii)} \quad p(x) = \begin{cases} \displaystyle \binom{6}{x} \left(\frac{2}{3}\right)^x \left(\frac{1}{3}\right)^{6-x}, & \text{for } x = 0, 1, \ldots, 6 \\[2mm] 0, & \text{elsewhere.} \end{cases} \\[3mm] & \text{(iii)} \quad p(x) = \begin{cases} \frac{\displaystyle\binom{8}{x} \binom{4}{6-x}}{\displaystyle \binom{12}{6}}, & \text{for } x = 0, 1, \ldots, 6 \\[2mm] 0, & \text{elsewhere.} \end{cases} \end{align}
Answer
Mean (i) \(\frac{2}{3}\) , (ii) 4 (iii) 4; variance (i) \(\frac{2}{8}\) , (ii) \(\frac{4}{3}\) , (iii) \(\frac{8}{1 \frac{1}{4}}\) .
2.6 . \begin{align} & \text{(i)} \quad p(x) = \begin{cases} \frac{2}{3} \left(\frac{1}{3}\right)^{x-1}, & \text{for } x = 1, 2, \ldots \\[2mm] 0, & \text{otherwise.} \end{cases} \\[3mm] & \text{(ii)} \quad p(x) = \begin{cases} e^{-2} \frac{2^x}{x!}, & \text{for } x = 0, 1, 2, \ldots \\[2mm] 0, & \text{otherwise.} \end{cases} \end{align}
2.7 . \begin{align} & \text{(i)} \quad F(x) = \begin{cases} 0, & \text{for } x < 0 \\[2mm] x^2, & \text{for } 0 \leq x \leq 1 \\[2mm] 1, & \text{for } x > 1. \end{cases} \\[3mm] & \text{(ii)} \quad F(x) = \begin{cases} 0, & \text{for } x < 0 \\[2mm] x^{1/2}, & \text{for } 0 \leq x \leq 1 \\[2mm] 1, & \text{for } x > 1. \end{cases} \end{align}
Answer
Mean (i) \(\frac{2}{3}\) , (ii) \(\frac{1}{3}\) ; variance (i) \(\frac{1}{2}\) , (ii) \(\frac{4}{45}\) .
2.8 . Compute the means and variances of the probability laws obeyed by the numerical valued random phenomena described in exercise 4.1 of Chapter 4.
2.9 . For what values of \(r\) does the probability law, specified by the following probability density function, possess (i) a finite mean, (ii) a finite variance:
\begin{align} f(x) = \begin{cases} \frac{r-1}{2|x|^{r}}, & \text{for } |x| > 1 \\[2mm] 0, & \text{otherwise.} \end{cases} \end{align}
Answer
(i) \(r>2\) ; (ii) \(r>3\) .
- For the benefit of the reader acquainted with the theory of Lebesgue integration, let it be remarked that if the integral in (2.3) is defined as an integral in the sense of Lebesgue then the notion of expectation \(E[g(x)]\) may be defined for a Borel function \(g(x)\) . ↩︎