Consider the probability function \(P[\cdot]\) of a numerical-valued random phenomenon. The question arises concerning the convenient ways of stating the function without having actually to state the value of \(P[E]\) for every set of real numbers \(E\) . In general, to state the function \(P[\cdot]\) , as with any function, one has to enumerate all the members of the domain of the function \(P[\cdot]\) , and for each of these members of the domain one states the value of the function. In special circumstances (which fortunately cover most of the cases encountered in practice) more convenient methods are available.
For many probability functions there exists a function \(f(\cdot)\) , defined for all real numbers \(x\) , from which \(P[E]\) can, for any event \(E\) , be obtained by integration: \[P[E]=\int_{E} f(x) dx. \tag{2.1}\]
Given a probability function \(P[\cdot]\) , which may be represented in the form of (2.1) in terms of some function \(f(\cdot)\) , we call the function \(f(\cdot)\) the probability density function of the probability function \(P[\cdot]\) , and we say that the probability function \(P[\cdot]\) is specified by the probability density function \(f(\cdot)\) .
A function \(f(\cdot)\) must have certain properties in order to be a probability density function. To begin with, it must be sufficiently well behaved as a function so that the integral 1 in (2.1) is well defined. Next, letting \(E=R\) in (2.1) , \[1=P[R]=\int_{R} f(x) d x=\int_{-\infty}^{\infty} f(x) dx. \tag{2.2}\]
It is necessary that \(f(\cdot)\) satisfy (2.2) ; in words, the integral of \(f(\cdot)\) from \(-\infty\) to \(\infty\) must be equal to 1.
A function \(f(\cdot)\) is said to be a probability density function if it satisfies (2.2) and, in addition, 2 satisfies the condition \[f(x) \geq 0 \quad \text { for all } x \text { in } R, \tag{2.3}\] since a function \(f(\cdot)\) satisfying (2.2) and (2.3) is the probability density function of a unique probability function \(P[\cdot]\) , namely the probability function with value \(P[E]\) at any event \(E\) given by (2.1) .
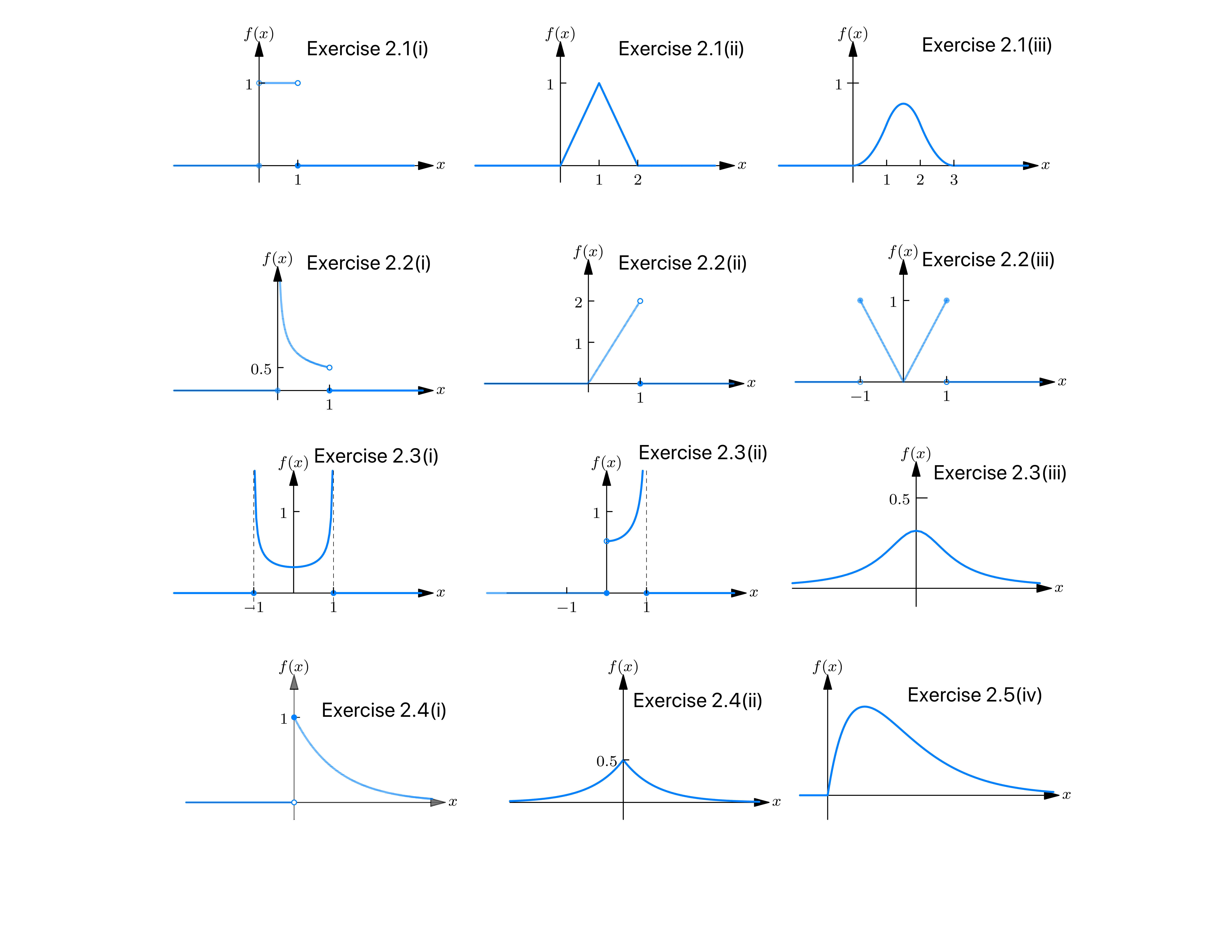
Some typical probability density functions are illustrated in Fig.2A .
Example 2A . Verifying that a function is a probability density function . Suppose one is told that the time one has to wait for a bus on a certain street corner is a numerical-valued random phenomenon, with a probability function, specified by the probability density function \(f(\cdot)\) , given by \begin{align} f(x) & = \begin{cases} 4x - 2x^{2} - 1, & \text{if } 0 \leq x \leq 2 \tag{2.4} \\ 0, & \text{otherwise}. \end{cases} \end{align}
The function \(f(\cdot)\) is negative for various values of \(x\) ; in particular, it is negative for \(0 \leq x \leq \frac{1}{4}\) (prove this statement). Consequently, it is not possible for \(f(\cdot)\) to be a probability density function. Next, suppose that the probability density function \(f(\cdot)\) is given by \begin{align} f(x) & = \begin{cases} 4x - 2x^{2}, & \text{if } 0 \leq x \leq 2 \tag{2.5} \\ 0, & \text{otherwise}. \end{cases} \end{align}
The function \(f(\cdot)\) , given by (2.5) , is nonnegative (prove this statement). However, its integral from \(-\infty\) to \(\infty\) , \[\int_{-\infty}^{\infty} f(x) d x=\frac{8}{3},\] is not equal to 1. Consequently the function \(f(\cdot)\) , given by (2.5) is not a probability density function. However, the function \(f(\cdot)\) , given by \begin{align} f(x) & = \begin{cases} \frac{3}{8}\left(4x - 2x^{2}\right), & \text{if } 0 \leq x \leq 2 \\ 0, & \text{otherwise}. \end{cases} \end{align} is a probability density function.
Example 2B . Computing probabilities from a probability density function . Let us consider again the numerical-valued random phenomenon, discussed in example 1A , that consists in observing the time one has to wait for a bus at a certain bus stop. Let us assume that the probability function \(P[\cdot]\) of this phenomenon may be expressed by (2.1) in terms of the function \(f(\cdot)\) , whose graph is sketched in Fig. 2B . An algebraic formula for \(f(\cdot)\) can be written as follows: \begin{align} f(x) =\begin{cases} 0, & \text { for } x<0 \tag{2.6} \\[2mm] \left(\frac{1}{9}\right)(x+1), & \text { for } 0 \leq x < 1 \\[2mm] \left(\frac{4}{9}\right)\left(x-\left(\frac{1}{2}\right)\right), & \text { for } 1 \leq x<\left(\frac{3}{2}\right) \\[2mm] \left(\frac{4}{9}\right)\left(\left(\frac{5}{2}\right)-x\right), & \text { for }\left(\frac{3}{2}\right) \leq x<2 \\[2mm] \left(\frac{1}{9}\right)(4-x), & \text { for } 2 \leq x<3 \\[2mm] \left(\frac{1}{9}\right), & \text { for } 3 \leq x<6 \\[2mm] 0 & \text { for } 6 \leq x \end{cases} \end{align}
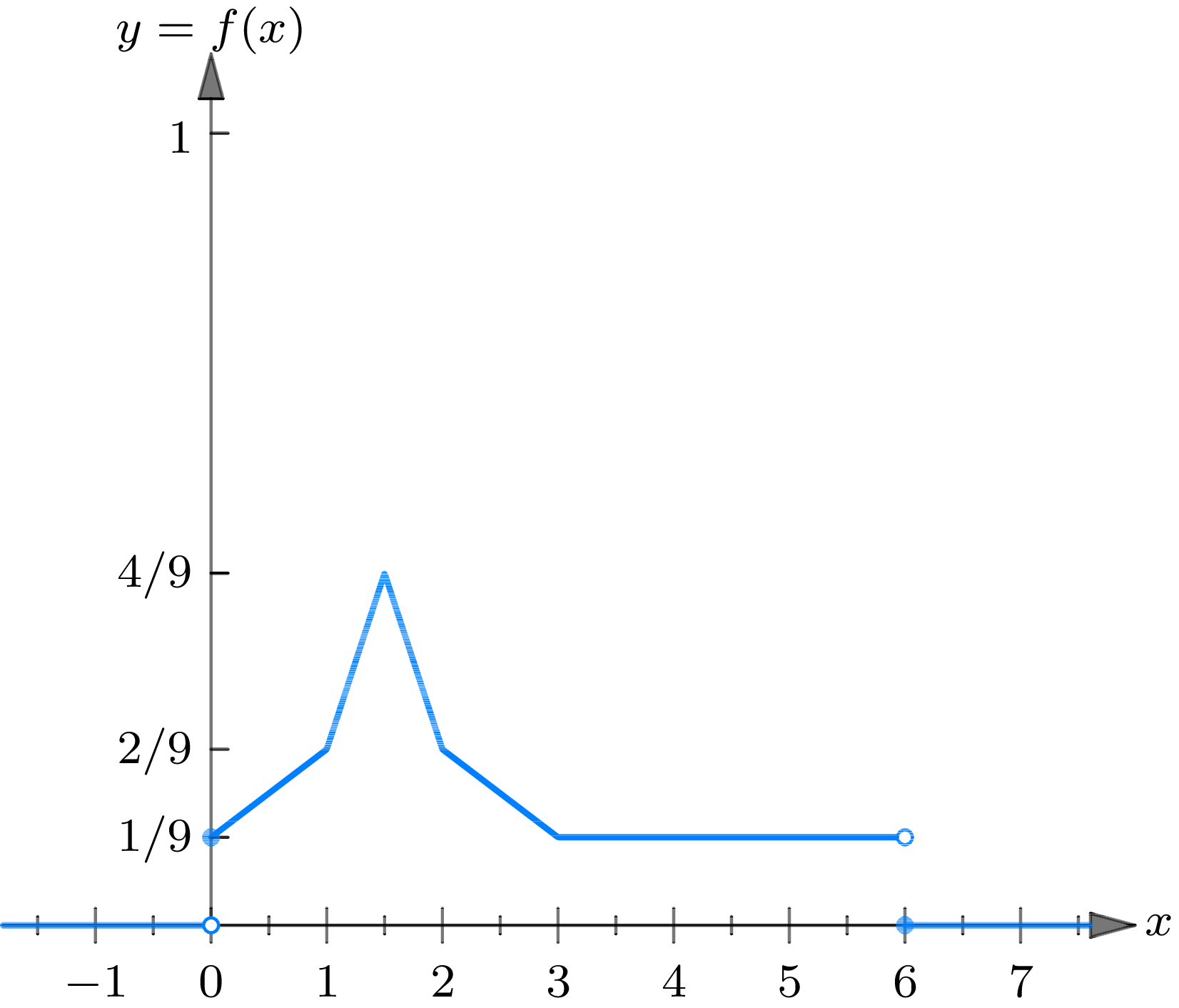
From (2.1) it follows that if \(A=\{x: 0 \leq x \leq 2\}\) and \(B=\{x: 1 \leq x \leq 3\}\) then \[\begin{gather} P[A]=\int_{0}^{2} f(x) d x=\frac{1}{2}, \quad P[B]=\int_{1}^{3} f(x) d x=\frac{1}{2}, \\ P[A B]=\int_{1}^{2} f(x) d x=\frac{1}{3}, \end{gather}\] which agree with the values assumed in example 1A .
Example 2C . The lifetime of a vacuum tube. Consider the numerical valued random phenomenon that consists in observing the total time a vacuum tube will burn from the moment it is first put into service. Suppose that the probability function \(P\left[\cdot\right]\) of this phenomenon is expressed by (2.1) in terms of the function \(f(\cdot)\) given by \begin{align} f(x) = \begin{cases} 0, & \text{for } x < 0 \\[2mm] \frac{1}{1000} e^{-\frac{x}{1000}}, & \text{for } x \geq 0. \end{cases} \end{align}
Let \(E\) be the event that the tube burns between 100 and 1000 hours, inclusive, and let \(F\) be the event that the tube burns more than 1000 hours. The events \(E\) and \(F\) may be represented as subsets of the real line: \(E=\) \(\{x: 100 \leq x \leq 1000\}\) and \(F=\{x: 1000<x\}\) . The probabilities of \(E\) and \(F\) are given by \begin{align} P[E] & = \int_{100}^{1000} f(x) dx = \frac{1}{1000} \int_{100}^{1000} e^{-(x / 1000)} dx \\[2mm] & = -e^{-(x / 1000)}\mid_{100}^{1000} = e^{-0.1}-e^{-1}=0.537. \\[2mm] P[F] & =\int_{1000}^{\infty} f(x) d x =\frac{1}{1000} \int_{1000}^{\infty} e^{-(x / 1000)} dx \\[2mm] & =-\left.e^{-(x / 1000)}\right|_{1000} ^{\infty} =e^{-1}=0.368. \end{align}
For many probability functions there exists a function \(p(\cdot)\) , defined for all real numbers \(x\) , but with value \(p(x)\) equal to 0 for all \(x\) except for a finite or countably infinite set of values of \(x\) at which \(p(x)\) is positive, such that from \(p(\cdot)\) the value of \(P[E]\) can be obtained for any event \(E\) by summation: \[P[E]=\sum_{\substack{\text { over all } \\ \text { points } x \text { in } E \\ \text { such that } p(x)>0}} p(x) \tag{2.7}\] In order that the sum in (2.7) may be meaningful, it suffices to impose the condition [letting \(E=R\) in (2.7) ] that \[1=\sum_{\substack{\text { over all } \\ \text { points } x \text { in } \\ \text { such that } p(x)>0}} p(x) \tag{2.8}\]
Given a probability function \(P[\cdot]\) , which may be represented in the form (2.7) , we call the function \(p(\cdot)\) the probability mass function of the probability function \(P[\cdot]\) , and we say that the probability function \(P[\cdot]\) is specified by the probability mass function \(p(\cdot)\) .
A function \(p(\cdot)\) , defined for all real numbers, is said to be a probability mass function if (i) \(p(x)\) equals zero for all \(x\) , except for a finite or countably infinite set of values of \(x\) for which \(p(x)>0\) , and (ii) the infinite series in (2.8) converges and sums to 1. Such a function is the probability mass function of a unique probability function \(P[\cdot]\) defined on the subsets of the real line, namely the probability function with value \(P[E]\) at any set \(E\) given by (2.7) .
Example 2D . Computing probabilities from a probability mass function . Let us consider again the numerical-valued random phenomenon considered in examples 1A and 2B. Let us assume that the probability function \(P[\cdot]\) of this phenomenon may be expressed by (2.7) in terms of the function \(p(\cdot)\) , whose graph is sketched in Fig. 2C .
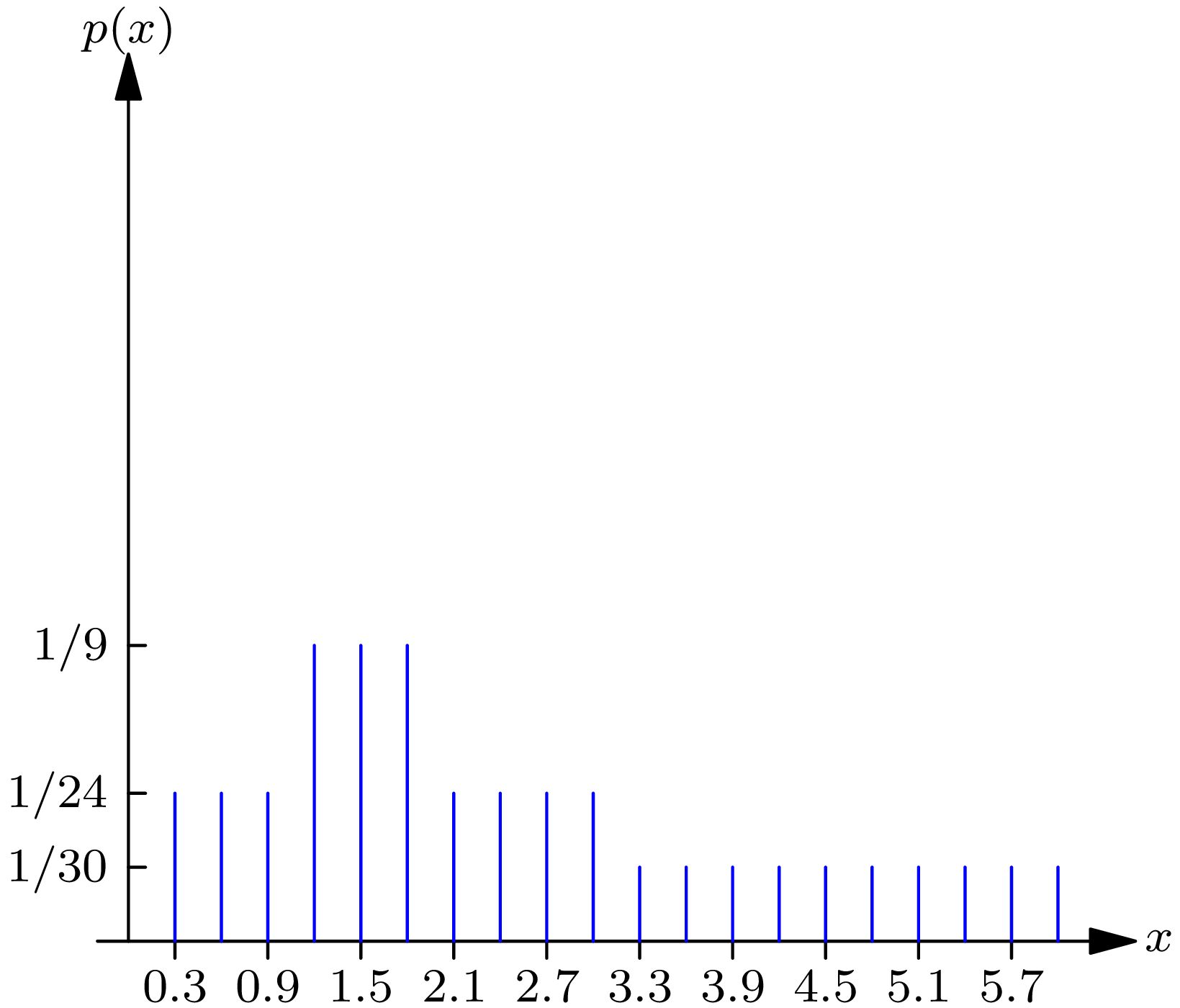
An algebraic formula for \(p(\cdot)\) can be written as follows: \begin{align} p(x) = \begin{cases} 0, & \text{unless } x = 0.3k \text{ for some } k = 0, 1, \ldots, 20 \\[2mm] \frac{1}{24}, & \text{for } x = 0, 0.3, 0.6, 0.9, 2.1, 2.4, 2.7, 3.0 \\[2mm] \frac{1}{9}, & \text{for } x = 1.2, 1.5, 1.8 \\[2mm] \frac{1}{30}, & \text{for } x = 3.3, 3.6, 3.9, 4.2, 4.5, 4.8, 5.1, 5.4, 5.7, 6.0 \end{cases} \end{align}
It then follows that \begin{align} P[A] & =p(0)+p(0.3)+p(0.6)+p(0.9)+p(1.2)+p(1.5)+p(1.8) \\ & =\frac{1}{2} \\ P[B] & =p(1.2)+p(1.5)+p(1.8)+p(2.1)+p(2.4)+p(2.7)+p(3.0) \\ & =\frac{1}{2} \\ P[A B] & =p(1.2)+p(1.5)+p(1.8)=\frac{1}{3} \end{align} which agree with the values assumed in example 1A .
The terminology of “density function” and “mass function” comes from the following physical representation of the probability function \(P[\cdot]\) of a numerical-valued random phenomenon. We imagine that a unit mass of some substance is distributed over the real line in such a way that the amount of mass over any set \(B\) of real numbers is equal to \(P[B]\) . The distribution of substance possesses a density, to be denoted by \(f(x)\) , at the point \(x\) , if for any interval containing the point \(x\) of length \(h\) (where \(h\) is a sufficiently small number) the mass of substance attached to the interval is equal to \(h f(x)\) . The distribution of substance possesses a mass, to be denoted by \(p(x)\) , at the point \(x\) , if there is a positive amount \(p(x)\) of substance concentrated at the point.
We shall see in section 3 that a probability function \(P[\cdot]\) always possesses a probability density function and a probability mass function. Consequently, in order for a probability function to be specified by either its probability density function or its probability mass function, it is necessary (and, from a practical point of view, sufficient) that one of these functions vanish identically.
Exercises
Verify that each of the functions \(f(\cdot)\) , given in exercises \(2.1-2.5\) , is a probability density function (by showing that it satisfies (2.1) and (2.3) ) and sketch its graph. 3 Hint : use freely the facts developed in the appendix to this section.
2.1. \begin{align} \text{(i)} \quad f(x) & =\begin{cases} 1, & \text{for }0<x<1 \\ 0, & \text{elsewhere.} \end{cases} \\ \\ \text{(ii)} \quad f(x) & =\begin{cases} 1-|1-x|, & \text{for }0<x<2 \\ 0, & \text{elsewhere.} \end{cases} \\ \\ \text{(iii)} \quad f(x) & =\begin{cases} \frac{1}{2}x^{2}, & \text{for }0< x \leq 1 \\[2mm] \frac{1}{2}(x^{2}-3(x-1)^{2}), & \text{for }1\le x<2 \\[2mm] \frac{1}{2}(x^{2}-3(x-1)^{2}+3(x-2)^{2}), & \text{for }2\le x\leq3 \\[2mm] 0, & \text{elsewhere.} \end{cases} \end{align}
2.2. \begin{align} \text{(i)} \quad f(x) & =\begin{cases} \frac{1}{2\sqrt{x}}, & \text{for }0<x<1 \\ 0, & \text{elsewhere.} \end{cases} \\ \\ \text{(ii)} \quad f(x) & =\begin{cases} 2x, & \text{for }0<x<1 \\ 0, & \text{elsewhere.} \end{cases} \\ \\ \text{(iii)} \quad f(x) & =\begin{cases} |x|, & \text{for }|x| \leq 1 \\ 0, & \text{elsewhere.} \end{cases} \end{align}
2.3. \begin{align} \text{(i)} \quad f(x) & =\begin{cases} \dfrac{1}{\pi \sqrt{1-x^{2}}}, & \text{for }|x|<1 \\ 0, & \text{elsewhere.} \end{cases} \\ \\ \text{(ii)} \quad f(x) & =\begin{cases} \dfrac{2}{\pi} \frac{1}{\sqrt{1-x^{2}}}, & \text{for }0<x<1 \\ 0, & \text{elsewhere.} \end{cases} \\ \\ \text{(iii)} \quad f(x) & = \frac{1}{\pi} \frac{1}{1+x^{2}} \\ \text{(iv)} \quad f(x) & =\frac{1}{\pi \sqrt{3}}\left(1+\frac{x^{2}}{3}\right)^{-1} \end{align}
2.4. \begin{align} \text{(i)} \quad f(x) & =\begin{cases} e^{-x}, & \text{for }x \geq 0 \\ 0, & x<0 \end{cases} \\ \\ \text{(ii)} \quad f(x) & =\left(\frac{1}{2}\right) e^{-|x|} \\ \text{(iii)} \quad f(x) & =\frac{e^{x}}{\left(1+e^{x}\right)^{2}} \\ \text{(iv)} \quad f(x) & =\frac{2}{\pi} \frac{e^{x}}{1+e^{2 x}} \end{align}
2.5. \begin{align} \text{(i)} \quad f(x) & =\frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2} x^{2}} \\ \text{(ii)} \quad f(x) & =\frac{1}{2 \sqrt{2 \pi}} e^{-\frac{1}{2}\left(\frac{x-2}{2}\right)^{2}} \\ \text{(iii)} \quad f(x) & =\begin{cases} \frac{1}{\sqrt{2 \pi x}} e^{-x / 2}, & \text{for }x > 0 \\ 0, & \text{elsewhere.} \end{cases} \\ \\ \text{(iv)} \quad f(x) & =\begin{cases} \frac{1}{4} x e^{-x / 2}, & \text{for }x > 0 \\ 0, & \text{elsewhere.} \end{cases} \\ \end{align}
Show that each of the functions \(p(\cdot)\) given in exercises 2.6 and 2.7 is a probability mass function [by showing that it satisfies (2.8) ], and sketch its graph.
Hint : use freely the facts developed in the appendix to this section.
2.6. \begin{align} \text{(i)} \quad p(x) & =\begin{cases} \dfrac{1}{3}, & \text{for } x = 0 \\[6pt] \dfrac{2}{3}, & \text{for } x = 1 \\[6pt] 0, & \text{elsewhere.} \end{cases} \\ \\ \text{(ii)} \quad p(x) & =\begin{cases} \displaystyle {6\choose x}\left(\frac{2}{3}\right)^{x}\left(\frac{1}{3}\right)^{6-x}, & \text{for } x= 0, 1, \dots, 6 \\[6pt] 0, & \text{elsewhere.} \end{cases} \\ \\ \text{(iii)} \quad p(x) & =\begin{cases} \dfrac{2}{3}\left(\dfrac{1}{3}\right)^{x-1}, & \text{for } x=1, 2, \dots, \\[2mm] 0, & \text{elsewhere.} \end{cases} \\ \\ \text{(iv)} \quad p(x) & =\begin{cases} e^{-2} \dfrac{2^{x}}{x !}, & \text{for } x=1, 2, \dots, \\[2mm] 0, & \text{elsewhere.} \end{cases} \end{align}
2.7. \begin{align} \text{(i)} \quad p(x) & =\begin{cases} \frac{\left(\begin{array}{l} 8 \\ x \end{array}\right)\left(\begin{array}{c} 4 \\ 6-x \end{array}\right)}{\left(\begin{array}{c} 12 \\ 6 \end{array}\right)}, & \text{for } x=0, 1, 2, 4, 5, 6 \\ 0, & \text{elsewhere.} \end{cases} \\ \\ \text{(ii)} \quad p(x) & =\begin{cases} \left(\begin{array}{c} 1+x \\ x \end{array}\right)\left(\frac{2}{3}\right)^{2}\left(\frac{1}{3}\right)^{x}, & \text{for } x=0, 1, 2, \dots \\ 0, & \text{elsewhere.} \end{cases} \\ \\ \text{(iii)} \quad p(x) & =\begin{cases} \frac{\left(\begin{array}{c}-8 \\ x\end{array}\right)\left(\begin{array}{c}-4 \\ 6-x\end{array}\right)}{\left(\begin{array}{c}-12 \\ 6\end{array}\right)}, & \text{for } x=0, 1, 2, 4, 5, 6 \\ 0, & \text{elsewhere.} \end{cases} \\ \end{align}
2.8. The amount of bread (in hundreds of pounds) that a certain bakery is able to sell in a day is found to be a numerical-valued random phenomenon, with a probability function specified by the probability density function \(f(\cdot)\) , given by
\begin{align} f(x) = \begin{cases} A x, & \text{for } 0 \leq x < 5 \\[2mm] A(10 - x), & \text{for } 5 \leq x < 10 \\[2mm] 0, & \text{otherwise} \end{cases} \end{align}
- Find the value of \(A\) which makes \(f(\cdot)\) a probability density function.
- Graph the probability density function.
- What is the probability that the number of pounds of bread that will be sold tomorrow is (a) more than 500 pounds, \((b)\) less than 500 pounds, (c) between 250 and 750 pounds?
- Denote, respectively, by \(A, B\) , and \(C\) , the events that the number of pounds of bread sold in a day is ( \(a\) ) greater than 500 pounds, \((b)\) less than 500 pounds, \((c)\) between 250 and 750 pounds. Find \(P[A \mid B], P[A \mid C]\) . Are \(A\) and \(B\) independent events? Are \(A\) and \(C\) independent events?
2.9. The length of time (in minutes) that a certain young lady speaks on the telephone is found to be a random phenomenon, with a probability function specified by the probability density function \(f(\cdot)\) , given by \begin{align} f(x) = \begin{cases} A e^{-\frac{x}{5}}, & \text{for } x > 0 \\[2mm] 0, & \text{otherwise.} \end{cases} \end{align}
(i) Find the value of \(A\) that makes \(f(\cdot)\) a probability density function.
(ii) Graph the probability density function.
(iii) What is the probability that the number of minutes that the young lady will talk on the telephone is \((a)\) more than 10 minutes, \((b)\) less than 5 minutes, \((c)\) between 5 and 10 minutes?
(iv) For any real number \(b\) , let \(A(b)\) denote the event that the young lady talks longer than \(b\) minutes. Find \(P[A(b)]\) . Show that, for \(a>0\) and \(b>0, P[A(a+b) \mid A(a)]=P[A(b)]\) . In words, the conditional probability that a telephone conversation will last more than \(a+b\) minutes, given that it has lasted at least \(a\) minutes, is equal to the unconditional probability that it will last more than \(b\) minutes.
Answer
(i) \(A=\frac{1}{5}\) ; (iii) (a) 0.1353, (b) 0.6321, (c) 0.2326; (iv) \(P[A(b)]=e^{-b / 5}\) .
2.10. The number of newspapers that a certain newsboy is able to sell in a day is found to be a numerical-valued random phenomenon, with a probability function specified by the probability mass function \(p(\cdot)\) , given by
\begin{align} p(x) = \begin{cases} A x, & \text{for } x = 1, 2, \ldots, 50 \\[2mm] A(100 - x), & \text{for } x = 51, 52, \ldots, 100 \\[2mm] 0, & \text{otherwise.} \end{cases} \end{align}
(i) Find the value of \(A\) that makes \(p(\cdot)\) a probability mass function.
(ii) Sketch the probability mass function.
(iii) What is the probability that the number of newspapers that will be sold tomorrow is (a) more than 50, (b) less than 50, (c) equal to 50, (d) between 25 and 75, inclusive, (e) an odd number?
(iv) Denote, respectively, by \(A, B, C\) , and \(D\) , the events that the number of newspapers sold in a day is (a) greater than \(50,(b)\) less than \(50,(c)\) equal to 50, (d) between 25 and 75, inclusive. Find \(P[A \mid B], P[A \mid C], P[A \mid D]\) , \(P[C \mid D]\) . Are \(A\) and \(B\) independent events? Are \(A\) and \(D\) independent events? Are \(C\) and \(D\) independent events?
2.11. The number of times that a certain piece of equipment (say, a light switch) operates before having to be discarded is found to be a random phenomenon, with a probability function specified by the probability mass function \(p(\cdot)\) , given by
\begin{align} p(x) = \begin{cases} A\left(\frac{1}{3}\right)^{x}, & \text{for } x = 0, 1, 2, \ldots \\[2mm] 0, & \text{otherwise.} \end{cases} \end{align}
(i) Find the value of \(A\) which makes \(p(\cdot)\) a probability mass function.
(ii) Sketch the probability mass function.
(iii) What is the probability that the number of times the equipment will operate before having to be discarded is (a) greater than \(5,(b)\) an even number (regard 0 as even), (c) an odd number?
(iv) For any real number \(b\) , let \(A(b)\) denote the event that the number of times the equipment operates is strictly greater than or equal to \(b\) . Find \(P[A(b)]\) . Show that, for any integers \(a>0\) and \(b>0, P[A(a+b) \mid A(a)]=\) \(P[A(b)]\) . Express in words the meaning of this formula.
Answer
(i) \(A=\frac{2}{3}\) ; (iii) (a) \(\left(\frac{1}{3}\right)^{6}\) , (b) \(\frac{3}{4}\) , (c) \(\frac{1}{4}\) ; (iv) \(P[A(b)]=\left(\frac{1}{3}\right)^{b}\) .
Appendix: The Evaluation of Integrals and Sums
If (2.1) and (2.7) are to be useful expressions for evaluating the probability of an event, then techniques must be available for evaluating sums and integrals. The purpose of this appendix is to state some of the notions and formulas with which the student should become familiar and to collect some important formulas that the reader should learn to use, even if he lacks the mathematical background to justify them.
To begin with, let us note the following principle. If a function is defined by different analytic expressions over various regions, then to evaluate an integral whose integrand is this function one must express the integral as a sum of integrals corresponding to the different regions of definition of the function . For example, consider the probability density function \(f(\cdot)\) defined by \begin{align} f(x) = \begin{cases} x, & \text{for } 0 < x < 1 \\[2mm] 2 - x, & \text{for } 1 < x < 2 \\[2mm] 0, & \text{elsewhere.} \end{cases} \end{align} To prove that \(f(\cdot)\) is a probability density function, we need to verify that (2.2) and (2.3) are satisfied. Clearly, (2.3) holds. Next, \begin{align} \int_{-\infty}^{\infty} f(x) d x & =\int_{0}^{2} f(x) d x+\int_{-\infty}^{0} f(x) d x+\int_{2}^{\infty} f(x) d x \\ & =\int_{0}^{1} f(x) d x+\int_{1}^{2} f(x) d x+0 \\ & =\left.\frac{x^{2}}{2}\right|_{0} ^{1}+\left.\left(2 x-\frac{x^{2}}{2}\right)\right|_{1} ^{2}=\frac{1}{2}+\left(2-\frac{3}{2}\right)=1, \end{align} and (2.2) has been shown to hold. It might be noted that the function \(f(\cdot)\) in (2.10) can be written somewhat more concisely in terms of the absolute value notation: \begin{align} f(x) = \begin{cases} 1 - |1 - x|, & \text{for } 0 \leq x \leq 2 \\[2mm] 0, & \text{otherwise} \end{cases} \end{align} Next, in order to check his command of the basic techniques of integration, the reader should verify that the following formulas hold: \[\int \frac{e^{x}}{\left(1+e^{x}\right)^{2}} d x=\frac{-1}{1+e^{x}}, \quad \int \frac{e^{x}}{1+e^{2 x}} d x=\tan ^{-1} e^{x}=\arctan e^{x},\] \[\int e^{-x-e^{-x}} d x=\int e^{-e^{-x}} e^{-x} d x=e^{-e^{-x}}. \tag{2.12}\]
An important integration formula, obtained by integration by parts, is the following, for any real number \(t\) for which the integrals make sense: \[\int x^{t-1} e^{-x} \cdot d x=-x^{t-1} e^{-x}+(t-1) \int x^{t-2} e^{-x} d x \tag{2.13}\] Thus, for \(t=2\) we obtain \[\int x e^{-x} d x=-x e^{-x}+\int e^{-x} d x=-e^{-x}(x+1). \tag{2.14}\]
We next consider the Gamma function \(\Gamma(\cdot)\) , which plays an important role in probability theory. It is defined for every \(t>0\) by \[\Gamma(t)=\int_{0}^{\infty} x^{t-1} e^{-x} dx. \tag{2.15}\]
The Gamma function is a generalization of the factorial function in the following sense. From (2.13) it follows that \[\Gamma(t)=(t-1) \Gamma(t-1) . \tag{2.16}\] Therefore, for any integer \(r, 0 \leq r<t\) , \[\Gamma(t+1)=t \Gamma(t)=t(t-1) \cdots(t-r) \Gamma(t-r) . \tag{2.17}\] Since, clearly, \(\Gamma(1)=1\) , it follows that for any integer \(n \geq 0\) \[\Gamma(n+1)=n ! \tag{2.18}\]
Next, it may be shown that for any integer \(n>0\) \[\Gamma\left(n+\frac{1}{2}\right)=\frac{1 \cdot 3 \cdot 5 \cdots(2 n-1)}{2^{n}} \sqrt{\pi}, \tag{2.19}\] which may be written for any even integer \(n\) \[\Gamma\left(\frac{n+1}{2}\right)=\frac{1 \cdot 3 \cdot 5 \cdots(n-1)}{2^{n / 2}} \sqrt{\pi}, \tag{2.20}\] since \[\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi} . \tag{2.21}\]
We prove (2.21) by showing that \(\Gamma\left(\frac{1}{2}\right)\) is equal to another integral of whose value we have need. In (2.15) , make the change of variable \(x=\frac{1}{2} y^{2}\) , and let \(t=(n+1) / 2\) . Then, for any integer, \(n=0,1, \ldots\) , we have the formula \[\Gamma\left(\frac{n+1}{2}\right)=\frac{1}{2^{(n-1) / 2}} \int_{0}^{\infty} y^{n} e^{-1 / 2 y^{2}} dy. \tag{2.22}\]
In view of (2.22) , to establish (2.21) we need only show that \[\Gamma\left(\frac{1}{2}\right)=\sqrt{2} \int_{0}^{\infty} e^{-1 / 2 y^{2}} d y=\frac{1}{\sqrt{2}} \int_{-\infty}^{\infty} e^{-1 / 2 y^{2}} d y=\sqrt{\pi}. \tag{2.23}\]
We prove (2.23) by proving the following basic formula; for any \(u>0\) \[\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} e^{-\frac{1}{2} u y^{2}} d y=\frac{1}{\sqrt{u}}. \tag{2.24}\]
Equation (2.24) may be derived as follows. Let \(I\) be the value of the integral in (2.24) . Then \(I^{2}\) is a product of two single integrals. By the theorem for the evaluation of double integrals, it then follows that \[I^{2}=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \exp \left[-\frac{1}{2} u\left(x^{2}+y^{2}\right)\right] dx dy. \tag{2.25}\]
We now evaluate the double integral in (2.25) by means of a change of variables to polar coordinates. Then \[I^{2}=\frac{1}{2 \pi} \int_{0}^{2 \pi} \int_{0}^{\infty} e^{-\frac{1}{2} u r^{2}} r d r d \theta=\int_{0}^{\infty} e^{-\frac{1}{2} u r^{2}} r d r=\frac{1}{u},\] so that \(I=1 / \sqrt{u}\) , which proves (2.24) .
For large values of \(t\) there is an important asymptotic formula for the Gamma function, which is known as Stirling’s formula . Taking \(t=n+1\) , in which \(n\) is a positive integer, this formula can be written \begin{align} \log n ! & =\left(n+\frac{1}{2}\right) \log n-n+\frac{1}{2} \log 2 \pi+\frac{r(n)}{12 n}, \\[2mm] n! & =\left(\frac{n}{e}\right)^{n} \sqrt{2 \pi n} e^{r(n) / 12 n}, \tag{2.26} \end{align} in which \(r(n)\) satisfies \(1-1 /(12 n+1)<r(n)<1\) . The proof of Stirling’s formula may be found in many books. A particularly clear derivation is given by H. Robbins, “A Remark on Stirling’s Formula”, American Mathematical Monthly , Vol. 62 (1955), pp. 26–29.
We next turn to the evaluation of sums and infinite sums . The major tool in the evaluation of infinite sums is Taylor’s theorem, which states that under certain conditions a function \(g(x)\) may be expanded in a power series: \[g(x)=\sum_{k=0}^{\infty} \frac{x^{k}}{k !} g^{(k)}(0), \tag{2.27}\] in which \(g^{(k)}(0)\) denotes the value at \(x=0\) of the \(k\) th derivative \(g^{(k)}(x)\) of \(g(x)\) . Letting \(g(x)=e^{x}\) , we obtain \[e^{x}=\sum_{k=0}^{\infty} \frac{x^{k}}{k !}=1+x+\frac{x^{2}}{2 !}+\cdots+\frac{x^{n}}{n !}+\cdots,-\infty<x<\infty. \tag{2.28}\]
Take next \(g(x)=(1-x)^{n}\) , in which \(n=1,2, \ldots\) Clearly \begin{align} g^{(k)}(x) = \begin{cases} (-1)^{k}(n)_{k}(1 - x)^{n - k}, & \text{for } k = 0, 1, \ldots, n \\[2mm] 0, & \text{for } k > n. \end{cases} \end{align}
Consequently, for \(n=1,2, \ldots\) \[(1-x)^{n}=\sum_{k=0}^{n}(-1)^{k}\left(\begin{array}{l} n \tag{2.30} \\ k \end{array}\right) x^{k}, \quad-\infty<x<\infty\] which is a special case of the binomial theorem. One may deduce the binomial theorem from (2.30) by setting \(x=(-b) / a\) .
We obtain an important generalization of the binomial theorem by taking \(g(x)=(1-x)^{t}\) , in which \(t\) is any real number. For any real number \(t\) and any integer \(k=1,2, \ldots\) define the binomial coefficient \begin{align} \binom{t}{k} = \begin{cases} \frac{t(t-1) \cdots (t-k+1)}{k!}, & \text{for } k = 1, 2, \ldots \tag{2.31} \\[2mm] 1, & \text{for } k = 0 \end{cases} \end{align}
Note that for any positive number \(n\) \begin{align} \left(\begin{array}{c}-n \\ k\end{array}\right) & =(-1)^{k} \frac{n(n+1) \cdots(n+k-1)}{k !} \\ & =(-1)^{k}\left(\begin{array}{c}n+k-1 \\ k\end{array}\right). \tag{2.32} \end{align}
By Taylor’s theorem, we obtain the important formula for all real numbers \(t\) and \(-1<x<1\) , \[(1-x)^{t}=\sum_{k=0}^{\infty}\left(\begin{array}{l} t \tag{2.33} \\ k \end{array}\right)(-x)^{k}.\]
For the case of \(n\) positive we may write, in view of (2.32) , \[(1-x)^{-n}=\sum_{k=0}^{\infty}\left(\begin{array}{c} n+k-1 \tag{2.34} \\ k \end{array}\right) x^{k}, \quad|x|<1\]
Equation (2.34) , with \(n=1\) , is the familiar formula for the sum of a geometric series: \[\sum_{k=0}^{\infty} x^{k}=1+x+x^{2}+\cdots+x^{n}+\cdots=\frac{1}{1-x}, \quad|x|<1 . \tag{2.35}\]
Equation (2.34) with \(n=2\) and 3 yields the formulas \begin{align} & \sum_{k=0}^{\infty}(k+1) x^{k}=1+2 x+3 x^{2}+\cdots=\frac{1}{(1-x)^{2}}, \quad|x|<1, \tag{2.36} \\ & \sum_{k=0}^{\infty}(k+2)(k+1) x^{k}=\frac{2}{(1-x)^{3}}, \quad|x|<1 . \end{align}
From (2.33) we may obtain another important formula. By a comparison of the coefficients of \(x^{n}\) on both sides of the equation \[(1+x)^{s}(1+x)^{t}=(1+x)^{s+t},\] we obtain for any real numbers \(s\) and \(t\) and any positive integer \(n\) \[\left(\begin{array}{l} s \tag{2.37} \\ 0 \end{array}\right)\left(\begin{array}{l} t \\ n \end{array}\right)+\left(\begin{array}{l} s \\ 1 \end{array}\right)\left(\begin{array}{c} t \\ n-1 \end{array}\right)+\cdots+\left(\begin{array}{l} s \\ n \end{array}\right)\left(\begin{array}{l} t \\ 0 \end{array}\right)=\left(\begin{array}{c} s+t \\ n \end{array}\right).\]
If \(s\) and \(t\) are positive integers (2.37) could be verified by mathematical induction. A useful special case of (2.37) is when \(s=t=n\) ; we then obtain (5.13) of Chapter 2 .
Theoretical Exercises
2.1 . Show that for any positive real numbers \(\alpha, \beta\) , and \(t\)
\begin{align} \int_{0}^{\infty} x^{\beta-1} e^{-\alpha x} d x & =\frac{\Gamma(\beta)}{\alpha^{\beta}} \\ \frac{\alpha^{\beta}}{\Gamma(\beta)} \int_{0}^{\infty} e^{-t x} x^{\beta-1} e^{-\alpha x} d x & =\left(1+\frac{t}{\alpha}\right)^{-\beta} . \tag{2.38} \end{align}
2.2 . Show for any \(\sigma>0\) and \(n=1,2, \ldots\) \[2 \int_{0}^{\infty} y^{n} e^{-\frac{1}{2}(y / \sigma)^{2}} d y=\left(2 \sigma^{2}\right)^{(n+1) / 2} \Gamma\left(\frac{n+1}{2}\right). \tag{2.39}\]
2.3 . The integral \[B(m, n)=\int_{0}^{1} x^{m-1}(1-x)^{n-1} dx, \tag{2.40}\] which converges if \(m\) and \(n\) are positive, defines a function of \(m\) and \(n\) , called the beta function . Show that the beta function is symmetrical in its arguments, \(B(m, n)=B(n, m)\) , and may be expressed [letting \(x=\sin ^{2} \theta\) and \(x=1 /(1+y)\) , respectively] by \begin{align} B(m, n) & =2 \int_{0}^{\pi / 2} \sin ^{2 m-1} \theta \cos ^{2 n-1} \theta d \theta \tag{2.41} \\ & =\int_{0}^{\infty} \frac{y^{n-1}}{(1+y)^{m+n}} dy. \end{align}
Show finally that the beta and gamma functions are connected by the relation \[B(m, n)=\frac{\Gamma(m) \Gamma(n)}{\Gamma(m+n)}. \tag{2.42}\] Hint: By changing to polar coordinates, we have \begin{align} \Gamma(m) \Gamma(n) & =4 \int_{0}^{\infty} \int_{0}^{\infty} x^{2 m-1} e^{-x^{2}} y^{2 n-1} e^{-y^{2}} d x d y \\ & =4 \int_{0}^{\pi / 2} d \theta \cos ^{2 m-1} \theta \sin ^{2 n-1} \theta \int_{0}^{\infty} d r e^{-r^{2} r^{2 m+2 n-1}} . \end{align}
2.5 . Prove that the integral defining the gamma function converges for any real number \(t>0\) .
2.6 . Prove that the integral defining the beta function converges for any real numbers \(m\) and \(n\) , such that \(m>0\) and \(n>0\) .
2.7 . Taylor’s theorem with remainder . Show that if the function \(g(\cdot)\) has a continuous \(n\) th derivative in some interval containing the origin then for \(x\) in this interval
\begin{align} g(x)=g(0)+x g^{\prime}(0)+\frac{x^{2}}{2 !} g^{\prime \prime}(0) & +\cdots+\frac{x^{n-1}}{(n-1) !} g^{(n-1)}(0). \tag{2.43} \\ & +\frac{x^{n}}{(n-1) !} \int_{0}^{1} d t(1-t)^{n-1} g^{(n)}(x t) \end{align} Hint : Show, for \(k=2,3, \ldots, n\) , that \begin{align} -\frac{x^{k}}{(k-1) !} \int_{0}^{1} g^{(k)}(x t)(1-t)^{k-1} d t+\frac{x^{k-1}}{(k-2) !} \int_{0}^{1} g^{(k-1)}&(x t)(1-t)^{k-2} d t \\ &=\frac{x^{k-1}}{(k-1) !} g^{(k-1)}(0). \end{align}
2.8 . Lagrange’s form of the remainder in Taylor’s theorem . Show that if \(g(\cdot)\) has a continuous \(n\) th derivative in the closed interval from 0 to \(x\) , where \(x\) may be positive or negative, then \[\int_{0}^{1} g^{(n)}(x t)(1-t)^{n-1} d t=\frac{1}{n} g^{(n)}(\theta x) \tag{2.44}\] for some number \(\theta\) in the interval \(0<\theta<1\) .
- We usually assume that the integral in (2.1) is defined in the sense of Riemann; to ensure that this is the case, we require that the function \(f(\cdot)\) be defined and continuous at all but a finite number of points. The integral in (2.1) is then defined only for events \(E\) , which are either intervals or unions of a finite number of non-overlapping intervals. In advanced probability theory the integral in (2.1) is defined by means of a theory of integration developed in the early 1900’s by Henri Lebesgue. The function \(f(\cdot)\) must then be a Borel function, by which is meant that for any real number \(c\) the set \(\{x: f(x)<c\}\) is a Borel set. A function that is continuous at all but a finite number of points may be shown to be a Borel function. It may be shown that if a Borel function \(f(\cdot)\) satisfies (2.1) and (2.3) then, for any Borel set \(B\) , the integral of \(f(\cdot)\) over \(B\) exists as an integral defined in the sense of Lebesgue. If \(B\) is an interval, or a union of a finite number of non-overlapping intervals, and if \(f(\cdot)\) is continuous on \(B\) , then the integral of \(f(\cdot)\) over \(B\) , defined in the sense of Lebesgue, has the same value as the integral of \(f(\cdot)\) over \(B\) , defined in the sense of Riemann. Henceforth, in this book the word function (unless otherwise qualified) will mean a Borel function and the word set (of real numbers) will mean a Borel set. ↩︎
- For the purposes of this book we also require that a probability density function \(f(\cdot)\) be defined and continuous at all but a finite number of points. ↩︎
- The reader should note the convention used in the exercises of this book. When a function \(f(\cdot)\) is defined by a single analytic expression for all \(x\) in \(-\infty<x<\infty\) , the fact that \(x\) varies between \(-\infty\) and \(\infty\) is not explicitly indicated. ↩︎