From a knowledge of the mean and variance of a probability law one cannot in general determine the probability law. In the circumstance that the functional form of the probability law is known up to several unspecified parameters (for example, a probability law may be assumed to be a normal distribution with parameters \(m\) and \(\sigma\) ), it is often possible to relate the parameters and the mean and variance. One may then use a knowledge of the mean and variance to determine the probability law. In the case in which the functional form of the probability law is unknown one can obtain crude estimates of the probability law, which suffice for many purposes, from a knowledge of the mean and variance.

For any probability law with finite mean \(m\) and finite variance \(\sigma^{2}\) , define the quantity \(Q(h)\) , for any \(h>0\) , as the probability assigned to the interval \(\{x: m-h \sigmaby the probability law. In terms of a distribution function \(F(\cdot)\) or a probability density function \(f(\cdot)\) ,

\[Q(h)=F(m+h \sigma)-F(m-h \sigma)=\int_{m-h \sigma}^{m+h \sigma} f(x) dx. \tag{4.1}\] 

Let us compute \(Q(h)\) in certain cases. For the normal probability law with mean \(m\) and standard deviation \(\sigma\) 

\[Q(h)=\frac{1}{\sqrt{2 \pi} \sigma} \int_{m-h \sigma}^{m+h \sigma} e^{-\frac{1}{2}\left(\frac{y-m}{\sigma}\right)^{2}} d y=\Phi(h)-\Phi(-h). \tag{4.2}\] 

For the exponential law with mean \(1 / \lambda\) \begin{align} Q(h) =\begin{cases} e^{-1}\left(e^{h}-e^{-h}\right), & \text { for } h \leq 1 \tag{4.3} \\[2mm] 1-e^{-(1+h)}, & \text { for } h \geq 1. \end{cases} \end{align} 

For the uniform distribution over the interval \(a\) to \(b\) , for \(h<\sqrt{3}\) , \[Q(h)=\frac{1}{b-a} \int_{\frac{b+a}{2}-h \frac{b-a}{\sqrt{12}}}^{\frac{b+a}{2}+h \frac{b-a}{\sqrt{12}}} d x=\frac{h}{\sqrt{3}}. \tag{4.4}\] 

For the other frequently encountered probability laws one cannot so readily evaluate \(Q(h)\) . Nevertheless, the function \(Q(h)\) is still of interest, since it is possible to obtain a lower bound for it, which does not depend on the probability law under consideration. This lower bound, known as Chebyshev’s inequality, was named after the great Russian probabilist P. L. Chebyshev (1821–1894).

Chebyshev’s inequality . For any distribution function \(F(\cdot)\) and any \(h \geq 0\) 

\[Q(h)=F(m+h \sigma)-F(m-h \sigma) \geq 1-\frac{1}{h^{2}}. \tag{4.5}\] 

Note that (4.5) is trivially true for \(h<1\) , since the right-hand side is then negative.

We prove (4.5) for the case of a continuous probability law with probability density function \(f(\cdot)\) . It may be proved in a similar manner (using Stieltjes integrals, introduced in section 6) for a general distribution function. The inequality (4.5) may be written in the continuous case

\[\int_{m-h \sigma}^{m+h \sigma} f(x) d x \geq 1-\frac{1}{h^{2}}. \tag{4.6}\] 

To prove (4.6), we first obtain the inequality

\[\sigma^{2} \geq \int_{-\infty}^{m-h \sigma}(x-m)^{2} f(x) d x+\int_{m+h \sigma}^{\infty}(x-m)^{2} f(x) d x \tag{4.7}\] 

that follows, since the variance \(\sigma^{2}\) is equal to the sum of the two integrals on the right-hand side of (4.7), plus the nonnegative quantity \(\int_{m-h \sigma}^{m+h \sigma}(x-m)^{2} f(x) d x\) . Now for \(x \leq m-h \sigma\) , it holds that \((x-m)^{2} \geq\) \(h^{2} \sigma^{2}\) . Similarly, \(x \geq m+h \sigma\) implies \((x-m)^{2} \geq h^{2} \sigma^{2}\) . By replacing \((x-m)^{2}\) by these lower bounds in (4.7), we obtain

\[\sigma^{2} \geq \sigma^{2} h^{2}\left[\int_{-\infty}^{m-h \sigma} f(x) d x+\int_{n+h \sigma}^{\infty} f(x) d x\right]. \tag{4.8}\] 

The sum of the two integrals in (4.8) is equal to \(1-Q(h)\) . Therefore (4.8) implies that \(1-Q(h) \leq\left(1 / h^{2}\right)\) , and (4.5) is proved.

In Fig.4A the function \(Q(h)\) , given by (4.2) , (4.3) , and (4.4) , and the lower bound for \(Q(h)\) , given by Chebyshev’s inequality, are plotted.

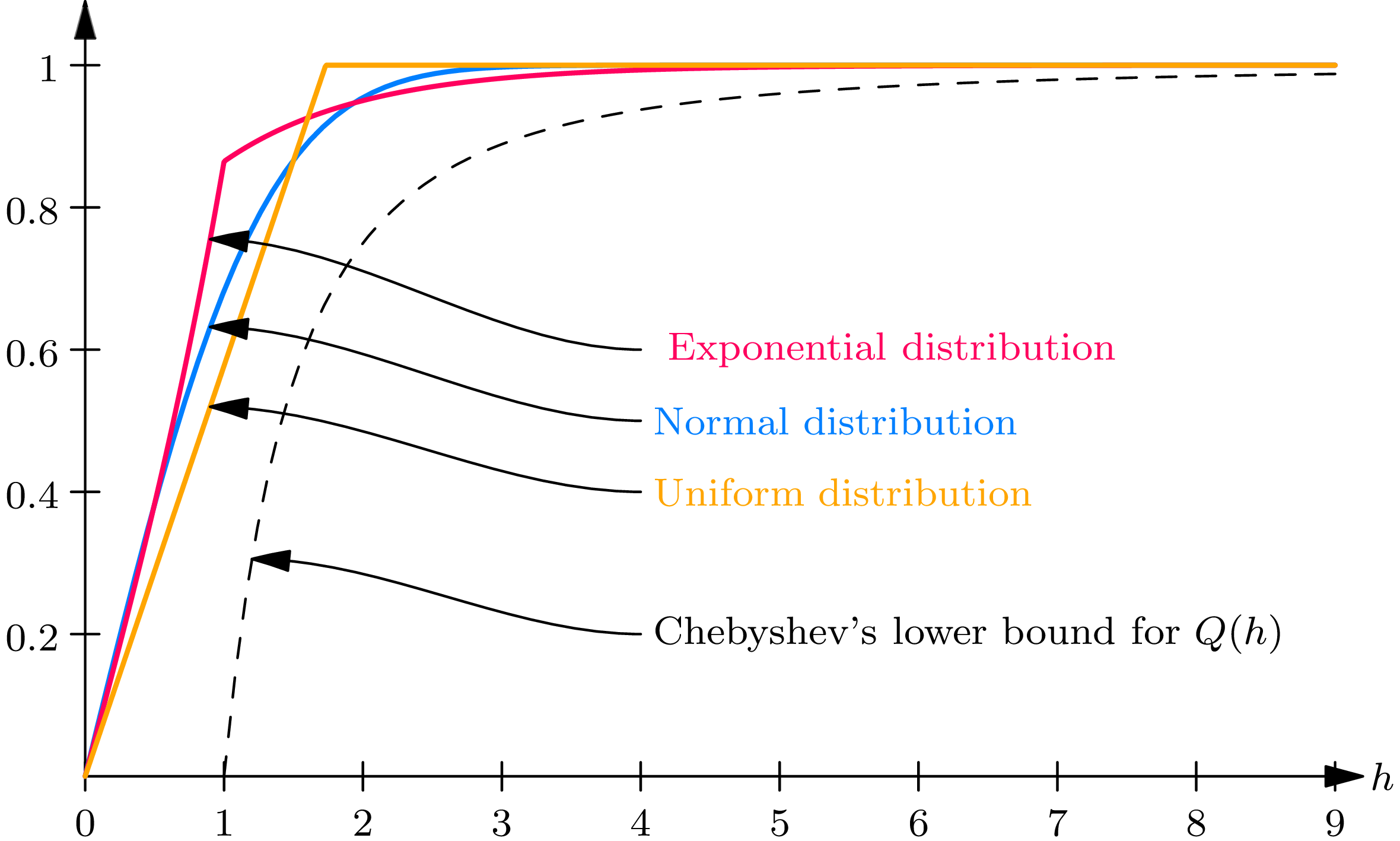
In terms of the observed value \(X\) of a numerical valued random phenomenon, Chebyshev’s inequality may be reformulated as follows. The quantity \(Q(h)\) is then essentially equal to \(P[|X-m| \leq h \sigma]\) ; in words, \(Q(h)\) is equal to the probability that an observed value of a numerical valued random phenomenon, with distribution function \(F(\cdot)\) , will lie in an interval centered at the mean and of length \(2 h\) standard deviations. Chebyshev’s inequality may be reformulated: for any \(h>0\) \[P[|X-m| \leq h \sigma] \geq 1-\frac{1}{h^{2}}, \quad P[|X-m|>h \sigma] \leq \frac{1}{h^{2}.} \tag{4.9}\] 

Chebyshev’s inequality (with \(h=4\) ) states that the probability is at least 0.9375 that an observed value \(X\) will lie within four standard deviations of the mean, whereas the probability is at least 0.99 that an observed value \(X\) will lie within ten standard deviations of the mean. Thus, in terms of the standard deviation \(\sigma\) (and consequently in terms of the variance \(\sigma^{2}\) ), we can state intervals in which, with very high probability, an observed value of a numerical valued random phenomenon may be expected to lie. It may be remarked that it is this fact that renders the variance a measure of the spread , or dispersion , of the probability mass that a probability law distributes over the real line.

Generalizations of Chebyshev’s inequality . As a practical tool for using the lower-order moments of a probability law for obtaining inequalities on its distribution function, Chebyshev’s inequality can be improved upon if various additional facts about the distribution function are known. Expository surveys of various generalizations of Chebyshev’s inequality are given by H. J. Godwin, “On generalizations of Tchebychef’s inequality”, Journal of the American Statistical Association, Vol. 50 (1955), pp. 923–945, and by C. L. Mallows, “Generalizations of Tchebycheff’s inequalities”, Journal of the Royal Statistical Society , Series B, Vol. 18 (1956), pp. 139176 (with discussion).

Exercises