Given the random variable \(X\) , we define the expectation of the random variable, denoted by \(E[X]\) , as the mean of the probability law of \(X\) ; in symbols, \begin{align} E[X] = \begin{cases} \displaystyle\int_{-\infty}^{\infty} x \, dF_{X}(x) \tag{1.1} \\[3mm] \displaystyle\int_{-\infty}^{\infty} x f_{X}(x) \, dx \\[3mm] \displaystyle\sum_{\substack{ \text{over all } x \text{ such that } \\ p_{X}(x) > 0}} x p_{X}(x), \end{cases} \end{align} depending on whether \(X\) is specified by its distribution function \(F_{X}(\cdot)\) , its probability density function \(f_{X}(\cdot)\) , or its probability mass function \(p_{X}(\cdot)\) .
Given a random variable \(Y\) , which arises as a Borel function of a random variable \(X\) so that \[Y=g(X) \tag{1.2}\] for some Borel function \(g(\cdot)\) , the expectation \(E[g(X)]\) , in view of (1.1), is given by \[E[g(X)]=\int_{-\infty}^{\infty} y\, d F_{g(X)}(y). \tag{1.3}\] On the other hand, given the Borel function \(g(\cdot)\) and the random variable \(X\) , we can form the expectation of \(g(x)\) with respect to the probability law of \(X\) , denoted by \(E_{X}[g(x)]\) and defined by \begin{align} E[X] = \begin{cases} \displaystyle\int_{-\infty}^{\infty} g(x) \, dF_{X}(x) \tag{1.1} \\[3mm] \displaystyle\int_{-\infty}^{\infty} g(x) f_{X}(x) \, dx \\[3mm] \displaystyle\sum_{\substack{ \text{over all}\; x\;\text{ such that } \\ p_{X}(x) > 0}} g(x) p_{X}(x), \end{cases} \end{align} depending on whether \(X\) is specified by its distribution function \(F_{X}(\cdot)\) , its probability density function \(f_{X}(\cdot)\) , or its probability mass function \(p_{X}(\cdot)\) .
It is a striking fact, of great importance in probability theory, that for any random variable \(X\) and Borel function \(g(\cdot)\) \[E[g(X)]=E_{X}[g(x)] \tag{1.5}\]
if either of these expectations exists . In words, (1.5) says that the expectation of the random variable \(g(X)\) is equal to the expectation of the function \(g(\cdot)\) with respect to the random variable \(X\) .
The validity of (1.5) is a direct consequence of the fact that the integrals used to define expectations are required to be absolutely convergent. 1 Some idea of the proof of (1.5), in the case that \(g(\cdot)\) is continuous, can be gained. Partition the \(y\) -axis in Fig. 1A into subintervals by points \(y_{0}
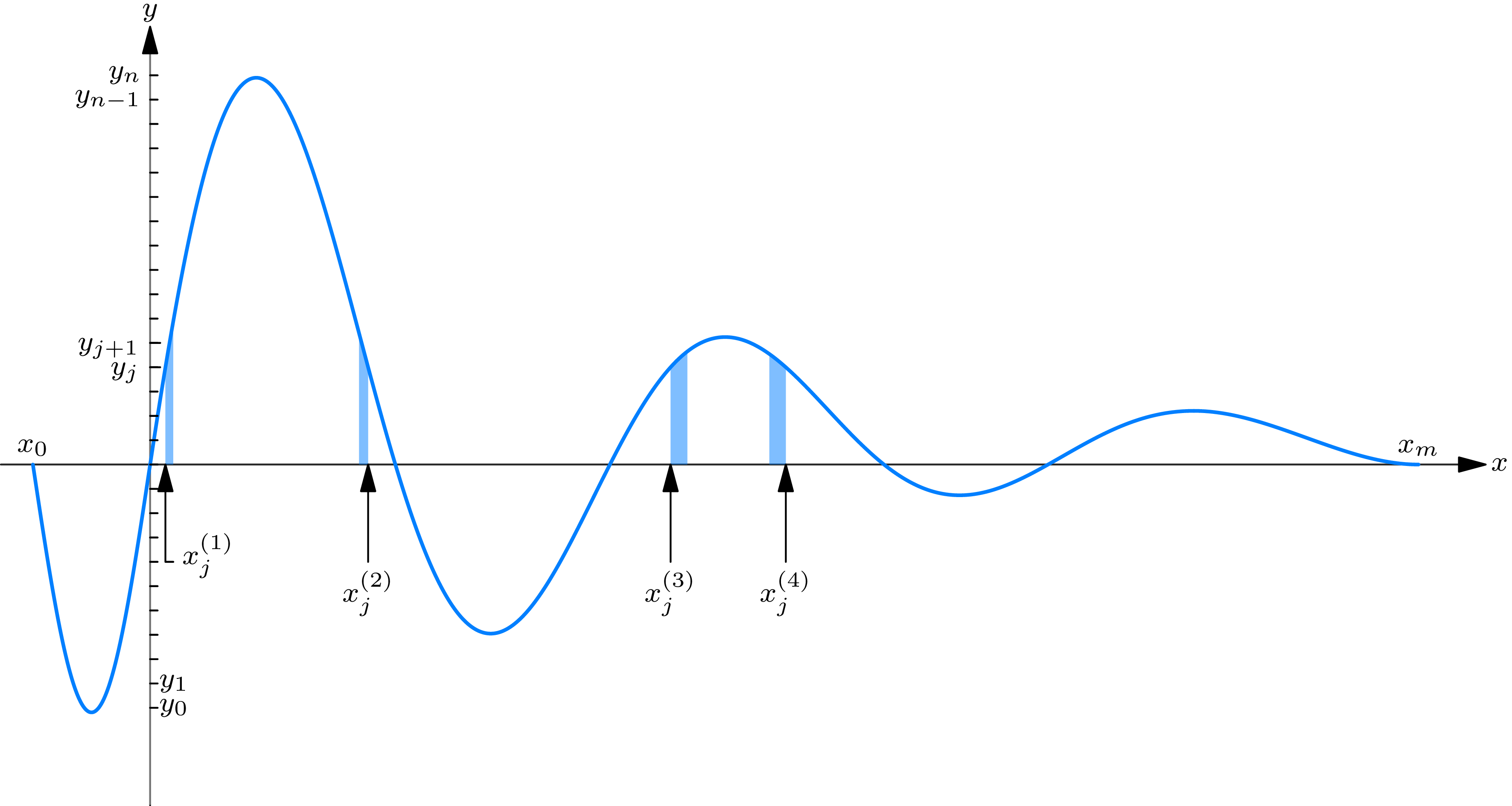
Given a random variable \(X\) and a function \(g(\cdot)\) , we thus find two distinct notions, represented by \(E[g(X)]\) and \(E_{X}[g(x)]\) , which nevertheless, are always numerically equal. It has become customary always to use the notation \(E[g(X)]\) , since this notation is the most convenient for technical manipulation. However, the reader should be aware that although we write \(E[g(X)]\) the concept in which we are really very often interested is \(E_{X}[g(x)]\) , the expectation of the function \(g(x)\) with respect to the random variable \(X\) . Thus, for example, the \(n\) th moment of a random variable \(X\) (for any integer \(n\) ) is often defined as \(E\left[X^{n}\right]\) , the expectation of the \(n\) th power of \(X\) . From the point of view of the intuitive meaning of the \(n\) th moment, however, it should be defined as the expectation \(E_{X}\left[x^{n}\right]\) of the function \(g(x)=x^{n}\) with respect to the probability law of the random variable \(X\) . We shall define the moments of a random variable in terms of the notation of the expectation of a random variable. However, it should be borne in mind that we could define as well the moments of a random variable as the corresponding moments of the probability law of the random variable.
Given a random variable \(X\) , we denote its mean by \(E[X]\) , its mean square by \(E\left[X^{2}\right]\) , its square mean by \(E^{2}[X]\) , its \(n\) th moment about the point \(c\) by \(E\left[(X-c)^{n}\right]\) , and its \(n\) th central moment (that is, \(n\) th moment about its mean) by \(E\left[(X-E[X])^{n}\right]\) . In particular, the variance of a random variable, denoted by Var \([X]\) , is defined as its second central moment, so that \[\operatorname{Var}[X]=E\left[(X-E[X])^{2}\right]=E\left[X^{2}\right]-E^{2}[X]. \tag{1.8}\] The standard deviation of a random variable, denoted by \(\sigma[X]\) , is defined as the positive square root of its variance, so that \[\sigma[X]=\sqrt{\operatorname{Var}[X]}, \quad \sigma^{2}[X]=\operatorname{Var}[X]. \tag{1.9}\] The moment generating function of a random variable, denoted by \(\psi_{X}(\cdot)\) , is defined for every real number \(t\) by \[\psi_{X}(t)=E\left[e^{t X}\right]. \tag{1.10}\]
It is shown in section 5 that if \(X_{1}, X_{2}, \ldots, X_{n}\) constitute a random sample of the random variable \(X\) then the arithmetic mean \(\left(X_{1}+X_{2}+\cdots+X_{n}\right) / n\) is, for large \(n\) , approximately equal to the mean \(E[X]\) . This fact has led early writers on probability theory to call \(E[X]\) the expected value of the random variable \(X\) ; this terminology, however, is somewhat misleading, for if \(E[X]\) is the expected value of any random variable it is the expected value of the arithmetic mean of a random sample of the random variable.
Example 1A . he mean duration of the game of “odd man out.” The game of “odd man out” was described in example 3D of Chapter 3. On each independent play of the game, \(N\) players independently toss fair coins. The game concludes when there is an odd man; that is, the game concludes the first time that exactly one of the coins falls heads or exactly one of the coins falls tails. Let \(X\) be the number of plays required to conclude the game; more briefly, \(X\) is called the duration of the game. Find the mean and standard deviation of \(X\) .
Solution
It has been shown that the random variable \(X\) obeys a geometric probability law with parameter \(p=\frac{N}{2^{N-1}}\) . The mean of \(X\) is then equal to the mean of the geometric probability law, so that \(E[X]=1 / p\) . Similarly, \(\sigma^{2}[X]=q / p^{2}\) . Thus, if \(N=5, E[X]=\frac{2^{4}}{5}=3.2\) , \(\sigma^{2}[X]=(11 / 16) /(5 / 16)^{2}=(11)(16) / 25\) , and \(\sigma[X]=4 \sqrt{11} / 5=2.65\) . The mean duration \(E[X]\) has the following interpretation; if \(X_{1}, X_{2}, \ldots, X_{n}\) are the durations of \(n\) independent games of “odd man out”, then the average duration \(\left(X_{1}+X_{2}+\cdots+X_{n}\right) / n\) of the \(n\) games is approximately equal to \(E[X]\) if the number \(n\) of games is large. Note that in a game with five players the mean duration \(E[X](=3.2)\) is not equal to an integer. Consequently, one will never observe a game whose duration is equal to the mean duration; nevertheless, the arithmetic mean of a large number of observed durations can be expected to be equal to the mean duration.
To find the mean and variance of the random variable \(X\) , in the foregoing example we found the mean and variance of the probability law of \(X\) . If a random variable \(Y\) can be represented as a Borel function \(Y=g_{1}(X)\) of a random variable \(X\) , one can find the mean and variance of \(Y\) without actually finding the probability law of \(Y\) . To do this, we make use of an extension of (1.5).
Let \(X\) and \(Y\) be random variables such that \(Y=g_{1}(X)\) for some Borel function \(g_{1}(\cdot)\) . Then for any Borel function \(g(\cdot)\)
\[E[g(Y)]=E\left[g\left(g_{1}(X)\right)\right] \tag{1.11}\]
in the sense that if either of these expectations exists then so does the other, and the two are equal.
To prove (1.11) we must prove that
\[\int_{-\infty}^{\infty} g(y) d F_{g_{1}(X)}(y)=\int_{-\infty}^{\infty} g\left(g_{1}(x)\right) d F_{X}(x). \tag{1.12}\]
The proof of (1.12) is beyond the scope of this book.
To illustrate the meaning of (1.11), we write it for the case in which the random variable \(X\) is continuous and \(g_{1}(x)=x^{2}\) . Using the formula for the probability density function of \(Y=X^{2}\) , given by (8.8) of Chapter 7 , we have for any continuous function \(g(\cdot)\) \begin{align} E[g(Y)] & =\int_{0}^{\infty} g(y) f_{Y}(y) d y \tag{1.13} \\[3mm] & =\int_{0}^{\infty} g(y) \frac{1}{2 \sqrt{y}}\left[f_{X}(\sqrt{y})+f_{X}(-\sqrt{y})\right] d y, \end{align} whereas \[E\left[g\left(g_{1}(X)\right)\right]=E\left[g\left(X^{2}\right)\right]=\int_{-\infty}^{\infty} g\left(x^{2}\right) f_{X}(x) dx. \tag{1.14}\] One may verify directly that the integrals on the right-hand sides of (1.13) and (1.14) are equal, as asserted by (1.11) .
As one immediate consequence of (1.11), we have the following formula for the variance of a random variable \(g(X)\) , which arises as a function of another random variable: \[\operatorname{Var}[g(X)]=E\left[g^{2}(X)\right]-E^{2}[g(X)]. \tag{1.15}\]
Example 1B . The square of a normal random variable . Let \(X\) be a normally distributed random variable with mean 0 and variance \(\sigma^{2}\) . Let \(Y=X^{2}\) . Then the mean and variance of \(Y\) are given by \(E[Y]=E\left[X^{2}\right]=\sigma^{2}\) , \(\operatorname{Var}[Y]=E\left[X^{4}\right]-E^{2}\left[X^{2}\right]=3 \sigma^{4}-\sigma^{4}=2 \sigma^{4}\) .
If a random variable \(X\) is known to be normally distributed with mean \(m\) and variance \(\sigma^{2}\) , then for brevity one often writes \(X\) is \(N\left(m, \sigma^{2}\right)\) .
Example 1C . The logarithmic normal distribution . A random variable \(X\) is said to have a logarithmic normal distribution if its logarithm \(\log X\) is normally distributed. One may find the mean and variance of \(X\) by finding the mean and variance of \(X=e^{Y}\) , in which \(Y\) is \(N\left(m, \sigma^{2}\right)\) . Now \(E[X]=E\left[e^{Y}\right]\) is the value at \(t=1\) of the moment-generating function \(\psi_{Y}(t)\) of \(Y\) . Similarly \(E\left[X^{2}\right]=E\left[e^{2 Y}\right]=\psi_{Y}(2)\) . Since \(\psi_{Y}(t)=\exp (m t+\) \(\left.\frac{1}{2} \sigma^{2} t^{2}\right)\) , it follows that \(E[X]=\exp \left(m+\frac{1}{2} \sigma^{2}\right)\) and \(\operatorname{Var}[X]=E\left[X^{2}\right]-E^{2}[X]=\) \(\exp \left(2 m+2 \sigma^{2}\right)-\exp \left(2 m+\sigma^{2}\right)\) .
Example 1D shows how the mean (or the expectation) of a random variable is interpreted.
Example 1D . Disadvantageous or unfair bets. Roulette is played by spinning a ball on a circular wheel, which has been divided into thirty-seven arcs of equal length, bearing numbers from 0 to 36. 2 Let \(X\) denote the number of the arc on which the ball comes to rest. Assume each arc is equally likely to occur, so that the probability mass function of \(X\) is given by \(p_{X}(x)=\frac{1}{37}\) for \(x=0,1, \ldots, 36\) . Suppose that one is given even odds on a bet that the observed value of \(X\) is an odd number; that is, on a 1 dollar bet one is paid 2 dollars (including one’s stake) if \(X\) is odd, and one is paid nothing (so that one loses one’s stake) if \(X\) is not odd. How much can one expect to win at roulette by consistently betting on an odd outcome?
Solution
Define a random variable \(Y\) as equal to the amount won by betting 1 dollar on an odd outcome at a play of the game of roulette. Then \(Y=1\) if \(X\) is odd and \(Y=-1\) if \(X\) is not odd. Consequently, \(P[Y=1]=\frac{18}{37}\) and \(P[Y=-1]=\frac{19}{37}\) . The mean \(E[Y]\) of the random variable \(Y\) is then given by
\[E[Y]=1 \cdot p_{Y}(1)+(-1) \cdot p_{Y}(-1)=-\frac{1}{37}=-0.027. \tag{1.16}\]
The amount one can expect to win at roulette by betting on an odd outcome may be regarded as equal to the mean \(E[Y]\) in the following sense. Let \(Y_{1}, Y_{2}, \ldots, Y_{n}, \ldots\) be one’s winnings in a succession of plays of roulette at which one has bet on an odd outcome. It is shown in section 5 that the average winnings \(\frac{Y_{1}+Y_{2}+\cdots+Y_{n}}{n}\) in \(n\) plays tends, as the number of plays becomes infinite, to \(E[Y]\) . The fact that \(E[Y]\) is equal to a negative number implies that betting on an odd outcome at roulette is disadvantageous (or unfair) for the bettor, since after a long series of plays he can expect to have lost money at a rate of 2.7 cents per dollar bet. Many games of chance are disadvantageous for the bettor in the sense that the mean winnings is negative. However, the mean (or expected) winnings describe just one aspect of what will occur in a long series of plays. For a gambler who is interested only in a modest increase in his fortune it is more important to know the probability that as a result of a series of bets on an odd outcome in roulette the size of his 1000-dollar fortune will increase to 1200 dollars before it decreases to zero. A home owner insures his home against destruction by fire, even though he is making a disadvantageous bet (in the sense that his expected money winnings are negative) because he is more concerned with making equal to zero the probability of a large loss.
Most random variables encountered in applications of probability theory have finite means and variances. However, random variables without finite means have long been encountered by physicists in connection with problems of return to equilibrium. The following example illustrates a random variable of this type that has infinite mean.
Example 1E . On long leads in fair games . Consider two players engaged in a friendly game of matching pennies with fair coins. The game is played as follows. One player tosses a coin, while the other player guesses the outcome, winning one cent if he guesses correctly and losing one cent if he guesses incorrectly. The two friends agree to stop playing the moment neither is winning. Let \(N\) be the duration of the game; that is, \(N\) is equal to the number of times coins are tossed before the players are even. Find \(E[N]\) , the mean duration of the game.
Solution
It is clear that the game of matching pennies with fair coins is not disadvantageous to either player in the sense that if \(Y\) is the winnings of a given player on any play of the game then \(E[Y]=0\) . From this fact one may be led to the conclusion that the total winnings \(S_{n}\) of a given player in \(n\) plays will be equal to 0 in half the plays, over a very large number of plays. However, no such inference can be made. Indeed, consider the random variable \(N\) , which represents the first trial \(N\) at which \(S_{N}=0\) . We now show that \(E[N]=\infty\) ; in words, the mean duration of the game of matching pennies is infinite. Note that this does not imply that the duration \(N\) is infinite; it may be shown that there is probability one that in a finite number of plays the fortunes of the two players will equalize. To compute \(E[N]\) , we must compute its probability law. The duration \(N\) of the game cannot be equal to an odd integer, since the fortunes will equalize if and only if each player has won on exactly half the tosses. We omit the computation of the probability that \(N=n\) , for \(n\) an even integer, and quote here the result (see W. Feller, An Introduction to Probability Theory and its Applications, second edition , Wiley, New York, 1957, p. 75):
\[P[N=2 m]=\frac{1}{2 m}\left(\begin{array}{c} 2 m-2 \tag{1.17} \\ m-1 \end{array}\right) 2^{-2(m-1)}.\]
The mean duration of the game is then given by
\[E[N]=\sum_{m=1}^{\infty}(2 m) P[N=2 m]. \tag{1.18}\]
It may be shown, using Stirling’s formula, that
\[\left(\begin{array}{c} 2 n \tag{1.19} \\ n \end{array}\right) 2^{-2 n} \sim \frac{1}{(n \pi)^{1 / 2}},\]
the sign \(\sim\) indicating that the ratio of the two sides in (1.19) tends to 1 as \(n\) tends to infinity. Consequently, \((2 m) P[N=2 m] \geq K / \sqrt{m}\) for some constant \(K\) . Therefore, the infinite series in (1.18) diverges, and \(E[N]=\infty\) .
To conclude this section, let us justify the fact that the integrals defining expectations are required to be absolutely convergent by showing, by example, that if the expectation of a continuous random variable \(X\) is defined by
\[E[X]=\lim _{a \rightarrow \infty} \int_{-a}^{a} x f_{X}(x) dx \tag{1.20}\]
then it is not necessarily true that for any constant \(c\)
\[E[X+c]=E[X]+c.\]
Let \(X\) be a random variable whose probability density function is an even function, that is, \(f_{X}(-x)=f_{X}(x)\) . Then, under the definition given by (1.20), the mean \(E[X]\) exists and equals 0, since \(\displaystyle\int_{-a}^{a} x f_{X}(x) d x=0\) for every \(a\) . Now
\[E[X+c]=\lim _{a \rightarrow \infty} \int_{-a}^{a} y f_{X}(y-c) dy. \tag{1.21}\]
Assuming \(c>0\) , and letting \(u=y-c\) , we may write
\begin{align} \int_{-a}^{a} y f_{X}(y-c) d y & =\int_{-a-c}^{a-c}(u+c) f_{X}(u) d u \\ & =\int_{-a-c}^{a+c} u f_{X}(u) d u-\int_{a-c}^{a+c} u f_{X}(u) d u+c \int_{-a-c}^{a-c} f_{X}(u) d u \end{align}
The first of these integrals vanishes, and the last tends to 1 as \(a\) tends to \(\infty\) . Consequently, to prove that if \(E[X]\) is defined by (1.20) one can find a random variable \(X\) and a constant \(c\) such that \(E[X+c] \neq E[X]+c\) , it suffices to prove that one can find an even probability density function \(f(\cdot)\) and a constant \(c>0\) such that
\[\text { it is not so that } \lim _{a \rightarrow \infty} \int_{a-c}^{a+c} u f(u) d u=0. \tag{1.22}\]
An example of a continuous even probability density function satisfying (1.22) is the following. Letting \(A=3 / \pi^{2}\) , define
\begin{align} f(x) & = \begin{cases} A \displaystyle\frac{1}{|k|}(1 - |k - x|), & \text{if } k = \pm 1, \pm 2^{2}, \pm 3^{2}, \cdots \text{ and } |k - x| \leq 1 \\ 0, & \text{elsewhere.} \end{cases} \end{align}
In words, \(f(x)\) vanishes, except for points \(x\) , which lie within a distance 1 from a point that in absolute value is a perfect square \(1,2^{2}, 3^{2}, 4^{2}, \ldots\) . That \(f(\cdot)\) is a probability density function follows from the fact that
\[\int_{-\infty}^{\infty} f(x) d x=2 A \sum_{k=1}^{\infty} \frac{1}{k^{2}}=2 A \frac{\pi^{2}}{6}=1.\]
That (1.22) holds for \(c>1\) follows from the fact that for \(k=2^{2}, 3^{2}, \ldots\)
\[\int_{k-1}^{k+1} u f(u) d u \geq(k-1) \int_{k-1}^{k+1} f(u) d u=\frac{(k-1)}{k} A \geq \frac{A}{2}.\]
Theoretical Exercises
1.1 . The mean and variance of a linear function of a random variable . Let \(X\) be a random variable with finite mean and variance. Let \(a\) and \(b\) be real numbers. Show that
\begin{align} E[a X+b] & =a E[X]+b, & & \operatorname{Var}[a X+b]=|a|^{2} \operatorname{Var}[X], \\ \sigma[a X+b] & =|a| \sigma[X], & & \psi_{a X+b}(t)=e^{b t} \psi_{X}(a t) . \tag{1.24} \end{align}
1.2 . Chebyshev’s inequality for random variables . Let \(X\) be a random variable with finite mean and variance. Show that for any \(h>0\) and any \(\epsilon>0\)
\begin{align} & P\left[ |X-E[X]| \leq h \sigma[X] \right] \geq 1-\frac{1}{h^{2}}, \quad P\left[ |X-E[X]|>h\sigma[X] \right] \leq \frac{1}{h^{2}} \\ & P\left[ |X-E[X]| \leq \epsilon \right] \geq 1-\frac{\sigma^{2}[X]}{\epsilon^{2}}, \quad P\left[ |X-E[X]|>\epsilon \right] \leq \frac{\sigma^{2}[X]}{\epsilon^{2}} \tag{1.25} \end{align}
Hint : \(\quad P[|X-E[X]| \leq h \sigma[X]]=F_{X}(E[X]+h \sigma[X])-F_{X}(E[X]-h \sigma[X])\) if \(F_{X}(\cdot)\) is continuous at these points.
1.3 . Continuation of example 1E. Using (1.17), show that \(P[N<\infty]=1\) .
Exercises
1.1 . Consider a gambler who is to win 1 dollar if a 6 appears when a fair die is tossed; otherwise he wins nothing. Find the mean and variance of his winnings.
Answer
Mean, \(\frac{1}{6}\) ; variance, \(\frac{5}{36}\) .
1.2 . Suppose that 0.008 is the probability of death within a year of a man aged 35. Find the mean and variance of the number of deaths within a year among 20,000 men of this age.
1.3 . Consider a man who buys a lottery ticket in a lottery that sells 100 tickets and that gives 4 prizes of 200 dollars, 10 prizes of 100 dollars, and 20 prizes of 10 dollars. How much should the man be willing to pay for a ticket in this lottery?
Answer
Mean winnings, 20 dollars.
1.4 . Would you pay 1 dollar to buy a ticket in a lottery that sells \(1,000,000\) tickets and gives 1 prize of 100,000 dollars, 10 prizes of 10,000 dollars, and 100 prizes of 1000 dollars?
1.5 . Nine dimes and a silver dollar are in a red purse, and 10 dimes are in a black purse. Five coins are selected without replacement from the red purse and placed in the black purse. Then 5 coins are selected without replacement from the black purse and placed in the red purse. The amount of money in the red purse at the end of this experiment is a random variable. What is its mean and variance?
Answer
Mean, 1 dollar 60 cents; variance, 1800 cents \(^{2}\) .
1.6 . St.Petersburg problem (or paradox?) . How much would you be willing to pay to play the following game of chance. A fair coin is tossed by the player until heads appears. If heads appears on the first toss, the bank pays the player 1 dollar. If heads appears for the first time on the second throw the bank pays the player 2 dollars. If heads appears for the first time on the third throw the player receives \(4=2^{2}\) dollars. In general, if heads appears for the first time on the \(n\) th throw, the player receives \(2^{n-1}\) dollars. The amount of money the player will win in this game is a random variable; find its mean. Would you be willing to pay this amount to play the game? (For a discussion of this problem and why it is sometimes called a paradox see T. C. Fry, Probability and Its Engineering Uses , Van Nostrand, New York, 1928, pp. 194–199.)
1.7 . The output of a certain manufacturer (it may be radio tubes, textiles, canned goods, etc.) is graded into 5 grades, labeled \(A^{5}, A^{4}, A^{3}, A^{2}\) , and \(A\) (in decreasing order of quality). The manufacturer’s profit, denoted by \(X\) , on an item depends on the grade of the item, as indicated in the table. The grade of an item is random; however, the proportions of the manufacturer’s output in the various grades is known and is given in the table below. Find the mean and variance of \(X\) , in which \(X\) denotes the manufacturer’s profit on an item selected randomly from his production.
| Grade of an Item | Profit on an Item of This Grade | Probability that an Item Is of This Grade |
|---|---|---|
| \(A^{5}\) | \(\$ 1.00\) | \(\frac{5}{16}\) |
| \(A^{4}\) | \(0.80\) | \(\frac{1}{4}\) |
| \(A^{3}\) | \(0.60\) | \(\frac{1}{4}\) |
| \(A^{2}\) | \(0.00\) | \(\frac{1}{16}\) |
| \(A\) | \(-0.60\) | \(\frac{1}{8}\) |
Answer
Mean, 58.75 cents; variance, 26 cents \(^{2}\) .
1.8 . Consider a person who commutes to the city from a suburb by train. He is accustomed to leaving his home between 7:30 and 8:00 A.M. The drive to the railroad station takes between 20 and 30 minutes. Assume that the departure time and length of trip are independent random variables, each uniformly distributed over their respective intervals. There are 3 trains that he can take, which leave the station and arrive in the city precisely on time. The first train leaves at 8:05 A.M. and arrives at 8:40 A.M., the second leaves at 8:25 A.M. and arrives at 8:55 A.M., the third leaves at 9:00 A.M. and arrives at 9:43 A.M.
(i) Find the mean and variance of his time of arrival in the city.
(ii) Find the mean and yariance of his time of arrival under the assumption that he leaves his home between 7:30 and 7:55 A.M.
1.9 . Two athletic teams play a series of games; the first team to win 4 games is the winner. Suppose that one of the teams is stronger than the other and has probability \(p\) [equal to (i) 0.5, (ii) \(\frac{2}{3}\) ] of winning each game, independent of the outcomes of any other game. Assume that a game cannot end in a tie. Find the mean and variance of the number of games required to conclude the series. (Use exercise 3.26 of Chapter 3.)
Answer
(i) Mean, 5.81, variance, 1.03; (ii) mean, 5.50, variance, 1.11.
1.10 . Consider an experiment that consists of \(N\) players independently tossing fair coins. Let \(A\) be the event that there is an “odd” man (that is, either exactly one of the coins falls heads or exactly one of the coins falls tails). For \(r=1,2, \ldots\) let \(X_{r}\) be the number of times the experiment is repeated until the event occurs for the \(r\) th time.
(i) Find the mean and variance of \(X_{r}\) .
(ii) Evaluate \(E\left[X_{r}\right]\) and \(\operatorname{Var}\left[X_{r}\right]\) for \(N=3,4,5\) and \(r=1,2,3\) .
1.11 . Let an urn contain 5 balls, numbered 1 to 5. Let a sample of size 3 be drawn with replacement (without replacement) from the urn and let \(X\) be the largest number in the sample. Find the mean and variance of \(X\) .
Answer
With replacement, mean, 4.19, variance, 0.92; without replacement, mean, 4.5, variance 0.45.
1.12 . Let \(X\) be \(N\left(m, \sigma^{2}\right)\) . Find the mean and variance of (i) \(|X|\) , (ii) \(|X-c|\) where (a) \(c\) is a given constant, (b) \(\sigma=m=c=1,(c) \sigma=m=1, c=2\) .
1.13 . Let \(X\) and \(Y\) be independent random variables, each \(N(0,1)\) . Find the mean and variance of \(\sqrt{X^{2}+Y^{2}}\) .
Answer
Mean, \(\sqrt{\pi / 2}\) ; variance, \(2-(\pi / 2)\) .
1.14 . Find the mean and variance of a random variable \(X\) that obeys the probability law of Laplace, specified by the probability density function, for some constants \(\alpha\) and \(\beta>0\) :
\[f(x)=\frac{1}{2 \beta} \exp \left(-\frac{|x-\alpha|}{\beta}\right).\quad-\infty
1.15 . The velocity \(v\) of a molecule with mass \(m\) in a gas at absolute temperature \(T\) is a random variable obeying the Maxwell Boltzmann law:
\begin{align} f_{v}(x) & = \begin{cases} \displaystyle\frac{4}{\sqrt{\pi}} \beta^{3/2} x^{2} e^{-\beta x^{2}}, & \text{if } x > 0 \\ 0, & \text{if } x < 0, \end{cases} \end{align}
in which \(\beta=m /(2 k T), k=\) Boltzmann’s constant. Find the mean and variance of (i) the velocity of a molecule, (ii) the kinetic energy \(E=\frac{1}{2} m v^{2}\) of a molecule.
Answer
\(E\left[v^{n}\right]=\beta^{-n / 2} \frac{2}{\sqrt{\pi}} \Gamma\left(\frac{n+3}{2}\right)\) .
- At the end of the section we give an example that shows that (1.5) does not hold if the integrals used to define expectations are not required to converge absolutely. ↩︎
- The roulette table described is the one traditionally in use in most European casinos. The roulette tables in many American casinos have wheels that are divided into 38 arcs, bearing numbers \(00,0,1, \ldots, 36\) . ↩︎