Previously, we talked about principal stresses in plane stress problems. We learned that if \(\sigma_1\) and \(\sigma_2\) are the principal stresses in a 2D problem, there is no shear stress on their corresponding planes, and they are the maximum and minimum normal stresses.

In this section, we want to answer this question again: Does a plane exist on which the stress vector is purely normal, with no shear component? If such planes exist, we call their normal directions, the principal directions and the corresponding normal stresses, the principal stresses.

The Condition for Purely Normal Stress

Previously, we learned that the traction vector (also known as the stress vector) on an oblique plane whose unit normal vector is \(\mathbf{\hat{n}}\) can be calculated through \[ \mathbf{t}=\hat{\mathbf{n}}\boldsymbol{\sigma},\tag{1} \] where \(\boldsymbol{\sigma}\) is the stress tensor. Also in general, the stress vector can be decomposed into two components: a normal stress, \(\sigma_n\), acting perpendicular to the plane, and a shear stress, \(\tau_n\), acting parallel to the plane.

The normal stress \(\sigma_n\) is the projection of the traction vector onto the normal direction: \[ \sigma_n = \mathbf{t} \cdot \mathbf{\hat{n}}\tag{2} \] The shear component is the magnitude of the remaining part of the traction vector: \[ \tau_n = \sqrt{|\mathbf{t} - \sigma_n \mathbf{\hat{n}}|}=\sqrt{|\mathbf{t}|^2-\sigma_n^2}\tag{3} \] Our goal is to find a plane where the shear component is zero (\(\tau_n = 0\)). This condition is met if and only if the traction vector \(\mathbf{t}\) is parallel to the normal vector \(\mathbf{\hat{n}}\). Mathematically, this means the traction vector must be a scalar multiple of the normal vector: \[ \mathbf{t} = \sigma_n\mathbf{\hat{n}}\tag{4} \] Here, the scalar of proportionality, \(\sigma_n\), is the magnitude of the normal stress on that plane.

The Eigenvalue Problem Formulation

By substituting Eq. (1) into Eq. (4), we get: \[ \mathbf{\hat{n}}\boldsymbol{\sigma} = \sigma_n\mathbf{\hat{n}}\tag{5} \] This equation seeks a direction \(\mathbf{\hat{n}}\) for which the action of the stress tensor \(\boldsymbol{\sigma}\) results in a vector that is parallel to \(\mathbf{\hat{n}}\) itself.

For easier manipulation, we can take the transpose of this equation. Given that the stress tensor is symmetric (\(\boldsymbol{\sigma}^T = \boldsymbol{\sigma}\)), the previous equation becomes:1 \[ \boldsymbol{\sigma} \mathbf{n}^T = \sigma_n \mathbf{n}^T \] In matrix form, this is expressed as: \[ \begin{bmatrix} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{12} & \sigma_{22} & \sigma_{23} \\ \sigma_{13} & \sigma_{23} & \sigma_{33} \end{bmatrix} \begin{bmatrix} n_1 \\ n_2 \\ n_3 \end{bmatrix} = \sigma_n \begin{bmatrix} n_1 \\ n_2 \\ n_3 \end{bmatrix}\tag{6} \] This is a classic eigenvalue problem.2 We are looking for the eigenvalues \(\sigma_n\) and the corresponding eigenvectors \(\mathbf{n}\) of the stress tensor \(\boldsymbol{\sigma}\).

Solving for Principal Stresses and Directions

To find the values of \(\sigma_n\) for which a non-trivial solution for \(\mathbf{n}\) exists, we write the right hand side of (6) as \[ \sigma_n\begin{bmatrix} n_1 \\ n_2 \\ n_3 \end{bmatrix}=\sigma_n I\begin{bmatrix} n_1 \\ n_2 \\ n_3 \end{bmatrix}=\begin{bmatrix} \sigma_0 & 0 & 0\\ 0 & \sigma_n & 0\\ 0 & 0 & \sigma_n \end{bmatrix}\begin{bmatrix} n_1 \\ n_2 \\ n_3 \end{bmatrix}\tag{7} \] where \(I\) is the unit matrix. Then we rearrange the equation: \[ (\boldsymbol{\sigma} - \sigma_n I)\mathbf{n}^T = \mathbf{0}\tag{8} \] or equivalently \[ \begin{bmatrix} \sigma_{11}-\sigma_n & \sigma_{12} & \sigma_{13} \\ \sigma_{12} & \sigma_{22}-\sigma_n & \sigma_{23} \\ \sigma_{13} & \sigma_{23} & \sigma_{33}-\sigma_n \end{bmatrix} \begin{bmatrix} n_1 \\ n_2 \\ n_3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}\tag{9} \] A non-trivial solution for \(\mathbf{n}\) exists if and only if the determinant of the coefficient matrix is zero.3 \[ |\boldsymbol{\sigma} - \sigma_n I| = 0\tag{10} \] This leads to the characteristic equation: \[ \begin{vmatrix} \sigma_{11}-\sigma_n & \sigma_{12} & \sigma_{13} \\ \sigma_{12} & \sigma_{22}-\sigma_n & \sigma_{23} \\ \sigma_{13} & \sigma_{23} & \sigma_{33}-\sigma_n \end{vmatrix} = 0\tag{11} \] Expanding this determinant yields a cubic equation for \(\sigma_n\): \[ \sigma_n^3-I_1 \sigma_n^2-I_2\sigma_n-I_3=0,\tag{12} \] where 4 \[ \begin{aligned} I_1&=\sigma_{11}+\sigma_{22}+\sigma_{33}=\rm{tr}(\boldsymbol{\sigma})\\ I_2&=-\left|\begin{array}{ll}\sigma_{11} & \sigma_{12} \\ \sigma_{12} & \sigma_{22}\end{array}\right|-\left|\begin{array}{ll}\sigma_{11} & \sigma_{13} \\ \sigma_{13} & \sigma_{33}\end{array}\right|-\left|\begin{array}{ll}\sigma_{22} & \sigma_{22} \\ \sigma_{23} & \sigma_{33}\end{array}\right|\\ I_3&=\begin{vmatrix} \sigma_{11} & \sigma_{12} & \sigma_{13}\\ \sigma_{12} & \sigma_{22} & \sigma_{23}\\ \sigma_{13} & \sigma_{23} & \sigma_{33} \end{vmatrix}=\rm{det}(\boldsymbol{\sigma}). \end{aligned}\tag{13} \]

For any real symmetric matrix, all of its eigenvalues are real numbers. Therefore, equation (12) has three real solutions. The three roots of this equation, denoted as \(\sigma_1, \sigma_2\), and \(\sigma_3\), (\(\sigma_3\leq \sigma_2\leq \sigma_1\)) are the eigenvalues of the stress tensor. These specific values are known as the principal stresses.

For each principal stress (eigenvalue), we can solve the system of linear equations to find the corresponding eigenvector \(\mathbf{n}\). These vectors define the principal directions. The planes whose normal vectors align with these principal directions are called the principal planes.

From linear algebra we know that we have three different scenarios: 1. If the principal stresses are distinct, then the three principal directions are mutually orthogonal. A pure shear state is an example of this scenario. 2. We may have two principle stresses that are equal, but the third one is different. The pure tensile stress is an example of this scenario. In this case, the principal direction (eigenvector) corresponding to the distinct principal stress is normal to a plane. Any direction in that plane is a principal direction. Therefore, in this plane, we can choose two distinct directions such that with the normal of this plane form three mutually orthogonal directions 3. All principal stresses are equal. In this case every direction is a principal direction, and obviously we can three mutually orthogonal directions.

From these three scenarios, we learned that always we can find a cube (each face perpendicular to a principal direction) such that there is no shear stress on the faces of this cube.

Therefore, for any given state of stress, there exist three mutually perpendicular planes, known as principal planes, on which the shear stress component is zero. The stress acting on these planes is purely normal, and the magnitudes of these stresses are the principal stresses, which are found by solving the eigenvalue problem for the stress tensor.

How to Find Principal Stresses

Instead of forming the characteristic equation (12): \[ \sigma_n^3-I_1 \sigma_n^2-I_2\sigma_n-I_3=0 \] and attempting to solve it (for example, numerically), we can make use of mathematical software packages such as NumPy, MATLAB, Mathematica, or Wolfram Alpha. These tools are capable of find eigenvalues (principal stresses) and eigenvectors (principal directions) of a square matrix.

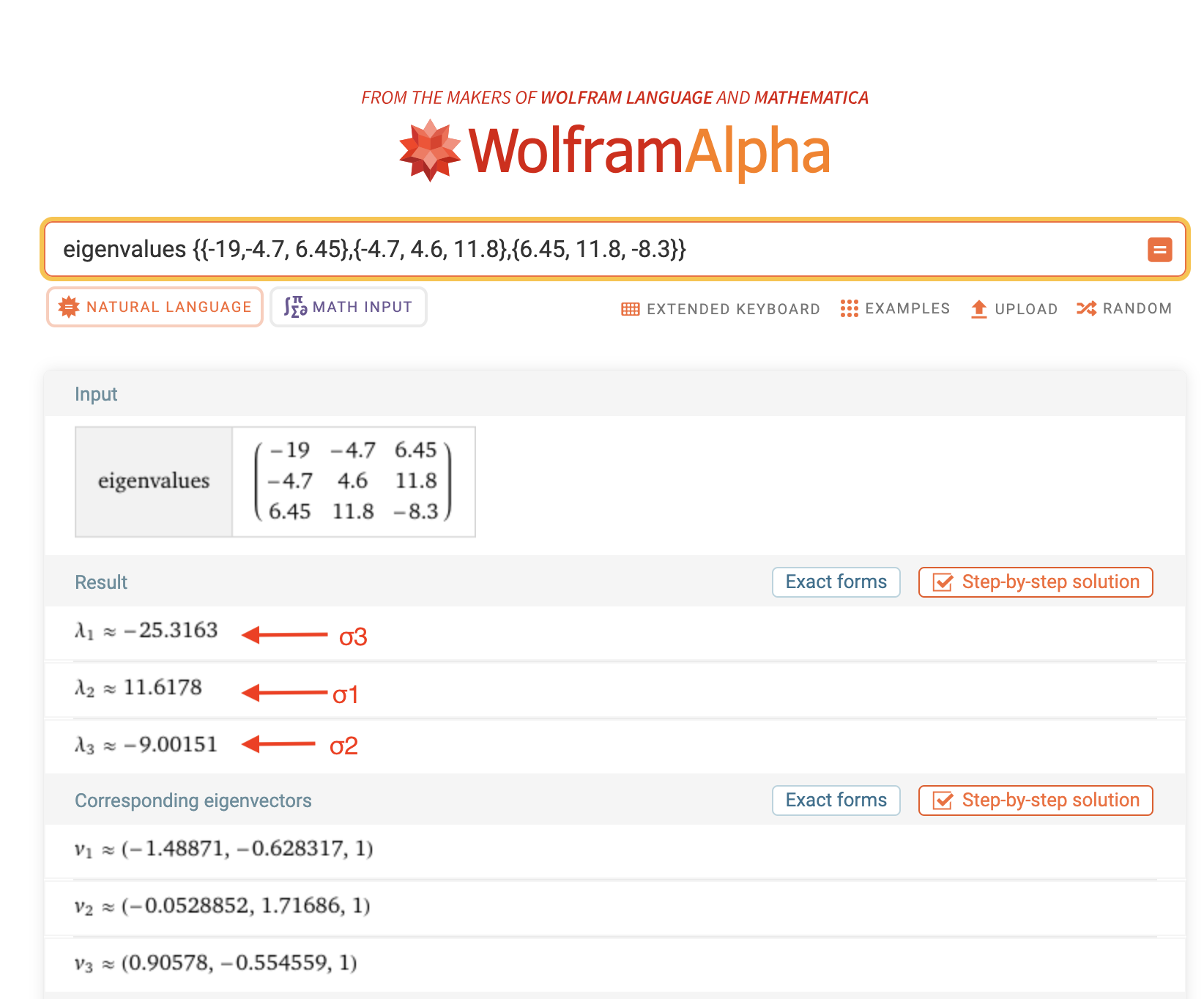
Wolfram Alpha can be used to determine the principal stresses.

Note that the eigenvectors returned by these programs are typically not unit vectors (i.e., their lengths are not equal to 1). If we need to find the direction cosines for a principal direction, we must normalize the corresponding eigenvector by dividing each of its components by the magnitude (length) of the vector.

Invarients of the Stress Tensor

The principal stresses are physical quantities, and their values are independent of the coordinate system in which the components of stress are given. That is, they are invariants of the stress state. No matter which coordinate system we choose, when we find the principal stresses (the eigenvalues of the stress tensor matrix), the values will remain the same.

Because the principal stresses are invariant, the coefficients of the characteristic equation used to find them must also be invariant with respect to any rotation of the coordinate system. The coefficients \(I_1\), \(I_2\), and \(I_3\) are called first, second, and third invarients of the stress tensor.

If we choose the principal directions as the new coordinate system, the stress looks like this: \[ \begin{bmatrix} \sigma_a & 0 & 0\\ 0 & \sigma_b & 0\\ 0 & 0 &\sigma_c \end{bmatrix} \] where, \(\sigma_b\), and \(\sigma_c\) are the principal stresses.5 And the invarients of the stress tensor will have simpler algebraic forms: \[ \begin{aligned} I_1&=\sigma_1+\sigma_2+\sigma_3\\ I_2&=-(\sigma_1\sigma_2+\sigma_2\sigma_3+\sigma_3\sigma_1)\\ I_3&=\sigma_1 \sigma_2 \sigma_3 \end{aligned} \]

Maximum and Minimum Normal Stress

If \(\sigma_1\), \(\sigma_2\), and \(\sigma_3\) (with \(\sigma_3\leq \sigma_2\leq \sigma_1\)) are three principal stresses, we can prove that the maximum normal stress that occurs on any plane is \(\sigma_1\) and the minimum normal stress is \(\sigma_3\).

Notice that in ordering, the sign has be taken into consideration, meaning that a compressive stress, which is considered negative, is considered smaller than a tensile stress, which is considered positive.

Proof of the fact that the maximum normal stress at a point equals the largest principal stress (eigenvalue) of the stress tensor.

1. Formulation as a Constrained Optimization Problem

The normal stress \(\sigma_n\) on a plane with a unit normal vector \(\mathbf{n}\) is the projection of the traction vector \(\mathbf{t}\) onto the direction of \(\mathbf{n}\). \[ \sigma_n = \mathbf{t} \cdot \mathbf{n} = (\mathbf{n}\boldsymbol{\sigma})\mathbf{n}^T = \mathbf{n}\boldsymbol{\sigma}\mathbf{n}^T \] We want to find the maximum and minimum of this function subject to the constraint that \(\mathbf{n}\) is a unit vector: \[ g(\mathbf{n}) = \mathbf{n}\mathbf{n}^T - 1 = 0 \]

2. Applying Lagrange Multipliers

We define the Lagrangian function \(L\), where \(\lambda\) is the Lagrange multiplier: \[ L(\mathbf{n}, \lambda) = \mathbf{n}\boldsymbol{\sigma}\mathbf{n}^T - \lambda(\mathbf{n}\mathbf{n}^T - 1) \] The stationary points occur when the gradient of \(L\) with respect to \(\mathbf{n}\) is the zero vector. The gradient of the quadratic form \(\mathbf{n}\boldsymbol{\sigma}\mathbf{n}^T\) is \(2\mathbf{n}\boldsymbol{\sigma}\) (since \(\boldsymbol{\sigma}\) is symmetric), and the gradient of \(\mathbf{n}\mathbf{n}^T\) is \(2\mathbf{n}\). \[ \nabla_{\mathbf{n}} L = 2\mathbf{n}\boldsymbol{\sigma} - 2\lambda\mathbf{n} = \mathbf{0} \] This simplifies to the left eigenvalue equation: \[ \mathbf{n}\boldsymbol{\sigma} = \lambda\mathbf{n} \]

3. Interpretation and Conclusion

This result shows that the normal stress attains its extreme values only when the normal vector \(\mathbf{n}\) is a (left) eigenvector of the stress tensor \(\boldsymbol{\sigma}\). These directions are the principal directions. The stress on principal planes (perpendicular to the principal directions) are a principal stress.

Why do we care about the maximum normal stress?

Brittle materials fail by tensile stress. For example, a piece of chalk under bending breaks on a plane perpendicular to its long axis because the tensile stress is along this axis. However, in torsion, the chalk breaks on surface that makes 45 degrees with its axial direction, as the maximum tensile stress occurs at 45 degrees

Maximum Shear Stress

We can prove that the maximum shear stress is \[ \tau_{\max}=\frac{\sigma_1-\sigma_3}{2}. \] The maximum shear stress occurs on a plane whose the normal vector makes 45 degrees with the principal directions corresponding to \(\sigma_1\) and \(\sigma_2\) (see the following figure).

Maximum shear stress occurs on planes whose normal vectors make 45 degrees with the principal directions (shaded planes)
Proof of the fact that the maximum shear stress at a point equals half the difference between the largest and smallest eigenvalues.

Step 1: Expressing Shear Stress in the Principal Coordinate System

The analysis is greatly simplified in a coordinate system aligned with the principal directions. In this basis, the stress tensor \(\boldsymbol{\sigma}\) is a diagonal matrix of the principal stresses \(\sigma_1, \sigma_2, \sigma_3\). We assume the ordering \(\sigma_1 \ge \sigma_2 \ge \sigma_3\). \[ \boldsymbol{\sigma} = \begin{bmatrix} \sigma_1 & 0 & 0 \\ 0 & \sigma_2 & 0 \\ 0 & 0 & \sigma_3 \end{bmatrix} \] The shear stress squared is given by \(\tau_n^2 = |\mathbf{t}|^2 - \sigma_n^2\). Let’s express these terms:

  • \(|\mathbf{t}|^2 = \mathbf{t}\mathbf{t}^T = (\mathbf{n}\boldsymbol{\sigma})(\mathbf{n}\boldsymbol{\sigma})^T = (\mathbf{n}\boldsymbol{\sigma})(\boldsymbol{\sigma}^T \mathbf{n}^T) = \mathbf{n}\boldsymbol{\sigma}^2\mathbf{n}^T\) since \(\boldsymbol{\sigma}\) is symmetric and diagonal. This gives \(|\mathbf{t}|^2 = n_1^2\sigma_1^2 + n_2^2\sigma_2^2 + n_3^2\sigma_3^2\).
  • \(\sigma_n^2 = (\mathbf{n}\boldsymbol{\sigma}\mathbf{n}^T)^2 = (n_1^2\sigma_1 + n_2^2\sigma_2 + n_3^2\sigma_3)^2\).

Our function to maximize is: \[ \tau_n^2 = (n_1^2\sigma_1^2 + n_2^2\sigma_2^2 + n_3^2\sigma_3^2) - (n_1^2\sigma_1 + n_2^2\sigma_2 + n_3^2\sigma_3)^2 \] subject to the constraint \(n_1^2 + n_2^2 + n_3^2 = 1\).

Step 2: Detailed Lagrange Multiplier Analysis for Shear Stress

We want to find the stationary points of \(\tau_n^2\). We form the Lagrangian function \(L\), with multiplier \(\mu\): \[ L(n_1, n_2, n_3, \mu) = \tau_n^2 - \mu(n_1^2 + n_2^2 + n_3^2 - 1) \] We find the partial derivative with respect to each \(n_k\) and set it to zero. For \(n_1\): \[ \frac{\partial L}{\partial n_1} = \frac{\partial (\tau_n^2)}{\partial n_1} - 2\mu n_1 = 0 \] The derivative of \(\tau_n^2\) is: \[ \frac{\partial (\tau_n^2)}{\partial n_1} = (2n_1\sigma_1^2) - 2(n_1^2\sigma_1 + n_2^2\sigma_2 + n_3^2\sigma_3)(2n_1\sigma_1) = 2n_1\sigma_1^2 - 4n_1\sigma_1\sigma_n \] Setting the derivative of \(L\) to zero gives: \[ 2n_1\sigma_1^2 - 4n_1\sigma_1\sigma_n - 2\mu n_1 = 0 \quad \implies \quad n_1(\sigma_1^2 - 2\sigma_1\sigma_n - \mu) = 0 \] By symmetry, we obtain a system of three equations: 1. \(n_1(\sigma_1^2 - 2\sigma_1\sigma_n - \mu) = 0\) 2. \(n_2(\sigma_2^2 - 2\sigma_2\sigma_n - \mu) = 0\) 3. \(n_3(\sigma_3^2 - 2\sigma_3\sigma_n - \mu) = 0\)

We analyze the possible solutions for \(\mathbf{n}\):

  • Case A: Two components of \(\mathbf{n}\) are zero. Let \(n_1=1, n_2=0, n_3=0\). This is a principal direction. Here \(\sigma_n = \sigma_1\) and \(|\mathbf{t}|^2 = \sigma_1^2\), so \(\tau_n^2 = \sigma_1^2 - \sigma_1^2 = 0\). These are the points of minimum shear stress.

  • Case B: One component of \(\mathbf{n}\) is zero. Let \(n_3 = 0\), and assume \(n_1 \neq 0\) and \(n_2 \neq 0\). For the system of equations to hold, the terms in the parentheses for the first two equations must be zero: \[ \begin{aligned} \sigma_1^2 - 2\sigma_1\sigma_n = \mu \\ \sigma_2^2 - 2\sigma_2\sigma_n = \mu \end{aligned} \] Equating these expressions for \(\mu\) gives: \[ \sigma_1^2 - 2\sigma_1\sigma_n = \sigma_2^2 - 2\sigma_2\sigma_n \] \[ \sigma_1^2 - \sigma_2^2 = 2\sigma_n(\sigma_1 - \sigma_2) \] Factoring the left side: \[ (\sigma_1 - \sigma_2)(\sigma_1 + \sigma_2) = 2\sigma_n(\sigma_1 - \sigma_2) \] Assuming \(\sigma_1 \neq \sigma_2\), we can divide by \((\sigma_1 - \sigma_2)\) to find the value of the normal stress at this stationary point: \[ \sigma_n = \frac{\sigma_1 + \sigma_2}{2} \] Now we use this to find the values of \(n_1^2\) and \(n_2^2\). We have two equations:

    1. from the definition of \(\sigma_n\): \(\sigma_n = n_1^2\sigma_1 + n_2^2\sigma_2 = \frac{\sigma_1 + \sigma_2}{2}\)
    2. from the unit vector constraint: \(n_1^2 + n_2^2 = 1\)

    Substitute \(n_2^2 = 1 - n_1^2\) from (ii) into (i): \[ n_1^2\sigma_1 + (1 - n_1^2)\sigma_2 = \frac{\sigma_1 + \sigma_2}{2} \] \[ n_1^2\sigma_1 + \sigma_2 - n_1^2\sigma_2 = \frac{\sigma_1}{2} + \frac{\sigma_2}{2} \]\[ n_1^2(\sigma_1 - \sigma_2) = \frac{\sigma_1}{2} - \frac{\sigma_2}{2} = \frac{\sigma_1 - \sigma_2}{2} \] Again, assuming \(\sigma_1 \neq \sigma_2\), we find \(n_1^2 = 1/2\). From the constraint, it follows that \(n_2^2 = 1/2\). This corresponds to a plane whose normal bisects the angle between the principal axes 1 and 2.

Step 3: Calculating the Shear Stress at the Stationary Points

Now we calculate the value of \(\tau_n^2\) at this stationary point (\(n_1^2=1/2, n_2^2=1/2, n_3^2=0\)): \[ \tau_n^2 = |\mathbf{t}|^2 - \sigma_n^2 \] \[ \tau_n^2 = \left(\frac{1}{2}\sigma_1^2 + \frac{1}{2}\sigma_2^2\right) - \left(\frac{\sigma_1 + \sigma_2}{2}\right)^2 \] Putting everything over a common denominator of 4: \[ \tau_n^2 = \frac{2\sigma_1^2 + 2\sigma_2^2}{4} - \frac{(\sigma_1^2 + 2\sigma_1\sigma_2 + \sigma_2^2)}{4} \] \[ \tau_n^2 = \frac{2\sigma_1^2 + 2\sigma_2^2 - \sigma_1^2 - 2\sigma_1\sigma_2 - \sigma_2^2}{4} \] \[ \tau_n^2 = \frac{\sigma_1^2 - 2\sigma_1\sigma_2 + \sigma_2^2}{4} = \left(\frac{\sigma_1 - \sigma_2}{2}\right)^2 \] The shear stress at this point is \(\tau_n = \left| \frac{\sigma_1 - \sigma_2}{2} \right|\).

Step 4: Identifying the Maximum Value

The same analysis can be applied to the other pairs of principal planes, yielding three stationary values for the shear stress:

  1. \(\tau_{12} = \left| \frac{\sigma_1 - \sigma_2}{2} \right|\) (on planes bisecting axes 1 and 2)
  2. \(\tau_{23} = \left| \frac{\sigma_2 - \sigma_3}{2} \right|\) (on planes bisecting axes 2 and 3)
  3. \(\tau_{13} = \left| \frac{\sigma_1 - \sigma_3}{2} \right|\) (on planes bisecting axes 1 and 3)

The absolute maximum shear stress, \(\tau_{max}\), must be the largest of these three values. Given our ordering \(\sigma_1 \ge \sigma_2 \ge \sigma_3\), the largest difference between any two principal stresses is \((\sigma_1 - \sigma_3)\).

Therefore, the maximum shear stress is: \[ \tau_{\max} = \frac{\sigma_1 - \sigma_3}{2} \]

Why do we care about the maximum shear stress?

Ductile materials such as most metals fail by plastic yielding which often occurs on a plane with maximum shear stress.

Application of Mohr’s Circle for 3D Analysis of Stress

We just showed that there are always three principal directions. If we keep one of them fixed and rotate the other two direction around this fixed one, we can analyze the transformation using Mohr’s circle. Let the principal directions 1, 2, and 3 correspond to the principal stresses \(\sigma_1\), \(\sigma_2\), and \(\sigma_3\), respectively, ordered such that \(\sigma_1 \ge \sigma_2 \ge \sigma_3\).

The largest of these circles is the one generated by rotating around the intermediate principal direction (direction 2), as it spans between the maximum and minimum principal stresses (see the following figure).

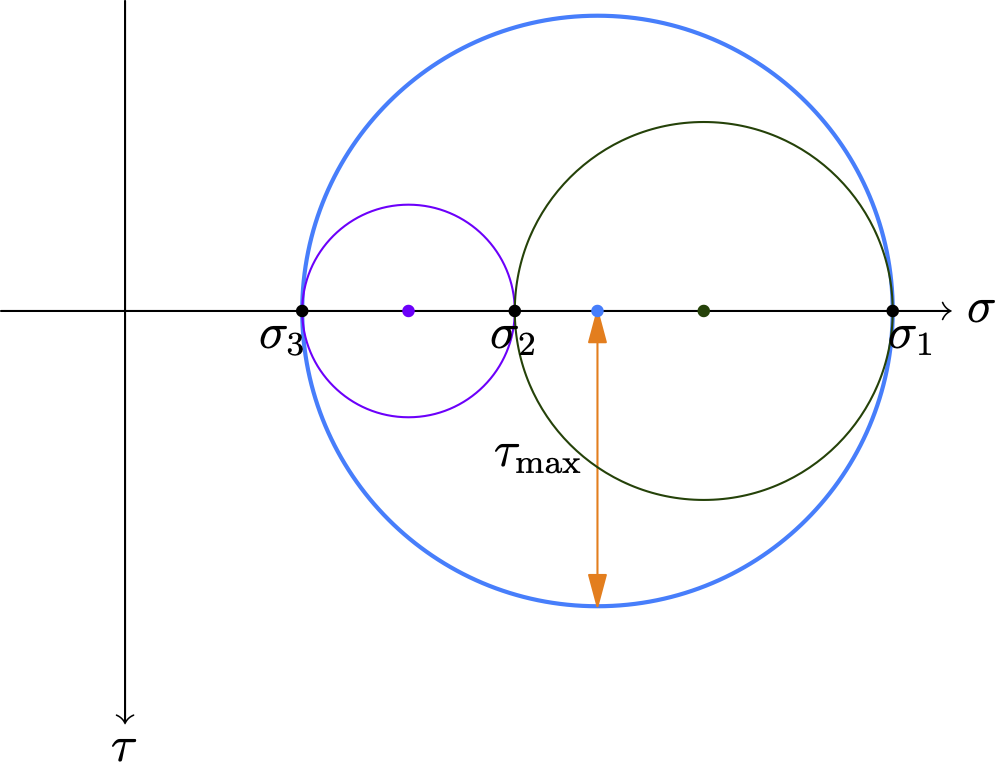
Mohr’s circle for 3D stress analysis

From this graphical representation, it is clear that the absolute maximum shear stress, \(\tau_{\max}\), is equal to the radius of this largest circle. \[ \tau_{\max} = \frac{\sigma_1 - \sigma_3}{2} \] Also, from the figure, it is clear that the normal to the plane of maximum shear stress is oriented at 45 degrees to principal directions 1 and 3 (Recall that a rotation of θ on the physical stress element corresponds to a rotation of 2θ in the same direction on Mohr’s Circle).

  1. If A and B are two matrices, then \((AB)^T=B^T A^T\) where the superscript T denotes the transpose of the matrix.↩︎
  2. Let A be a square vector. We say the nonzero vector \(\mathbf{v}\) is an eigenvector of A, if there is a real or complex number \(\lambda\) such that \(A\mathbf{v}=\lambda\mathbf{v}\). In other words, the linear transformation represented by matrix A maps the eigenvector \(\mathbf{v}\) onto a vector that is parallel to itself. The scalar \(\lambda\) iss called the eigenvalue corresponding to the eigenvector \(\mathbf{v}\).↩︎
  3. The equation \(A\mathbf{x}=\mathbf{y}\) where A is a square matrix and \(\mathbf{x}\) and \(\mathbf{y}\) are two column vectors has a unique solution if and only if A has an inverse \(A^{-1}\) . In this case the unique solution is given by \(\mathbf{x}=A^{-1}\mathbf{y}\).↩︎
  4. If A is a square matrix, the sum of the elements on its main diagonal (from the upper left to the lower right) is called the trace of the matrix and denoted by tr(A).↩︎
  5. We did not use \(\sigma_1\), \(\sigma_2\), and \(\sigma_3\), because depending on which principal direction is selected as the first direction, \(\sigma_a\) can be any of these values (not necessarily the largest one).↩︎