To find the traction vector \(\mathbf{t}^{(\hat{\mathbf{n}})}\) on an arbitrary plane with unit normal \(\hat{\mathbf{n}}=n_x\hat{\mathbf{i}}+n_y\hat{\mathbf{j}}+n_z\hat{\mathbf{z}}\), we analyze the equilibrium of an infinitesimal tetrahedron. The face with area \(\Delta S\) is the oblique face, and its projections onto the coordinate planes have areas \(\Delta S_x\), \(\Delta S_y\), and \(\Delta S_z\).

Since the tetrahedron is in static equilibrium, the sum of all forces must be equal to zero. Balacing Balancing the forces in the x-direction gives: \[ t_x \Delta S = \sigma_{xx}\Delta S_x + \sigma_{yx}\Delta S_y + \sigma_{zx}\Delta S_z + \rho b_x\Delta V \] Here, the term \(t_x \Delta S\) is the force on the oblique face, the \(\sigma\) terms are the forces on the coordinate faces, and \(\rho b_x\Delta V\) is the body force.

We can use two key geometric relationships:

  1. The areas of the coordinate faces are projections of the oblique face: \[ \Delta S_x = n_x\Delta S,\quad \Delta S_y = n_y\Delta S,\quad \Delta S_z = n_z\Delta S. \]
  2. The volume of a tetrahedron is \(\Delta V = \frac{1}{3}h\Delta S\), where \(h\) is the perpendicular height from the point \(P\) to the oblique face.

Substituting these into the force balance and dividing by \(\Delta S\), we get: \[ t_x = \sigma_{xx}n_x + \sigma_{yx}n_y + \sigma_{zx}n_z + \rho b_x h \]

To find the traction vector at the point \(P\), we let the dimensions of the tetrahedron shrink. In this limit, the height \(h\) approaches zero, causing the body force term to vanish. This leaves us with the x-component of the traction vector: \[ t_x = \sigma_{xx}n_x + \sigma_{yx}n_y + \sigma_{zx}n_z \]

By applying the same logic to the y and z directions, we obtain the other components: \[ \begin{aligned} t_y &= \sigma_{xy}n_x + \sigma_{yy}n_y + \sigma_{zy}n_z \\ t_z &= \sigma_{xz}n_x + \sigma_{yz}n_y + \sigma_{zz}n_z \end{aligned} \] This set of equations is known as Cauchy’s Stress Formula. In matrix notation, treating the traction and normal vectors as row vectors, this relationship is written as: \[ \begin{bmatrix} t_x & t_y & t_z \end{bmatrix}=\begin{bmatrix} n_x & n_y & n_z \end{bmatrix} \begin{bmatrix}\sigma_{xx} & \sigma_{xy} & \sigma_{xz}\\\sigma_{yx} &\sigma_{yy} & \sigma_{yz}\\\sigma_{zx} & \sigma_{zy} & \sigma_{zz}\end{bmatrix} \quad \text{or} \quad \mathbf{t} = \hat{\mathbf{n}} \boldsymbol{\sigma} \]

As discussed before, the traction vector (also known as the stress) can be resolved into two components: (1) a normal stress component and (2) a shear stress component.

A sectioned body in a 3D coordinate system shows the traction vector t(n) at point P. This vector is broken down into its normal component, sigma_n, perpendicular to the surface, and its shear component, tau_n, parallel to the surface, illustrating that the traction vector is the sum of these two stress components.
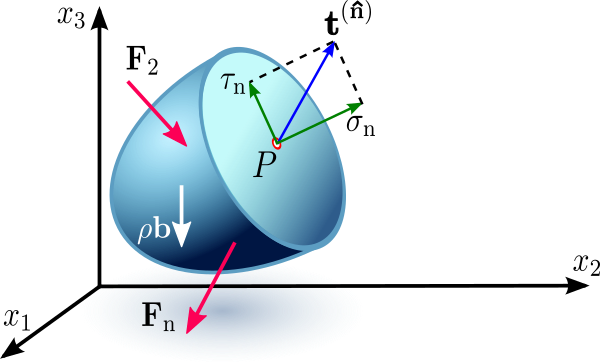
The traction vector (also known as stress vector) t(n) at a point P on an internal surface is decomposed into two components: a normal stress component σn, which acts perpendicular to the surface, and a shear stress component τn, which acts parallel to the surface.

From the above figure, it is clear that \[ \sigma_n= \mathbf{t}^{(\hat{\mathbf{n}})} \cdot\hat{\mathbf{n}} \] and thus \[ \tau_n=|\mathbf{t}^{(\hat{\mathbf{n}})}-\sigma_n\hat{\mathbf{n}}| \]

Example1 A material particle is in a state of stress with the following components: \[ \boldsymbol{\sigma} = \begin{bmatrix} 1 & 2 & 5 \\ 2 & 3 & 6 \\ 5 & 6 & 4 \end{bmatrix} \]

  1. Compute the traction vector on a plane intersecting the axes x, y, z at 1, 2, and 3, respectively.
  2. Compute the magnitude of the normal stress on the plane.
  3. Compute the magnitude of the shear stress on the plane.
  4. Compute the direction of the shear stress on the plane.
Solution

We first find the unit vector normal to the plane.

The equation of a plane intersecting the axes at x=1, y=2, z=3 is: \[ \frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1 \] This plane is normal to the vector: \[ \mathbf{n} \propto \begin{bmatrix} \frac{1}{1} & \frac{1}{2}& \frac{1}{3} \end{bmatrix} \]

Normalizing: \[ \mathbf{n} = \frac{1}{\sqrt{(1)^2 + (1/2)^2 + (1/3)^2}} \begin{bmatrix} 1 & \tfrac{1}{2} & \tfrac{1}{3} \end{bmatrix} = \begin{bmatrix} 6/7 & 3/7 & 2/7 \end{bmatrix} \]

(a) Traction vector on the plane

The traction vector is: \[ \mathbf{t} = \hat{\mathbf{n}} \boldsymbol{\sigma} = \begin{bmatrix} 6/7 & 3/7 & 2/7 \end{bmatrix}\begin{bmatrix} 1 & 2 & 5 \\ 2 & 3 & 6 \\ 5 & 6 & 4 \end{bmatrix} = \begin{bmatrix} 22/7 & 33/7 & 56/7 \end{bmatrix} \]

(b) Normal stress on the plane

The normal stress is the projection of \(\mathbf{t}\) onto \(\mathbf{n}\):

\[ \sigma_n = \mathbf{t} \cdot \hat{\mathbf{n}} = \frac{22}{7}\cdot \frac{6}{7} + \frac{33}{7}\cdot \frac{3}{7} + \frac{56}{7}\cdot \frac{2}{7} = 7 \]

(c) and (d) Shear stress vector and its magnitude

The shear stress vector is the component of \(\mathbf{t}\) tangent to the plane:

\[ \boldsymbol{\tau} = \mathbf{t} - \sigma_n \mathbf{n} \] \[ \boldsymbol{\tau} = \begin{bmatrix} 22/7 & 33/7 & 56/7 \end{bmatrix} - 7 \begin{bmatrix} 6/7 & 3/7 & 2/7 \end{bmatrix} = \frac{1}{7} \begin{bmatrix} -20 & 12 & 42 \end{bmatrix} \]

The magnitude is: \[ |\boldsymbol{\tau}| = \sqrt{\left(-\frac{20}{7}\right)^2 + \left(\frac{12}{7}\right)^2 + \left(\frac{42}{7}\right)^2} = 6.86 \]

The direction is: \[ \hat{\boldsymbol{\tau}} = \frac{\boldsymbol{\tau}}{|\boldsymbol{\tau}|} = \frac{1}{\sqrt{(-20)^2 + 12^2 + 42^2}} \begin{bmatrix} -20 \\ 12 \\ 42 \end{bmatrix} \]

✅ Final Results

  • Traction vector: \(\mathbf{t} = \left(\tfrac{22}{7}, \tfrac{33}{7}, \tfrac{56}{7}\right)\)
  • Normal stress: \(\sigma_n = 7\)
  • Shear stress magnitude: \(|\boldsymbol{\tau}| = 6.86\)
  • Shear stress direction: along \([-20, 12, 42]\)
  1. This example is from Prof. Suo’s lecture notes for ES240 in Harvard University with minor adaptation.↩︎