In the next two sections we discuss an example that illustrates the need to introduce various concepts concerning random variables, which will, in turn, be presented in the course of the discussion. We begin in this section by discussing the example in terms of the notion of a numerical valued random phenomenon in order to show the similarities and differences between this notion and that of a random variable.

Let us consider a commuter who is in the habit of taking a train to the city; the time of departure from the station is given in the railroad timetable as 7:55 A.M. However, the commuter notices that the actual time of departure is a random phenomenon, varying between 7:55 and 8 A.M. Let us assume that the probability law of the random phenomenon is specified by a probability density function \(f_{1}(\cdot)\) ; further, let us assume

\begin{align} f_{1}\left(x_{1}\right) &= \begin{cases} \frac{2}{25}\left(5-x_{1}\right), & \text{for } 0 \leq x_{1} \leq 5 \tag{3.1}\\ 0, & \text{otherwise.} \end{cases} \end{align} 

in which \(x_{1}\) represents the number of minutes after 7:55 A.M. that the train departs.

Let us suppose next that the time it takes the commuter to travel from his home to the station is a numerical valued random phenomenon, varying between 25 and 30 minutes. Then, if the commuter leaves his home at 7:30 A.M. every day, his time of arrival at the station is a random phenomenon, varying between 7:55 and 8 A.M. Let us suppose that the probability law of this random phenomenon is specified by a probability density function \(f_{2}(\cdot)\) ; further, let us assume that \(f_{2}(\cdot)\) is of the same functional form as \(f_{1}(\cdot)\) , so that \begin{align} f_{2}\left(x_{2}\right) &= \begin{cases} \frac{2}{25}\left(5-x_{2}\right), & \text{for } 0 \leq x_{2} \leq 5 \tag{3.2}\\ 0, & \text{otherwise,} \end{cases} \end{align} in which \(x_{2}\) represents the number of minutes after 7:55 A.M. that the commuter arrives at the station.

The question now naturally arises: will the commuter catch the 7:55 A.M. train? Of course, this question cannot be answered by us; but perhaps we can answer the question: what is the probability that fhe commuter will catch the 7:55 A.M. train?

Before any attempt can be made to answer this question, we must express mathematically as a set on a sample description space the random event described verbally as the event that the commuter catches the train. Further, to compute the probability of the event, a probability function on the sample description space must be defined.

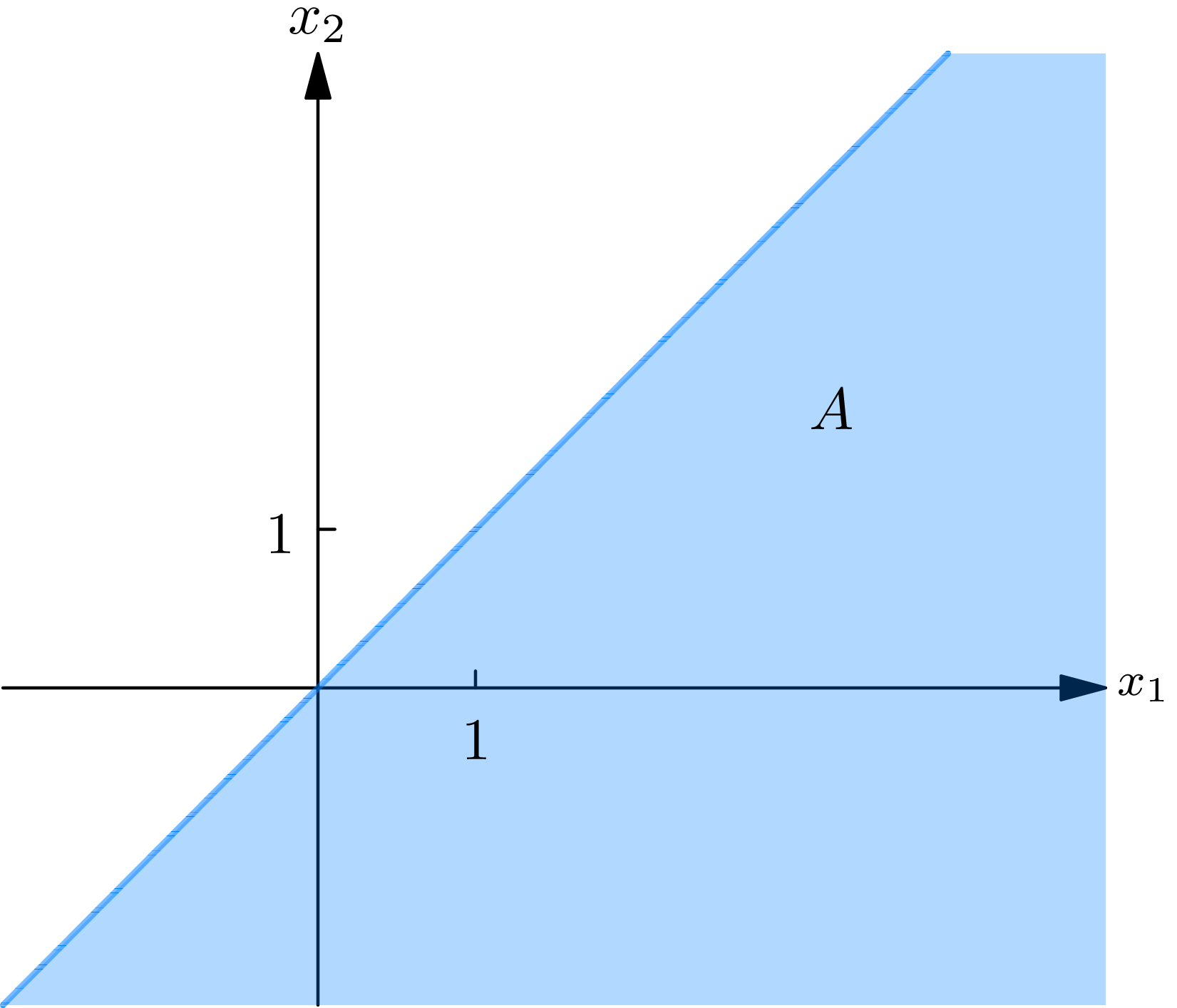
As our sample description space \(S\) , we take the space of 2-tuples \(\left(x_{1}, x_{2}\right)\) of real numbers, where \(x_{1}\) represents the time (in minutes after 7:55 A.M.) at which the train departs from the station, and \(x_{2}\) denotes the time (in minutes after 7:55 A.M.) at which the commuter arrives at the station. The event \(A\) that the man catches the train is then given as a set of sample descriptions by \(A=\left\{\left(x_{1}, x_{2}\right): x_{1}>x_{2}\right\}\) , since to catch the train his arrival time \(x_{2}\) must be less than the train’s departure time \(x_{1}\) . The event \(A\) is diagrammed in Fig. 3A .

We define next a probability function \(P[\cdot]\) on the events in \(S\) . To do this, we use the considerations of section 7 , Chapter 4, concerning numerical 2-tuple valued random phenomena. In particular, let us suppose that the probability function \(P[\cdot]\) is specified by a 2-dimensional probability density function \(f(.,.)\) . From a knowledge of \(f(.,.)\) we may compute the probability \(P[A]\) that the commuter will catch his train by the formula

\begin{align} P[A] & =\iint_{A} f\left(x_{1}, x_{2}\right) d x_{1} d x_{2} \tag{3.3}\\ & =\int_{-\infty}^{\infty} d x_{1} \int_{-\infty}^{x_{1}} d x_{2} f\left(x_{1}, x_{2}\right) \\ & =\int_{-\infty}^{\infty} d x_{2} \int_{x_{2}}^{\infty} d x_{1} f\left(x_{1}, x_{2}\right) \end{align} 

in which the second and third equations follow by the usual rules of calculus for evaluating double integrals (or integrals over the plane) by means of iterated (or repeated) single integrals.

We next determine whether the function \(f(.,.)\) is specified by our having specified the probability density functions \(f_{1} (\cdot)\) and \(f_{2} (\cdot)\) by (3.1) and (3.2) .

More generally, we consider the question: what relationship exists between the individual probability density functions \(f_{1} (\cdot)\) and \(f_{2} (\cdot)\) and the joint probability density function \(f (.,.)\) ? We show first that from a knowledge of \(f (.,.)\) , one may obtain a knowledge of \(f_{1} (\cdot)\) and \(f_{2} (\cdot)\) by the formulas, for all real numbers \(x_{1}\) and \(x_{2}\) , \begin{align} & f_{1}\left(x_{1}\right)=\int_{-\infty}^{\infty} f\left(x_{1}, x_{2}\right) d x_{2} \\ & f_{2}\left(x_{2}\right)=\int_{-\infty}^{\infty} f\left(x_{1}, x_{2}\right) d x_{1}. \end{aligned} \tag{3.4}\] 

Conversely, we show by a general example that from a knowledge of \(f_{1} (\cdot)\) and \(f_{2} (\cdot)\) one cannot obtain a knowledge of \(f (.,.)\) , since \(f (.,.)\) is not uniquely determined by \(f_{1} (\cdot)\) and \(f_{2} (\cdot)\) ; more precisely, we show that to given probability density functions \(f_{1} (\cdot)\) and \(f_{2} (\cdot)\) there exists an infinity of functions \(f (.,.)\) that satisfy (3.4) with respect to \(f_{1} (\cdot)\) and \(f_{2} (\cdot)\) .

To prove (3.4), let \(F_{1}(\cdot)\) and \(F_{2}(\cdot)\) be the distribution functions of the first and second random phenomena under consideration; in the example discussed, \(F_{1}(\cdot)\) is the distribution function of the departure time of the train from the station, and \(F_{2}(\cdot)\) is the distribution function of the arrival time of the man at the station. We may obtain expressions for \(F_{1}(\cdot)\) and \(F_{2}(\cdot)\) in terms of \(f(.,.)\) , for \(F_{1}(x)\) is equal to the probability, according to the probability function \(P[\cdot]\) , of the set \(\left\{\left(x_{1}^{\prime}, x_{2}^{\prime}\right): x_{1}^{\prime} \leq x_{1},-\infty, and similarly \(F_{2}\left(x_{2}\right)=P\left[\left\{\left(x_{1}^{\prime}, x_{2}^{\prime}\right):-\infty. Consequently,

\begin{align} & F_{1}\left(x_{1}\right)=\int_{-\infty}^{x_{1}} d x_{1}^{\prime} \int_{-\infty}^{\infty} d x_{2}^{\prime} f\left(x_{1}^{\prime}, x_{2}^{\prime}\right) \tag{3.5}\\ & F_{2}\left(x_{2}\right)=\int_{-\infty}^{x_{2}} d x_{2}^{\prime} \int_{-\infty}^{\infty} d x_{1}^{\prime} f\left(x_{1}^{\prime}, x_{2}^{\prime}\right) \end{align} 

We next use the fact that

\[f_{1}\left(x_{1}\right)=\frac{d}{d x_{1}} F_{1}\left(x_{1}\right), \quad f_{2}\left(x_{2}\right)=\frac{d}{d x_{2}} F_{2}\left(x_{2}\right). \tag{3.6}\] 

By differentiation of (3.5), in view of (3.6), we obtain (3.4).

Conversely, given any two probability density functions \(f_{1}(\cdot)\) and \(f_{2}(\cdot)\) , let us show how one may find many probability density functions \(f(.,.)\) to satisfy (3.4). Let \(A\) be a positive number. Choose a finite nonempty interval \(a_{1}\) to \(b_{1}\) such that \(f_{1}\left(x_{1}\right) \geq A\) for \(a_{1} \leq x_{1} \leq b_{1}\) . Similarly, choose a finite nonempty interval \(a_{2}\) to \(b_{2}\) such that \(f_{2}\left(x_{2}\right) \geq A\) for \(a_{2} \leq x_{2} \leq b_{2}\) . Define a function of two variables \(h(.,.)\) by

\[h\left(x_{1}, x_{2}\right) =\left\{ \begin{aligned} &A^{2} \sin \left[\frac{\pi}{b_{1}-a_{1}}\left(x_{1}-\frac{a_{1}+b_{1}}{2}\right)\right] \sin \left[\frac{\pi}{b_{2}-a_{2}}\left(x_{2}-\frac{a_{2}+b_{2}}{2}\right)\right],\\ &\qquad \qquad \text{if both } a_{1} \leq x_{1} \leq b_{1} \text{ and } a_{2} \leq x_{2} \leq b_{2} \\ &0, \qquad \text{otherwise.} \end{aligned}\right. \tag{3.7}\] 

Clearly, by construction, for all \(x_{1}\) and \(x_{2}\) 

\begin{align} & \left|h\left(x_{1}, x_{2}\right)\right| \leq f_{1}\left(x_{1}\right) f_{2}\left(x_{2}\right), \tag{3.8}\\ & \int_{-\infty}^{\infty} h\left(x_{1}, x_{2}\right) d x_{1}=\int_{-\infty}^{\infty} h\left(x_{1}, x_{2}\right) d x_{2}=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} h\left(x_{1}, x_{2}\right) d x_{1} d x_{2}=0. \end{align} 

Define the function \(f(.,.)\) for any real numbers \(x_{1}\) and \(x_{2}\) by

\[f\left(x_{1}, x_{2}\right)=f_{1}\left(x_{1}\right) f_{2}\left(x_{2}\right)+h\left(x_{1}, x_{2}\right). \tag{3.9}\] 

It may be verified, in view of (3.8), that \(f(.,.)\) is a probability density function satisfying (3.4).

We now return to the question of how to determine \(f(.,.)\) . There is one (and, in general, only one) circuinstance in which the individual probability density functions \(f_{1}(\cdot)\) and \(f_{2}(\cdot)\) determine the joint probability density function \(f(.,.)\) , namely, when the respective random phenomena, whose probability density functions are \(f_{1}(\cdot)\) and \(f_{2}(\cdot)\) , are independent. 

We define two random phenomena as independent, letting \(P_{1}[\cdot]\) and \(P_{2}[\cdot]\) denote their respective probability functions and \(P[\cdot]\) their joint probability function, if it holds that for all real numbers \(a_{1}, b_{1}, a_{2}\) , and \(b_{2}\) 

\begin{align} P\left[\left\{\left(x_{1}, x_{2}\right):\right.\right. & \left.\left.a_{1}

Equivalently, two random phenomena are independent, letting \(F_{1}(\cdot)\) and \(F_{2}(\cdot)\) denote their respective distribution functions and \(F(.,.)\) their joint distribution function, if it holds that for all real numbers \(x_{1}\) and \(x_{2}\) 

\[F\left(x_{1}, x_{2}\right)=F_{1}\left(x_{1}\right) F_{2}\left(x_{2}\right). \tag{3.11}\] 

Equivalently, two continuous random phenomena are independent, letting \(f_{1}(\cdot)\) and \(f_{2} (\cdot)\) denote their respective probability density functions and \(f (.,.)\) their joint probability density, if it holds that for all real numbers \(x_{1}\) and \(x_{2}\) 

\[f\left(x_{1}, x_{2}\right)=f_{1}\left(x_{1}\right) f_{2}\left(x_{2}\right). \tag{3.12}\] 

Equivalently, two discrete random phenomena are independent, letting \(p_{1}(\cdot)\) and \(p_{2}(\cdot)\) denote their respective probability mass functions and \(p(.,.)\) their joint probability mass function if it holds that for all real numbers \(x_{1}\) and \(x_{2}\) 

\[p\left(x_{1}, x_{2}\right)=p_{1}\left(x_{1}\right) p_{2}\left(x_{2}\right). \tag{3.13}\] 

The equivalence of the foregoing statements concerning independence may be shown more or less with ease by using the relationships developed in Chapter 4; indications of the proofs are contained in section 6.

Independence may also be defined in terms of the notion of an event depending on a phenomenon , which is analogous to the notion of an event depending on a trial developed in section 2 of Chapter 3. An event \(A\) is said to depend on a random phenomenon if a knowledge of the outcome of the phenomenon suffices to determine whether or not the event \(A\) has occurred . We then define two random phenomena as independent if, for any two events \(A_{1}\) and \(A_{2}\) , depending, respectively, on the first and second phenomenon, the probability of the intersection of \(A_{1}\) and \(A_{2}\) is equal to the product of their probabilities:

\[P\left[A_{1} A_{2}\right]=P\left[A_{1}\right] P\left[A_{2}\right]. \tag{3.14}\] 

As shown in section 2 of Chapter 3, two random phenomena are independent if and only if a knowledge of the outcome of one of the phenomena does not affect the probability of any event depending upon the other phenomenon.

Let us now return to the problem of the commuter catching his train, and let us assume that the commuter’s arrival time and the train’s departure time are independent random phenomena. Then (3.12) holds, and from (3.3) 

\begin{align} P[A] & =\int_{-\infty}^{\infty} d x_{1} f_{1}\left(x_{1}\right) \int_{-\infty}^{x_{1}} d x_{2} f_{2}\left(x_{2}\right) \tag{3.15}\\ & =\int_{-\infty}^{\infty} d x_{2} f_{2}\left(x_{2}\right) \int_{x_{2}}^{\infty} d x_{1} f_{1}\left(x_{1}\right). \tag{3.14} \end{align} 

Since \(f_{1}(\cdot)\) and \(f_{2}(\cdot)\) are specified by (5.1) and (5.2) , respectively, the probability \(P[A]\) that the commuter will catch his train can now be computed by evaluating the integrals in (3.15) . However, in the present example there is a very special feature present that makes it possible to evaluate \(P[A]\) without any laborious calculation.

The reader may have noticed that the probability density functions \(f_{1}(\cdot)\) and \(f_{2}(\cdot)\) have the same functional form. If we define \(f(\cdot)\) by \(f(x)=\frac{-2}{25}(5-x)\) or 0, depending on whether \(0 \leq x \leq 5\) or otherwise, we find that \(f_{1}(x)=f_{2}(x)=f(x)\) for all real numbers \(x\) . In terms of \(f^{\prime}(\cdot)\) , we may write (3.15), making the change of variable \(x_{1}^{\prime}=x_{2}\) and \(x_{2}^{\prime}=x_{1}\) in the second integral, \begin{align} P[A] & =\int_{-\infty}^{\infty} d x_{1} f\left(x_{1}\right) \int_{-\infty}^{x_{3}} d x_{2} f\left(x_{2}\right) \tag{3.16}\\ & =\int_{-\infty}^{\infty} d x_{1}^{\prime} f\left(x_{1}^{\prime}\right) \int_{x_{1}^{\prime}}^{\infty} d x_{2}^{\prime} f\left(x_{2}^{\prime}\right). \end{align} 

By adding the two integrals in (3.16), it follows that \[2 P[A]=\int_{-\infty}^{\infty} d x_{1} f\left(x_{1}\right) \int_{-\infty}^{\infty} d x_{2} f\left(x_{2}\right)=1.\] 

We conclude that the probability \(P[A]\) that the man will catch his train is equal to \(\frac{1}{2}\) .

Exercises