In many cases the result of a random experiment is not expressed by a single quantity but by a family of simultaneously observed quantities. Thus, to describe the outcome of the tossing of a pair of distinguishable dice, one requires a 2-tuple \(\left(x_{1}, x_{2}\right)\) , in which \(x_{1}\) denotes the number obtained on the first die and \(x_{2}\) denotes the number obtained on the second die. Similarly, to describe the geographical location of an object (such as a ship), one requires a 2-tuple \(\left(x_{1}, x_{2}\right)\) , whose components represent the latitude and longitude of the ship, respectively. One may want to describe the prices of some commodity (such as wheat or International Business Machines’ common stock) on the first day of each month of a given year; to do this, one requires a 12-tuple \(\left(x_{1}, x_{2}, \ldots, x_{12}\right)\) whose components \(x_{1}, x_{2}, \ldots, x_{12}\) represent the price on the first day of January, February, March,…, November, and December, respectively. On the other hand, for some integer \(n\) one may want to describe the price of each of \(n\) commodities on a list (bread, milk, meats, shoes, electricity, etc.) on July 1 of a given year; to do this, one requires an \(n\) -tuple \(\left(x_{1}, x_{2}, \ldots, x_{n}\right)\) , whose components \(x_{1}, x_{2}, \ldots, x_{n}\) represent the price on July 1 of the first commodity on the list, the second commodity on the list, and so on, up to the \(n\) th commodity on the list.

We are thus led to the notion of a numerical \(n\) -tuple valued random phenomenon , which we define as a random phenomenon whose sample description space is the set \(R_{n}\) consisting of all \(n\) -tuples \(\left(x_{1}, x_{2}, \ldots, x_{n}\right)\) in which the components \(x_{1}, x_{2}, \ldots, x_{n}\) are real numbers from \(-\infty\) to \(\infty\) . In this section we indicate the notation that is used to discuss numerical \(n\) -tuple valued random phenomena. We begin by considering the case of \(n=2\) .

A numerical 2-tuple valued random phenomenon is described by stating its probability function \(P[\cdot]\) , whose value \(P[B]\) at any set \(B\) of 2-tuples of real numbers represents the probability that an observed occurrence of the random phenomenon will have a description lying in the set \(B\) . It is useful to think of the probability function \(P[\cdot]\) as representing a distribution of a unit mass of some substance, which we call probability, over a 2-dimensional plane on which rectangular coordinates have been marked off, as in Fig. 7A . For any (probabilizable) set \(B\) of 2 -tuples \(P[B]\) states the weight of the probability substance distributed over the set \(B\) .

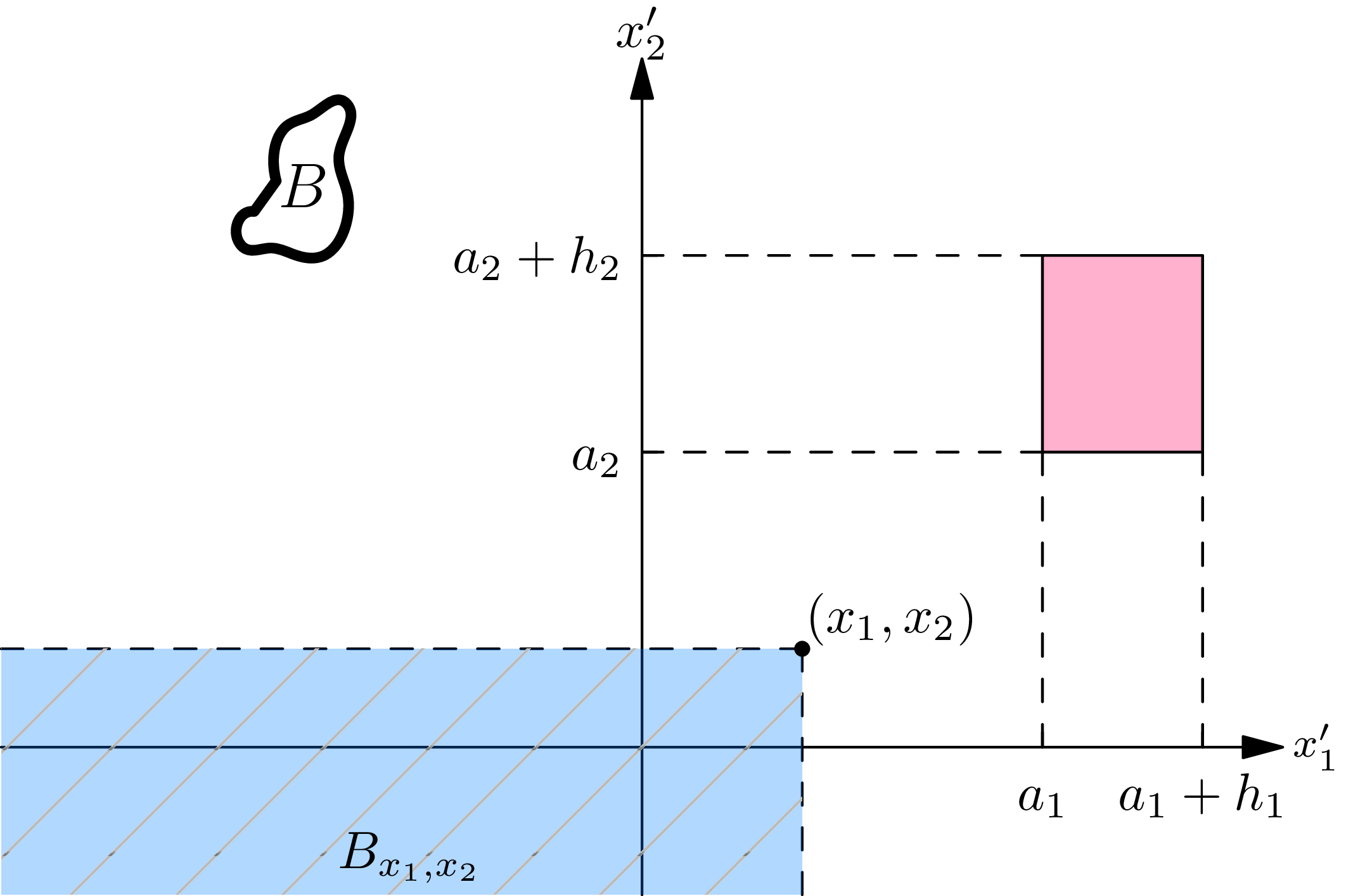
In order to know for all (probabilizable) sets \(B\) of 2-tuples the value \(P[B]\) of the probability function \(P[\cdot]\) of a numerical 2 -tuple valued random phenomenon, it suffices to know it for all real numbers \(x_{1}\) and \(x_{2}\) for the sets

\[B_{x_{1}, x_{2}}=\left\{2 \text {-tuples }\left(x_{1}^{\prime}, x_{2}^{\prime}\right): x_{1}^{\prime} \leq x_{1}, x_{2}^{\prime} \leq x_{2}\right\} \text {. } \tag{7.1}\] 

In words, \(B_{x_{1}, x_{2}}\) is the set consisting of all 2-tuples \(\left(x_{1}^{\prime}, x_{2}^{\prime}\right)\) whose first component \(x_{1}^{\prime}\) is less than the specified real number \(x_{1}\) and whose second component \(x_{2}^{\prime}\) is less than the specified real number \(x_{2}\) . We are thus led to introduce the distribution function \(F(., .)\) of the numerical 2-tuple valued random phenomenon, which is a function of two variables, defined for all real numbers \(x_{1}\) and \(x_{2}\) by the equation \[F\left(x_{1}, x_{2}\right)=P\left[B_{x_{1}, x_{2}}\right]. \tag{7.2}\] The quantity \(F\left(x_{1}, x_{2}\right)\) represents the probability that an observed occurrence of the random phenomenon under consideration will have as its description a 2-tuple whose first component is less than or equal to \(x_{1}\) and whose second component is less than or equal to \(x_{2}\) . In terms of the unit mass of probability distributed over the plane of Fig. 7A , \(F\left(x_{1}, x_{2}\right)\) is equal to the weight of the probability substance lying over the “infinitely extended rectangle”. which consists of all 2-tuples \(\left(x_{1}^{\prime}, x_{2}^{\prime}\right)\) , such that \(x_{1}^{\prime} \leq x_{1}\) and \(x_{2}^{\prime} \leq x_{2}\) , which corresponds to the shaded area in Fig. 7A .

The probability assigned to any rectangle in the plane may also be expressed in terms of the distribution function \(F(.,.)\) : for any real numbers \(a_{1}\) and \(a_{2}\) and any positive numbers \(h_{1}\) and \(h_{2}\) 

\begin{align} & P\left[\left\{\left(x_{1}^{\prime}, x_{2}^{\prime}\right): a_{1}

As in the case of numerical valued random phenomena, the most important cases of numerical 2-tuple valued random phenomena are those in which the probability function is specified either by a probability mass function or a probability density function.

Given a numerical 2-tuple valued random phenomenon, we define its probability mass function , denoted by \(p(.,.)\) , as a function of two variables; defined for all real numbers \(x_{1}\) and \(x_{2}\) by the equation \[p\left(x_{1}, x_{2}\right)=P\left[\left\{\left(x_{1}^{\prime}, x_{2}^{\prime}\right): \quad x_{1}^{\prime}=x_{1}, x_{2}^{\prime}=x_{2}\right\}\right] . \tag{7.4}\] 

The quantity \(p\left(x_{1}, x_{2}\right)\) represents the probability that an observed occurrence of the random phenomenon under consideration will have as its description a 2-tuple whose first component is equal to \(x_{1}\) and whose second component is equal to \(x_{2}\) . It may be shown that there is only a finite or countably infinite number of points at which \(p\left(x_{1}, x_{2}\right)>0\) .

We define a numerical 2-tuple valued random phenomenon as obeying a discrete probability law if the sum of its probability mass function, over the points \(\left(x_{1}, x_{2}\right)\) where \(p\left(x_{1}, x_{2}\right)>0\) , is equal to 1. Equivalently, the random phenomenon obeys a discrete probability law if its probability function \(P[\cdot]\) is specified by its probability mass function \(p(\cdot,\cdot)\) by the formula for any set \(B\) of 2-tuples:

\[P[B]=\sum_{\substack{\text { over }\left(x_{1}, x_{2}\right) \text { lying in } B \\ \text { such that } p\left(x_{1}, x_{2}\right)>0}} p\left(x_{1}, x_{2}\right). \tag{7.5}\] 

In terms of the unit of probability mass distributed over the plane of Fig. 7A by the probability function \(P[\cdot]\) , a numerical 2 -tuple valued random phenomenon obeys a discrete probability law if in order to distribute the corresponding unit probability mass one needs only attach a positive probability mass at each of a finite or countably infinite number of points.

We next consider numerical 2-tuple valued random phenomena whose probability functions \(P[\cdot]\) may be specified in terms of a function \(f(\cdot,\cdot)\) of two variables, which we call its probability density function. For every (probabilizable) set \(B\) of 2-tuples

\[P[B]=\iint_{B} f\left(x_{1}, x_{2}\right) d x_{1} d x_{2}. \tag{7.6}\] 

Equivalently, its distribution function \(F(\cdot,\cdot)\) satisfies, for every pair of real numbers \(x_{1}\) and \(x_{2}\) 

\[F\left(x_{1}, x_{2}\right)=\int_{-\infty}^{x_{1}} \int_{-\infty}^{x_{2}} f\left(x_{1}^{\prime}, x_{2}^{\prime}\right) d x_{1}^{\prime} d x_{2}^{\prime}. \tag{7.7}\] 

Consequently, the probability density function may be obtained from the distribution function \(F(.,.)\) by differentiation:

\[f\left(x_{1}, x_{2}\right)=\frac{\partial^{2}}{\partial x_{1} \partial x_{2}} F\left(x_{1}, x_{2}\right) \tag{7.8}\] 

at all 2-tuples \(\left(x_{1}, x_{2}\right)\) , where the second-order mixed partial derivative \(\partial^{2} /\left(\partial x_{1} \partial x_{2}\right) F\left(x_{1}, x_{2}\right)\) exists.

In the case of numerical 2-tuple valued random phenomena it remains true, from a practical point of view , that the only random phenomena whose distribution functions \(F(.,.)\) are continuous, regarded as a function of two variables, are those whose distribution functions are specified by a probability density function. Consequently, we shall say that a numerical 2-tuple valued random phenomenon obeys a continuous probability law if its probability function and distribution function are specified by a probability density function.

All the notions of this section extend immediately to numerical \(n\) -tuple valued random phenomena by reading \(n\) -tuple for 2 -tuple and \(\left(x_{1}, x_{2}, \ldots, x_{n}\right)\) for \(\left(x_{1}, x_{2}\right)\) in the foregoing discussion. In place of (7.1) to (7.8) read the following equations: \begin{align} & B_{x_{1}, x_{2}, \ldots, x_{n}} \tag{7.1$^\prime$} \\ & =\left\{n \text {-tuples }\left(x_{1}^{\prime}, x_{2}^{\prime}, \ldots, x_{n}^{\prime}\right): \quad x_{1}^{\prime} \leq x_{1}, x_{2}^{\prime} \leq x_{2}, \ldots, x_{n}^{\prime} \leq x_{n}\right\}. \end{align} \begin{align} F\left(x_{1}, x_{2}, \ldots, x_{n}\right)=P\left[B_{x_{1}, x_{2}}, \ldots, x_{n}\right] \tag{7.2$^\prime$}. \end{align} \begin{align} P & \left[\left\{\left(x_1^{\prime}, x_2^{\prime}, \ldots, x_n^{\prime}\right): \quad a_10}} p\left(x_1, x_2, \ldots, x_n\right) \tag{7.5$^\prime$}\] \[P[B]=\iint \cdots \int_B f\left(x_1, x_2, \ldots, x_n\right) d x_1 d x_2 \cdots d x_n \tag{7.6$^\prime$}\] \[F\left(x_1, x_2, \ldots, x_n\right) =\int_{-\infty}^{x_1} \int_{-\infty}^{x_2} \cdots \int_{-\infty}^{x_n} f\left(x_1^{\prime}, x_2^{\prime}, \ldots, x_n^{\prime}\right) d x_1^{\prime} d x_2^{\prime} \cdots d x_n^{\prime}. \tag{7.7$^\prime$}\] \[f\left(x_1, x_2, \ldots, x_n\right)=\frac{\partial^n}{\partial x_1 \partial x_2 \cdots \partial x_n} F\left(x_1, x_2, \ldots, x_n\right)\tag{7.8$^\prime$}\] 

There are many other notions that arise in connection with numerical \(n\) -tuple valued random phenomena, but they are best formulated in terms of random variables and consequently are discussed in Chapter 7 .

Exercises