An equation such as \(y=\frac{x^{2}}{2}+1\) connects two variables: \(x\) and \(y\) . We say an ordered pair satisfy the equation if it makes the equation true when the values for \(x\) and \(y\) are substituted into the equation. For example, \((0,1)\) , \((-1,1.5)\) , \((1,1.5)\) , \((2.1,3.205)\) , \(\ldots\) satisfy the given equation. There are infinite number of ordered pairs that satisfy such an equation.
The graph of an equation between \(x\) and \(y\) (or any other two variables) is the set of all points \((x,y)\) satisfying the equation. The phrase “plot the graph of an equation” or “sketch the graph of an equation” means to draw enough number of points and connect them by a smooth curve to illustrate the main features of the graph. Graphs of some equations are sketched below.
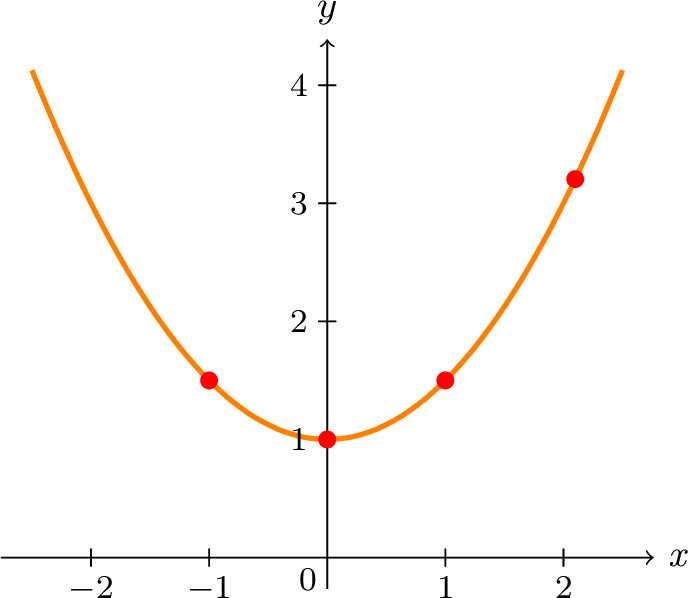 |
| (a) Graph of \(y=\frac{1}{2}x^{2}+1\) |
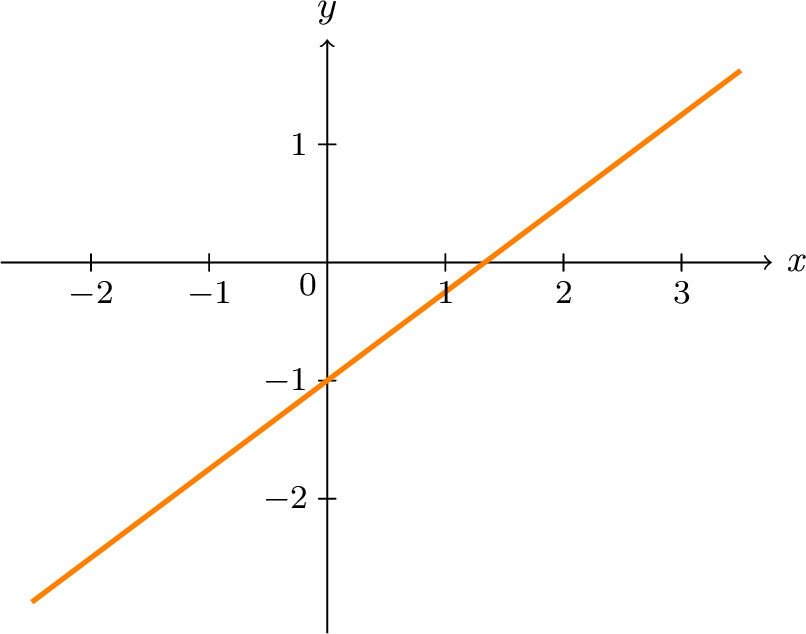 |
| (b) Graph of \(y=\frac{3}{4}x-1\) |
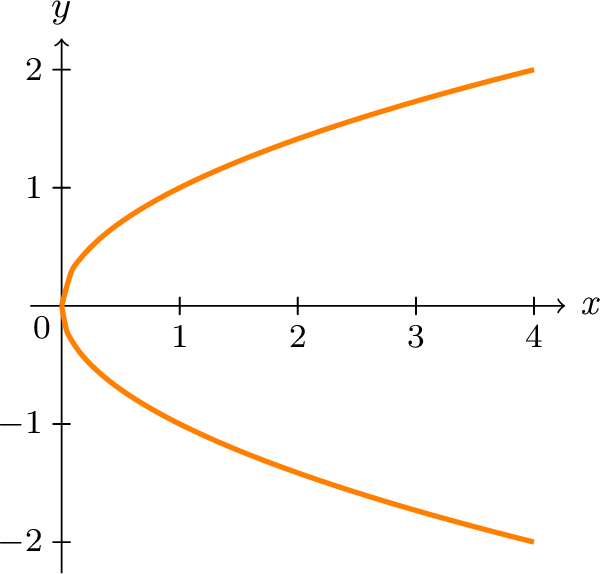 |
| (c) Graph of \(y^{2}=x\) |
Circles
Now let’s find the equation of a circle with radius \(r\) and center \(C(a,b)\) . By definition, this circle is the set of all points \(P(x,y)\) in a plane that are at a distance \(R\ge0\) from the point \(C(a,b)\) (see the following figure). From the Distance Formula we have \[|PC|=\sqrt{(x-a)^{2}+(y-b)^{2}}=R.\] By squaring both sides, we obtain: \[(x-a)^{2}+(y-b)^{2}=R^{2}\]
The standard form of the equation of a circle with radius \(R\) and center \((a,b)\) is \[(x-a)^{2}+(y-b)^{2}=R^{2}\]
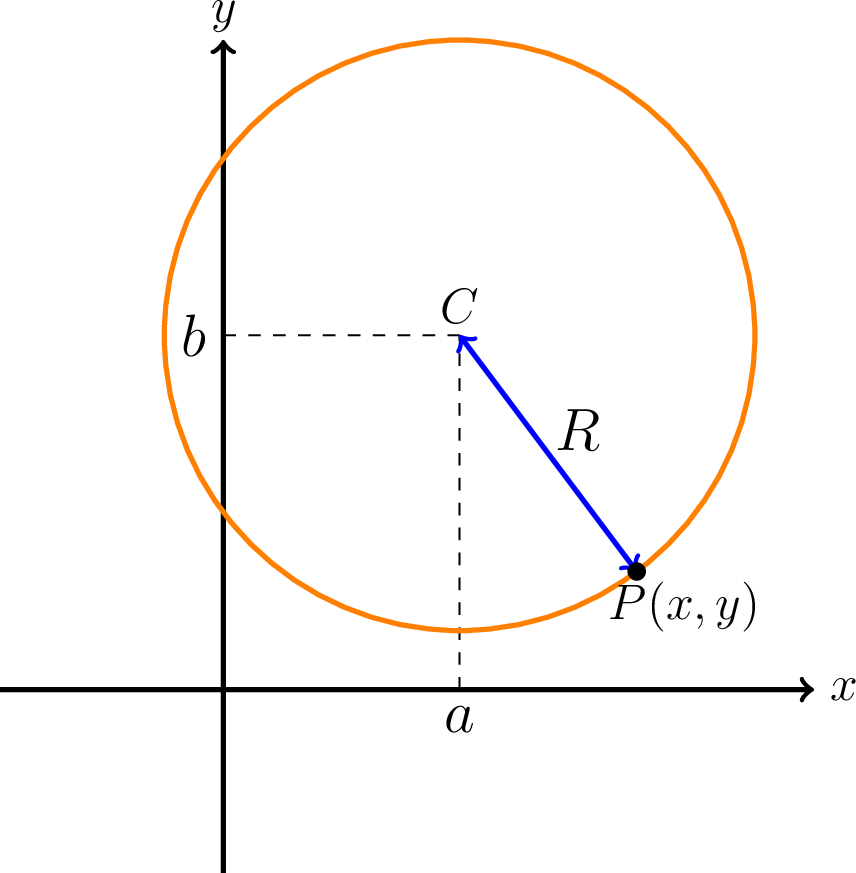
Example 1. Write an equation of the circle that has center \(C(-1,1)\) and contains the point \(P(-4,5)\) .
Solution
Because \(P\) is on the circle, the radius \(R\) is \(|PC|\) (also denoted by \(d(P,C)\) ). By the Distance formula , we have \[R=|PC|=\sqrt{(-4-(-1))^{2}+(5-1)^{2}}=\sqrt{25}=5.\] Substituting \(a=-1,b=2\) , and \(R=5\) in the equation of a circle gives us \[(x+1)^{2}+(y-1)^{2}=25.\] This circle is illustrated below.
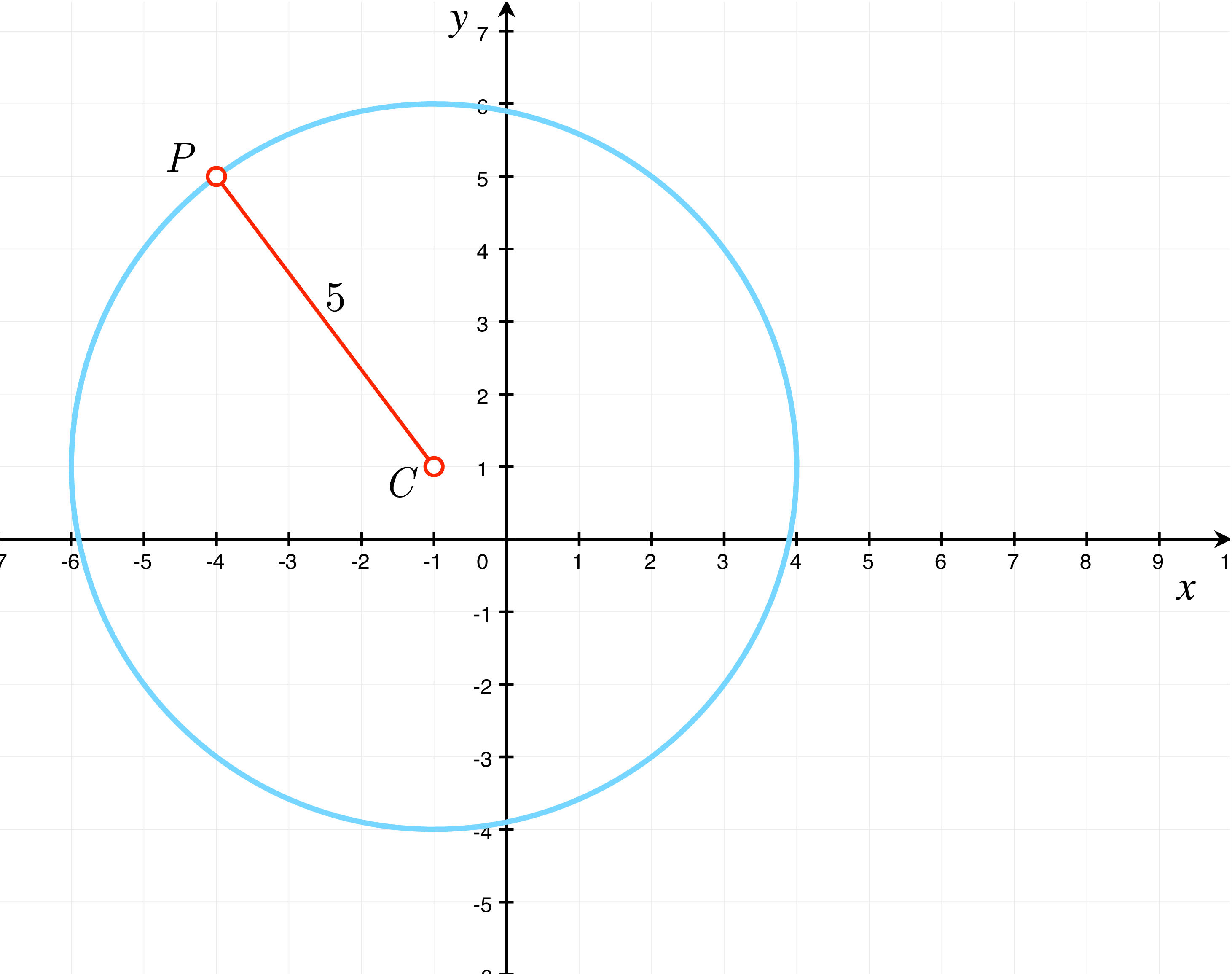
The standard form of the equation of a circle with radius 2 and center \((2,-3)\) is \[(x-2)^{2}+(y+3)^{2}=4.\] We can change the look of this equation by expanding the terms on the left hand side (using the formula for the Square of a Sum in Section: Special Products ): \[x^{2}-4x+4+y^{2}+6y+9=4\] \[x^{2}+y^{2}-4x+6x+13=4\] Subtracting 4 from both sides, the equation of the circle becomes \[x^{2}+y^{2}-4x+6x+9=0.\] The above equation is called the general form of the equation of the circle.
The general form of the equation of a circle is \[x^{2}+y^{2}+Ax+By+E=0.\] where \[\left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-E>0.\]
Read on to understand why the condition \(\left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-E>0\) is necessary.
Finding the Center and Radius of a Circle from Its Expanded Form
If we are given the equation of a circle in expanded form and want to find its center and radius, we need to rewrite the equation in the standard form: \[(x - a)^2 + (y - b)^2 = R^2,\] where \((a, b)\) is the center and \(r\) is the radius. This involves a process called completing the square . Here’s how it works:
Steps
- Group the terms : Separate the \(x\) - and \(y\) -terms, moving the constant to the other side: \[x^2 + y^2 + Ax + By + E = 0 \quad \Rightarrow \quad (x^2 + Ax) + (y^2 + By) = -E\]
- Complete the square :
- For the \(x\) -terms, take half the coefficient of \(x\) (from \(Ax\) ), square it, and add it inside the parentheses: \((A/2)^2\) . \[x+Ax=x+Ax\color{red}{+\left(\frac{A}{2}\right)^2-\left(\frac{A}{2}\right)^2}=\left(x+\frac{A}{2}\right)^2\color{red}{-\left(\frac{A}{2}\right)^2}\]
- Do the same for the \(y\) -terms with \(B\) : \((B/2)^2\) .
- Add these same values to the right-hand side of the equation to keep it balanced.
- Rewrite the equation : After completing the square, the equation will look like: \[(x + A/2)^2 + (y + B/2)^2 = R^2\]
- Identify the center and radius :
- The center is \((-A/2, -B/2)\) .
- The radius is \(\sqrt{R^2}\) , or the square root of the value on the right-hand side.
Example 2. Find the center and radius of the circle with equation \[x^{2}+y^{2}-12x+14y+69=0.\]
Solution
To easily find the center and the radius of the circle, we need to rewrite the equation of the circle in the form \[(x-a)^{2}+(y-b)^{2}=R^{2}.\] In doing so, on the left side, we group the terms containing \(x\) together, and the terms containing \(y\) together, and move the constant to the right side by subtracting \(69\) from both sides: \[(x^{2}-12x)+(y^2+14y)=-69.\] Then we complete the square for each variable (do not forget to add the required constants for completing the squares on both sides of the equations). \[\left[x^2-12x+\left(-\frac{12}{2}\right)^{2}\right]-6^{2}+\left[y^2+14x+\left(\frac{14}{2}\right)^{2}\right]-7^{2} =-69\] \[\begin{align} (x-6)^{2}+(y+7)^{2} & =-69+36+49\tag{add $6^2$ and $7^2$ to both sides}\\ (x-6)^{2}+(y+7)^{2} & =16\\ (x-6)^2+(y-(-7))^{2} & =4^{2} \end{align}\] Comparing the above equation with the standard form of the equation of a circle reveals that the center is \((6,-7)\) and the radius is 4.
Example 3. Identifying the Equation of a Circle.
Show that the equation \(x^2 + y^2 + 4x - 6y + 9 = 0\) represents a circle and find the center and radius.
Solution
We first group the \(x\) - and \(y\) -terms and add \(-9\) to both sides to have the constant only on the right-hand side: \[(x^2 + 4x) + (y^2 - 6y) = -9\]
Next, complete the square for each group:
- For \(x^2 + 4x\) , add \(\left(\frac{4}{2}\right)^2 = 4\) .
- For \(y^2 - 6y\) , add \(\left(\frac{-6}{2}\right)^2 = 9\) .
Add these same values to the right-hand side: \[(x^2 + 4x + 4) + (y^2 - 6y + 9) = -9 + 4 + 9\]
Simplify and rewrite the equation: \[(x + 2)^2 + (y - 3)^2 = 4\]
Comparing this to the standard form of a circle, we see that the center is \((-2, 3)\) , and the radius is \(R = 2\) (since \(R^2 = 4\) ).