To expand algebraic expressions, we need to use the distributive property. The reverse of expansion, called factorization or factoring , consists of using the distributive property in reverse and writing the expression as product of simpler ones. For example, we can write

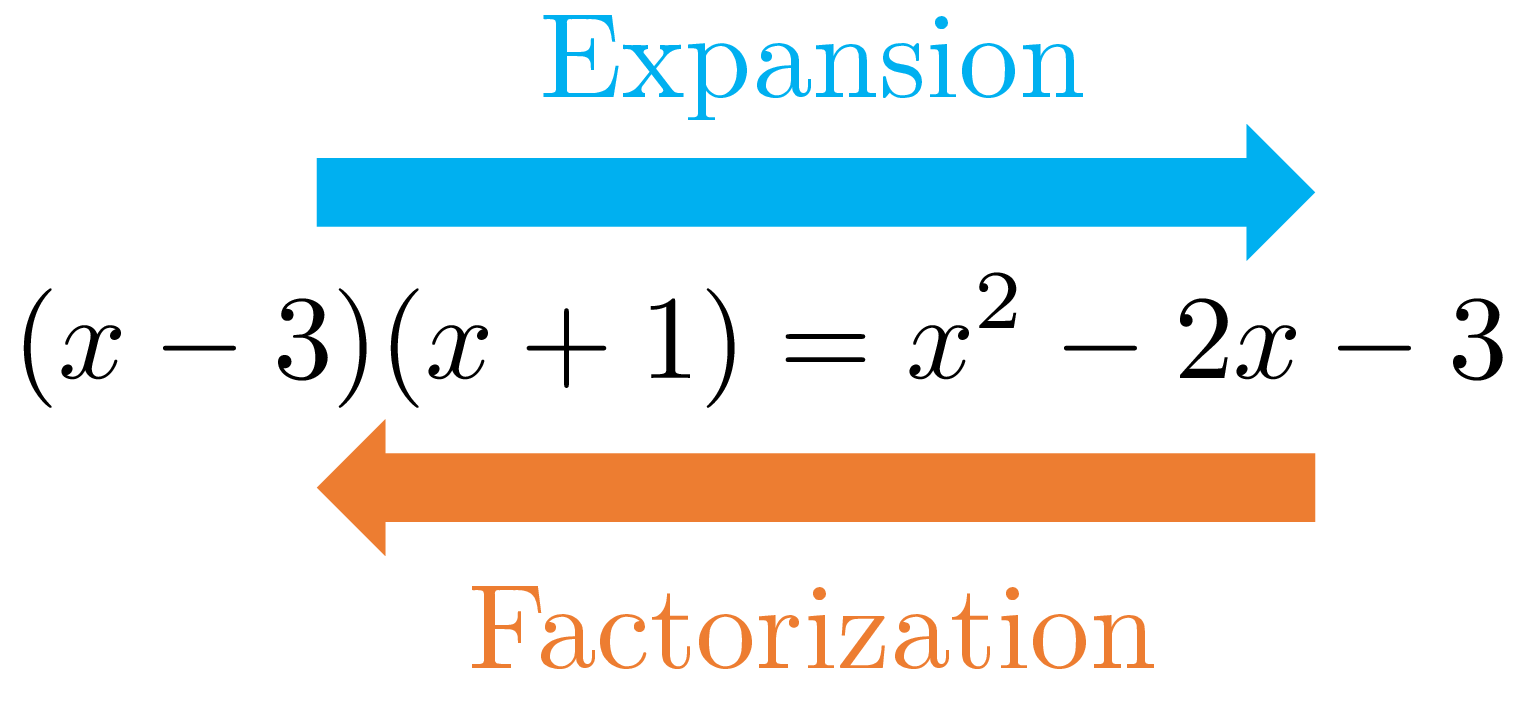
image

We say that \(x-3\) and \(x+1\) are factors of \(x^{2}-2x-3\) .

 

Why Is Factorization Important?

If we can put an equation in a factored form \(P\cdot Q=0\) , where \(P\) and \(Q\) are expressions in terms of the unknown variable, solving the problem reduces to solving two independent and often simpler equations \(P=0\) and \(Q=0\) . (Recall from Section: Sets of Numbers that if \(ab=0\) then \(a=0\) or \(b=0\) ). For example, because \(x^{2}-2x-3=(x-3)(x+1)\) , instead of solving \[x^{2}-2x-3=0,\] we can solve \[x-3=0\quad,\quad x+1=0\] which shows at once \[x=3\quad\text{or}\quad x=-1.\] Similarly because \[x^{3}-8x^{2}+17x-10=(x-1)(x-2)(x-5)\] we immediately conclude \[x^{3}-8x^{2}+17x-10=0\Leftrightarrow x=1\quad\text{or}\quad x=2\quad\text{or}\quad x=5.\] Also evaluating \(x^{3}-8x^{2}+17x-10\) reduces to only three subtractions and two multiplications.

Factorization is not always possible, and even when it is possible, it does not necessarily yield simpler factors. For example, \(x^{5}-32\) can be factored into \(x-2\) and \(x^{4}+2x^{3}+4x^{2}+8x+16\) , but clearly we would rather solve \(x^{5}-32=x^{5}-2^{5}=0\) than solve the following two equations \[x-2=0,\quad x^{4}+2x^{3}+4x^{2}+8x+16=0.\] 

Another application of factorization can be simplification of rational expressions. For example, \((x^{2}-1)/(x^{2}-2x-3)\) can be simplified as \[\frac{x^{2}-1}{x^{3}-2x-3}=\frac{(x-1)\cancel{(x+1)}}{(x-3)\cancel{(x+1)}}=\frac{x-1}{x-3}\qquad(x\neq-1)\] 

Now let’s review some techniques of factorization.

Common Factors

When there is a factor common to every term of an expression, we can simply factor it out by applying the distributive property in reverse.

Example 1.21 . Factor each expression 
(a) \(12x^{3}-15x^{2}\) 
(b) \(4x^{5}-8x^{4}-16x^{3}-20x^{2}\) 
(c) \((2x-5)(3x-7)+4(3x-7)\) 

 

Solution

(a) The greatest common factor of the terms \(12x^{3}\) and \(-15x^{2}\) is \(3x^{2}\) , so we have \[12x^{3}-15x^{2}=3x^{2}(4x-5)\] (b) The greatest common factor of all terms is \(4x^{2}\) , so we have \[4x^{5}-8x^{4}-16x^{3}-20x^{2}=4x^{2}\left(x^{3}-2x^{2}-4x-5\right).\] (c) The greatest common factor of \((2x-5)(3x-7)\) and \(4(3x-7)\) is \((3x-7)\) . Thus \[\begin{align} (2x-5)(3x-7)+4(3x-7) & =(3x-7)\left[(2x-5)+4\right]\\ & =(3x-7)(2x-1)\tag{after simplification} \end{align}\] 

 

In calculus sometimes we need to factor expressions with fractional or negative exponents. In this case, we factor out the common factor with the smallest exponent. 

Example 1.22 . Factor each expression 
(a) \(x^{3/2}+4x^{1/2}-7x^{-1/2}\) 
(b) \((x-4)^{-3/5}+5(x-4)^{2/5}\) 

 

Solution

(a) The common factor is \(x\) and its smallest exponent is \(-1/2\) . Thus \[x^{3/2}+4x^{1/2}-7x^{-1/2}=x^{-1/2}(x^{2}+4x-7)\] Note that \(x^{-1/2}x^{2}=x^{(2-1/2)}=x^{3/2}\) and \(x^{-1/2}x=x^{(1-1/2)}=x^{1/2}\) . 
(b) The common factor is \(x-4\) and its smallest exponent is \(-3/5\) . Thus \[\begin{align} (x-4)^{-3/5}+5(x-4)^{2/5} & =(x-4)^{-3/5}\left[1+(x-4)^{1}\right]\\ & =(x-4)^{-3/2}(x-3). \end{align}\] Note \((x-4)^{-3/5}\cdot(x-4)=(x-4)^{(1-3/5)}=(x-4)^{2/5}\) .

 

Special Factorization Formulas

If there is no common factor, to factor algebraic expressions we can sometimes use the following formulas that we reviewed in Section: Special Product and reverse the process.

  1. \(A^{2}-B^{2}=(A+B)(A-B)\) (Difference of Squares)
  2. \(A^{2}\pm2AB+B^{2}=(A\pm B)^{2}\) (Perfect Square)
  3. \(A^{3}-B^{3}=(A-B)(A^{2}+AB+B^{2})\) (Difference of Cubes)
  4. \(A^{3}+B^{3}=(A+B)(A^{2}-AB+B^{2})\) (Sum of Cubes)

How to memorize the Sum/Difference of Cubes formulas? Remember a cube of SOAP

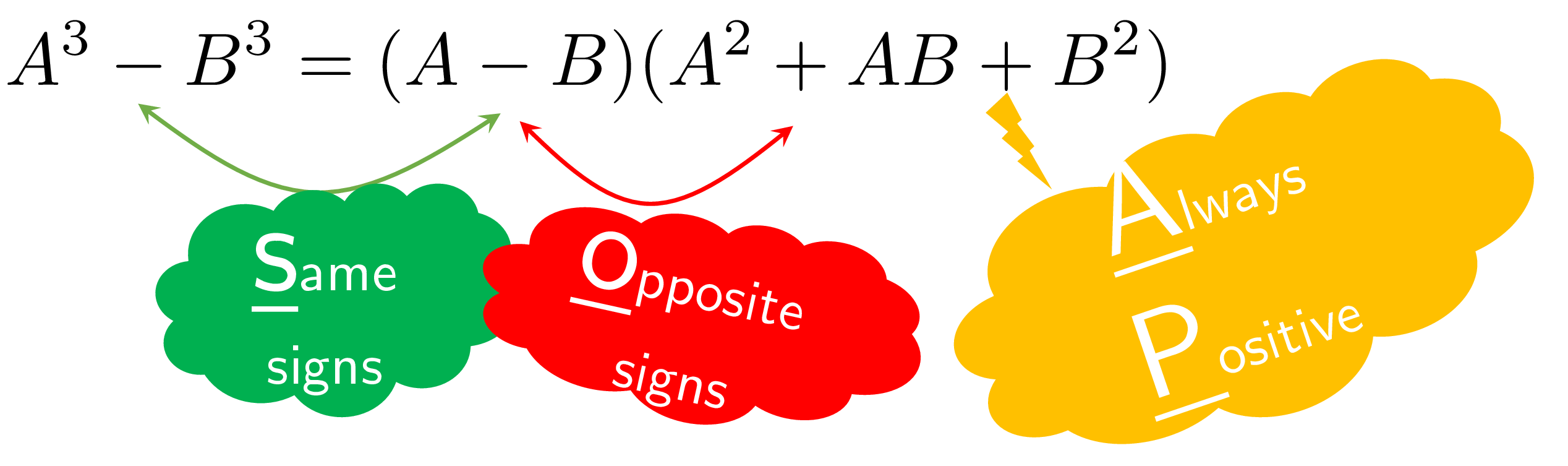
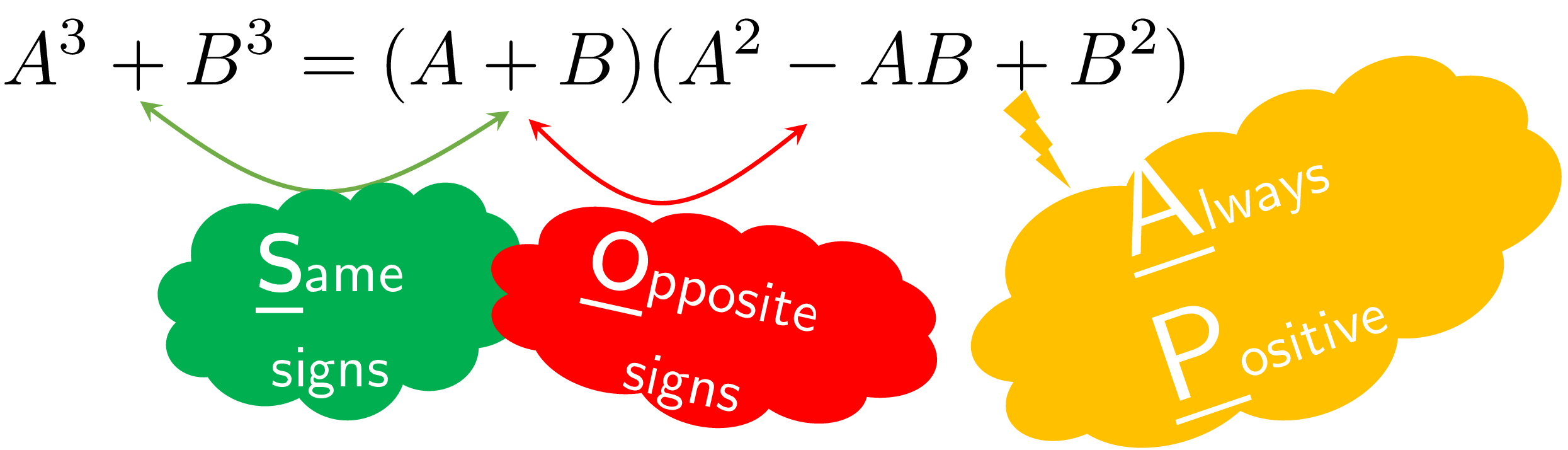
image

image

Example 1.23 . Factor each expression 
(a) \(9x^{2}-49\) 
(b) \(x^{4}-16\) 
(c) \(x^{2}+10x+25\) 
(d) \(x^{3}-27\) 
(e) \(8x^{3}+64\) 

 

Solution

(a) Rewriting as difference of squares \[9x^{2}-49=(3x)^{2}-7^{2}\] Let \(A=3x\) and \(B=7\) in \(A^{2}-B^{2}=(A-B)(A+B)\) . Then \[\begin{align} (3x)^{2}-7^{2} & =A^{2}-B^{2}\\ & =(A-B)(A+B)\\ & =(3x-7)(3x+7). \end{align}\] (b) Let \(A=x^{2}\) and \(B=4\) , then \[\begin{align} x^{4}-16 & =A^{2}-B^{2}\\ & =(A-B)(A+B)\\ & =(x^{2}-4)(x^{2}+4) \end{align}\] We note that we can rewrite \(x^{2}-4\) as \(x^{2}-2^{4}\) , so we can use the Difference of Squares formula and factor it as \[x^{2}-2^{2}=(x-2)(x+2)\] Thus \[\begin{align} x^{4}-16 & =(x^{2}-4)(x^{2}+4)\\ & =(x-2)(x+2)(x^{2}+4). \end{align}\] (c) Let \(A=x\) and \(B=5\) . Because the middle term \(10x=2AB\) , the polynomial is a perfect square. By the Perfect Square formula we have \[x^{2}+10x+25=(x+5)^{2}.\] (d) Let \(A=x\) and \(B=3\) , then \[\begin{align} x^{3}-27 & =A^{3}-B^{3}\\ & =(A-B)(A^{2}+AB+B^{2})\\ & =(x-3)(x^{2}+3x+9). \end{align}\] (e) Here the terms \(8x^{3}\) and 64 have the common factor 8, so first of all we factor it out. \[8x^{3}+64=8(x^{3}+8).\] Then we can use the Sum of Cubes formula with \(A=x\) and \(B=2\) : \[\begin{align} x^{3}+8 & =A^{3}+B^{3}\\ & =(A+B)(A^{2}-AB+B^{2})\\ & =(x+2)(x^{2}-2x+4). \end{align}\] Therefore \[\begin{align} 8x^{3}+64 & =8(x^{3}+8)\\ & =8(x+2)(x^{2}-2x+4). \end{align}\] 

 

Example 1.24 . Factor \(9x^2-12xy+4y^2\) .

 

Solution

Notice that \(9x^2=(3x)^2\) and \(4y^2=(2y)^2\) . Since \[12xy=2 (3x)(2y)\] we have a perfect square. Given that the sign of the middle term is negative, we factor as \[9x^2-12xy+4y^2=(3x-2y)^2=(2y-3x)^2.\] 

 

Example 1.25 . Factor \(a^2+b^2+c^2+2 a b+2 a c+2 b c\) .

 

Solution

We can reduce this to the form of a trinomial square by grouping the terms thus: \[\begin{align} a^2+2 a b+b^2+2 a c+2 b c+c^2 & =(a+b)^2+2(a+b) c+c^2 \\ & =(a+b+c)^2 \end{align}\] 

 

Example 1.26 . Factor \(x^2-y^2-z^2+2 y z\) .

 

Solution

\[\begin{align} x^2-y^2-z^2+2 y z & =x^2-\left(y^2-2 y z+z^2\right) \\ & =x^2-(y-z)^2 \\ &\qquad\qquad\qquad(\text{Now use }A^2-B^2=(A-B)(A+B)\ ) \\ & =(x+y-x)(x-y+z) \end{align}\] 

 

Example 1.27 . Factor \(x^4+x^2 y^2+y^4\) .

 

Solution

\[\begin{align} x^4+x^2 y^2+y^4 & =x^4+2 x^2 y^2+y^4-x^2 y^2 \\ & =\left(x^2+y^2\right)^2-x^2 y^2 \\ & =\left(x^2+y^2+x y\right)\left(x^2+y^2-x y\right) \end{align}\] 

 

More Special Factorization Formulas 

In general we can factor the sum or difference of two \(n\) th power ( \(n\) an integer) as follows

  • Difference, even exponent: 
    \(A^{2n}-B^{2n}=(A^{n}-B^{n})(A^{n}+B^{n})\)
  • Difference, even or odd exponent: 
    \(A^{n}-B^{n}=(A-B)(A^{n-1}+A^{n-2}B+A^{n-3}B^{2}+\cdots+AB^{n-2}+B^{n-1})\) 

If we replace \(B\) with \(-B\) in the above formula and \(n\) is odd then we will get the following formula (Note that if \(n\) is even, we won’t get a new formula).

  • Sum, odd exponent: 
    \(A^{n}+B^{n}=(A+B)(A^{n-1}-A^{n-2}B+A^{n-3}B^{2}-\cdots-AB^{n-2}+B^{n-1})\)
  • Sum, even exponent: \(A^{n}+B^{n}\) cannot, in general, be factored.

Factorization of Polynomials of the Form \(x^{2}+bx+c\) by Inspection

It is sometimes possible to factor \(x^2 + bx + c\) by inspection when \(b\) and \(c\) are integers.

Since \[(x+p)(x+q) = x^{2} + (p+q)x + pq,\] we can factor polynomials of the form \(x^{2} + bx + c\) if we can find numbers \(p\) and \(q\) such that: \[p + q = b \quad \text{and} \quad pq = c.\] 

While such numbers are rarely rational, when they are, they must be integers (see Rational Root Theorem ). In other words, we do not consider fractions like \(1/2\) or \(3/7\) during inspection.

In this section, we choose \(p\) and \(q\) by trial and error. Later , we will learn a systematic method to find these values.

Example 1.28 . Factor \(x^2+18 x+42\) .

 

Solution

We seek two integers, \(p\) and \(q\) , whose product is 42 and sum 18. As both \(p q\) and \(p+q\) are positive, both \(p\) and \(q\) must be positive. Hence among the positive integers whose product is 42—namely, 42 and 1, 21 and 2 , 14 and 3, 7 and \(6\) —we seek a pair whose sum is 13 , and find 7 and 6.

 

Hence \[x^2+18 x+42=(x+7)(x+6).\] 

Example 1.29 . Factor \(x^2-13 x+22\) .

 

Solution

Here both \(p\) and \(q\) must be negative; for their product is positive and their sum negative. Hence, testing as before the pairs of negative integers whose product is 22 , we find \(-11\) and \(-2\) ; for \(-11-2=-13\) .

 

Hence \[x^2-18 x+22=(x-11)(x-2).\] 

Example 1.30 . Factor \(x^2-9 x-22\) .

 

Solution

Here, since \(p q\) is negative, \(p\) and \(q\) must have opposite signs; and since \(p+q\) is negative, the one which is numerically greater must be negative. Hence we set \(-22=-22 \times 1=-11 \times 2\) , and, testing as before, find \(p=-11\) and \(q=2\) ; for \(-11+2=-9\) .

 

Hence \[x^2-9 x-22=(x-11)(x+2).\] 

Example 1.31 . Factor each expression 
(a) \(x^{2}+3x+2\) 
(b) \(x^{2}-2x-15\) 

 

Solution

(a) We need to find \(p\) and \(q\) such that \(p+q=3\) and \(pq=2\) . By trial and error we find that they are 2 and 1. Thus the factorization is \[x^{2}+3x+2=(x+2)(x+1).\] (b) We need to choose \(p\) and \(q\) such that \(p+q=-2\) and \(pq=-15\) . By trial and error we find that they are \(-5\) and \(3\) . Thus \[x^{2}-2x-15=(x-5)(x+3).\] 

 

Factorization of Polynomials of the Form \(ax^{2}+bx+c\) by Inspection

It is sometimes possible to factor \(ax^2+bx+c\) by trial and error, when \(a, b\) , and \(c\) are integers.

By multiplying and dividing by \(a\) , we may reduce \(a x^2+b x+c\) to the form \(\left[(a x)^2+b(a x)+a c\right] / a\) , and then factor the bracketed expression with respect to \(a x\) by the method just explained, namely, by finding two integers whose product is \(a c\) , and sum \(b\) .

Here’s the edited version:

Example 1.32 . Factor \(6x^2 + 7x - 5\) .

 

Solution

Let’s rewrite the expression: \[6x^2 + 7x - 5 = \frac{(6x)^2 + 7(6x) - 5 \times 6}{6}\] Let \(u = 6x\) : \[(6x)^2 + 7(6x) - 30 = u^2 + 7u - 30\] and then factor the result. We need to find two numbers, \(p\) and \(q\) , such that \(p + q = 7\) and \(pq = -30\) . Since \(pq\) is negative, one of the numbers must be positive and the other negative. Since \(p + q\) is positive, the number with the greater absolute value must be positive.

 

We can list the factors of \(-30\) \[-30 = 30 \times (-1) = 10 \times (-3) = 6 \times (-5)\] The pair \(10\) and \(-3\) satisfy our conditions \(10 + (-3) = 7\) . Thus we find \(p = 10\) and \(q = -3\) and \[u^2 + 7u - 30 = (u + 10)(u - 3).\] Now, substitute \(6x\) for \(u\) : \[(6x)^2 + 7(6x) - 30 = (6x + 10)(6x - 3)\] Finally, we simplify: \[\begin{align} 6x^2 + 7x - 5 &= \frac{(6x)^2 + 7(6x) - 30}{6} = \frac{(6x + 10)(6x - 3)}{6} \\ &= (3x + 5)(2x - 1) \end{align}\] 

Example 1.33 . Factor \(2 x+7 x+3\) .

 

Solution

We have \[\begin{align} 2 x^2+7 x+3 & =\frac{(2 x)^2+7(2 x)+6}{2} \\ & =\frac{(2 x+6)(2 x+1)}{2}=(x+8)(2 x+1) \end{align}\] 

 

Example 1.34 . Factor \(a b x^2+\left(a^2+b^2\right) x+a b\) .

 

Solution

We have \[\begin{align} a b x^2+\left(a^2+b^2\right) x+a b & =\frac{(a b x)^2+\left(a^2+b^2\right) \cdot a b x+a^2 b^2}{a b} \\ & =\frac{\left(a b x+a^2\right)\left(a b x+b^2\right)}{a b} \\ & =(b x+a)(a x+b) . \end{align}\] 

 

Example 1.35 . Factor \(16 x^2+72 x-63\) .

 

Solution

In this case it is not necessary to multiply and divide by 16, for we have \[\begin{align} 16 x^2+72 x-63 & =(4 x)^2+18(4 x)-63 \\ & =(4 x+21)(4 x-3) \end{align}\] 

 

Factorization of \(ax^2+bx+c\) by Completing the Square 

While the preceding methods apply in particular cases only, the following is perfectly general.

Since \[\left(x+\frac{p}{2}\right)^2=x^2+p x+\frac{p^2}{4}\] we can make \(x^2+p x\) a perfect square by adding \(\frac{p^2}{4}\) , that is, the square of half the coefficient of \(x\) .

This process is called completing the square of \(x^2+p x\) .

  1. We will not affect the value of \(x^2+p x+q\) , if we both add and subtract \(p^2 / 4\) . But by this means we can transform the expression into the difference between two squares and then factor it by \(A^2-B^2=(A-B)(A+B)\) . Thus, \[\begin{align} x^2+p x+q & =x^2+p x{\color{red}{+\frac{p^2}{4}-\frac{p^2}{4}}}+q \\ & =\left(x+\frac{p}{2}\right)^2-\frac{p^2-4 q}{4} \\ &=\left(x+\frac{p}{2}+\frac{\sqrt{p^2-4 q}}{2}\right)\left(x+\frac{p}{2}-\frac{\sqrt{p^2-4 q}}{2}\right)\\ & =\left(x+\frac{p+\sqrt{p^2-4 q}}{2}\right)\left(x+\frac{p-\sqrt{p^2-4 q}}{2}\right) &&(i) \end{align}\]
  2. Since \[a x^2+b x+c=a\left(x^2+\frac{b}{a} x+\frac{c}{a}\right),\] we may obtain the factors of this expression by substituting \(b / a\) for \(p\) and \(c / a\) for \(q\) in Equation (i). Simplifying the result, we have \[a x^2+b x+c=a\left(x+\frac{b+\sqrt{b^2-4 a c}}{2 a}\right)\left(x+\frac{b-\sqrt{b^2-4 a c}}{2 a}\right) .\] 

Example 1.36 . Factor \(x^2-6 x+2\) .

 

Solution

We have \[\begin{align} x^2-6 x+2 & =x^2-6 x+3^2-3^2+2 \\ & =(x-3)^2-7 \\ & =(x-3+\sqrt{7})(x-3-\sqrt{7}) \end{align}\] 

 

Example 1.37 . Factor \(3 x^2-5 x+1\) .

 

Solution

We have \[\begin{align} 3 x^2-5 x+1 & =3\left[x^2-\frac{5}{3} x+\frac{1}{3}\right] \\ & =3\left[x^2-\frac{5}{3} x+\left(\frac{5}{6}\right)^2-\left(\frac{5}{6}\right)^2+\frac{1}{3}\right] \\ & =3\left[\left(x-\frac{5}{6}\right)^2-\frac{13}{36}\right] \\ & =3\left(x-\frac{5}{6}+\frac{\sqrt{13}}{6}\right)\left(x-\frac{5}{6}-\frac{\sqrt{13}}{6}\right) \end{align}\] 

 

Example 1.38 . Factor \(x^2+8 x+20\) .

 

Solution

We have \[\begin{align} x^2+8 x+20 & =x^2+8 x+4^2-4^2+20 \\ & =(x+4)^2+4 \\ & =(x+4)^2-4 (\sqrt{-1})^2 \\ &=(x+4)^2-(2\sqrt{-1})^2\\ & =(x+4+2\sqrt{-1})(x+4-2\sqrt{-1}) \end{align}\] Here we first obtain a sum of squares, \((x+4)^2+4\) , and then transform this sum into a difference by replacing 4 by \(-4(\sqrt{-1})^2 =-4(-1)\) . Since the square root of a negative number is not defined within the real number system, this process introduces a new type of numbers, called complex numbers. For now, we’ll treat this factorization symbolically, and we will explore complex numbers in detail later.

 

Factorization by Grouping Terms

Sometimes there is no a common factor (other than \(\pm1\) ) to all terms of a polynomial. However, the polynomial can sometimes be factored if we suitably group the terms that have common factors. This strategy may work for polynomials with at least four terms.

For example, we can factor the polynomial \(x^{3}+3x^{2}+4x+12\) if we group the first two terms together and the last two terms together and then factor each group, namely \[\begin{align} x^{3}+3x^{2}+4x+12 & =(x^{3}+3x^{2})+(4x+12)\\ & =x^{2}(x+3)+4(x+3)\\ & =(x+3)(x^{2}+4)\tag{Factor out the common factor $(x+3)$} \end{align}\] 

Example 1.39 . Factor \(2x^{3}+x^{2}-18x-9\) .

 

Solution

\[\begin{align} 2x^{3}+x^{2}-18x-9 & =(2x^{3}+x^{2})-(18x+9) \tag{Group terms}\\ & =x^{2}(2x+1)-9(2x+1) \tag{ Factor out common factor of each group}\\ & =(2x+1)(x^{2}-9) \tag{Factor out $(2x+1)$}\\ & =(2x+1)(x-3)(x+3) \tag{Use Difference of Squares formula for $x^{2}-9=x^{2}-3^{2}$} \end{align}\]