Table of Contents
History
Before the 17th century, geometry and algebra were two very distinct branches of mathematics. In 1637 René Descartes, a French mathematician, scientist, and, philosopher, made a huge impact on the development of mathematical knowledge by unifying these two branches of mathematics. His approach is now called analytic geometry , the key feature of which is the use of a coordinate system. By means of coordinate systems, we can employ algebraic methods to study geometry and can geometrically represent algebraic equations. Analytic geometry is now widely used in mathematics, science, and engineering.
Points
In Section: Sets of Numbers , we showed how the real number system can be used to assign coordinates to points on a line.
Summary of assigning coordinates to points on a line
On a straight line, we choose a definite length as a unit distance and take a fixed point \(O\) from which to measure distances. Any point on this line represents a real number. Points on the right of \(O\) represent positive numbers and points on the left of \(O\) represent negative ones. The point \(O\) is called the origin and represents the number zero. To determine the position of a point on such a line, only one number is sufficient, namely the distance of the point, right or left, from the origin.
In the plane, to determine the position of a point \(P\) , we need two real numbers, namely a pair of numbers \((a,b)\) . We draw two perpendicular straight lines, label them as the \(x\) and \(y\) axes, designate their intersection as the origin, choose the same unit distance on both axes, and lay off distances from the origin along the axes. The distances to the right along the \(x\) -axis are taken as positive and those to the left as negative. In the same way, distances upward along the \(y\) -axis are taken as positive and those downward as negative.
In this case, the position of a point \(P\) in the plane can be clearly indicated by drawing two straight lines perpendicular to the axes, intersecting the \(x\) and \(y\) axes at \(M\) and \(N\) , respectively. Two signed distances \(a=\overline{OM}\) and \(b=\overline{ON}\) are called respectively the abscissa (or the \(x\) component) of \(P\) and the ordinate (or the \(y\) component) of \(P\) and together known as the rectangular coordinates or the Cartesian coordinates (in honor of René Descartes) of the point. In this case, we write \(P(a,b)\) (see the following figure ).
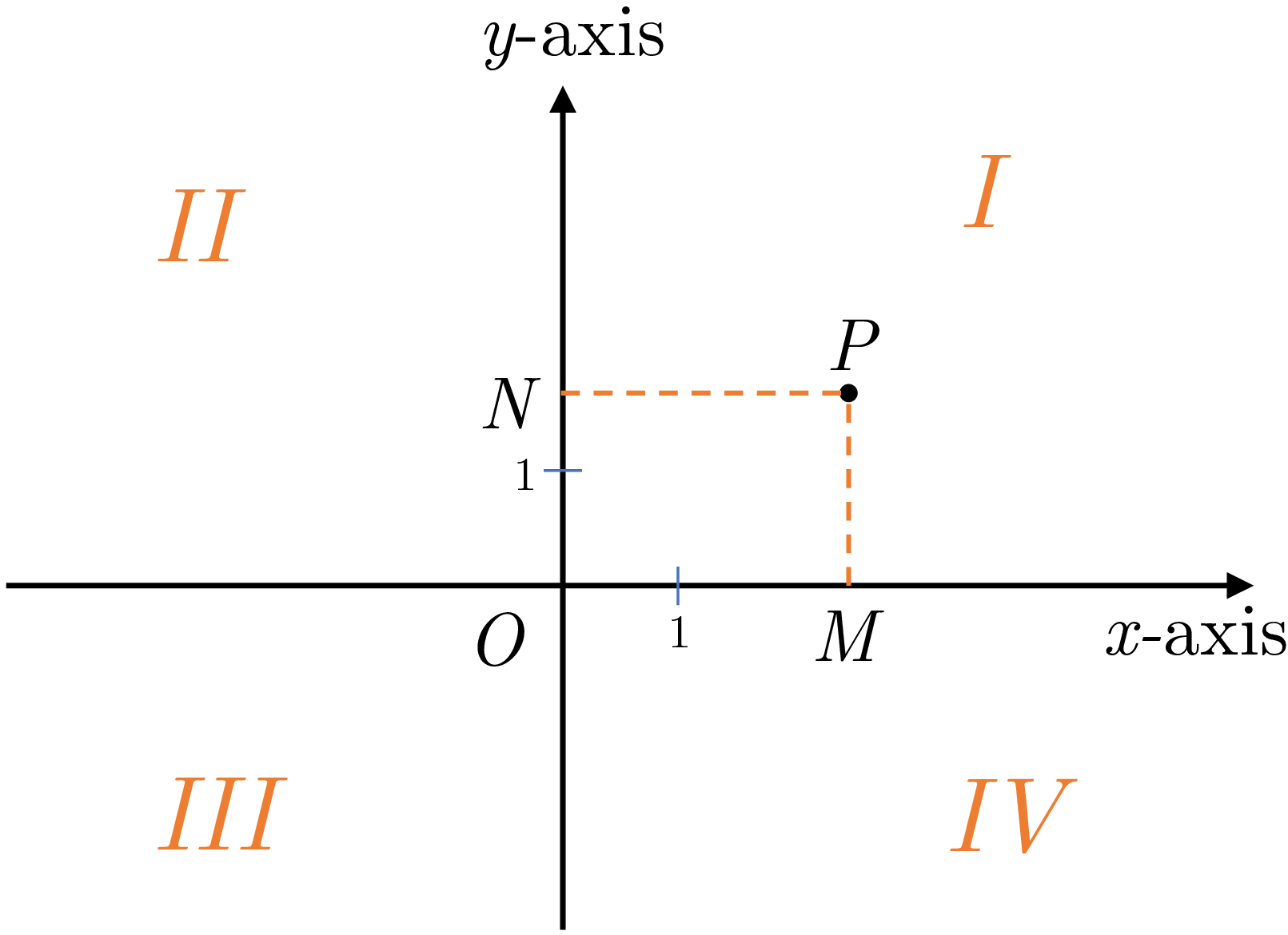
For example, to locate the point with coordinates \((4,-3)\) , we go out 4 units on the \(x\) -axis and \(-3\) units on the \(y\) -axis. But to locate the point with coordinates \((-3,4)\) , we go out \(-3\) units on the \(x\) -axis and 4 units on the \(y\) -axis. Obviously, a point with coordinates \((4,-3)\) is different from a point with coordinates \((-3,4)\) (See Figure 3.2 ). For this reason, the pair \((a,b)\) is often referred to as an ordered pair .
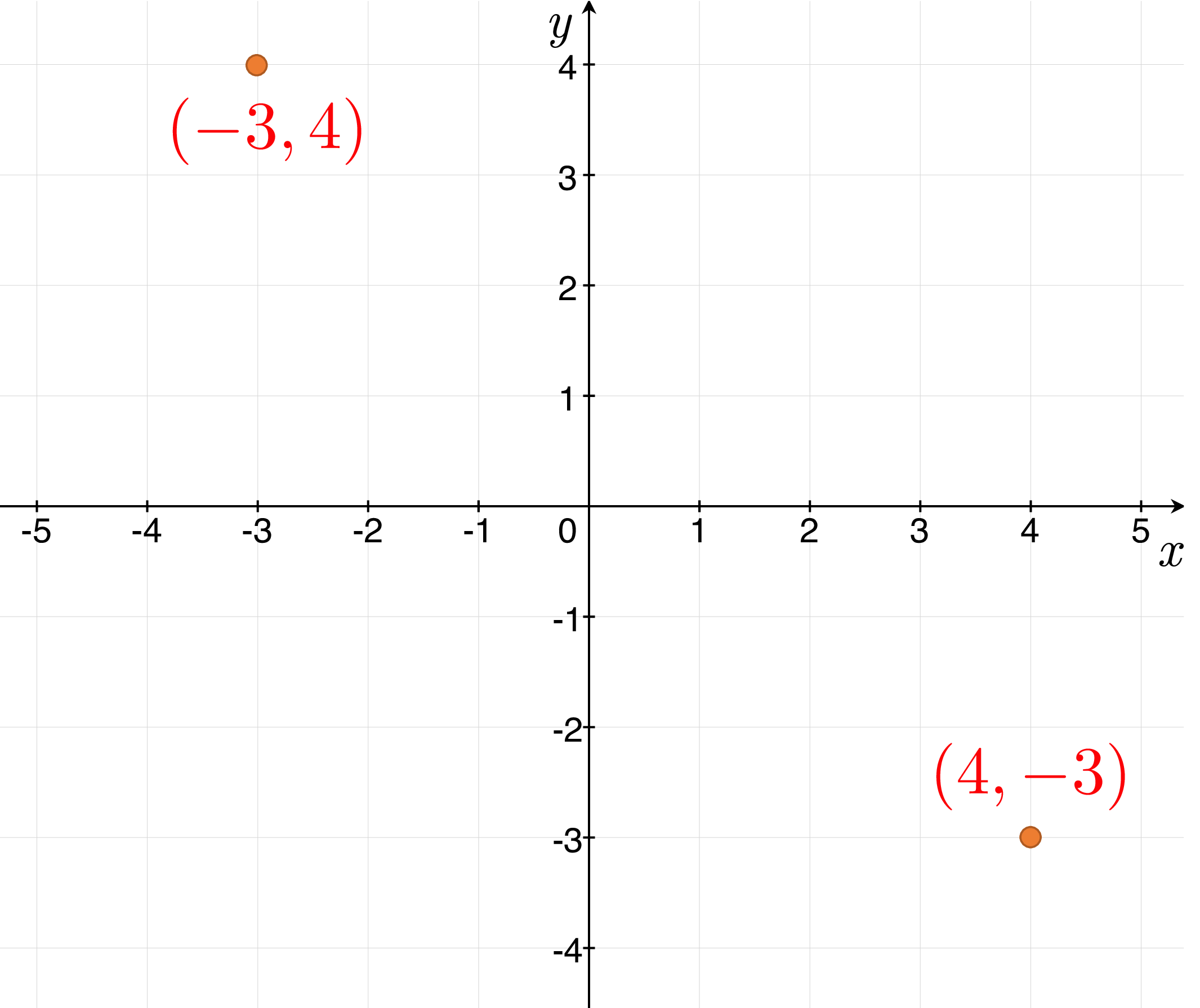
- The \(x\) and \(y\) axes divide all of the plane into four regions called quadrants. The quadrants are numbered I, II, III, and IV (called first, second, third, and fourth quadrants) as in first figure of this section.
- Instead of “the point with coordinates \((a,b)\) ”, we often simply say “the point \((a,b)\) .”
Don’t get confused about the symbol \((a,b)\) .
The symbol \((a,b)\) was previously used to denote an open interval, but in this section such a symbol represents a point. Whether the symbol \((a,b)\) represents an interval, a point, or some other mathematical object is often clear and can be understood from the context.
- The set of all ordered pairs is denoted by \(\mathbb{R\times R}\) or \(\mathbb{R}^{2}\) \[\mathbb{R}^{2}=\{(a,b)|\ a,b\in\mathbb{R}\}.\]
Example 1. Describe and sketch the regions given by the following sets
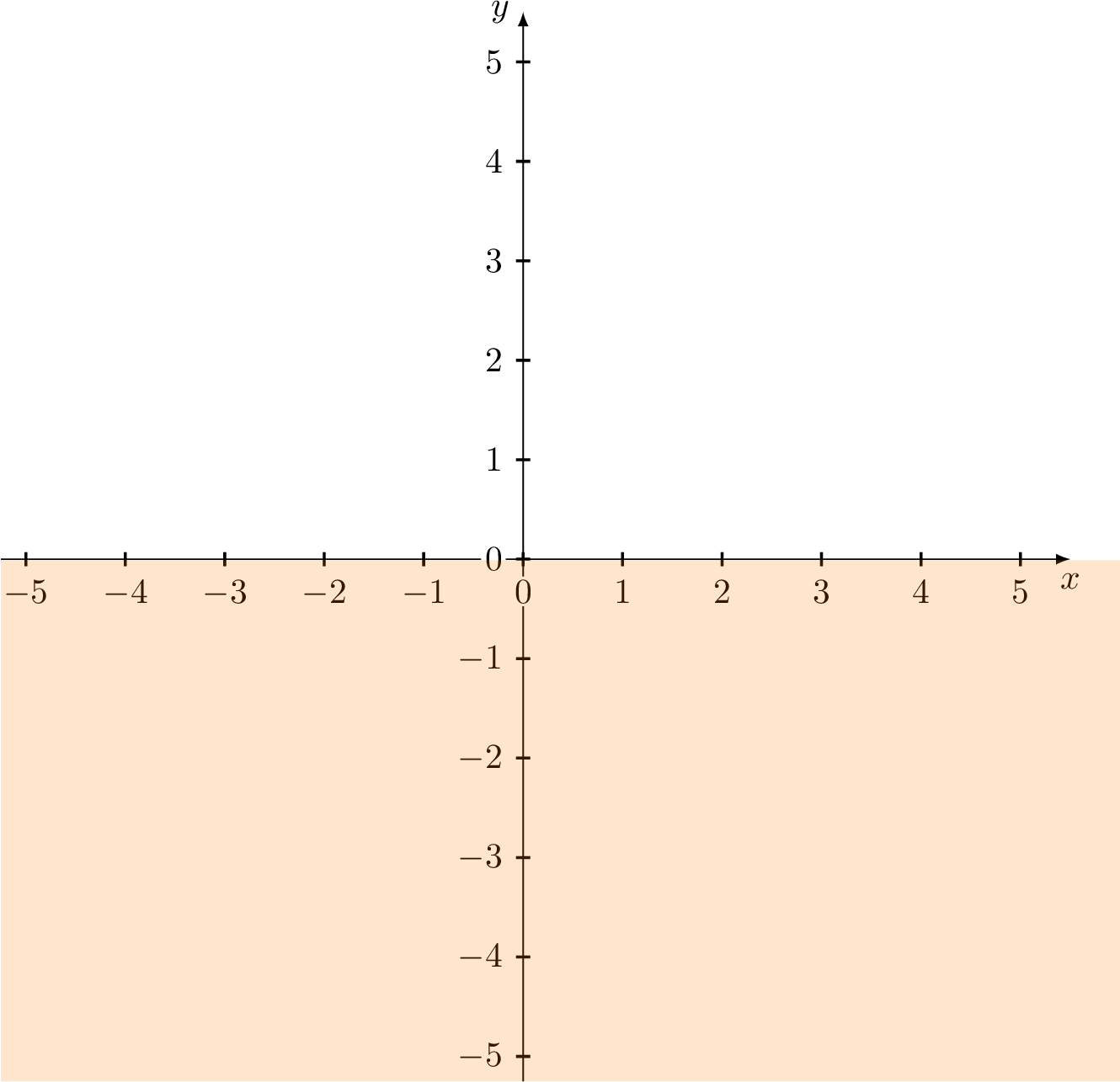
(a) \(\{(x,y)|\ y\le0\}\)
(b) \(\{(x,y)|\ x=2\}\)
(c) \(\{(x,y)|\ y=3\}\)
(d) \(\{(x,y)|\ x\geq2,y<3\}\)
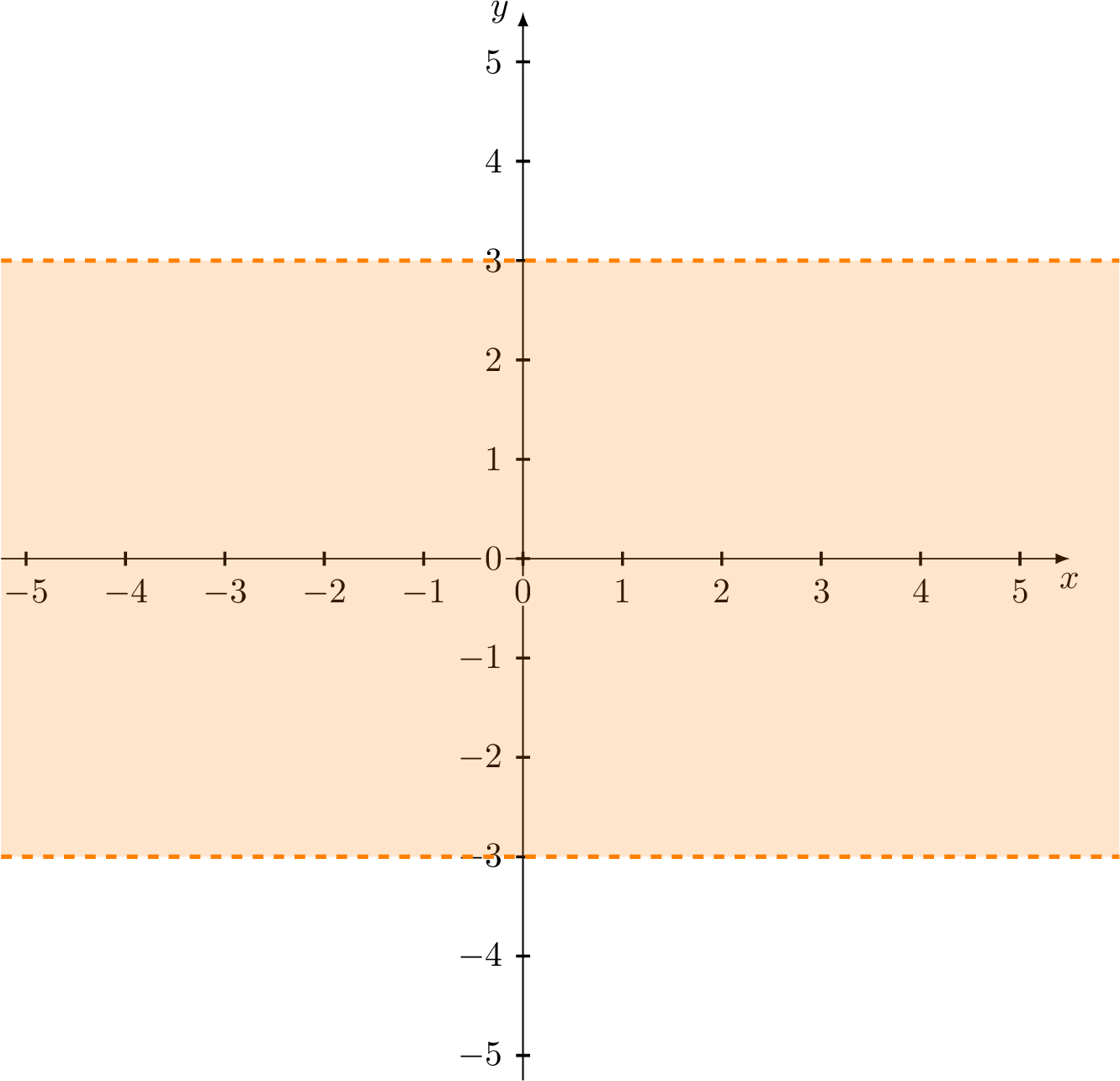
(e) \(\{(x,y)|\ |y|<3\}\)
Solution
(a) The set of all points whose \(y\) -coordinates are negative or zero consists of the \(x\) -axis and all points below the \(x\) -axis. This set is represented by the shaded region in the following figure.
(b) The set of all points with \(x\) -coordinate 2 is a vertical line 2 units to the right of the \(y\) -axis (see the following figure).
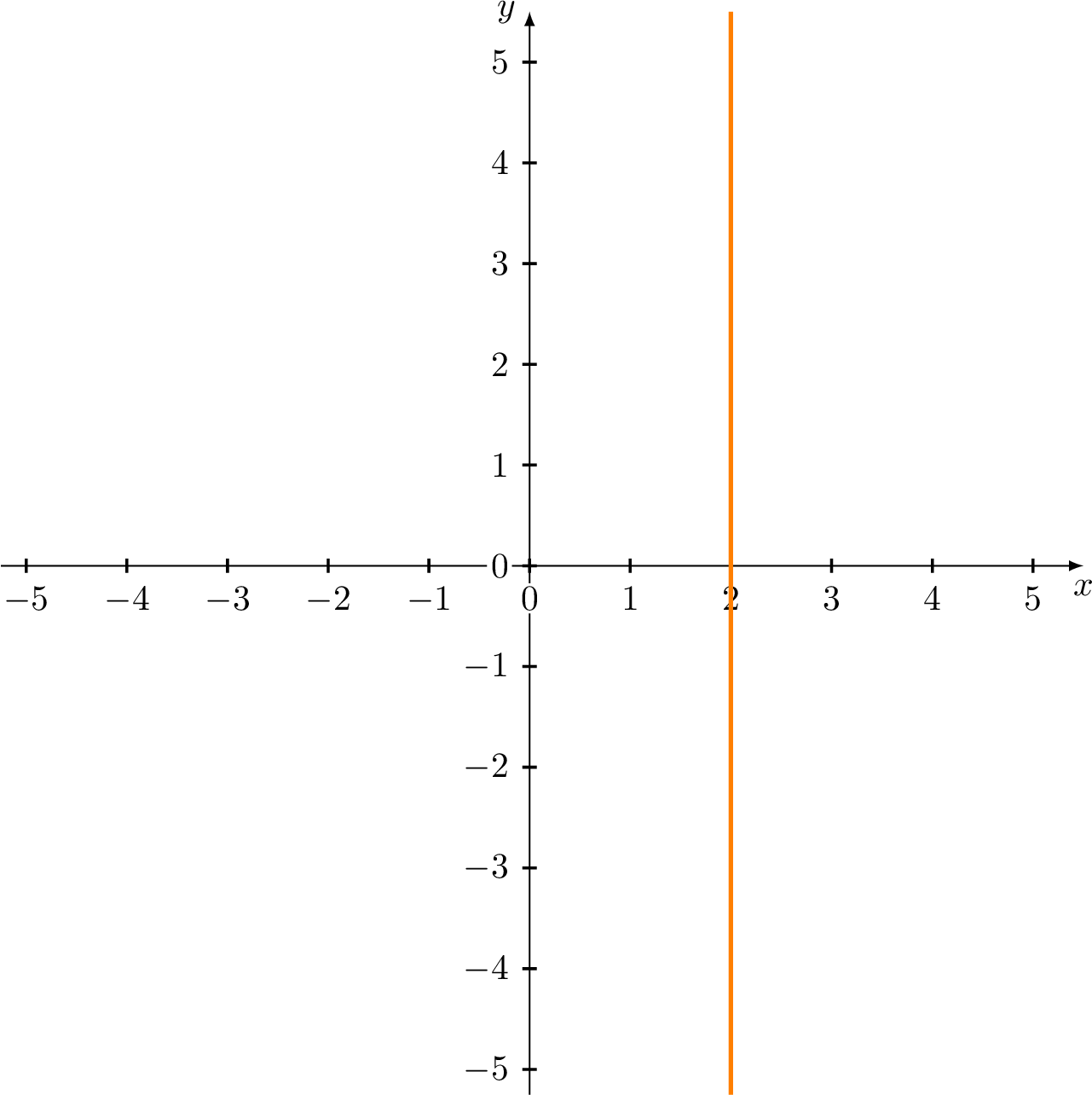
(c) The set of all points with \(y\) -coordinate 3 is a horizontal line 3 units above the \(x\) -axis (see the following figure)
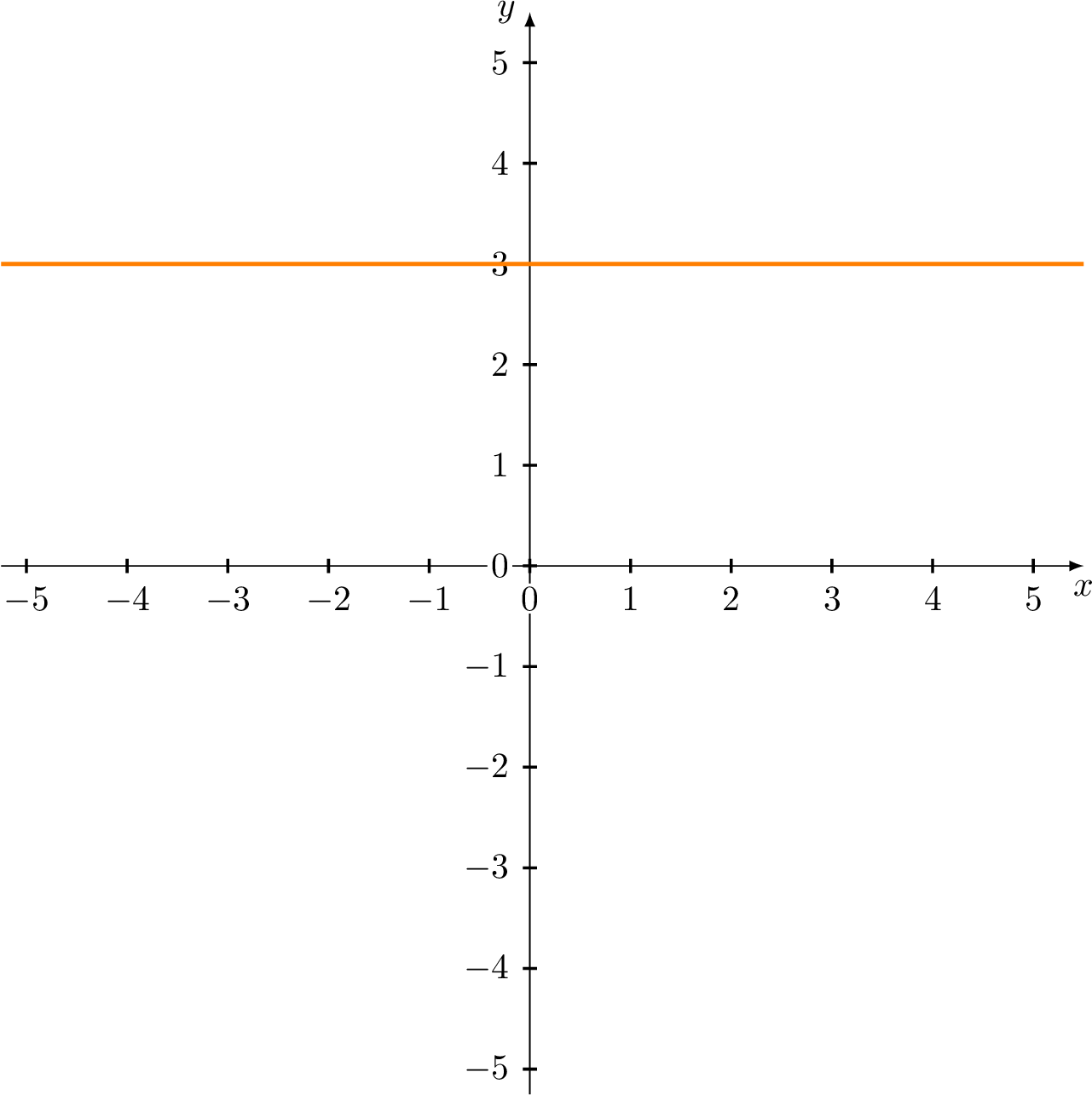
(d) The set of all points with \(x\) -coordinate greater or equal to 2 and \(y\) -coordinate less than 3 consists of points that lie on the vertical line \(x=2\) or to the right of it and below the line \(y=3\) , as indicated by the shaded region in the following figure. The dashed line indicates the points that do not lie in the set.

(e) Because \(|y|<3\) is equivalent to \(-3<y<3\) , this set consists of all points between the horizontal lines \(y=3\) (3 units above the \(x\) -axis) and \(y=-3\) (3 units below the \(x\) -axis).
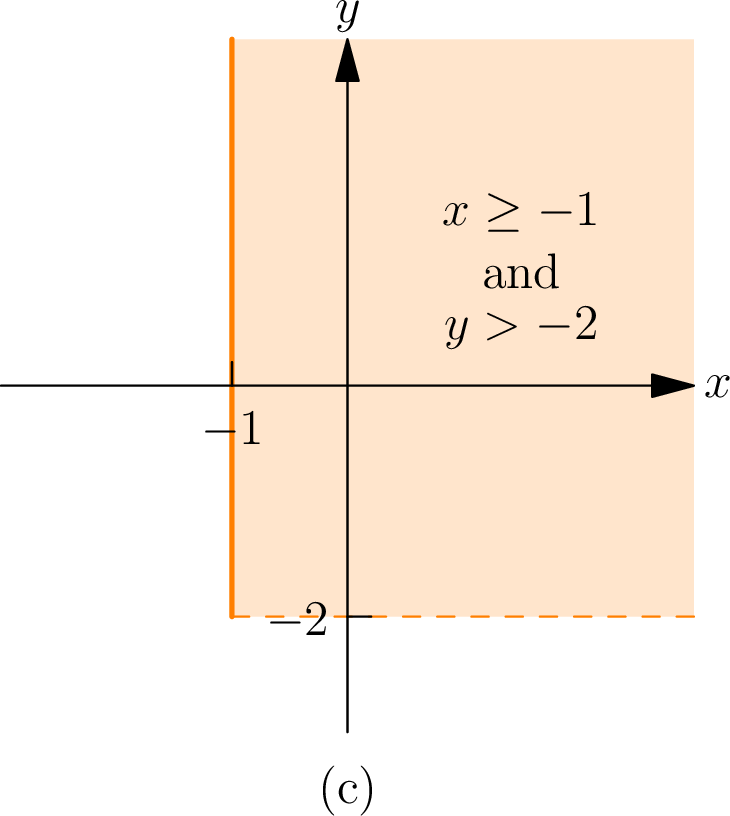
Example 2. Sketch the points in the \(xy\) -plane that satisfy both \(x \geq -1\) and \(y > -2\) .
Solution
The problem asks us to sketch the region described by: \[\{(x,y)\mid \ x\geq -1\text{ and } y>-2\}.\]
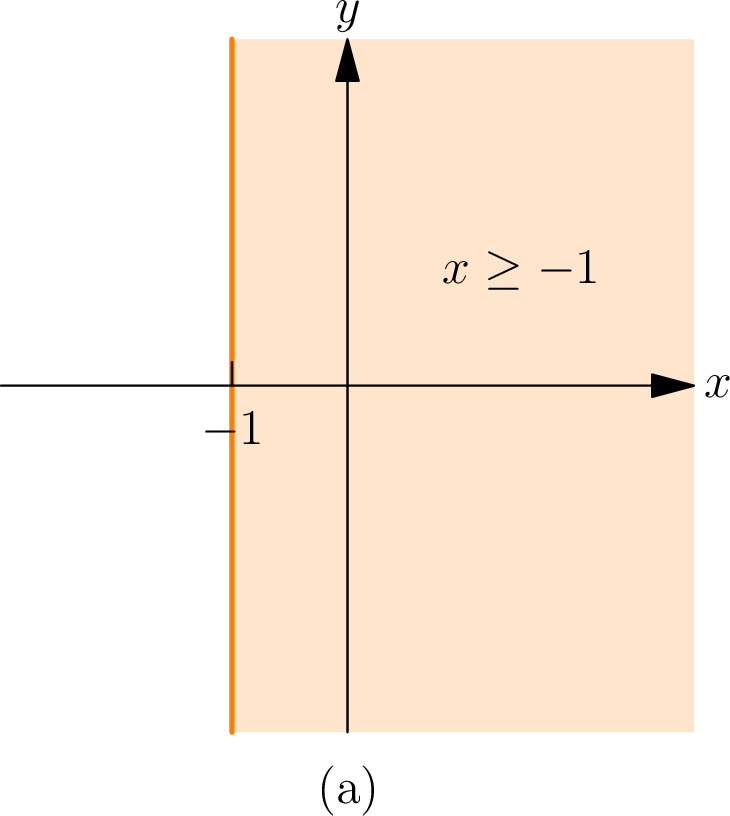
All points with \(x\) -coordinates greater than or equal to \(-1\) satisfy the inequality \(x \geq -1\) . This represents the half-plane to the right of (or on) the vertical line \(x=-1\) . The boundary line \(x=-1\) is included in the region.
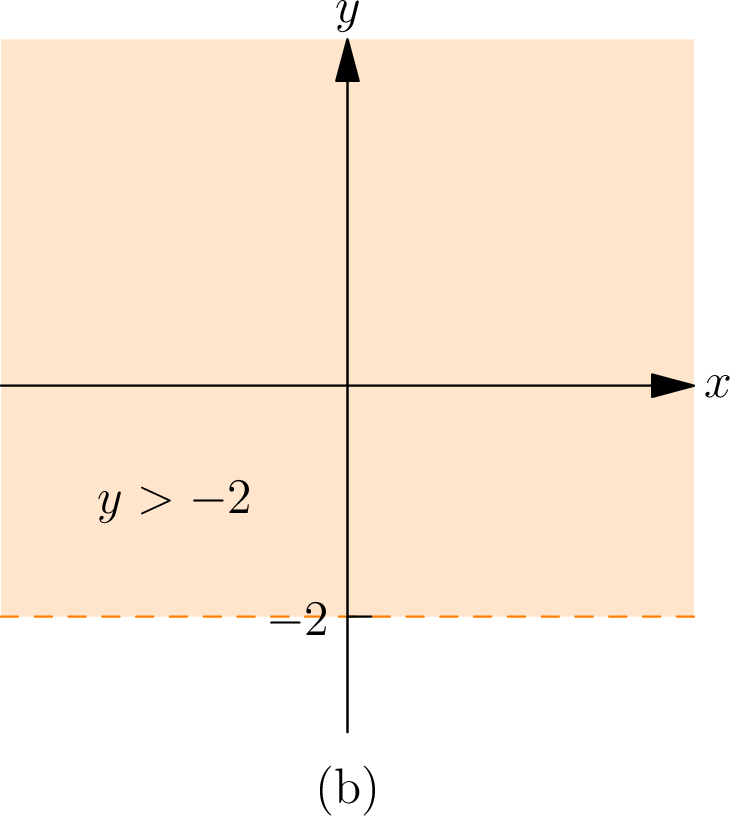
All points above the horizontal line \(y=-2\) satisfy the inequality \(y>-2\) . These points are shown below. Notice that the points on the horizontal line \(y=-2\) are not included.
The points satisfying both conditions are in the intersection of these two half-planes:
- All points to the right of or on the line \(x=-1\) , and
- Above the line \(y=-2\) .
The points satisfying both conditions are in the shaded region shown below.
Example 3. Sketch the points in the \(xy\) -plane that satisfy both inequalities \[1 \leq |x| < 3 \quad \text{and} \quad -2 \leq y \leq 1.\]
Solution
The first inequality, \(1 \leq |x| < 3\) , describes a restriction on the \(x\) -coordinates of the points. Recall that \(|x|\) represents the absolute value of \(x\) , which is the distance of the \(x\) -coordinate from the \(y\) -axis. This inequality means:
The distance of the \(x\) -coordinate from the \(y\) -axis must be at least \(1\) , so points closer to the \(y\) -axis (i.e., between \(x = -1\) and \(x = 1\) ) are excluded.
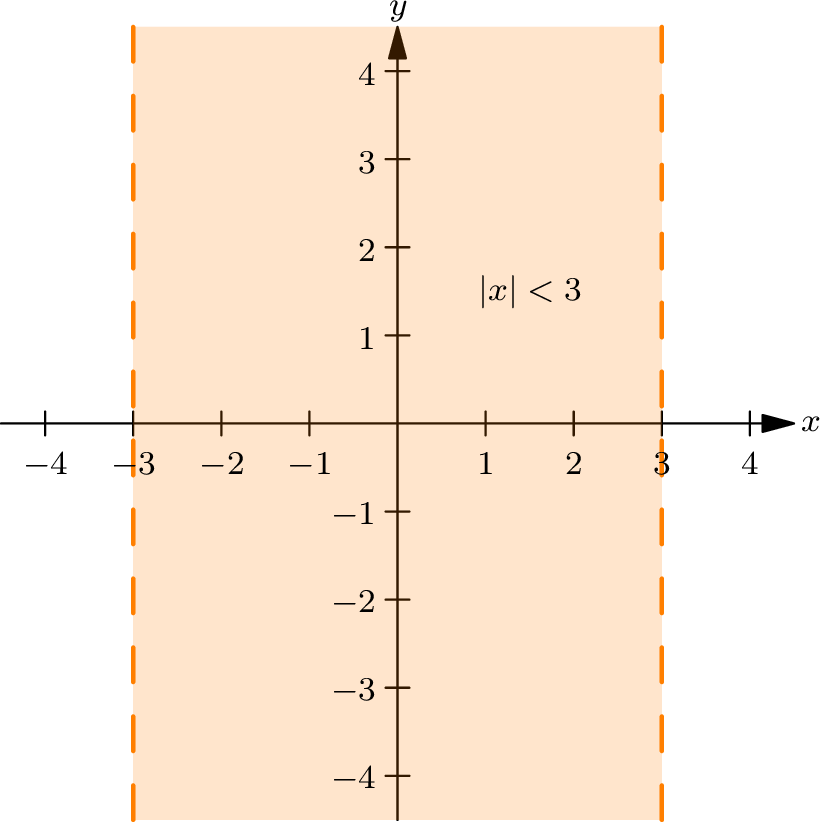
The distance must also be less than \(3\) , meaning points on or beyond the vertical lines \(x = 3\) and \(x = -3\) are excluded.
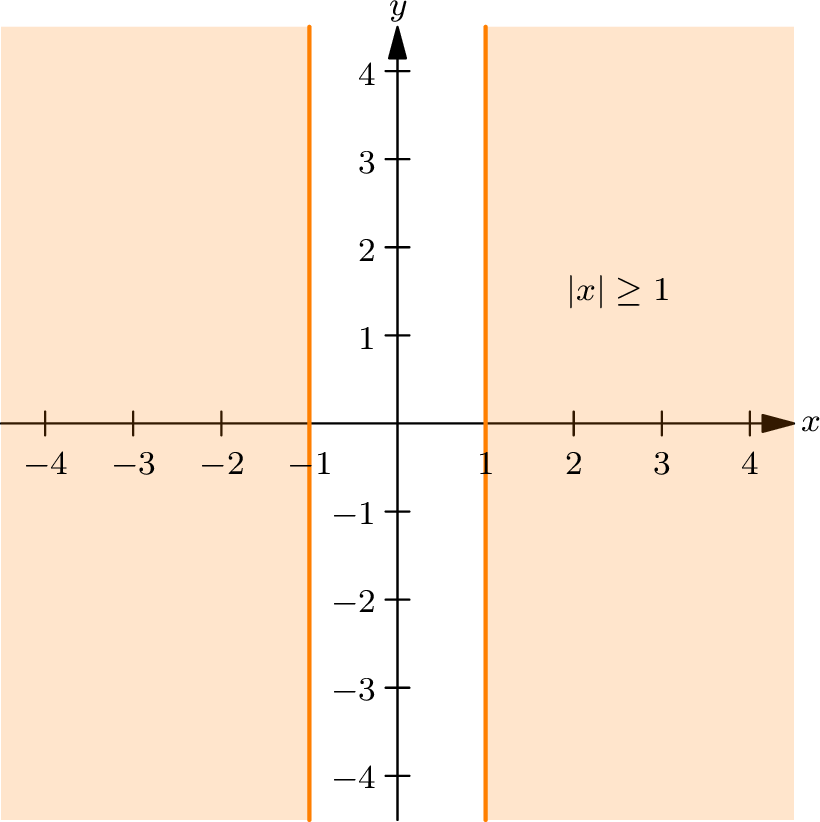
Thus, this inequality corresponds to the region in the \(xy\) -plane outside the vertical strip between \(x = -1\) and \(x = 1\) , but within the vertical lines \(x = -3\) and \(x = 3\) . The boundary lines \(x = -1\) and \(x = 1\) are not included, while the lines \(x = -3\) and \(x = 3\) are excluded as well. This region is shown shaded in the following figure.
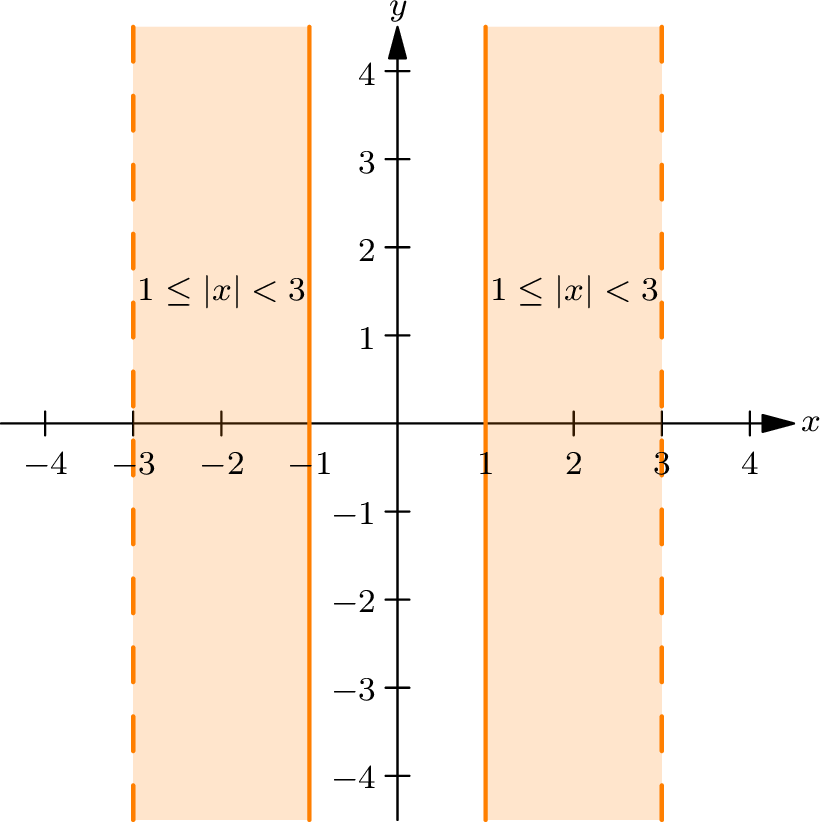
The second inequality, \(-2 \leq y \leq 1\) , describes a restriction on the \(y\) -coordinates of the points. It means:
- The \(y\) -coordinates must lie between \(-2\) and \(1\) , inclusive.
- Points on the boundary lines \(y = -2\) and \(y = 1\) are included in the region.
This inequality corresponds to the horizontal strip in the \(xy\) -plane between \(y = -2\) and \(y = 1\) , including the boundary lines. This region is shown below.
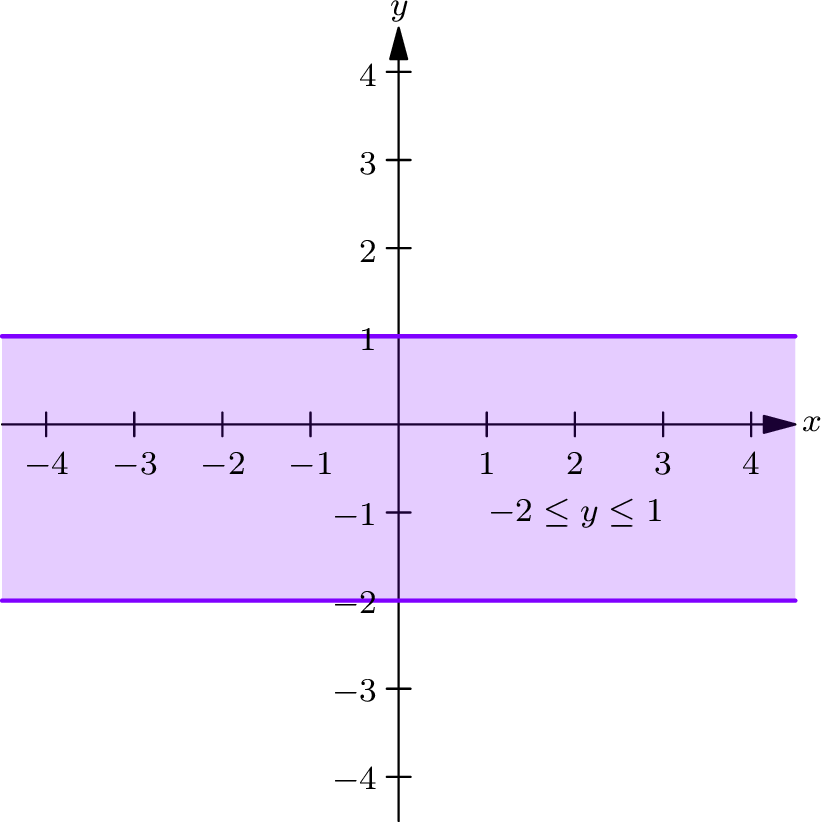
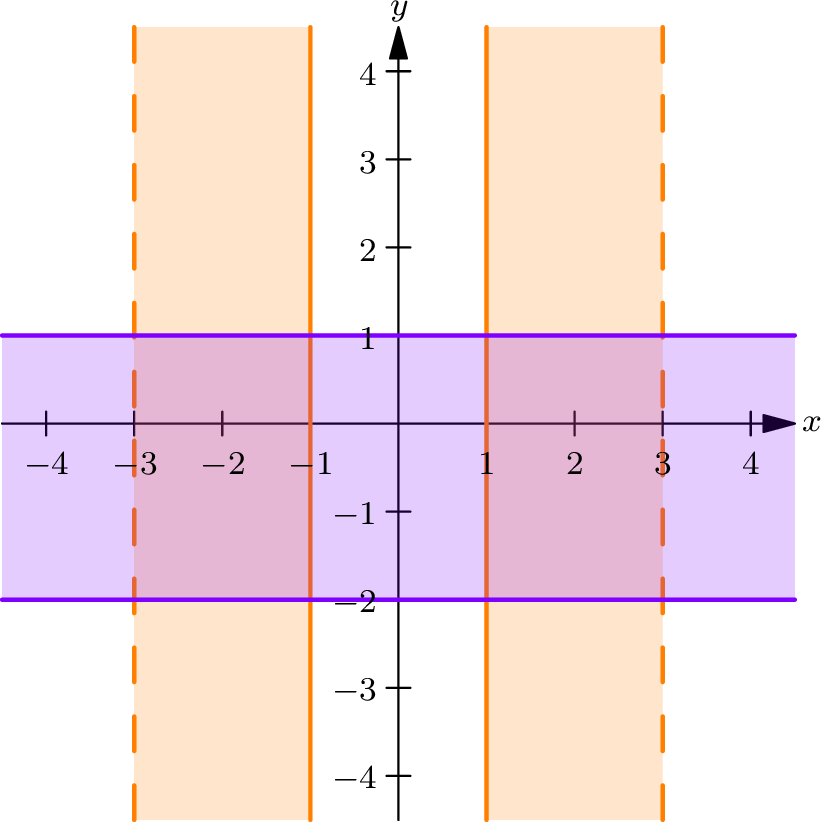
To find the points that satisfy both inequalities, we must identify the intersection of these two regions:
- The first region is the part of the \(xy\) -plane between the vertical lines \(x = -3\) and \(x = 3\) , excluding the strip between \(x = -1\) and \(x = 1\) .
- The second region is the part of the \(xy\) -plane between the horizontal lines \(y = -2\) and \(y = 1\) , including these boundaries.
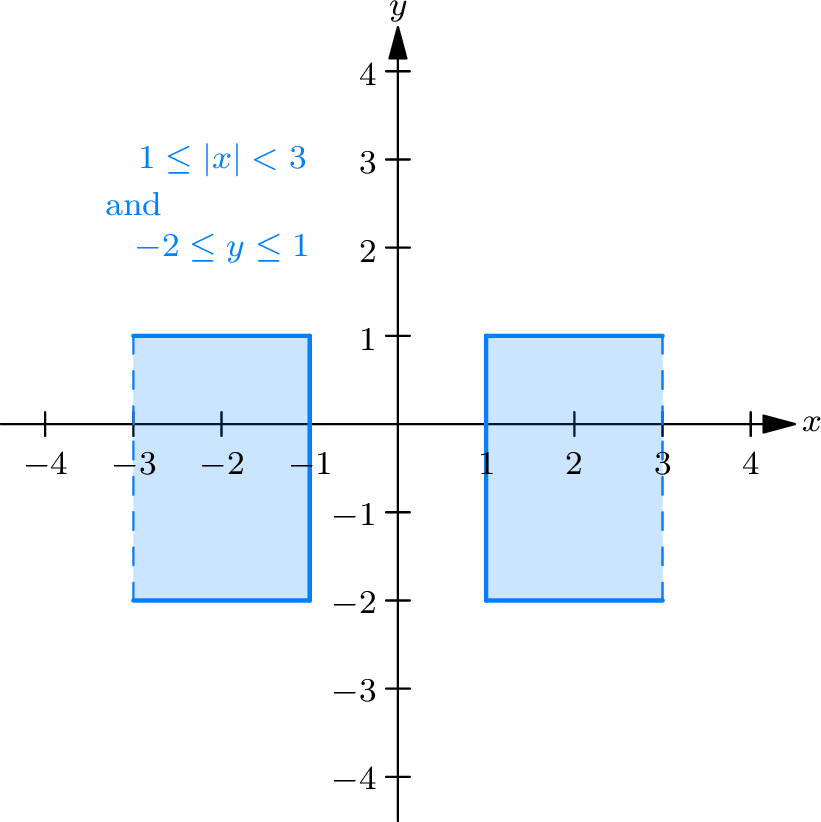
The intersection of these two regions is a pair of rectangular strips in the \(xy\) -plane:
- One strip lies between \(x = -3\) and \(x = -1\) (excluding \(x = -1\) ), and between \(y = -2\) and \(y = 1\) (including the boundaries).
- The other strip lies between \(x = 1\) and \(x = 3\) (excluding \(x = 1\) ), and between \(y = -2\) and \(y = 1\) (including the boundaries).
The final region satisfying both inequalities is shown shaded below. It consists of two disjoint rectangular regions, with dashed boundaries at \(x = -1\) and \(x = 1\) to indicate the excluded lines.
Distance Between Points
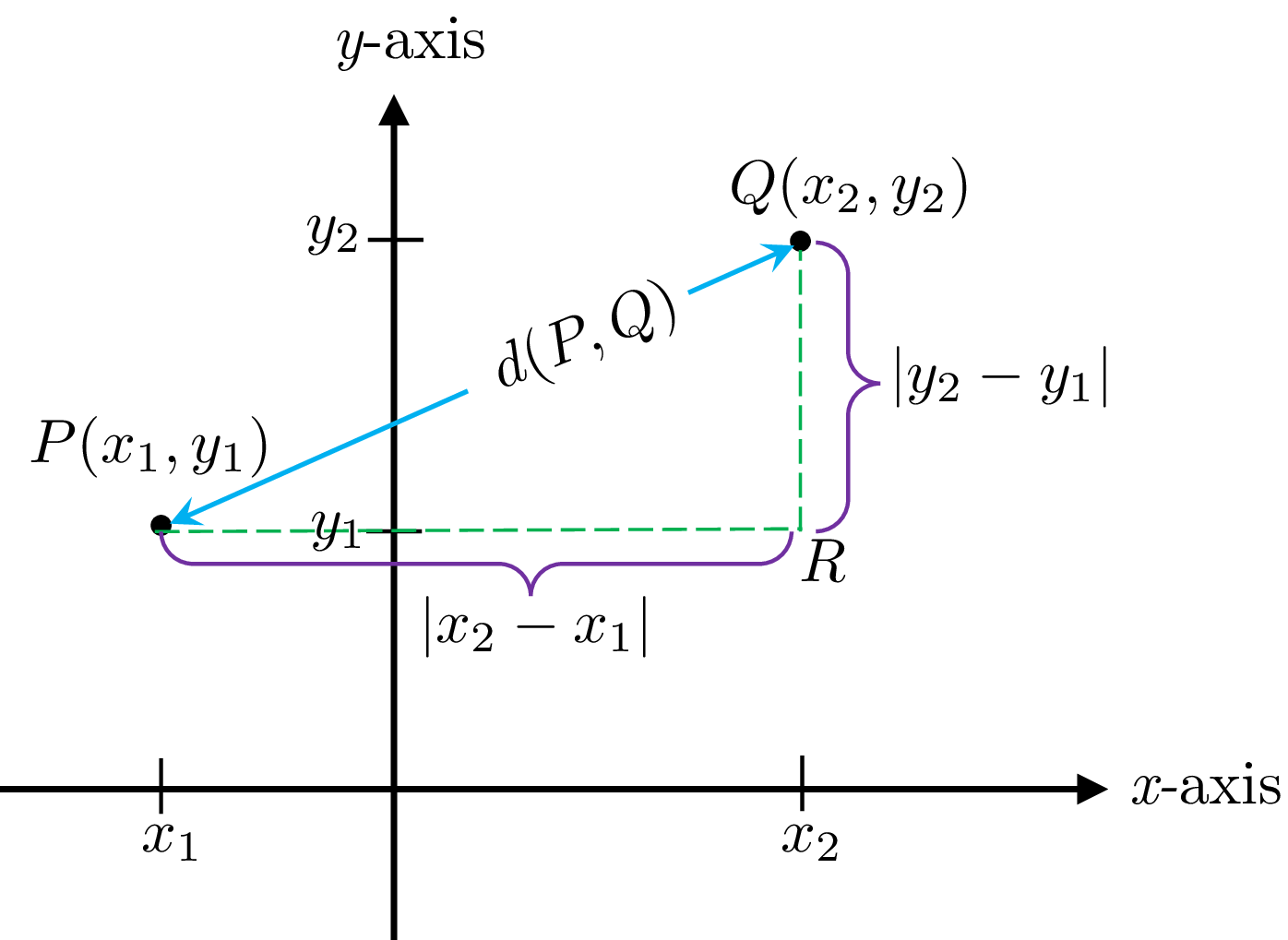
Because we used the same unit of length on both axes, we can apply geometry to express the distance between two points in terms of their coordinates. Consider two points \(P(x_{1},y_{1})\) and \(Q(x_{2},y_{2})\) as in the following figure . If we apply the Pythagorean theorem to the right triangle \(PRQ\) , we realize the distance between \(P\) and \(Q\) , denoted by \(d(P,Q)\) or \(|PQ|\) is given by: \[\begin{align} |PQ|=&\sqrt{|PR|^2+|RQ|^2}\\ =&\sqrt{|x_2-x_1|^2+|y_2-y_1|^2} \end{align}\]
- Notice \(|a-b|^2=|b-a|^2=(b-a)^2=(a-b)^2\) .
\[\bbox[5px,border:1px solid black;background-color:#f2f2f2]{d(P,Q)=|PQ|=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}\]
Example 4. Find the distance between the points \(P(1,-5)\) and \(Q(-1,3)\) .
Solution
Using the distance formula \[\begin{align} d(P,Q)=|PQ| & =\sqrt{(-1-1)^{2}+(3-(-5))^{2}}\\ & =\sqrt{(-2)^{2}+8^{2}}\\ & =\sqrt{68} \end{align}\]
The Midpoint Formula
The coordinates of the midpoint 1 \(M(x_{m},y_{m})\) of the line segment joining \(P(x_{1},y_{1})\) and \(Q(x_{2},y_{2})\) is \[(x_{m},y_{m})=\left(\frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2}\right)\]
Suppose we have two points \(P(x_1,y_1)\) and \(Q(x_2,y_2)\) , and we want to find a point \(M(x_m,y_m)\) that is equidistant from both points, meaning \(|MP|=|MQ|\) . To find formulas for the coordinates of \(M\) , let’s create two auxiliary points:
- \(N(x_m,y_1)\)
- \(R(x_2,y_m)\)
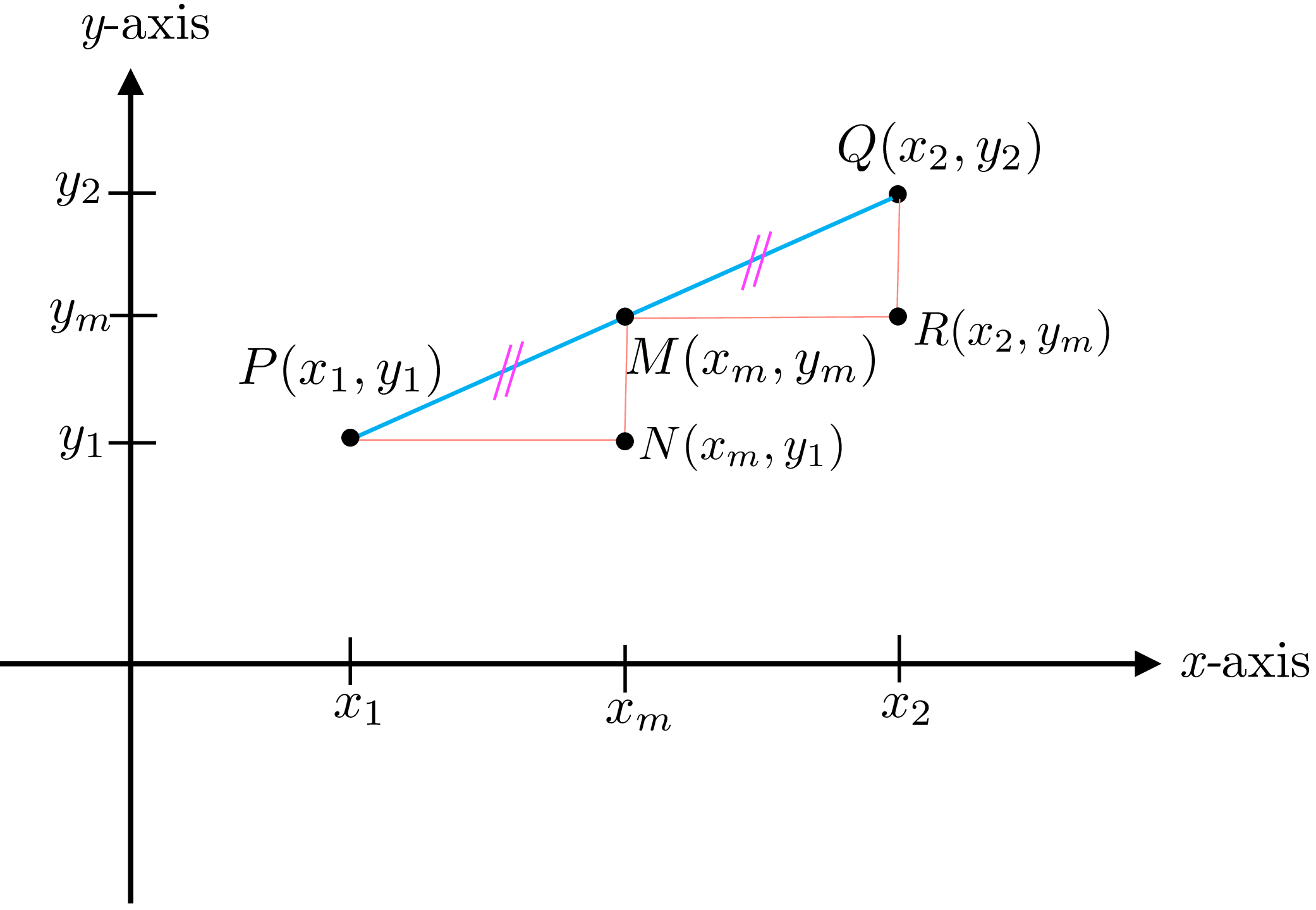
These points form right triangles \(PNM\) and \(MRQ\) . These triangles are congruent because:
- They share equal angles (corresponding angles are equal)
- By our assumption, \(|MP|=|MQ|\)
Since these triangles are congruent, their corresponding sides must be equal:
- \(|PN|=|MR|\) , which gives us \(x_m-x_1=x_2-x_m\)
- \(|MN|=|QR|\) , which gives us \(y_m-y_1=y_2-y_m\)
From the first equation ( \(x_m-x_1=x_2-x_m\) ): \[2x_m=x_1+x_2 \implies x_m=\frac{x_1+x_2}{2}\]
From the second equation ( \(y_m-y_1=y_2-y_m\) ): \[2y_m=y_1+y_2 \implies y_m=\frac{y_1+y_2}{2}\]
These formulas give us the coordinates of the midpoint \(M\) .
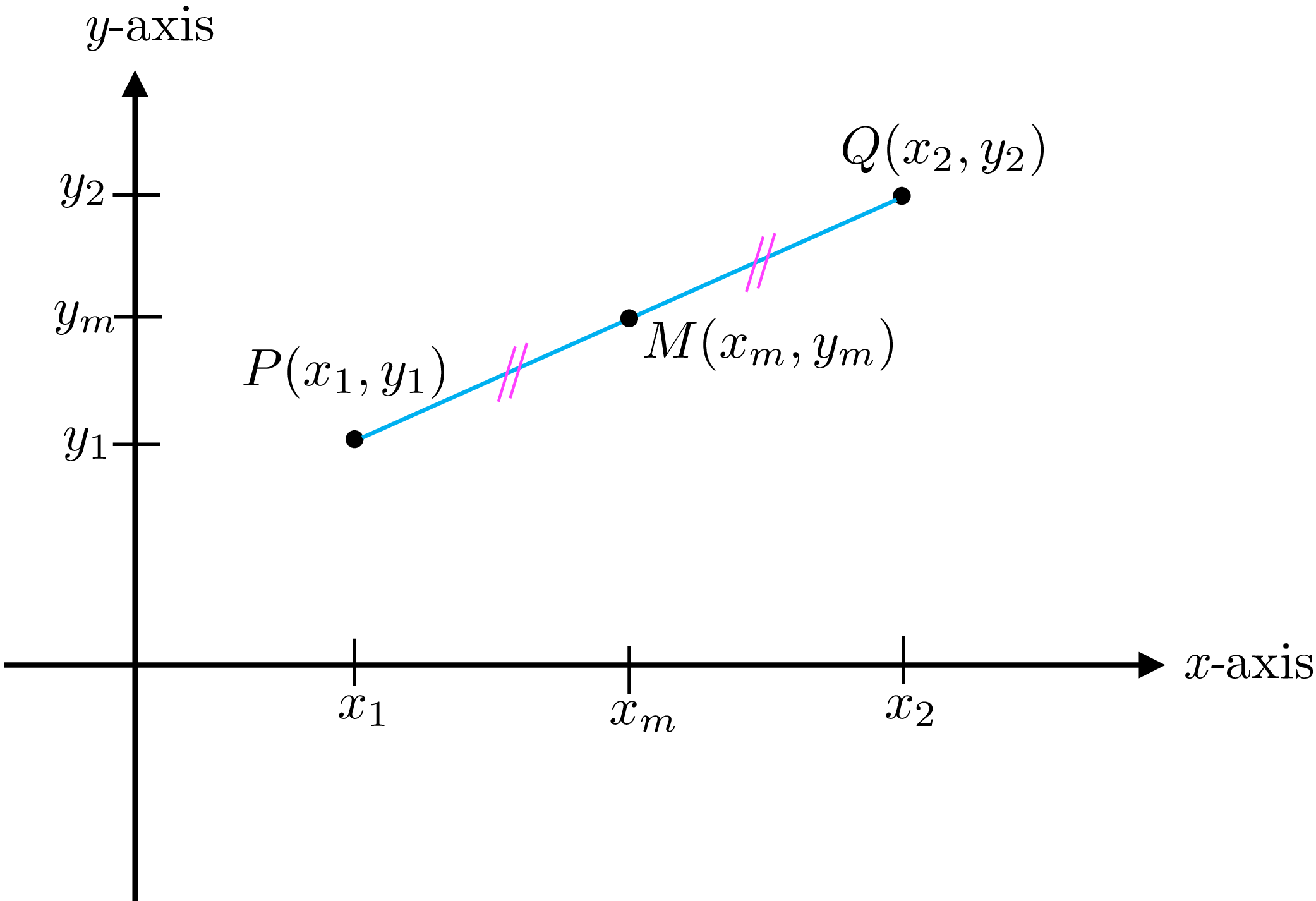
Example 5. Find the midpoint of the line segment with endpoints \((-3,1.5)\) and \((7,-4.5)\) .
Solution
Using the formula, the coordinates of the midpoint are \[\begin{align} \left(\frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2}\right) & =\left(\frac{-3+7}{2},\frac{1.5-4.5}{2}\right)\\ & =\left(2,-1.5\right) \end{align}\]
- A point that divides the line segment into two equal parts; that is \(|MP|=|MQ|\) . ↩︎