Sens géométrique de la dérivation

Il est utile de considérer quelle signification géométrique peut être donnée à la dérivée.

En premier lieu, toute fonction de \(x\), telle, par exemple, que \(x^2\), ou \(\sqrt{x}\), ou \(ax+b\), peut être tracée sous forme de courbe ; et de nos jours, de nombreux étudiants sont familiers avec le processus de traçage de courbes. Divers outils sont disponibles pour tracer des courbes, tels que les calculatrices graphiques, Wolfram Alpha,¹ MATLAB, Python, ou même Microsoft Excel.

Soit \(PQR\), dans la figure suivante, une portion d'une courbe tracée par rapport aux axes \(x\) et \(y\). Considérons un point quelconque \(Q\) sur cette courbe avec les coordonnées \((x,y)\) (c'est-à-dire que l'abscisse du point est \(x\) et son ordonnée est \(y\)).

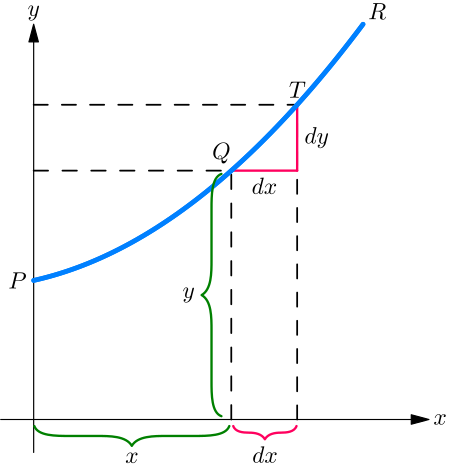
Observons maintenant comment \(y\) change lorsque \(x\) varie. Si \(x\) est augmenté d'un petit incrément \(dx\), vers la droite, on observera que \(y\) aussi (dans cette courbe particulière) augmente d'un petit incrément \(dy\) (parce que cette courbe particulière se trouve être une courbe ascendante). Alors le rapport de \(dy\) à \(dx\) est une mesure du degré d'inclinaison de la courbe entre les deux points \(Q\) et \(T\). En fait, on peut voir sur la figure que la courbe entre \(Q\) et \(T\) a de nombreuses pentes différentes, de sorte que nous ne pouvons pas très bien parler de la pente de la courbe entre \(Q\) et \(T\). Si, cependant, \(Q\) et \(T\) sont si proches l'un de l'autre que la petite portion \(QT\) de la courbe est pratiquement droite, alors il est vrai de dire que le rapport \(\dfrac{dy}{dx}\) est la pente de la courbe le long de \(QT\). La droite \(QT\) prolongée de chaque côté touche la courbe uniquement le long de la portion \(QT\), et si cette portion est indéfiniment petite, la droite touchera la courbe en pratiquement un seul point, et sera donc une tangente à la courbe.

Cette tangente à la courbe a évidemment la même pente que \(QT\), de sorte que \(\boldsymbol{\dfrac{dy}{dx}}\) est la pente de la tangente à la courbe au point \(Q\) pour lequel la valeur de \(\boldsymbol{\dfrac{dy}{dx}}\) est trouvée.

Nous avons vu que l'expression courte « la pente d'une courbe » n'a pas de signification précise, car une courbe a tant de pentes — en fait, chaque petite portion d'une courbe a une pente différente. « La pente d'une courbe en un point » est, cependant, une chose parfaitement définie ; c'est la pente d'une très petite portion de la courbe située juste à ce point ; et nous avons vu que c'est la même chose que « la pente de la tangente à la courbe en ce point ».

La pente d'une courbe en un point est la pente de la tangente à la courbe en ce point.

Observez que \(dx\) est un petit pas vers la droite, et \(dy\) le petit pas correspondant vers le haut. Ces pas doivent être considérés comme aussi courts que possible — en fait indéfiniment courts — bien que dans les diagrammes nous devions les représenter par des morceaux qui ne sont pas infiniment petits, sinon ils ne pourraient pas être vus.

Nous ferons par la suite un usage considérable de cette circonstance que \(\boldsymbol{\dfrac{dy}{dx}}\) représente la pente de la courbe en tout point.

Si une courbe monte à \(45^\circ\) en un point particulier, comme dans la figure suivante, \(dy\) et \(dx\) seront égaux, et la valeur de \(\dfrac{dy}{dx} = 1\).

Si la courbe monte plus raide que \(45^\circ\) (figure suivante), \(\dfrac{dy}{dx}\) sera supérieure à \(1\).

Si la courbe monte très doucement, comme dans la figure suivante, \(\dfrac{dy}{dx}\) sera une fraction inférieure à \(1\).

Pour une ligne horizontale, ou un endroit horizontal dans une courbe, \(dy=0\), et par conséquent \(\dfrac{dy}{dx}=0\).

Si une courbe descend vers le bas, comme dans la figure suivante, \(dy\) sera un pas vers le bas, et doit donc être considérée comme de valeur négative ; par conséquent \(\dfrac{dy}{dx}\) aura également un signe négatif.

Si la « courbe » s'avère être une ligne droite, comme celle de la figure suivante, la valeur de \(\dfrac{dy}{dx}\) sera la même en tous points le long de celle-ci. En d'autres termes, sa pente est constante.

Si une courbe est une qui tourne davantage vers le haut à mesure qu'elle avance vers la droite, les valeurs de \(\dfrac{dy}{dx}\) deviendront de plus en plus grandes avec l'augmentation de la raideur, comme dans la figure suivante.

Si une courbe est une qui devient de plus en plus plate à mesure qu'elle avance, les valeurs de \(\dfrac{dy}{dx}\) deviendront de plus en plus petites à mesure que la partie plus plate est atteinte, comme dans la figure suivante.

Si une courbe descend d'abord, puis remonte, comme dans la figure suivante, présentant une concavité vers le haut, alors clairement \(\dfrac{dy}{dx}\) sera d'abord négative, avec des valeurs diminuant à mesure que la courbe s'aplatit, puis sera nulle au point où le fond du creux de la courbe est atteint ; et à partir de ce point \(\dfrac{dy}{dx}\) aura des valeurs positives qui ne cesseront d'augmenter. Dans un tel cas, \(y\) est dit passer par un minimum. La valeur minimale de \(y\) n'est pas nécessairement la plus petite valeur de \(y\), c'est cette valeur de \(y\) correspondant au fond du creux ; par exemple, dans la figure suivante, la valeur de \(y\) correspondant au fond du creux est \(1\), tandis que \(y\) prend ailleurs des valeurs qui sont plus petites que celle-ci. La caractéristique d'un minimum est que \(y\) doit augmenter de chaque côté de celui-ci.

Note—Pour la valeur particulière de \(x\) qui rend \(y\) un minimum, la valeur de \(\dfrac{dy}{dx} = 0\).

Si une courbe monte d'abord puis descend, les valeurs de \(\dfrac{dy}{dx}\) seront d'abord positives ; puis nulles, lorsque le sommet est atteint ; puis négatives, lorsque la courbe descend, comme dans la figure suivante. Dans ce cas \(y\) est dit passer par un maximum, mais la valeur maximale de \(y\) n'est pas nécessairement la plus grande valeur de \(y\). Dans la figure ci-dessus, le maximum de \(y\) est \(2\frac{1}{3}\), mais ce n'est en aucun cas la plus grande valeur que \(y\) puisse avoir en un autre point de la courbe.

Note—Pour la valeur particulière de \(x\) qui rend \(y\) un maximum, la valeur de \(\dfrac{dy}{dx}= 0\).

Si une courbe a la forme particulière de la figure suivante, les valeurs de \(\dfrac{dy}{dx}\) seront toujours positives ; mais il y aura un endroit particulier où la pente est la moins raide, où la valeur de \(\dfrac{dy}{dx}\) sera un minimum ; c'est-à-dire, inférieure à ce qu'elle est en toute autre partie de la courbe.

Si une courbe a la forme de la figure suivante, la valeur de \(\dfrac{dy}{dx}\) sera négative dans la partie supérieure et positive dans la partie inférieure ; tandis qu'au nez de la courbe, où elle devient réellement perpendiculaire, la valeur de \(\dfrac{dy}{dx}\) sera infiniment grande.

En résumé :

Quand \(x\) augmente

Si \(\dfrac{dy}{dx}>0\), \(\qquad y\) augmente ; la courbe monte vers la droite.

Si \(\dfrac{dy}{dx}<0\), \(\qquad y\) diminue ; la courbe descend vers la droite.

Maintenant que nous comprenons que \(\dfrac{dy}{dx}\) mesure la raideur d'une courbe en tout point, tournons-nous vers certaines des équations que nous avons déjà appris à différencier.

Exemple 10.1. Comme cas le plus simple, prenons ceci : \[y=x+b.\]

Elle est tracée dans la figure suivante, en utilisant des échelles égales pour \(x\) et \(y\). Si nous posons \(x = 0\), alors l'ordonnée correspondante sera \(y = b\) ; c'est-à-dire que la « courbe » traverse l'axe des \(y\) à la hauteur \(b\). De là, elle monte à \(45^\circ\) ; car quelles que soient les valeurs que nous donnons à \(x\) vers la droite, nous avons un \(y\) égal à monter. La ligne a un gradient de \(1\) sur \(1\).

Maintenant, différencions \(y = x+b\), selon les règles que nous avons déjà apprises, et nous obtenons \(\dfrac{dy}{dx} = 1\).

La pente de la ligne est telle que pour chaque petit pas \(dx\) vers la droite, nous faisons un petit pas égal \(dy\) vers le haut. Et cette pente est constante — toujours la même pente.

Exemple 10.2. Prenons un autre cas : \[y = ax+b.\] Nous savons que cette courbe, comme la précédente, partira d'une hauteur \(b\) sur l'axe des \(y\). Mais avant de tracer la courbe, trouvons sa pente en la différenciant ; ce qui donne \(\dfrac{dy}{dx} = a\). La pente sera constante, à un angle dont la tangente est ici appelée \(a\). Attribuons à \(a\) une valeur numérique — disons \(\frac{1}{3}\). Alors nous devons lui donner une pente telle qu'elle monte de \(1\) sur \(3\) ; ou \(dx\) sera \(3\) fois plus grand que \(dy\) ; comme agrandi dans la figure suivante.

Alors, tracez la ligne dans la figure suivante avec cette pente.

Passons maintenant à un cas légèrement plus difficile.

Exemple 10.3. Soit \[y= ax^2 + b.\]

Encore une fois, la courbe commencera sur l'axe des \(y\) à une hauteur \(b\) au-dessus de l'origine.

Maintenant, différencions. [Si vous avez oublié, revenez en arrière; ou, plutôt, ne revenez pas en arrière, mais réfléchissez à la différenciation.] \[\frac{dy}{dx} = 2ax.\]

Cela montre que la pente ne sera pas constante : elle augmente à mesure que \(x\) augmente. Au point de départ \(P\), où \(x = 0\), la courbe (figure suivante) n'a pas de pente — c'est-à-dire qu'elle est horizontale. À gauche de l'origine, où \(x\) a des valeurs négatives, \(\dfrac{dy}{dx}\) aura également des valeurs négatives, ou descendra de gauche à droite, comme dans la Figure.

Illustrons cela en travaillant sur un cas particulier. En prenant l'équation \[y = \frac{1}{4}x^2 + 3,\] et en la différenciant, nous obtenons \[\dfrac{dy}{dx} = \frac{1}{2}x.\] Maintenant, attribuons quelques valeurs successives, disons de \(0\) à \(5\), à \(x\); et calculons les valeurs correspondantes de \(y\) par la première équation ; et de \(\dfrac{dy}{dx}\) par la deuxième équation. En tabulant les résultats, nous avons :

\(x\)	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)
\(y\)	\(3\)	\(3\frac{1}{4}\)	\(4\)	\(5\frac{1}{4}\)	\(7\)	\(9\frac{1}{4}\)
\(\dfrac{dy}{dx}\)	\(0\)	\(\frac{1}{2}\)	\(1\)	\(1\frac{1}{2}\)	\(2\)	\(2\frac{1}{2}\)

Tracez-les ensuite en deux courbes, Fig. 10.18 et Fig. 10.19 ; dans la Fig. 10.18 en traçant les valeurs de \(y\) par rapport à celles de \(x\) et dans la Fig. 10.19 celles de \(\dfrac{dy}{dx}\) par rapport à celles de \(x\). Pour toute valeur assignée de \(x\), la hauteur de l'ordonnée dans la deuxième courbe est proportionnelle à la pente de la première courbe.

Si une courbe présente un point de rebroussement soudain, comme dans la figure suivante, la pente à ce point change brusquement d'une pente ascendante à une pente descendante. Dans ce cas, \(\dfrac{dy}{dx}\) subira clairement un changement abrupt d'une valeur positive à une valeur négative.

Les exemples suivants montrent d'autres applications des principes qui viennent d'être expliqués.

Exemple 10.4. (a) Trouver la pente de la tangente à la courbe \[y = \frac{1}{2x} + 3,\] au point où \(x = -1\). (b) Trouver l'angle que cette tangente forme avec la courbe \(y = 2x^2 + 2\).

Solution. (a) La pente de la tangente est la pente de la courbe au point où elles se touchent ; c'est-à-dire, c'est le \(\dfrac{dy}{dx}\) de la courbe pour ce point. Ici \(\dfrac{dy}{dx} = -\dfrac{1}{2x^2}\) et pour \(x = -1\), \(\dfrac{dy}{dx} = -\dfrac{1}{2}\), qui est la pente de la tangente et de la courbe en ce point. La tangente, étant une ligne droite, a pour équation \(y = ax + b\), et sa pente est \(\dfrac{dy}{dx} = a\), donc \(a = -\dfrac{1}{2}\). Aussi si \(x= -1\), \(y = \dfrac{1}{2(-1)} + 3 = 2\frac{1}{2}\) ; et comme la tangente passe par ce point, les coordonnées du point doivent satisfaire l'équation de la tangente, à savoir \[y = -\dfrac{1}{2} x + b,\] de sorte que \(2\frac{1}{2} = -\dfrac{1}{2} \times (-1) + b\) et \(b = 2\) ; l'équation de la tangente est donc \(y = -\dfrac{1}{2} x + 2\) (voir la figure suivante).

(b) Maintenant, lorsque deux courbes se rencontrent, l'intersection étant un point commun aux deux courbes, ses coordonnées doivent satisfaire l'équation de chacune des deux courbes ; c'est-à-dire, elle doit être une solution du système d'équations simultanées formé en couplant les équations des courbes. Ici, les courbes se rencontrent en des points donnés par la solution de \[\left\{ \begin{align} y &= 2x^2 + 2, \\ y &= -\frac{1}{2} x + 2 \quad\text{or}\quad 2x^2 + 2 = -\frac{1}{2} x + 2; \end{align} \right.\]

c'est-à-dire, \[x(2x + \frac{1}{2}) = 0.\]

Cette équation a pour solutions \(x = 0\) et \(x = -\frac{1}{4}\) (voir la figure suivante). La pente de la courbe \(y = 2x^2 + 2\) en tout point est \[\dfrac{dy}{dx} = 4x.\]

Pour le point où \(x = 0\), cette pente est nulle ; la courbe est horizontale. Pour le point où \[x = -\dfrac{1}{4},\quad \dfrac{dy}{dx} = -1;\] par conséquent, la courbe en ce point descend vers la droite selon un angle \(\theta\) avec l'horizontale tel que \(\tan \theta = 1\) ; c'est-à-dire, à \(45^\circ\) par rapport à l'horizontale.

La pente de la ligne droite est \(-\frac{1}{2}\) ; c'est-à-dire, elle descend vers la droite et forme avec l'horizontale un angle \(\phi\) tel que \(\tan \phi = \frac{1}{2}\) ; c'est-à-dire, un angle de \(26^\circ~34'\). Il s'ensuit qu'au premier point, la courbe coupe la ligne droite sous un angle de \(26^\circ~34'\), tandis qu'au second, elle la coupe sous un angle de \(45^\circ - 26^\circ~34' = 18^\circ~26'\) (voir la figure suivante).

Exemple 10.5. Une ligne droite doit être tracée, passant par un point dont les coordonnées sont \(x = 2\), \(y = -1\), comme tangente à la courbe \(y = x^2 - 5x + 6\). Trouver les coordonnées du point de contact.
Note.—-le point \((2,-1)\) ne se trouve pas sur la courbe \(y=x^2-5x+6\).

Solution. La pente de la tangente doit être la même que le \(\dfrac{dy}{dx}\) de la courbe ; c'est-à-dire, \(2x - 5\).

L'équation de la ligne droite est \(y = ax + b\), et comme elle est satisfaite pour les valeurs \(x = 2\), \(y = -1\), alors \(-1 = a\times2 + b\) ; aussi, son \(\dfrac{dy}{dx} = a = 2x - 5\) [puisque \(y=ax+b\) est la ligne tangente, sa pente, \(a\), doit être la même que \(\dfrac{d(x^2-5x+6)}{dx}\)].

Le \(x\) et le \(y\) du point de contact doivent également satisfaire à la fois l'équation de la tangente et l'équation de la courbe.

Nous avons alors \[\left\{\begin{align} y &= x^2 - 5x + 6, &&\text{(i)} \\ y &= ax + b, &&\text{(ii)} \\ -1 &= 2a + b, &&\text{(iii)} \\ a &= 2x - 5, &&\text{(iv)} \end{align}\right.\] quatre équations en \(a\), \(b\), \(x\), \(y\).

Les équations (i) et (ii) donnent \(x^2 - 5x + 6 = ax+b\).

En remplaçant \(a\) et \(b\) par leur valeur dans celle-ci, nous obtenons \[x^2 - 5x + 6 = (2x - 5)x - 1 - 2(2x - 5),\] qui se simplifie en \(x^2 - 4x + 3 = 0\), dont les solutions sont : \(x = 3\) et \(x = 1\). En remplaçant dans (i), nous obtenons \(y = 0\) et \(y = 2\) respectivement ; les deux points de contact sont alors \(x = 1\), \(y = 2\), et \(x = 3\), \(y = 0\) (voir la figure suivante).

Note.—Dans tous les exercices traitant des courbes, les étudiants trouveront extrêmement instructif de vérifier les déductions obtenues en traçant réellement les courbes.

Exercices

Exercice 10.1. Tracez la courbe \(y = \dfrac{3}{4} x^2 - 5\), en utilisant des échelles égales pour \(x\) et \(y\). Mesurez aux points correspondant à différentes valeurs de \(x\), l'angle de sa pente.

Trouvez, en différentiant l'équation, l'expression de la pente ; et voyez, à partir d'une Table de Tangentes Naturelles, si cela concorde avec l'angle mesuré.

Solution

\[y=\frac{3}{4} x^2 - 5 \Rightarrow \frac{dy}{dx}=\frac{3}{2}x\]

Quand \(x=-3\), \(\dfrac{dy}{dx}=-\dfrac{9}{2}\)
d'après le graphique : pente de la tangente \(=\dfrac{-9}{2}=-4.5\). Ils concordent.

Quand \(x=-2\), \(\dfrac{dy}{dx}=-3\)
d'après le graphique : pente de la tangente \(=\dfrac{-6}{2}=-3\). Ils concordent.

Quand \(x=-1\), \(\dfrac{dy}{dx}=-\dfrac{3}{2}\)
d'après le graphique : pente de la tangente \(=\dfrac{-3}{2}=-1.5\). Ils concordent.

Quand \(x=0\), \(\dfrac{dy}{dx}=0\)
d'après le graphique : la tangente est horizontale. Sa pente est donc nulle. Ils concordent.

Quand \(x=1\), \(\dfrac{dy}{dx}=\dfrac{3}{2}\)
d'après le graphique : pente de la tangente \(=\dfrac{3}{2}=1.5\). Ils concordent.

Quand \(x=2\), \(\dfrac{dy}{dx}=3\)
d'après le graphique : pente de la tangente \(=\dfrac{6}{2}=3\). Ils concordent.

Quand \(x=3\), \(\dfrac{dy}{dx}=\dfrac{9}{2}\)
d'après le graphique : pente de la tangente \(=\dfrac{9}{2}=4.5\). Ils concordent.

Exercice 10.2. Trouvez quelle sera la pente de la courbe \[y = 0.12x^3 - 2,\] au point particulier avec \(x=2\).

Réponse

\(1.44\).

Solution

\[\begin{align} & y=0.12 x^{3}-2 \\ & \frac{d y}{d x}=3 \times 0.12 x^{2}=0.36 x^{2} \end{align}\]

Quand \(x=2, \quad \dfrac{d y}{d x}=1.44\).

Par conséquent, la pente de la courbe au point avec \(x=2\) est \(1.44\).

Exercice 10.3. Si \(y = (x - a)(x - b)\), montrez qu'au point particulier de la courbe où \(\dfrac{dy}{dx} = 0\), \(x\) aura la valeur \(\frac{1}{2} (a + b)\).

Solution

\[y=(x-a)(x-b)\] En utilisant la règle du produit : \[\begin{align} \frac{d y}{d x}&=(x-b)+(x-a)\\ &=2 x-a-b \end{align}\] En posant \(\dfrac{dy}{dx}=0\), nous obtenons \[x=\frac{a+b}{2}.\]\]

Exercice 10.4. Trouvez le \(\dfrac{dy}{dx}\) de l'équation \(y = x^3 + 3x\); et calculez les valeurs numériques de \(\dfrac{dy}{dx}\) pour les points correspondant à \(x = 0\), \(x = \frac{1}{2}\), \(x = 1\), \(x = 2\).

Réponse

\(\dfrac{dy}{dx} = 3x^2 + 3\); et les valeurs numériques sont : \(3\), \(3 \frac{3}{4}\), \(6\), et \(15\).

Solution

\[\begin{align} & y=x^{3}+3 x \\ & \frac{d y}{d x}=3 x^{2}+3 \end{align}\]

Quand \(x=0\), \(\dfrac{dy}{dx}=3\).

Quand \(x=0\), \(\dfrac{dy}{dx}=3+\frac{3}{4}=3\frac{3}{4}=3.75\).

Quand \(x=1\), \(\dfrac{dy}{dx}=6\).

Quand \(x=2\), \(\dfrac{dy}{dx}=15\).

Exercice 10.5. Dans la courbe dont l'équation est \(x^2 + y^2 = 4\), trouvez les valeurs de \(x\) aux points où la pente \({} = 1\).

Réponse

\(\pm \sqrt{2}\).

Solution

\[x^{2}+y^{2}=4\] Résolvons pour \(y\): \[y= \pm \sqrt{4-x^{2}}= \pm\left(4-x^{2}\right)^{\frac{1}{2}}\]

Pour trouver \(\dfrac{dy}{dx}\), soit \(u=4-x^{2}\). Alors \(y= \pm u^{\frac{1}{2}}\) et

\[\begin{align} \frac{d y}{d x} & =\frac{d y}{d u} \cdot \frac{d u}{d x} \\ & = \pm \frac{1}{2} u^{-\frac{1}{2}}(-2 x) \\ & = \pm \frac{-x}{\sqrt{4-x^{2}}}=\mp \frac{x}{\sqrt{4-x^{2}}} \\ \frac{d y}{d x} & =1 \Rightarrow \mp \frac{x}{\sqrt{4-x^{2}}}=1 \end{align}\]

Considérons d'abord le \(-\) signe :

\[-x=\sqrt{4-x^{2}}\]

Nous devons avoir \(x \leq 0\) car le membre de droite est non négatif.

\[\begin{align} & x^{2}=4-x^{2} \\ & 2 x^{2}=4 \\ & x= \pm \sqrt{2} \end{align}\] Seul \(x=-\sqrt{2}\) est acceptable.

Quand \(x=-\sqrt{2}\) :

\[y=+\sqrt{4-x^{2}}=+\sqrt{2}\]

Considérons maintenant le \(+\) signe :

\[x=\sqrt{4-x^{2}}\] Nous devons avoir \(x \geq 0\) car le membre de droite est toujours non négatif

\[\begin{align} x^{2} & =4-x^{2} \\ 2 x^{2} & =4 \\ x & = \pm \sqrt{2} \end{align}\] Seul \(x=+\sqrt{2}\) est acceptable.

Quand \(x=+\sqrt{2}\) : \[y=-\sqrt{4-x^{2}}=-\sqrt{2}\]

Par conséquent, en deux points \((-\sqrt{2},+\sqrt{2})\) et \((+\sqrt{2},-\sqrt{2})\), la pente de la courbe est 1.

Exercice 10.6. Trouvez la pente, en tout point, de la courbe dont l'équation est \(\dfrac{x^2 }{3^2} + \dfrac{y^2}{2^2} = 1\); et donnez la valeur numérique de la pente à l'endroit où \(x = 0\), et à celui où \(x = 1\).

Réponse

\(\dfrac{dy}{dx} = - \dfrac{4}{9} \dfrac{x}{y}\). La pente est nulle là où \(x = 0\); et est \(\mp \dfrac{1}{3 \sqrt{2}}\) où \(x = 1\).

Solution

\[\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\]

Méthode 1 : Utilisation de la règle de la chaîne

\[\begin{align} & \frac{d\left(\frac{x^{2}}{9}\right)}{d x}+\frac{d\left(\frac{y^{2}}{4}\right)}{d x}=1 \\ & \frac{1}{9} 2 x+\frac{1}{4} 2 y \cdot \frac{d y}{d x}=0 \\ \end{align}\] Donc \[\frac{d y}{d x}=-\frac{\frac{1}{9} x}{\frac{y}{4}}=-\frac{4}{9} \frac{x}{y}\] ou \[\begin{align} \frac{d y}{d x} & =-\frac{4}{9} \frac{x}{ \pm 2 \sqrt{1-\frac{x^{2}}{9}}} \\ & =\mp \frac{2}{3} \frac{x}{\sqrt{9-x^{2}}} \end{align}\]

Méthode 2 : Nous pouvons obtenir le même résultat si nous résolvons \[\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\] pour \(y\). C'est-à-dire

\[\begin{align} y & = \pm 2 \sqrt{1-\frac{x^{2}}{9}} \\ & = \pm 2\left(1-\frac{x^{2}}{9}\right)^{\frac{1}{2}} \end{align}\]

Pour trouver \(\frac{d y}{d x}\), soit \(x=1-\frac{x^{2}}{9}\). Alors \(y= \pm 2 u^{\frac{1}{2}}\) et \[\begin{align} \frac{d y}{d x} & =\frac{d y}{d u} \cdot \frac{d u}{d x} \\ & = \pm \frac{1}{2} u^{-\frac{1}{2}}\cdot(-2 x) \\ & = \pm \frac{-x}{\sqrt{4-x^2}}=\mp \frac{x}{\sqrt{4-x^2}} \end{align}\]

Quand \(x=0, \quad \dfrac{d y}{d x}=0\)

Quand \(x=1, \quad \dfrac{d y}{d x}=\mp \dfrac{2}{3 \sqrt{8}}=\mp \dfrac{1}{3 \sqrt{2}}.\) Pour être plus précis, quand \(x=1\), si \(y>0\), alors \(\dfrac{dy}{dx}=-\dfrac{1}{3\sqrt{2}}\), et si \(y<0\), alors \(\dfrac{dy}{dx}=+\dfrac{1}{3\sqrt{2}}\).

Exercice 10.7. L'équation d'une tangente à la courbe \(y = 5 - 2x + 0.5x^3\), étant de la forme \(y = mx + n\), où \(m\) et \(n\) sont des constantes, trouver la valeur de \(m\) et \(n\) si le point où la tangente touche la courbe a \(x=2\) pour abscisse.

Réponse

\(m = 4\), \(n = -3\).

Solution

\[y=5-2 x+0.5 x^{3}\]

\[\frac{d y}{d x}=-2+1.5 x^{2}\]

Quand \(x=2, \quad \frac{d y}{d x}=4\).

Quand \(x=2, \quad y=5\).

L'équation de la droite de pente 4 passant par \((2,5)\) est \[y-5=4(x-2)\] ou \[y=4 x-3\]\] Par conséquent,

\[m=4 \quad \text { et }\quad n=-3\]

Exercice 10.8. Sous quel angle les deux courbes \[y = 3.5x^2 + 2 \quad \text{et} \quad y = x^2 - 5x + 9.5\] se coupent-elles ?²

Réponse

Intersections à \(x = 1\), \(x = -3\). Angles \(153^\circ\;26'\), \(2^\circ\;28'\).

Solution

Premièrement, nous devons calculer en quel point ces deux courbes se coupent :

En égalisant les équations des deux courbes :

\[3.5 x^{2}+2=x^{2}-5 x+9.5\] \[\Rightarrow 2.5 x^{2}+5 x-7.5=0\] \[\begin{align} \Rightarrow \quad x&=\frac{-5 \pm \sqrt{25+4 \times 2.5 \times 7.5}}{5} \\ &=\frac{-5 \pm 10}{5} \end{align}\]

Par conséquent, ces deux courbes se coupent en \(x=-3\) et \(x=1\).

Maintenant, nous devons trouver les pentes de ces deux courbes en \(x=3\) et \(x=1\).

\[\begin{align} & y=3.5 x^{2}+2 \Rightarrow \frac{d y}{d x}=7 x \\ & y=x^{2}-5 x+9.5 \Rightarrow \frac{d y}{d x}=2 x-5 \end{align}\]

Quand \(x=-3\), la pente de la première courbe est \(-21\) et la pente de la seconde courbe est \(-11\).

C'est-à-dire \(\tan \alpha=-21\) et \(\tan \beta=-11\), où \(\alpha\) et \(\beta\) sont les angles que leurs tangentes forment avec la direction positive de l'axe des \(x\).

\[\begin{gathered} \tan \alpha=-21 \Rightarrow \alpha=\arctan (-21) \approx-1.52 ~\mathrm{rad} \\ \text { ou }\quad \alpha \approx-87.27^{\circ} \\ \tan \beta=-11 \Rightarrow \beta=\arctan (-11) \approx-1.48~ \mathrm{rad}\\ \text { ou }\quad \beta \approx-84.81^{\circ} \end{gathered}\] Par conséquent, l'angle entre elles quand \(x=3\) est \(87.27-84.81=2.47^{\circ}\) ou

\[\text { angle }=2^{\circ}+0.47 \times 60^{\prime} \approx 2^{\circ} 28^{\prime}\]

De même, quand \(x=1\), la pente de la première courbe est \(7\). \[\tan \alpha=7 \Rightarrow \alpha=\arctan 7 \approx 1.429~\mathrm{rad}\] ou \[\alpha \approx 81.87^\circ\]\]

La pente de la seconde courbe est \(-3\). \[\tan \beta=-3 \Rightarrow \beta=\arctan (-3) \approx-1.249~\mathrm{rad}\]\] ou \[\beta \approx-71.57^{\circ}\]\] Par conséquent, l'angle entre elles quand \(x=1\) est \(81.87+71.57=153.44\) ou \[\text { angle }=153^{\circ}+0.44 \times 60^{\prime} \approx 153^{\circ} 26^{\prime}\]\]

Exercice 10.9. Des tangentes à la courbe \(y = \pm \sqrt{25-x^2}\) sont tracées aux points pour lesquels \(x = 3\) et \(x = 4\). Trouver les coordonnées du point d'intersection des tangentes et leur inclinaison mutuelle.

Réponse

Intersection en \(x =\frac{25}{7}\approx 3.57\), \(y=\frac{25}{7}\approx 3.57\). Angle \(16^\circ\;16'\).

Solution

Considérons \(y>0\). Le cas où \(y<0\) peut alors être obtenu par symétrie. \[\begin{align} y & =+\sqrt{25-x^{2}} \\ \frac{d y}{d x} & =\frac{-2 x}{2 \sqrt{25-x^{2}}}=\frac{-x}{\sqrt{25-x^{2}}} \end{align}\]

Quand \(x=3, \quad \dfrac{d y}{d x}=\frac{-3}{4}\).

Quand \(x=3,\quad y=4\).

L'équation de la tangente au point \(x=3\) et \(y>0\) est alors \[y-4=-\frac{3}{4}(x-3)\] ou \[y=-\frac{3}{4} x+\frac{25}{4}\]

Quand \(x=4,\quad \dfrac{d y}{d x}=-\frac{4}{3}\).

Quand \(x=4,\quad y=3\).

L'équation de la tangente est

\[y-3=-\frac{4}{3}(x-4)\] ou \[y=-\frac{4}{3} x+\frac{25}{3}\]

Pour trouver l'intersection des tangentes aux points \(x=3\) et \(x=4\) (pour \(y>0\)), nous égalisons les équations de ces deux tangentes :

\[\begin{align} -\frac{3}{4} x+\frac{25}{4} & =-\frac{4}{3} x+\frac{25}{3} \\ \Rightarrow\ \frac{7}{12} x & =\frac{25}{12} \\ \Rightarrow\ x & =\frac{25}{7} \approx 3.57 \end{align}\]

Quand \(x=\frac{25}{7}, y=-\frac{3}{4} \times \frac{25}{7}+\frac{25}{4}=\frac{25}{7} \approx 3.57\). Par conséquent, ces deux tangentes se coupent au point \((\frac{25}{7},\frac{25}{7})\approx (3.57, 3.57)\).

Puisque la pente de la première tangente est \(-3/4\), la pente de l'angle qu'elle forme avec l'axe des \(x\)-positifs est \[\alpha=\arctan \left(-\frac{3}{4}\right) \approx-0.643 \text { rad }\] ou \[\alpha \approx-36.87^{\circ}\] De même, la pente de la deuxième tangente est \(-\frac{4}{3}\) et donc l'angle qu'elle forme avec l'axe des \(x\)-positifs est \[\beta=\arctan\left(-\frac{4}{3}\right)\approx -0.927~\text{rad}\] ou \[\beta\approx -53.13^\circ\]

Par conséquent, l'angle entre elles est de \(53.13^{\circ}-36.87^{\circ}=16.26^{\circ}\) ou \[16^{\circ}+0.26 \times 60^{\prime} \approx 16^{\circ} 16^{\prime}\]

Exercice 10.10. Une droite \(y = 2x - b\) touche une courbe \(y = 3x^2 + 2\) en un point. Quelles sont les coordonnées du point de contact, et quelle est la valeur de \(b\)?

Réponse

\(x = \frac{1}{3}\), \(y = 2 \frac{1}{3}\), \(b = -\frac{5}{3}\).

Solution

La pente de \(y=2 x-b\) est 2. Nous devons trouver en quel point la pente de la tangente à \(y=3 x^{2}+2\) est \(2\), nous dérivons \(y=3x^2+2\)

\[\frac{d y}{d x}=6 x=2 \Rightarrow x=\frac{1}{3}\] Quand \(x=\frac{1}{3}, \quad y=3 \times \frac{1}{3^{2}}+2=\frac{7}{3}\).

Par conséquent, le point de contact est \(\left(\frac{1}{3}, \frac{7}{3}\right)\).

L'équation de la tangente en ce point est donc \[y-\frac{7}{3}=2\left(x-\frac{1}{3}\right)\] ou \[y=2 x+\frac{5}{3}\]

Par conséquent \[b=-\frac{5}{3}\]

Sens géométrique de la dérivation

Exercices

footer_h_1

footer_social_media