From the examples of the previous section it will be seen that the advantage of the principle of virtual displacement lies in the over-all view which it gives us of the relationships of the external forces of a system. This principle will enable us in many cases to arrive at definite conclusions concerning the external forces acting on certain structures or machines, without a complete knowledge of the details of the arrangement. Suppose, for example, that we have a box with two levers protruding, as is indicated in Fig. 1.

We apply two vertical forces to the levers as shown in Fig. 1, and we wish to know the relationship between the forces at equilibrium. If we find experimentally that a vertically downward movement of the left-hand lever of \(\delta y_{1}\) produces a vertically upward movement of the right-hand lever of the amount \(\delta y_{2}\), we can immediately say \[ F_{1} \delta y_{1}-F_{2} \delta y_{2}=0 ; \quad \frac{F_{1}}{F_{2}}=\frac{\delta y_{2}}{\delta y_{1}} \]
Thus we can find the relationship between the external forces while remaining in complete ignorance as to the details of the arrangement within the box.
3.4.1 PROBLEMS
1. Two weights rest on frictionless inclined planes as shown in the figure. They are connected by a perfectly flexible, inextensible cord passing over a frictionless pulley. If \(W_{2}\) weighs \(150 \mathrm{lb}\), find, by the principle of virtual displacements, the magnitude of \(W_{1}\) for equilibrium of the system. As a comparison of the two methods, check this problem by writing the usual equations of equilibrium.
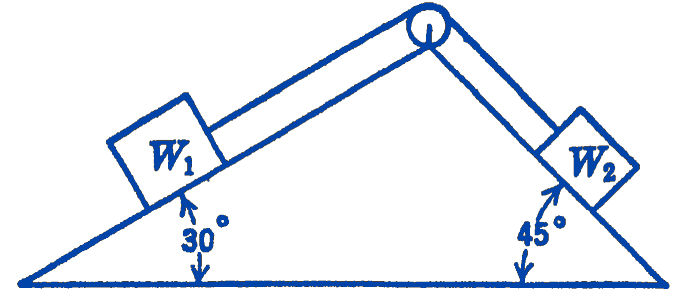
Answer
212 lb
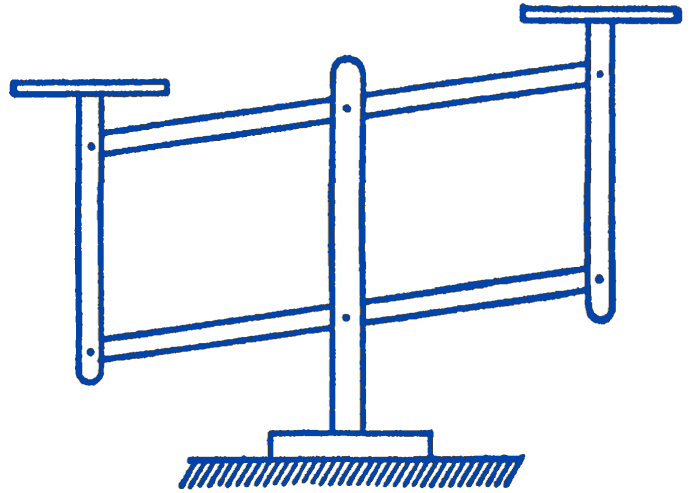
2. Show that a balance constructed as shown in the figure (Roberval’s Balance) will give correct weight independent of the position of the weights on the scale pans.
3. A platform scale is to be designed so that a weight \(W\) can be held in equilibrium by a weight \(W_{b}\). How should the scales be constructed so that the readings will be independent of the position \(x\) of the weight on the platform?
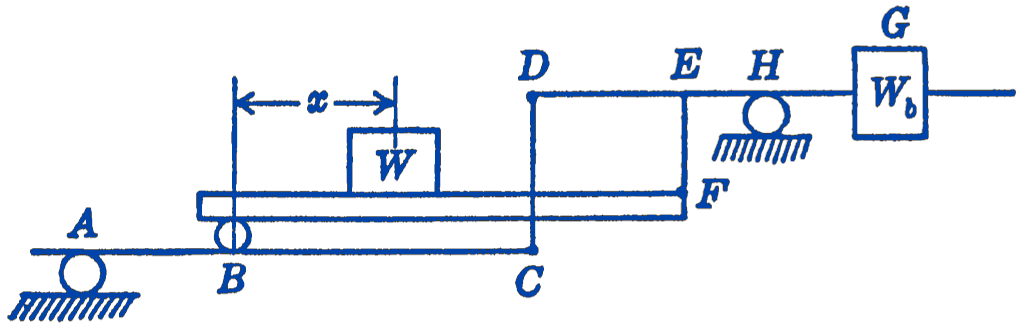
Answer
\(\frac{A B}{A C}=\frac{H E}{H D}\)
4. Two weights are suspended on inextensible cords as shown in the diagram. What is the angle \(\alpha\) for equilibrium?
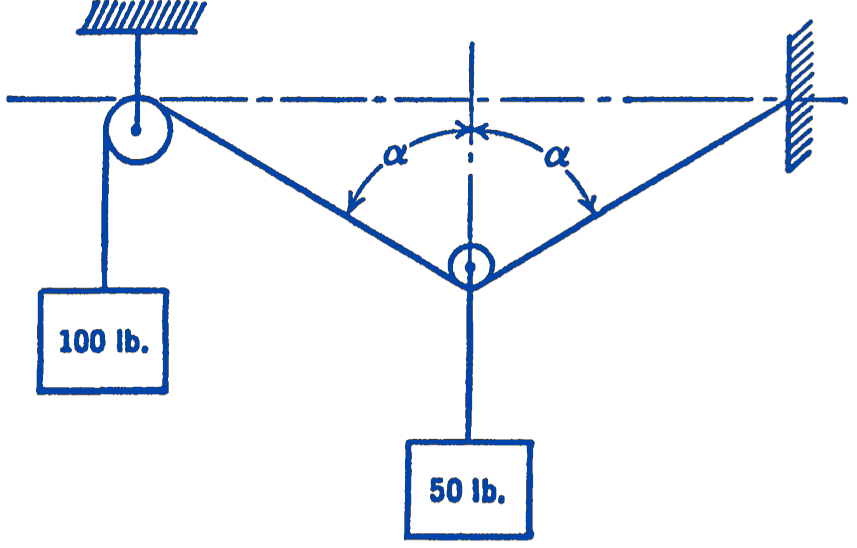
Answer
\(\alpha=\cos ^{-1}\left(\frac{1}{4}\right)\)
5. A uniform bar of weight \(W\) rests on two frictionless inclined planes as shown in the diagram. Show that the position of equilibrium of the bar is such that a virtual displacement would cause the center of gravity of the bar to move horizontally, and find the angle \(\alpha\) for the equilibrium position.
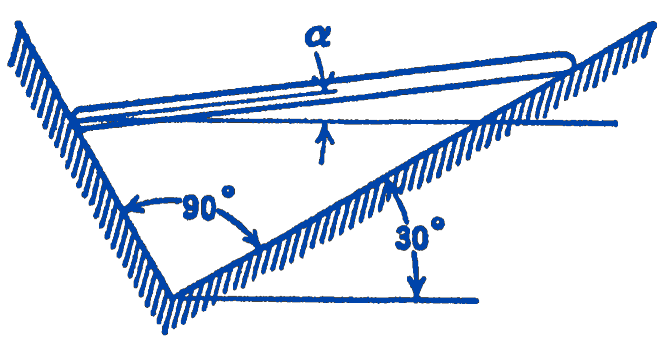
Answer
\(-30^{\circ}\)
6. Find the force \(F\) required to keep the weight \(W\) in equilibrium, by means of the differential pulley arrangement shown in the diagram.
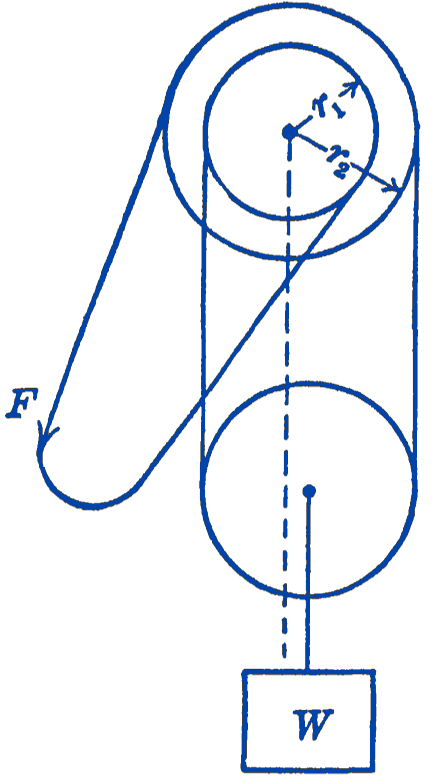
Answer
\(F=W \frac{\left(r_{2}-r_{1}\right)}{2 r_{2}}\)