The principle of virtual displacements can be extended directly to include rigid bodies, which may be thought of as systems of particles. There will be forces between the various particles forming the body, of such a nature that the distances between the particles will remain fixed. These internal forces, however, will always occur in equal and opposite pairs, so that the total work done by them during any motion of the whole body as a rigid body will be equal to zero.

Consider the rigid framework shown in Fig. 1a, supported by a frictionless pin at \(O\), and acted upon by the three external forces \(\mathbf{F}_{1}\), \(\mathbf{F}_{2}\), and \(\mathbf{F}_{3}\), which maintain the system in equilibrium.

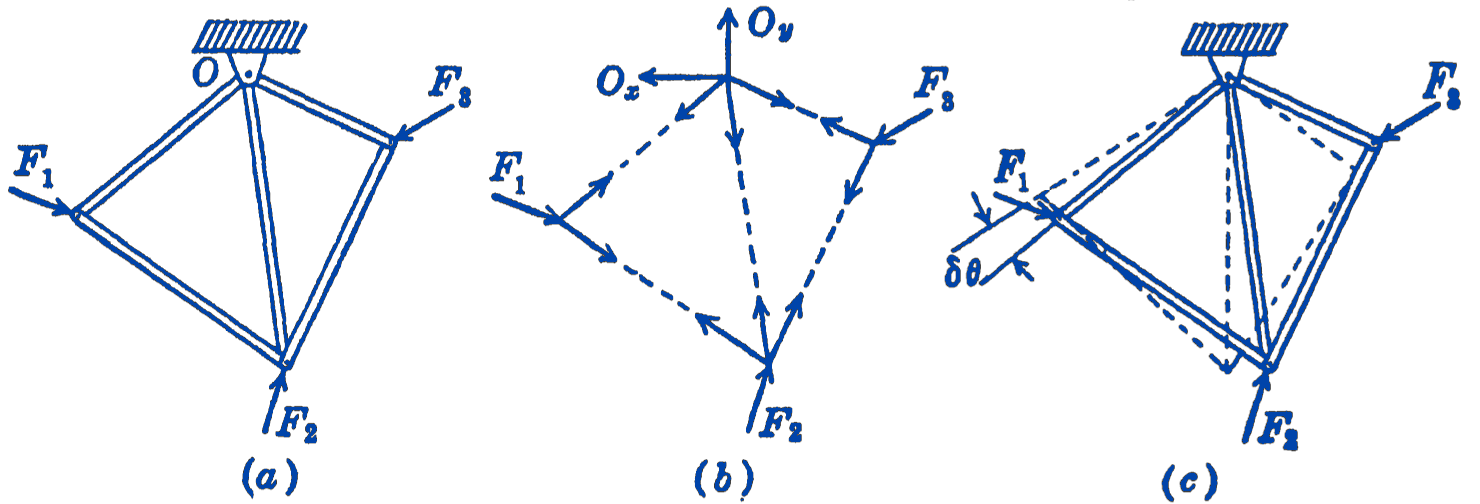
In Fig. 1b, all the forces which are involved in the system are shown. They will be seen to be of three kinds: first, the active external forces \(\mathbf{F}_{1}\), \(\mathbf{F}_{2}\), and \(\mathbf{F}_{3}\); second, the internal forces in the rigid bars, which occur in equal and opposite pairs; and third, the reaction force at the pin \(O\), which is shown as two rectangular components. If now, we imagine the virtual displacement of the system, as shown in Fig. 1c, in which the whole framework has been rotated through some small angle about \(O\), we will see that the forces of the second and third kind will do zero work whether or not the system is in equilibrium, so that for the equilibrium condition we need only consider the first kind of force, and write \[ \sum\left(F_{x} \delta x+F_{y} \delta y+F_{z} \delta z\right)=0 \] where \(F_{x}, F_{y}\), and \(F_{z}\) are the components of the active forces only, and the summation sign indicates that all of such active forces are to be included. We can thus state in general for any system consisting of frictionless constraints and rigid bars that the necessary and sufficient condition for the equilibrium of the system is that the total work done by all of the active forces of the system, upon any arbitrary infinitesimal displacement of the system compatible with the constraints, is equal to zero. This is the most general statement of the principle of virtual displacements.

From the examples given above, and those which will follow, it will be seen that the particular advantage of the principle of virtual displacements is realized in those problems in which one is interested only in the equilibrium relationship between the active forces of the system and is not interested in computing the values of reactions or of internal forces. This does not mean that the principle of virtual displacements can never be used to determine reactions. It is often possible to select the force system to be determined in such a way that the reactive forces can be treated as active forces and can, therefore, be treated by the methods outlined above.

Example 1. A rigid, weightless bar rests against two frictionless walls as shown in Fig. 2. It is held in equilibrium by two forces \(F_{1}\) and \(F_{2}\) parallel to the wall. What is the relationship between \(F_{1}\) and \(F_{2}\) in the position shown?

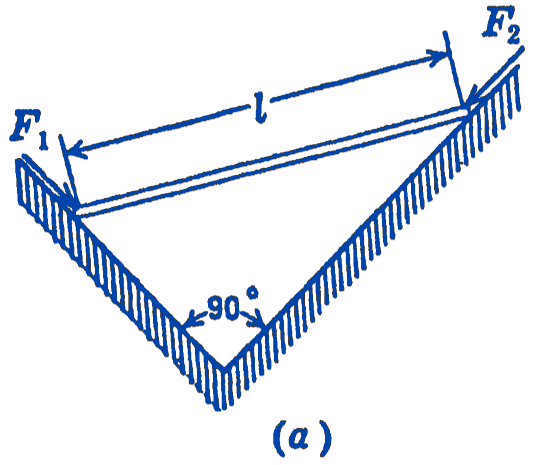
Solution. A displacement of the system compatible with the constraints is shown in Fig 3. From the geometry of the system, we have \(x^{2}+y^{2}=l^{2}\), where \(l\) is a constant; we can find the relationship between \(\delta x\) and \(\delta y\) by differentiating: \[ \begin{aligned} 2 x \delta x+2 y \delta y & =0 \\ \frac{\delta x}{\delta y} & =-\frac{y}{x} \end{aligned} \] From the principle of virtual displacements, we have: \[ \begin{aligned} F_{1} \delta y-F_{2} \delta x & =0 \\ F_{1}=\frac{\delta x}{\delta y} F_{2} & =\frac{y}{x} F_{2} \end{aligned} \] where we omit the negative sign since we have already taken it into account by calling the work done by \(F_{2}\) negative.

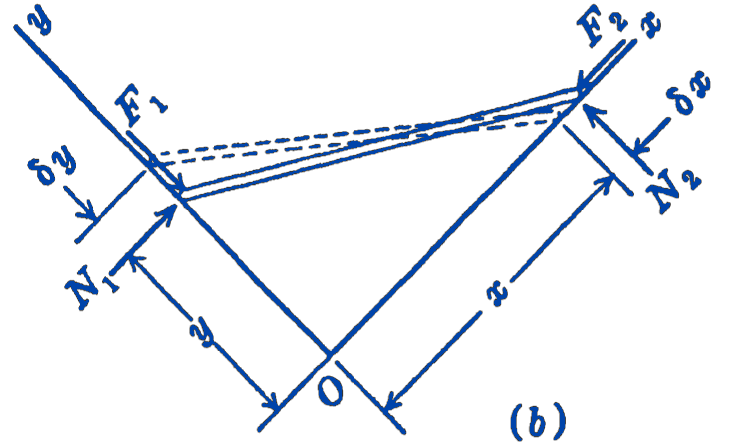
We have thus gone directly to the relationship between \(F_{1}\) and \(F_{2}\) without considering or computing the reactions \(N_{1}\) and \(N_{2}\). If we had solved the problem by our previous equations of equilibrium, we would have included \(N_{1}\) and \(N_{2}\) in the equations and would then have eliminated them algebraically. It should be remembered, however, that in many problems it will be just as important to solve for the reactions as for the active forces.

Example 2. Find the equilibrium relationship between the force \(F_{1}\), derived from the gas pressure in the engine cylinder, and the torque \(M\) about the crankshaft bearing \(O\) (Fig. 4).

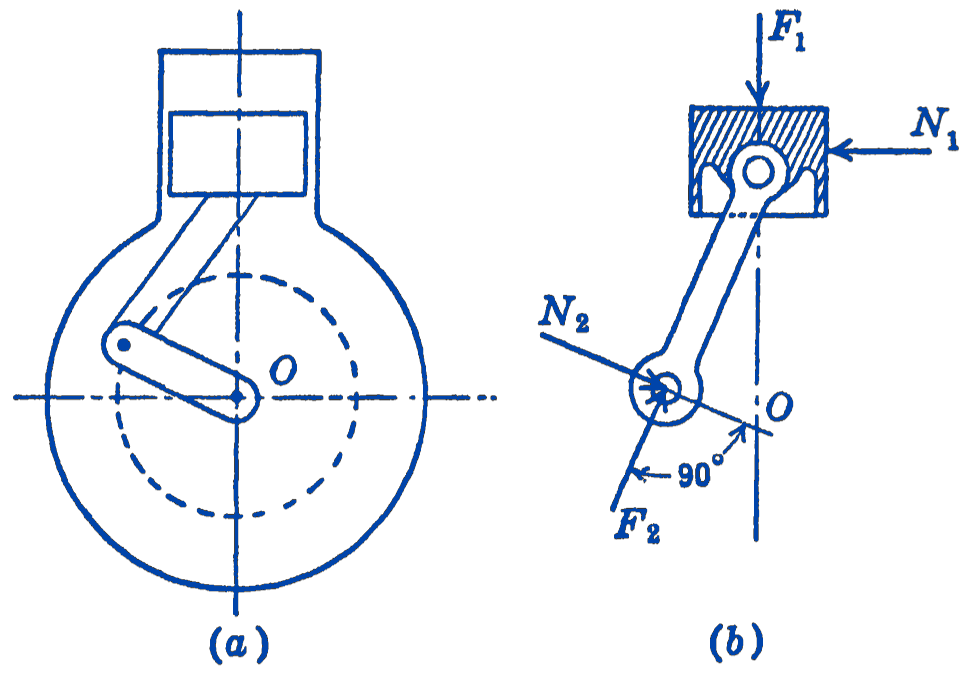
Solution. The active forces in the system are \(F_{1}\), and \(F_{2}\) the force normal to the crank \(O A\). A virtual displacement of the system is shown in (c), which involves a rotation of the crank about \(O\), and a translation of the piston.

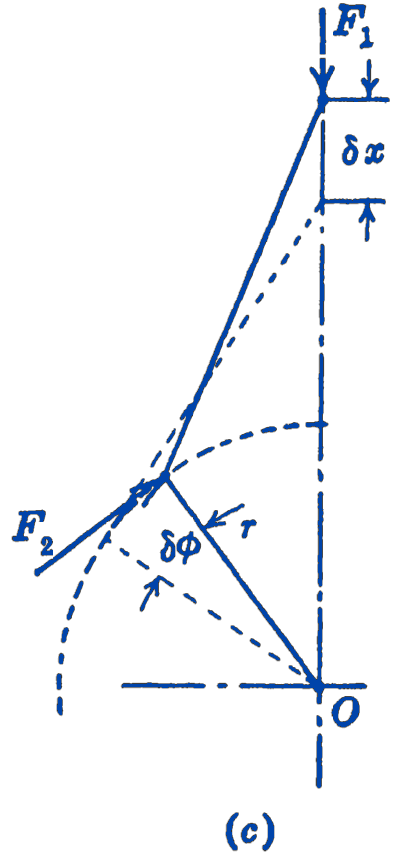
By the principle of virtual displacements we have: \[ \begin{aligned} F_{2}(r) \delta \phi-F_{1} \delta x & =0 \\ F_{2}(r) & =M \end{aligned} \] so that \[ M=F_{1} \frac{\delta x}{\delta \phi} \] If we take the displacements as infinitesimal, we have: \[ M=F_{1} \frac{d x}{d \phi} \] We can find the relationship between \(x\) and \(\phi\) from geometrical considerations in the form: \[ x=f(\phi) \] so that the derivative could be found, and the relationship between \(M\) and \(F_{1}\) would thus be known.

Example 3. A compressive force \(P\) is applied by means of a screw-press as shown in Fig. 5. The screw is turned by a force \(F\) at a distance \(a\) from the axis. The pitch of the screw thread is \(b\), where by pitch we mean the distance which the screw thread would advance, for one complete revolution of the screw. Find the relationship between \(F\) and \(P\).

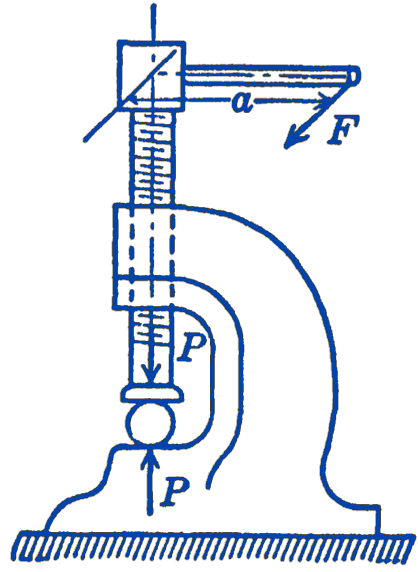
Solution. We take as a virtual displacement of the system a small rotation \(\delta \theta\) of the screw. The screw would then advance a distance \(\frac{b}{2 \pi}(\delta \theta)\). From the principle of virtual displacements we have directly: \[ \begin{aligned} F(a) \delta \theta & =P \frac{b}{2 \pi} \delta \theta \\ P & =\frac{2 \pi a}{b} F \end{aligned} \]

Example 4. A weight \(W\) is to be lifted by means of a force \(F\) applied to the system of two equal pulleys shown in Fig. 6. Find the relationship between \(F\) and \(W\) for equilibrium conditions.

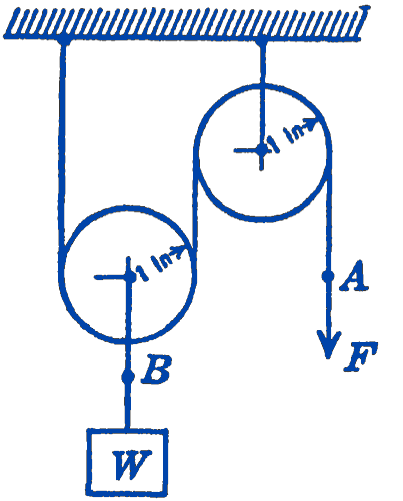
Solution. As the virtual displacement of the system let us take a small vertical motion of the point \(A\) downward, \(\delta y\). Then the point \(B\) will be raised by the amount \(\dfrac{\delta y}{2}\), and the principle of virtual displacements gives: \[ \begin{aligned} F_{1}(\delta y)&-W\left(\frac{\delta y}{2}\right) =0 \\ F &=\frac{W}{2} \end{aligned} \]