As has been shown above in Problem 8 of Section: Conditions of Equilibrium; three non-parallel forces in a plane can be in equilibrium only if they pass through the same point. In some cases where it can be seen that forces act upon a structure at only three points, this fact can be used to introduce a simplification into the solution of the problem. The application of this principle will be seen in the following example.
Example. A semi-circular arch is pinned at the middle and at the ends as shown in Fig. 1a and is loaded on one side by a 1000 lb force as shown. Find the forces at \(A, B\), and \(C\). Neglect the weights of the members.
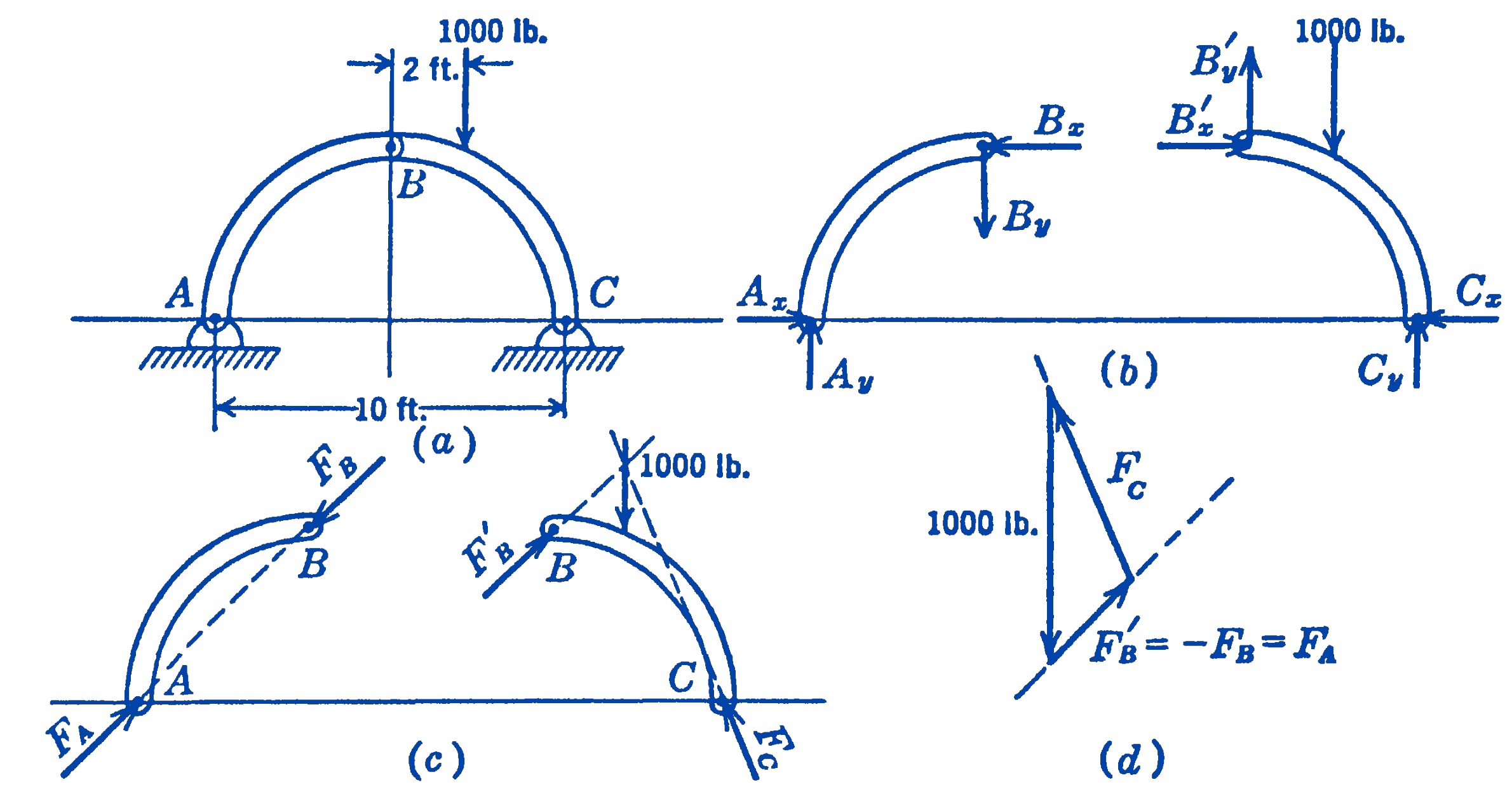
Solution. If the free-body diagram of the two parts of the structure (b) or of the structure as a whole is drawn, we find that there are apparently more unknowns than there are equations. We note, however, in (c), that the left-hand member is a two-force member, and hence the forces at \(A\) and \(B\) must have the direction \(A B\). We also see that the right-hand member is subjected to three forces which must be concurrent. The vector triangle (d) can thus be constructed directly, and the magnitudes of the forces can be determined.