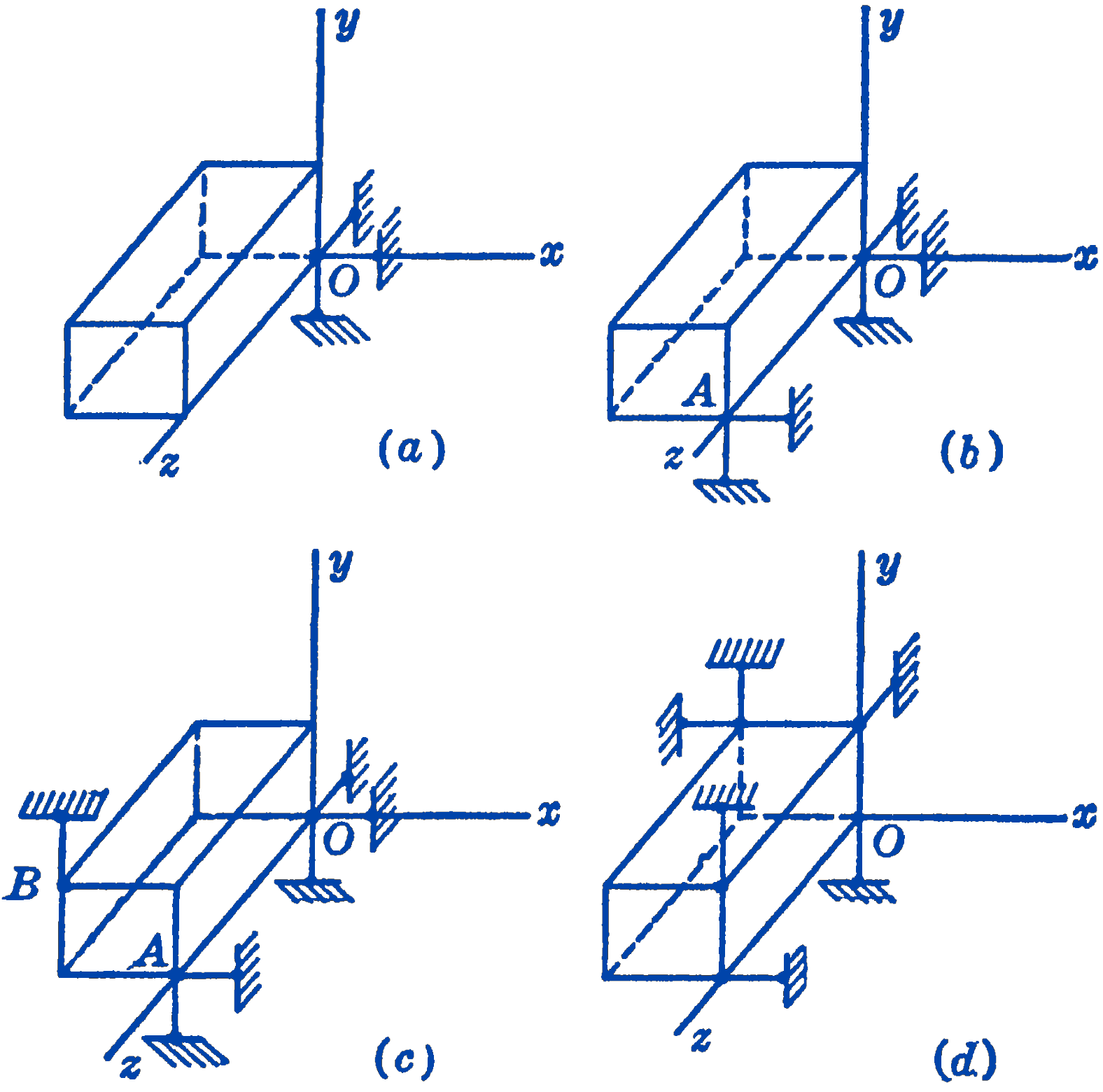
In many problems occurring in the design of instruments and machinery, one does not want to constrain a body completely, but wishes to permit certain types of motion or freedom. By the number of degrees of freedom of a system is meant the number of independent coordinates which would have to be specified in order to fix completely the location of every part of the system. A rigid body which could move only along one straight line, for example, would have one degree of freedom, since one coordinate only, the distance from some arbitrary point to the body, would suffice to fix the position of the body. A body: which could only rotate about an axis would also be a one degree of freedom system, since only the angle of rotation is required to fix the location of all parts of the body. Referring to Fig. 1a of Section: Complete Constraint of a Rigid Body in Space (repeated below) , it will be seen that this system, which is supported by three constraints, has three degrees of freedom, since, for example, three angles about the three coordinate axes would have to be given in order to specify the location of the body. In Fig. 1b the addition of two more constraints reduces the number of degrees of freedom to one, since now only rotation about an axis is possible. It will be found in all cases that the number of degrees of freedom of the system is equal to six minus the number of constraints. This principle is useful in design, since it indicates the number of contacts between the body and its supporting structure which are required for the desired type of motion.¹