We now consider the total number of constraints or supporting elements which are required to constrain completely a rigid body in space.

Consider the body shown in Fig. 1. In Fig. 1a one point of the body, \(O\), has been fixed in space by means of the three rigid hinged bars as shown.

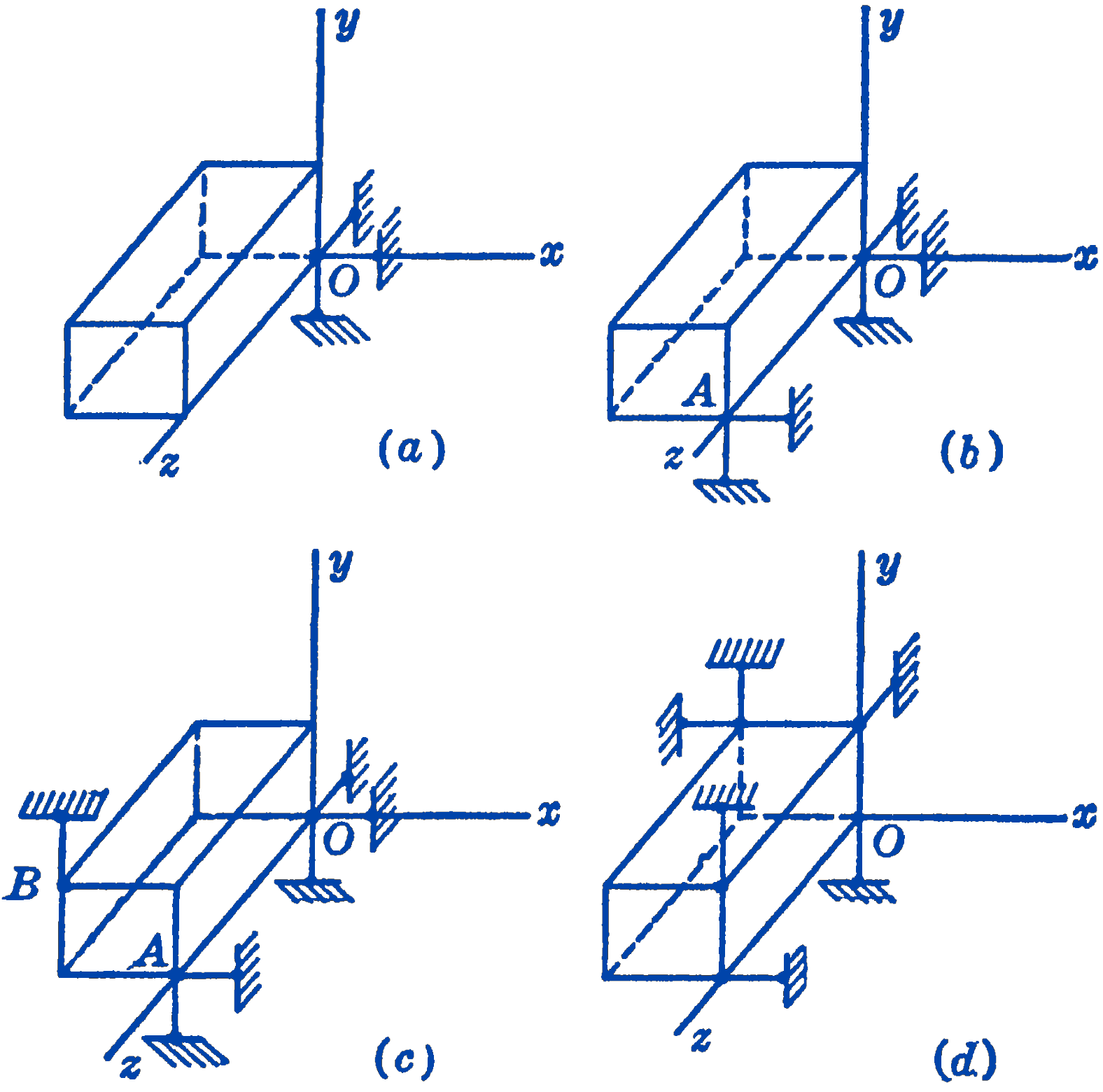
Three non-coplanar bars are required, otherwise motion of the point normal to the plane of the bars can occur. With the constraint shown in Fig. 1a any point in the body is free to move in a spherical surface with \(O\) as a center. In Fig. 1b another point \(A\) has been constrained. This can be done by two bars whose plane is normal to one of the bars at \(O\), as shown. The only possible remaining motion of the body is a rotation about the axis \(O A\), which can be prevented by means of a hinged bar which does not intersect the axis \(O A\). This could be done, for example, by the bar shown at \(B\) in Fig. 1c. It will thus be seen that six elements will constrain completely the body in space. It is not necessary to arrange the elements exactly as shown in Fig. 1c. In Fig. 1d, for example, another arrangement of the six bars is shown which accomplishes the same purpose. It will be found, however, that complete constraint cannot be obtained with less than six elements for the general space system. It will be seen that this is generally true, since for equilibrium, the six components of the known forces (three force components and three couple components) must be balanced by six equal and opposite components of the constraining forces. It is not true, however, that any six elements are sufficient to insure constraint, since the relationships between the supports may be such that motion could occur. If all of the bars, for example, were parallel or were arranged in parallel planes, movement could occur normal to the plane. Similarly, if the axes of the six bars could be intersected by one straight line, there would be a possibility of rotation about that line.

From considerations such as those given above, it can be shown that the necessary and sufficient condition for the complete constraint of a rigid body in space is that it be supported by six hinged bars, or some equivalent structure, whose lines of action cannot be intersected by a straight line. This condition includes the case of the parallel bars, whose lines of action may be said to intersect the same straight line at infinity.

If other bars should be used to support the body, in addition to those required for complete constraint, such additional supports are called redundant constraints. Since six statical equations can be written for the general force system, it will be apparent that the constraining forces for a body loaded in any manner can always be determined from the equations of statics, providing that no redundant constraints exist. This situation, in which there are no redundant constraints, is termed a statically determinate constraint of the body, while the addition of redundant constraints makes the problem statically .

The same conclusions will be found to apply to all of the simpler force systems. In each case the number of supports required for complete constraint is equal to the number of statics equations which can be written for the system.