It can be shown that for any force system the moment of the resultant about any point or axis is equal to the sum of the moments of the individual forces about that point or axis. We shall demonstrate this theorem for the special case of two co-planar, non-parallel forces.
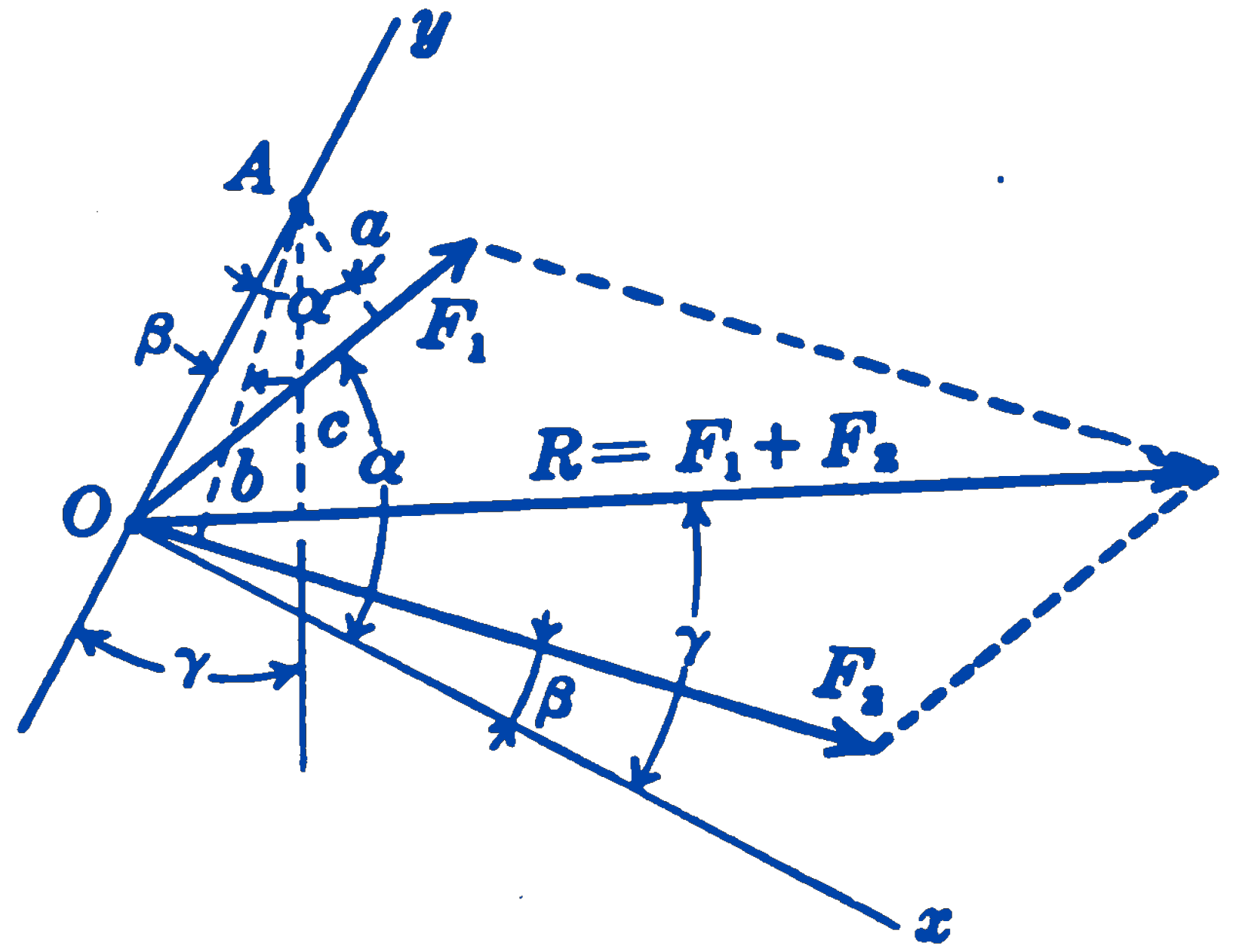
Consider the two forces \(F_1\) and \(F_2\) shown in Fig. 1, with point of concurrence \(O\) and moment-axis \(A\). Take for the \(y\)-axis a line through \(O\) and \(A\). Writing components along the \(x\)-axis, we have: \[ R \cos \gamma = F_1 \cos \alpha + F_2 \cos \beta \] Multiply each term by the distance \(OA\). \[ R(OA) \cos \gamma = F_1(OA) \cos \alpha + F_2(OA) \cos \beta \] From the geometry of Fig. 1, it will be seen that: \[ (OA) \cos \alpha = a \\ (OA) \cos \beta = b \\ (OA) \cos \gamma = c \] so that: \[ R(c) = F_1(a) + F_2(b) \] Since \((F_1)(a)\) is the moment of \(F_1\) about \(A\), \((F_2)(b)\) is the moment of \(F_2\) about \(A\), and \((R)(c)\) the moment of the resultant about \(A\), the theorem for this case is proved.
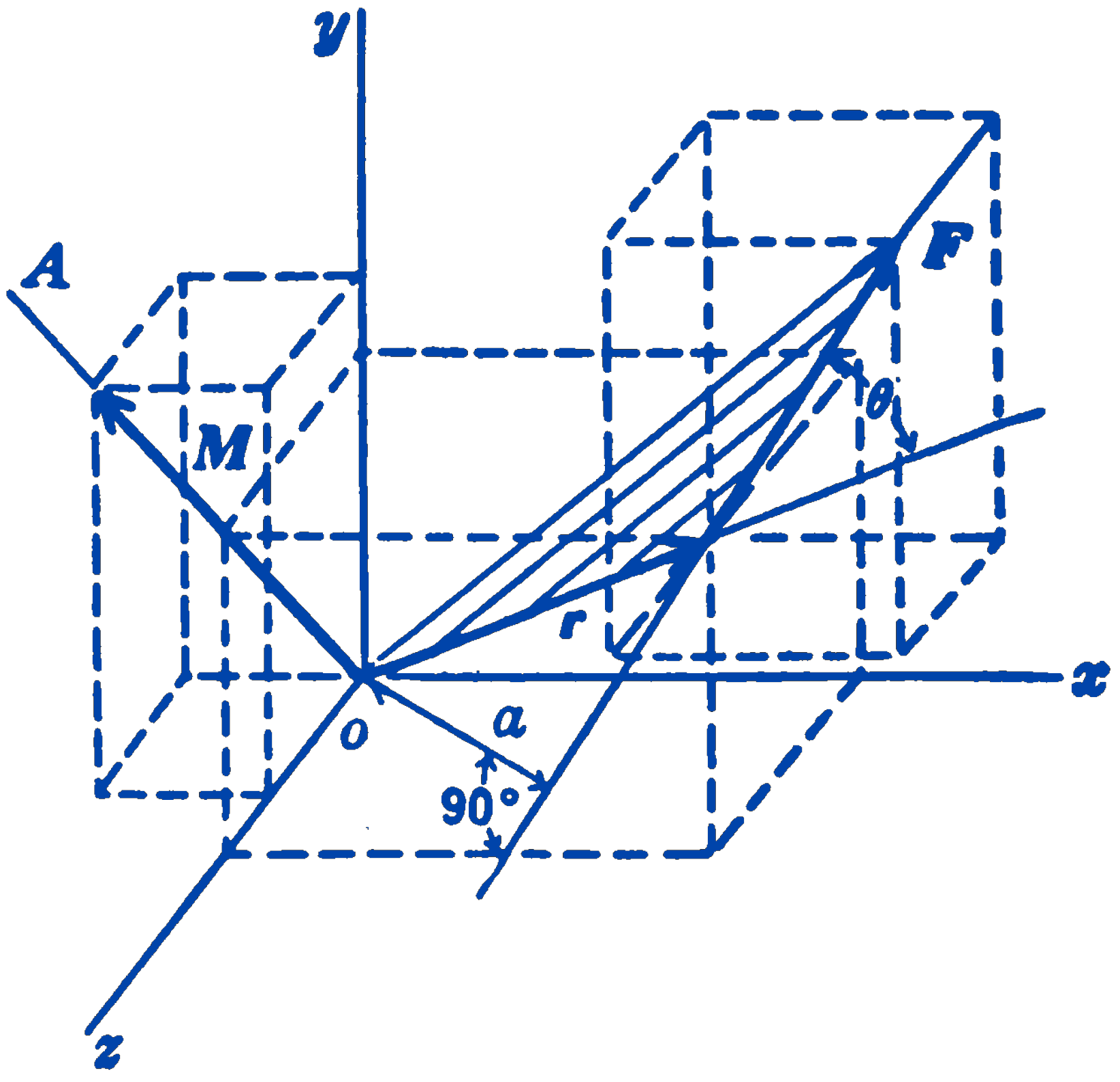
If a moment vector \(M\) is defined with respect to a point \(O\), then its component in any direction \(OD\) is the moment about the line \(OD\). In Fig. 2, using the theorem of moments, the components of \(M\) along the three coordinate axes can be determined by resolving the force \(F\) into its rectangular components \(F_x\), \(F_y\), and \(F_z\) and writing the sums of the moments of these components about the coordinate axes. This gives: \[ \begin{aligned} M_x &= yF_z - zF_y \\ M_y &= zF_x - xF_z \\ M_z &= xF_y - yF_x \end{aligned} \]
The signs of the terms have been fixed by the definition of a moment vector as previously given. If one looks from the origin towards the positive end of the coordinate axes, a clockwise rotation means a positive sign.
1.5.1 PROBLEMS
1. Prove the theorem of moments for a system of two parallel forces. The diagram of Fig. 1 of Section: Systems of Parallel Forces and the results of the accompanying analysis may be used.
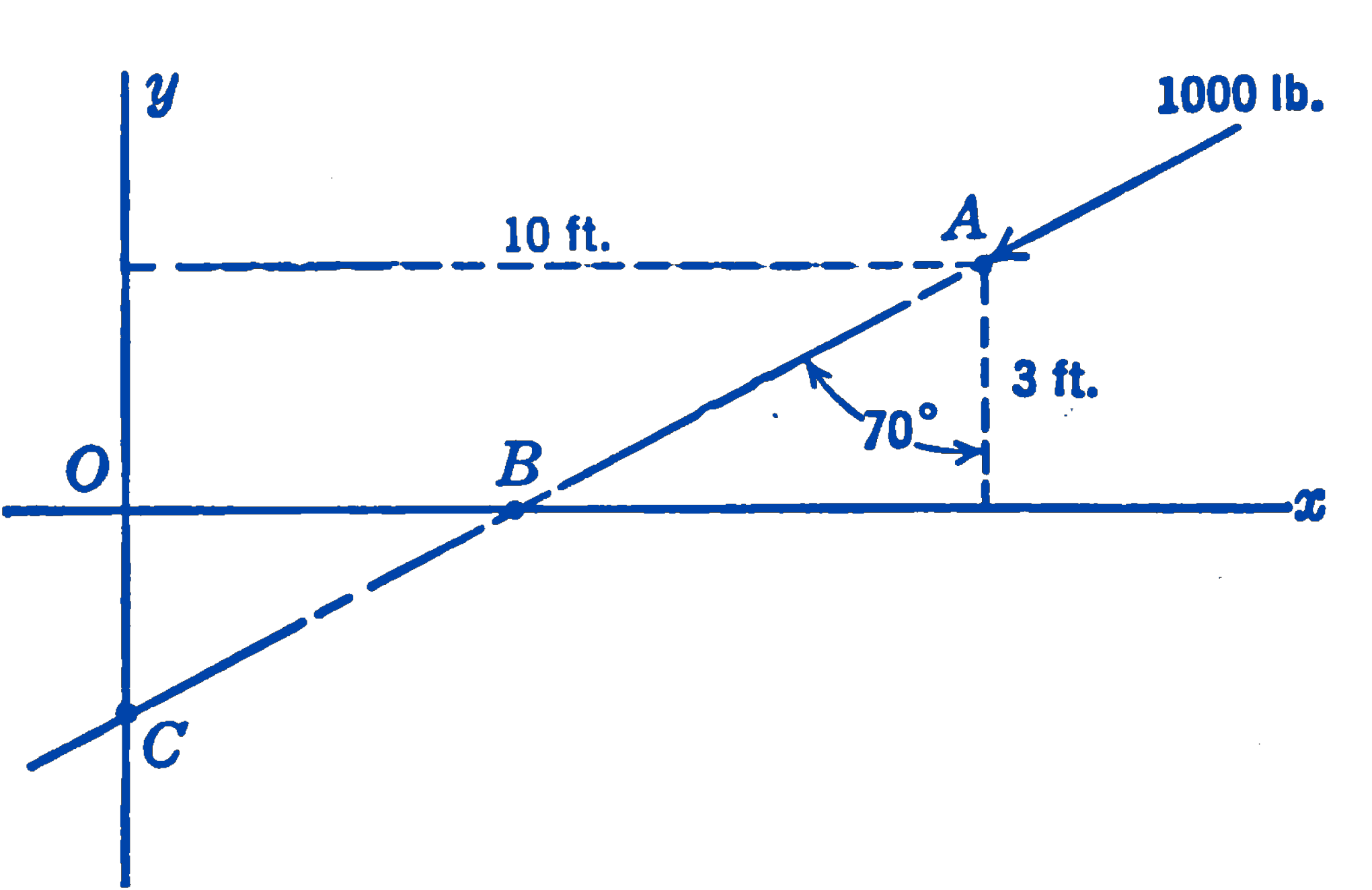
2. Calculate the moment of the 1000-lb force about the point \(O\), (a) by multiplying the force by the perpendicular distance from \(O\) to the line of action of the force, and (b) by resolving the force into rectangular components at the point \(A\), using the theorem of moments. (c) Repeat, by resolving the force into components at points \(B\) and \(C\).
answer
\(-600\ \mathrm{ft}\cdot\mathrm{lb}\)
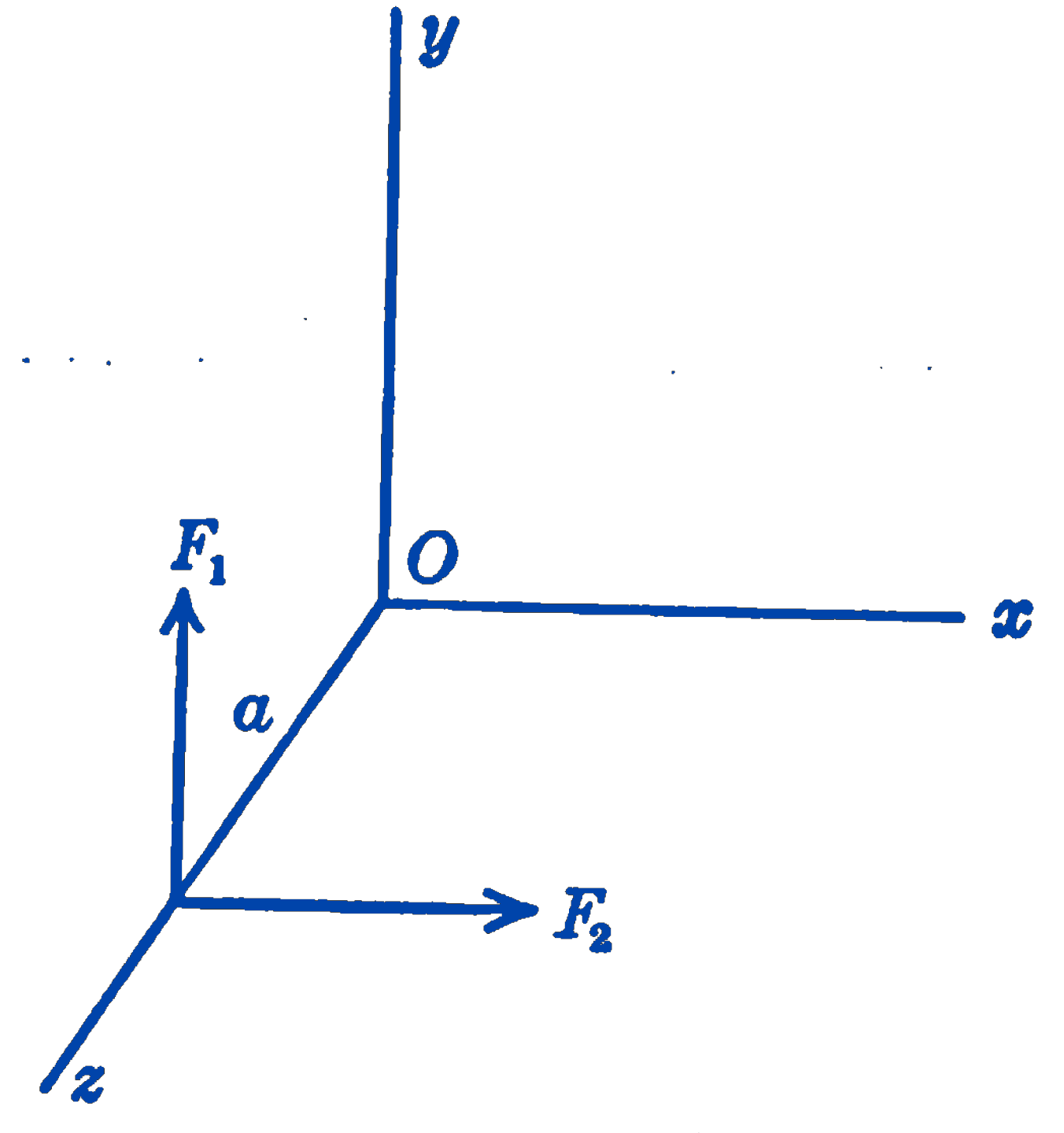
3. \(F_1\) is parallel to the \(y\)-axis and \(F_2\) is parallel to the \(x\)-axis and the lines of action of the two forces intersect the \(z\)-axis at a distance \(a\) from the \(xy\) plane. Show that if the two vectors \(M_1\) and \(M_2\) representing the moments of \(F_1\) and \(F_2\) about \(O\) are added, the resultant vector \(M\) correctly represents the moment of the resultant of the two forces about the point \(O\).
4. Find the moment of the three forces shown in the figure about the axis \(OA\). Do this by first finding the components of the moments along the three coordinate axes, and then by adding the components of these components along the line \(OA\).
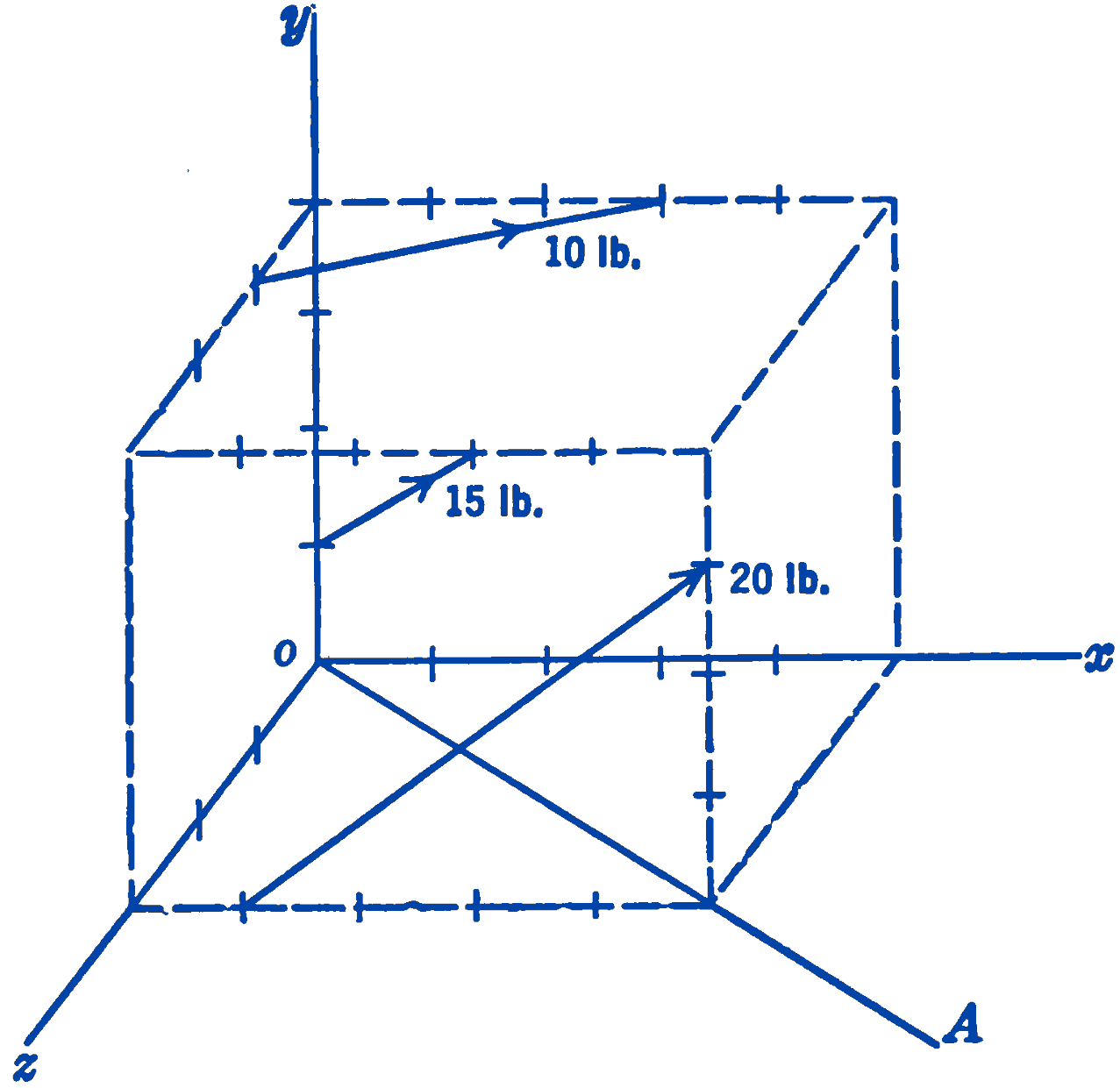
answer
\(-52.1\ \mathrm{ft}\cdot\mathrm{lb}\)
5. Forces \(P, Q,\) and \(R\) are applied along the diagonals as shown in the figure. If \(2P = 2Q = R = 1000\) lb, what is the moment sum about each coordinate axis? What is the resultant moment about \(O\)?
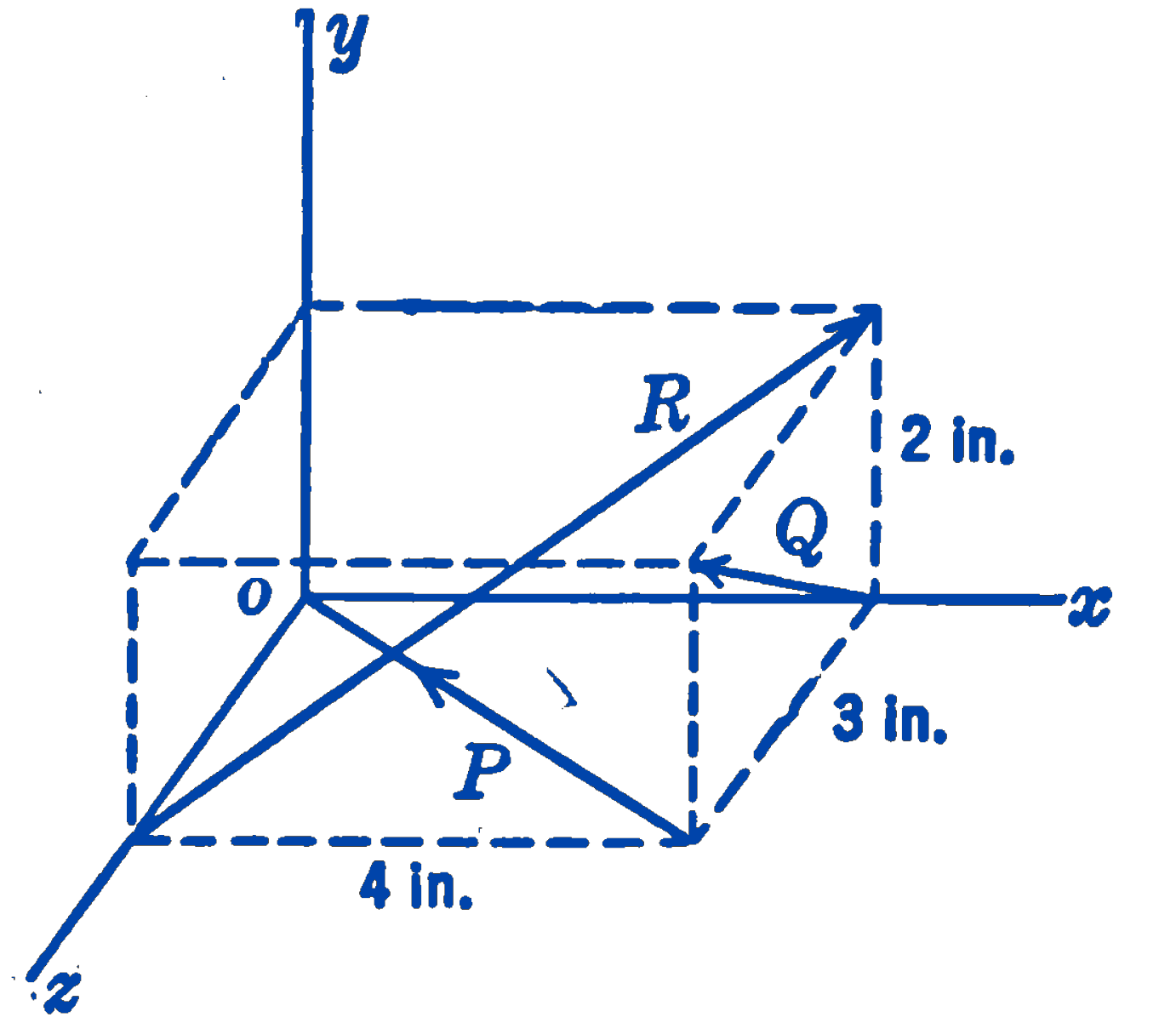
answer
\(M = 1670\ \mathrm{in}\cdot\mathrm{lb}\), \(M_x = -1114\ \mathrm{in}\cdot\mathrm{lb}\); \(M_y = 568\ \mathrm{in}\cdot\mathrm{lb}\), \(M_z = 1108\ \mathrm{in}\cdot\mathrm{lb}\)
6. Given \(F = 600\) lb, \(F_x = M_z = 0\). The point 3, 4, 12 is a point on the line of action of \(F\). Find \(M_y\) and \(M_z\).
answer
\(M_y = -1707\ \mathrm{ft}\cdot\mathrm{lb}\), \(M_z = 570\ \mathrm{ft}\cdot\mathrm{lb}\)
7. A plane force system is found to have: \(\sum F_x = 100\) lb, \(\sum F_y = -160\) lb, \(\Sigma M_0 = 500\ \mathrm{ft}\cdot\mathrm{lb}\). Determine the point at which the resultant force intersects the \(x\)-axis.
answer
\(x = -3.12\)
8. The \(x, y,\) and \(z\) components of a force are \(-20, 50\), and \(25\) lb. The moments are \(M_x = 400\), \(M_y = 180\), \(M_z = -40\ \mathrm{ft}\cdot\mathrm{lb}\). Locate the point of intersection of the force with the \(xz\) plane.
answer
\(x = -0.8\) ft, \(z = -8.0\) ft