The resultant force vector for a system of parallel forces can be found in the usual way by vector addition. The line of action of this resultant, however, cannot be determined by the direct application of the parallelogram law. The method of locating the resultant is shown in Fig. 1 for two parallel forces.

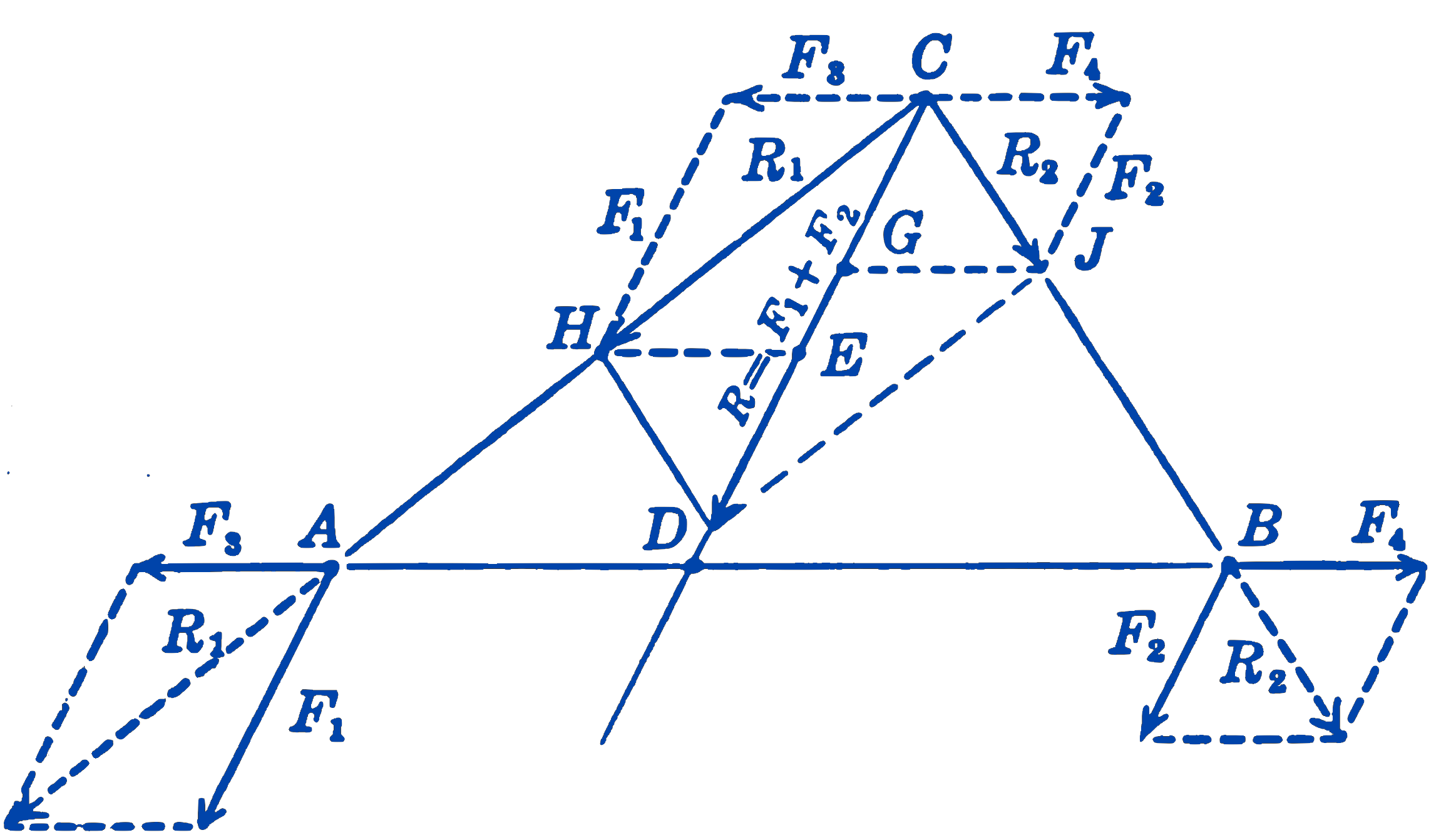
The given forces \(F_1\) and \(F_2\) are applied at the points \(A\) and \(B\) and have parallel lines of action. Suppose that two equal and opposite forces \(F_3\) and \(F_4\) are added to the system in such a way that their common line of action passes through the points \(A\) and \(B\), and that the forces \(F_3\) and \(F_4\) act at the points \(A\) and \(B\) respectively. Since these two forces \(F_3\) and \(F_4\) form a system in equilibrium, their addition will in no way change the conditions of equilibrium of the original system. It is now possible to combine \(F_1\) and \(F_3\), and \(F_2\) and \(F_4\) by means of the parallelogram law, and hence to replace the two original parallel forces \(F_1\) and \(F_2\) by the two non-parallel forces \(R_1\) and \(R_2\). The two forces \(R_1\) and \(R_2\) can then be combined to find the line of action of the resultant of the system.

From Fig. 1, an analytical method of locating the resultant of two parallel forces can be developed. From the geometry of the system we have the following relations: \[ \Delta ACD \text{ is similar to } \Delta CEH \\ \Rightarrow \frac{AD}{CD} = \frac{F_3}{F_1}; \quad (F_3)(CD) = (F_1)(AD) \] \[ \Delta BCD \text{ is similar to } \Delta CGJ \\ \Rightarrow \frac{BD}{CD} = \frac{F_3}{F_2}; \quad (F_3)(CD) = (F_2)(BD) \] thus: \[ (F_1)(AD) = (F_2)(BD) \tag{1} \] \[ \frac{AD}{BD} = \frac{F_2}{F_1} \] This expression gives an analytical method of determining the location of the resultant \(R\).

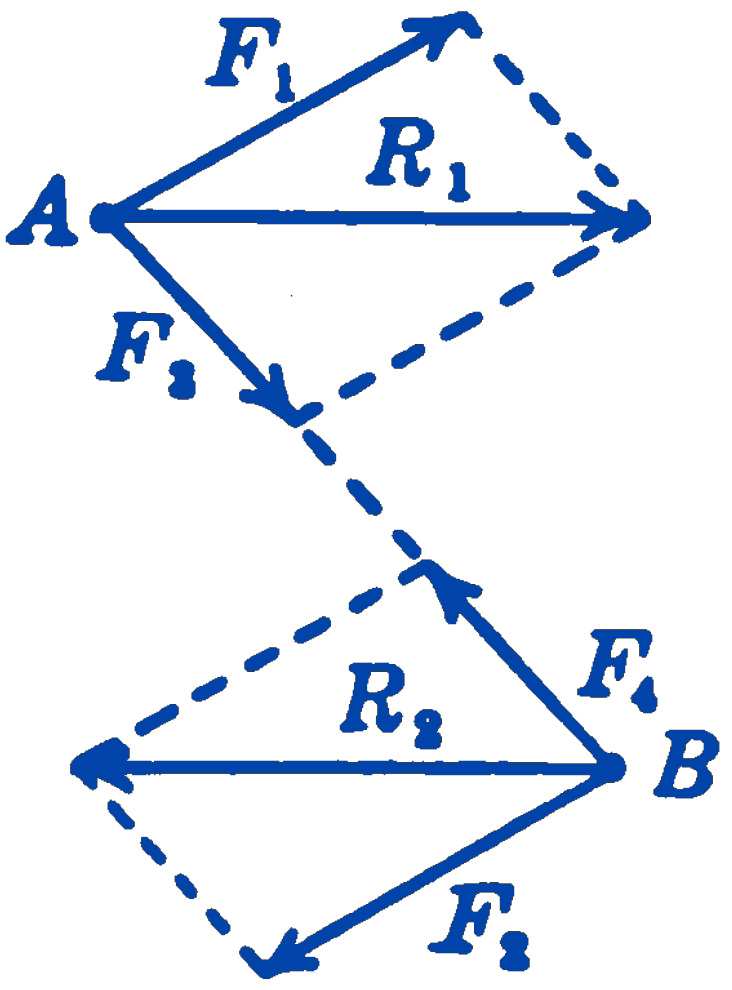
There is one type of parallel force system which has a particularly important property. This is a system of two parallel forces that have equal magnitudes but opposite directions. For this system the vector sum of the two forces vanishes, and there is no single resultant force which is equivalent to the system. It will be seen in Fig. 2 that the graphical method of Fig. 1 also fails to give a solution of a single force for a system of this kind. We thus conclude that a pair of equal, opposite, parallel and non-colinear forces cannot be reduced to a single resultant force, but is already in its simplest form. Such a system of forces is called a couple.

The physical effect of a couple acting on a body is to produce a rotation of the body. Since we need a measure of the tendency of a couple to cause rotation, we are led to the concept of a moment or torque, which is discussed in the following paragraph.