Returning to our consideration of the moment of a force, and referring to Fig. 1 (same as Fig. 1 of Section: The Definition of a Moment), we now see that we can write the moment vector as: \[ \mathbf{M} = \mathbf{r} \times \mathbf{F} \]
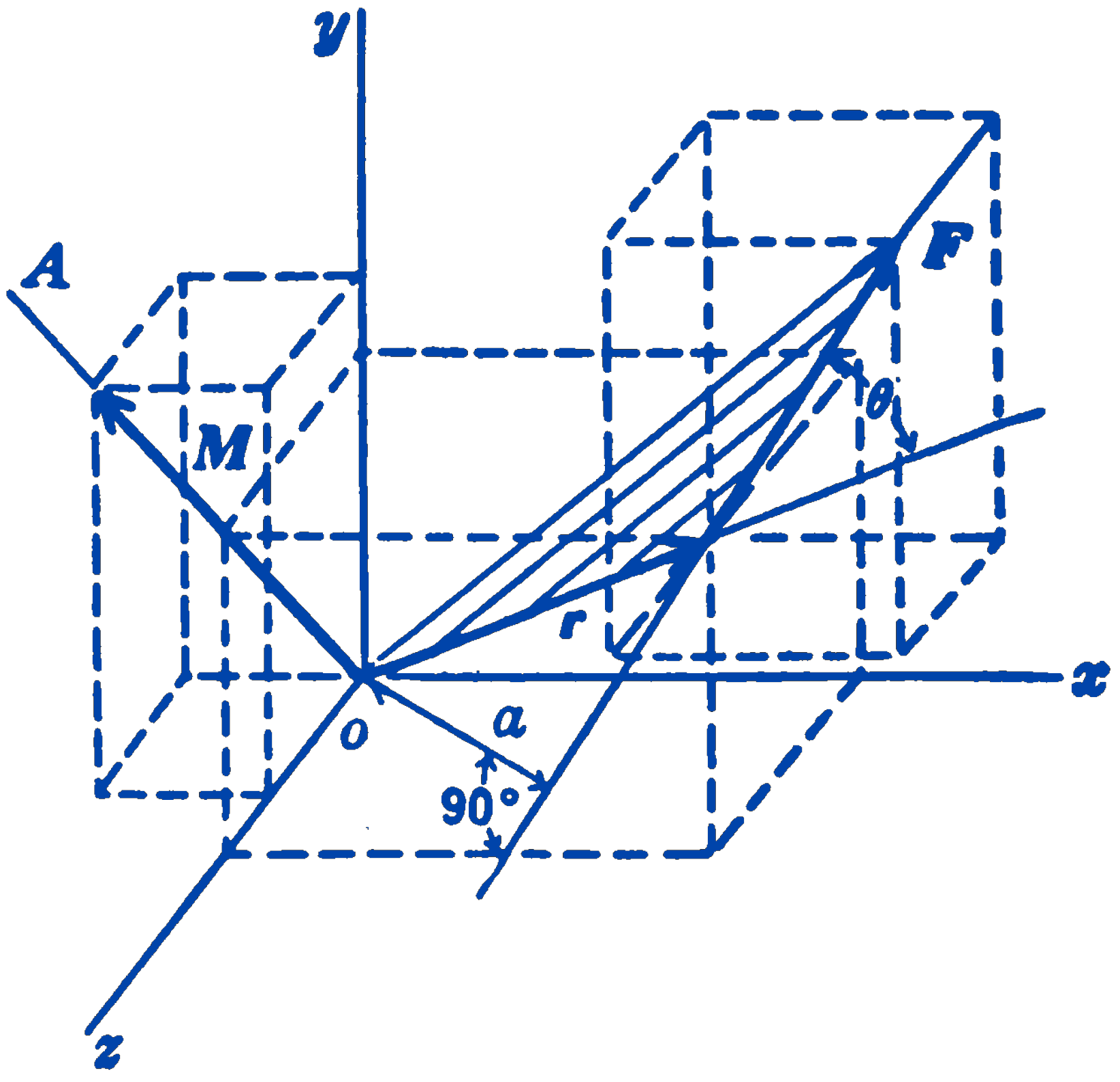
By the definition of the vector product, this statement is equivalent to the definition of a moment given previously. The vector \(\mathbf{r}\) joins the point about which the moment is to be taken and any point on the line of action of the force.
The components of the vector \(\mathbf{M}\) can be written as follows: \[ \mathbf{r} = x \mathbf{i} + y \mathbf{j} + z \mathbf{k} \] \[ \mathbf{F} = F_x \mathbf{i} + F_y \mathbf{j} + F_z \mathbf{k} \] \[ \mathbf{M} = \mathbf{r} \times \mathbf{F} = (yF_z - zF_y) \mathbf{i} + (zF_x - xF_z) \mathbf{j} + (xF_y - yF_x) \mathbf{k} \] so that the components of \(\mathbf{M}\) are: \[ M_x = yF_z - zF_y \] \[ M_y = zF_x - xF_z \] \[ M_z = xF_y - yF_x \]
These are, of course, the same expressions obtained from Fig. 1. The introduction of the vector product makes possible a concise notation for moment vectors. Note that the sign convention for moments previously mentioned is consistent with the sign convention for vector products.
1.10.1 PROBLEMS
1. Show that two vectors \(\mathbf{a}\) and \(\mathbf{b}\) are perpendicular if \(\mathbf{a} \cdot \mathbf{b} = 0\). What is the significance of \(\mathbf{a} \times \mathbf{b} = 0\)?
2. Show that both the scalar product and the vector product obey the distributive law of ordinary multiplication, i.e., \[ (\mathbf{a} + \mathbf{b}) \cdot \mathbf{c} = \mathbf{a} \cdot \mathbf{c} + \mathbf{b} \cdot \mathbf{c} \] \[ (\mathbf{a} + \mathbf{b}) \times \mathbf{c} = \mathbf{a} \times \mathbf{c} + \mathbf{b} \times \mathbf{c} \]
3. Given two vectors \[ \mathbf{a} = 3\mathbf{i} + 2\mathbf{j} + 5\mathbf{k} \] \[ \mathbf{b} = 2\mathbf{i} + \mathbf{j} \]
Find the following vectors: \[ \mathbf{a} + \mathbf{b}; \quad \mathbf{a} - \mathbf{b}; \quad \mathbf{a} \cdot \mathbf{b}; \quad \mathbf{a} \times \mathbf{b} \]
answer
\(\mathbf{a} + \mathbf{b} = 5\mathbf{i} + 3\mathbf{j} + 5\mathbf{k}\)
\(\mathbf{a} - \mathbf{b} = \mathbf{i} + \mathbf{j} + 5\mathbf{k}\)
\(\mathbf{a} \cdot \mathbf{b} = 8\)
\(\mathbf{a} \times \mathbf{b} = -5\mathbf{i} + 10\mathbf{j} - \mathbf{k}\)
4. Show that the vector product can be written as \[ \mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \\ \end{vmatrix} \]
5. Given two vectors \[ \mathbf{a} = 3\mathbf{i} + 2\mathbf{j} + \mathbf{k} \] \[ \mathbf{b} = \mathbf{i} + 3\mathbf{j} + 2\mathbf{k} \] Find the angle between these vectors, using the definition of a scalar product.
answer
38° 11’
6. Find the moment about the point \(\mathbf{i} + 3\mathbf{j} + 2\mathbf{k}\) of a force represented by the vector from the point \(2\mathbf{i} + \mathbf{j} - \mathbf{k}\) to the point \(2\mathbf{i} - \mathbf{k}\) at a scale of 10 lb per ft.
answer
\(-10\mathbf{k} + 30\mathbf{i}\)
7. A body is rotating about an axis with an angular speed of \(\omega\) radians per second. In vector notation \(\boldsymbol{\omega}\) designates the angular velocity with magnitude \(\omega\) and with direction of the axis of rotation given by the right-hand screw rule. If \(\mathbf{v}\) is the linear velocity of a point \(A\) in the above-mentioned body and \(\mathbf{r}\) is the position vector of the point \(A\) with respect to any point of the rotation axis, show that, \[ \mathbf{v} = \boldsymbol{\omega} \times \mathbf{r} \]
8. A body is rotating with an angular speed of 2 radians per second about an axis parallel to \(3\mathbf{j} - 4\mathbf{k}\) passing through the point \(2\mathbf{i} + \mathbf{k}\) ft. Referring to the result of the preceding problem, express vectorially the velocity of the point \(3\mathbf{i} + 2\mathbf{k}\) ft.