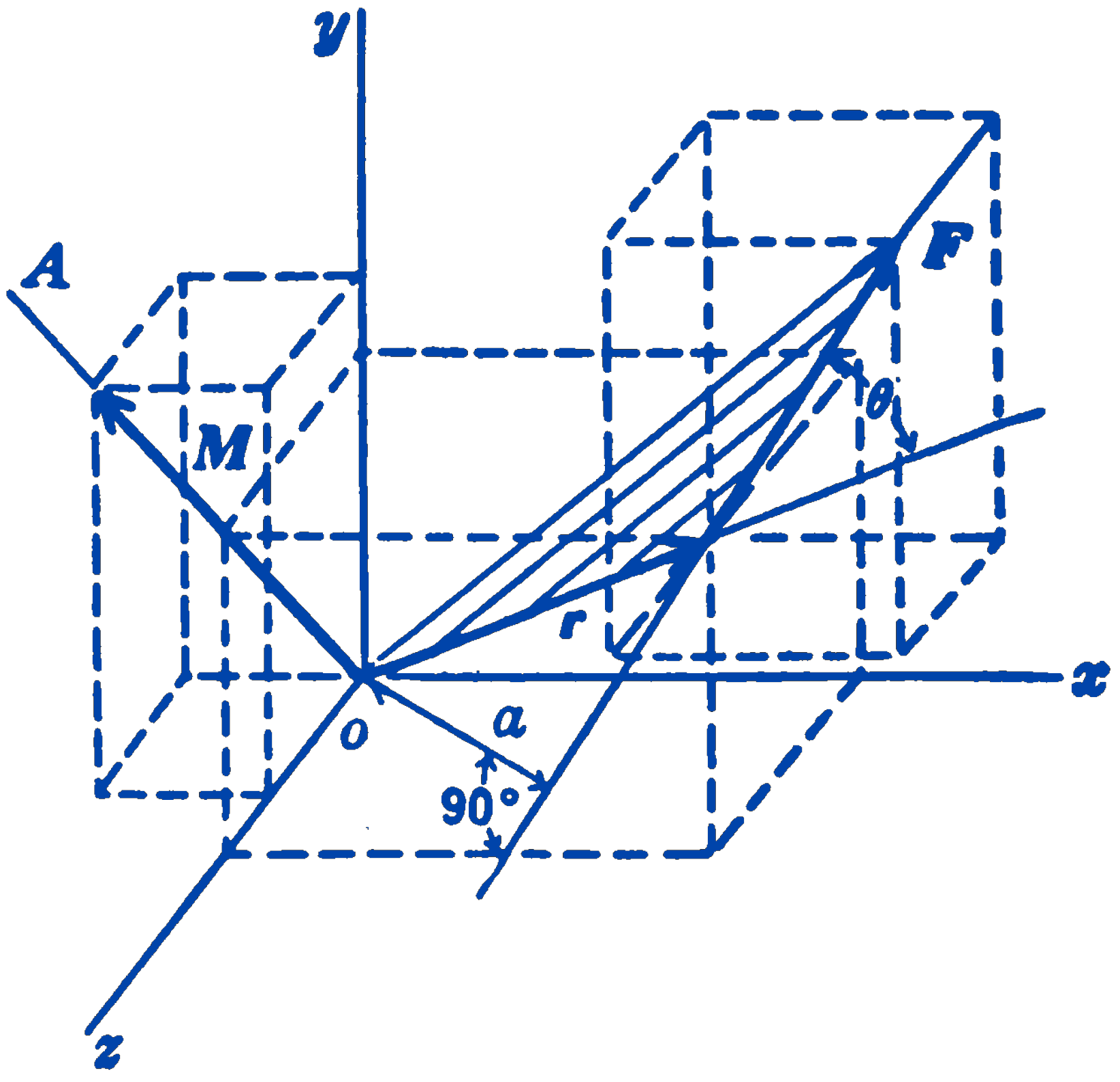
Consider a force \(F\) located a distance \(a\) from the origin \(O\) of a rectangular coordinate system (Fig. 1); \(a\) is measured in the plane of the force \(F\) and the point \(O\), perpendicular to the line of action of \(F\). The moment of \(F\) about the point \(O\), or about the axis through \(O\) normal to the plane of \(F\) and \(O\), is defined as the vector \(M\), whose magnitude is \((F)(a)\), whose direction is the line \(OA\), normal to the plane of \(F\) and \(a\), and whose sense is the direction of advance of a right-handed screw rotated by the force \(F\). This rule for sense may also be stated by saying that if one looks in the direction of \(M\), \(F\) will appear to turn clockwise around \(M\).