The notion of the sample description space of a random phenomenon derives its importance from the fact that it provides a means to define the notion of an event.
Let us first consider what is intuitively meant by an event. Let us consider an urn containing six balls, of which two are white. Let the balls be numbered 1 to 6, the white balls being numbered 1 to 2. Let two balls be drawn from the urn, one after the other; the first ball drawn is not returned to the urn before the second ball is drawn. The sample description space \(S\) of this experiment is given by (3.1) . Now some possible events are (i) the event that the ball drawn on the first draw is white, (ii) the event that the ball drawn on the second draw is white, (iii) the event that both balls drawn are white, (iv) the event that the sum of the numbers on the balls drawn is 7, (v) the event that the sum of the numbers on the balls drawn is less than or equal to 4.
The mathematical formulation that we shall give of the notion of an event depends on the following fact. For each of the events just described there is a set of descriptions such that the event occurs if and only if the observed outcome of the two draws has a description that lies in the set . For example, the event that the ball drawn on the first draw is white can be reformulated as the event that the description of the outcome of the experiment belongs to the set \(\{(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,3)\) , \((2,4),(2,5),(2,6)\}\) . Similarly, events (ii) to (v) described above may be reformulated as the events that the description of the outcome of the experiment belongs to the set (ii) \(\{(2,1),(3,1),(4,1),(5,1),(6,1),(1,2)\) , \((3,2),(4,2),(5,2),(6,2)\}\) , (iii) \(\{(1,2),(2,1)\}\) , (iv) \(\{(1,6),(2,5),(3,4),(4,3)\) , \((5,2),(6,1)\}\) ,(v) \(\{(1,2),(2,1),(1,3),(3,1)\}\) .
Consequently, we define an event as a set of descriptions. To say that an event \(E\) has occurred is to say that the outcome of the random situation under consideration has a description that is a member of \(E\) . Note that there are two notions being defined here, the notion of “an event” and the notion of “the occurrence of an event”. The first notion represents a basic tool for the construction of mathematical models of random phenomena; the second notion is the basis of all translations of statements made in the mathematical model into statements about the real phenomenon.
An alternate way in which the definition of an event may be phrased is in terms of the notion of subset . Consider two sets, \(E\) and \(F\) , of objects of any kind. We say that \(E\) is a subset of \(F\) , denoted \(E \subset F\) , if every member of the set \(E\) is also a member of the set \(F\) . We now define an event as any subset of the sample description space \(S\) . In particular, the sample description space \(S\) is a subset of itself and is thus an event. We call the sample description space \(S\) the certain event, since by the method of construction of \(S\) it will always occur.
It is to be emphasized that in studying a random phenomenon our interest is in the events that can occur (or more precisely, in the probabilities with which they can occur). The sample description space is of interest not for the sake of its members, which are the descriptions, but for the sake of its subsets, which are the events!
We next consider the relations that can exist among events and the operations that can be performed on events. One can perform on events algebraic operations similar to those of addition and multiplication that one can perform on ordinary numbers. The concepts to be presented in the remainder of this section may be called the algebra of events . If one speaks of sets rather than of events, then the concepts of this section constitute what is called set theory .
Given any event \(E\) , it is as natural to ask for the probability that \(E\) will not occur as it is to ask for the probability that \(E\) will occur. Thus, to any event \(E\) , there is an event denoted by \(E^{c}\) and called the complement of \(E\) (or \(E\) complement). The event \(E^{c}\) is the event that \(E\) does not occur and consists of all descriptions in \(S\) which are not in \(E\) .
Let us next consider two events, \(E\) and \(F\) . We may ask whether \(E\) and \(F\) both occurred or whether at least one of them (and possibly both) occurred. Thus we are led to define the events \(E F\) and \(E \cup F\) , called, respectively, the intersection and union of the events \(E\) and \(F\) .
The intersection \(E F\) is defined as consisting of the descriptions that belong to both \(E\) and \(F\) ; consequently, the event \(E F\) is said to occur if and only if both \(E\) and \(F\) occur, which is to say that the observed outcome has a description that is a member of both \(E\) and \(F\) .
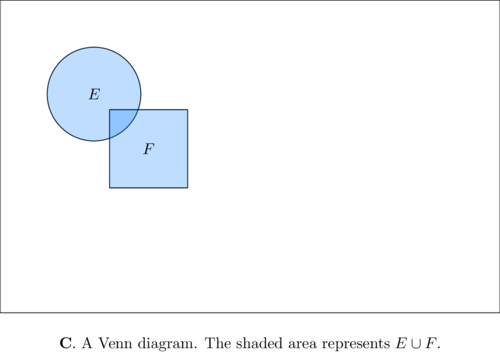
The union \(E \cup F\) is defined as consisting of the descriptions that belong to at least one of the events \(E\) and \(F\) ; consequently, the event \(E \cup F\) is said to occur if and only if either \(E\) or \(F\) occurs, which is to say that the observed outcome has a description that is a member of either \(E\) or \(F\) (or of both).
It should be noted that many writers denote the intersection of two events by \(E \cap F\) rather than by \(E F\) .
We may give a symbolic representation of these operations in a diagram called a Venn diagram (Figs. 4A to 4C ). Let the sample description space \(S\) be represented by the interior of a rectangle in the plane; let the event \(E\) be represented by the interior of a circle that lies within the rectangle; and let the event \(F\) be represented by the interior of a square also lying within the rectangle (but not necessarily overlapping the circle, although in Fig. 4B it is drawn that way). Then \(E^{c}\) , the complement of \(E\) , is represented in Fig. 4A by the points within the rectangle outside the circle; \(E F\) , the intersection of \(E\) and \(F\) , is represented in Fig. 4B by the points within the circle and the square; \(E \cup F\) , the union of \(E\) and \(F\) , is represented in Fig. 4C by the points lying within the circle or the square.


As another illustration of the notions of the complement, union, and intersection of events, let us consider the experiment of drawing a ball from an urn containing twelve balls, numbered 1 to 12. Then \(S=\) \(\{1,2, \ldots, 12\}\) . Consider events \(E=\{1,2,3,4,5,6\}\) and \(F=\{4,5,6,7,8,9\}\) . Then \(E^{c}=\{7,8,9,10,11,12\}, \quad E F=\{4,5,6\} \quad\) and \(\quad E \cup F=\) \(\{1,2,3,4,5,6,7,8,9\}\) .
One of the main problems of the calculus of events is to establish the equality of two events defined in two different ways. Two events \(E\) and \(F\) are said to be equal , written \(E=F\) , if every description in one event belongs to the other. The definition of equality of two events may also be phrased in terms of the notion of subevent . An event \(E\) is said to be a sub-event of an event \(F\) , written \(E \subset F\) , if the occurrence of \(E\) necessarily implies the occurrence of \(F\) . In order for this to be true, every description in \(E\) must belong also to \(F\) , so \(E\) is a sub-event of \(F\) if and only if \(E\) is a subset of \(F\) .
We then have the basic principle that \(E\) equals \(F\) if and only if \(E\) is a sub-event of \(F\) and \(F\) is a sub-event of \(E\) . In symbols,
\[E=F \quad \text { if and only if }\qquad E \subset F \quad \text { and } \quad F \subset E. \tag{4.1}\]
The interesting question arises whether the operations of event union and event intersection may be applied to an arbitrary pair of events \(E\) and \(F\) . In particular, consider two events, \(E\) and \(F\) , that contain no descriptions in common; for example, suppose \(S=\{1,2,3,4,5,6\}, E=\{1,2\}, F=\) \(\{3,4\}\) . The union \(E \cup F=\{1,2,3,4\}\) is defined. However, what meaning is to be assigned to the intersection \(E F\) ? To meet this need, we introduce the notion of the impossible event , denoted by \(\emptyset\) . The impossible event \(\emptyset\) is defined as the event that contains no descriptions and therefore cannot occur . In set theory the impossible event is called the empty set. One important property of the impossible event is that it is the complement of the certain event \(S\) ; clearly \(S^{c}=\emptyset\) , for it is impossible for \(S\) not to occur. A second important property of the impossible event is that it is equal to the intersection of any event \(E\) and its complement \(E^{c}\) ; clearly, \(E E^{c}=\emptyset\) , for it is impossible for both an event and its complement to occur simultaneously.
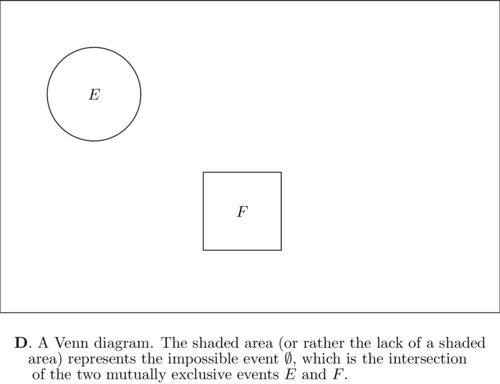
Any two events, \(E\) and \(F\) , that cannot occur simultaneously, so that their intersection \(E F\) is the impossible event, are said to be mutually exclusive (or disjoint). Thus, two events, \(E\) and \(F\) , are mutually exclusive if and only if \(E F=\emptyset\) .
Two mutually exclusive events may be represented on a Venn diagram by the interiors of two geometrical figures that do not overlap, as in Fig. 4D . The impossible event may be represented by the shaded area on a Venn diagram, in which there is no shading, as in Fig. 4D .
Events may be defined verbally, and it is important to be able to express them in terms of the event operations. For example, let us consider two events, \(E\) and \(F\) . The event that exactly one of the events, \(E\) and \(F\) , will occur is equal to \(E F^{c} \cup E^{c} F\) ; the event that exactly none of the events, \(E\) and \(F\) , will occur is equal to \(E^{c} F^{c}\) . The event that at least one (that is, one or more) of the events, \(E\) or \(F\) , will occur is equal to \(E \cup F\) . The event that at most one (that is, one or less) of the events will occur is equal to \((E F)^{c}=\) \(E^{c} \cup F^{c}\) .
The operations of event union and event intersection have many of the algebraic properties of ordinary addition and multiplication of numbers (although they are conceptually quite distinct from the latter operations). Among the important algebraic properties of the operations \(E \cup F\) and \(E F\) are the following relations, which hold for any events \(E, F\) , and \(G\) :
\[\begin{array}{lll} \text { Commutative law } & E \cup F=F \cup E & E F=F E \\ \text { Associative law } & E \cup(F \cup G)=(E \cup F) \cup G & E(F G)=(E F) G \\ \text { Distributive law } & E(F \cup G)=E F \cup E G & E \cup(F G)=(E \cup F)(E \cup G) \\ \text { Idempotency law } & E \cup E=E & E E=E \end{array}\]
Because the operations of union and intersection are commutative and associative, there is no difficulty in defining the union and intersection of an arbitrary number of events, \(E_{1}, E_{2}, \ldots, E_{n}, \ldots\) . The union, written \(E_{1} \cup E_{2} \cup \ldots E_{n} \cup \ldots\) , is defined as the event consisting of all descriptions that belong to at least one of the events . The intersection, written \(E_{1} E_{2} \ldots E_{n} \ldots\) , is defined as the event consisting of all descriptions that belong to all the events.
An unusual property of the event operations, which is used very frequently, is given by de Morgan’s laws , which state, for any two events, \(E\) and \(F\) ,
\[(E \cup F)^{c}=E^{c} F^{c}, \quad(E F)^{c}=E^{c} \cup F^{c}, \tag{4.2}\]
and for \(n\) events, \(E_{1}, E_{2}, \ldots, E_{n}\) ,
\begin{align} \left(E_{1} \cup E_{2} \cup \cdots \cup E_{n}\right)^{c} & =E_{1}^{c} E_{2}^{c} \cdots E_{n}^{c}, \tag{4.3} \\ \left(E_{1} E_{2} \cdots E_{n}\right)^{c} & =E_{1}^{c} \cup E_{2}^{c} \cup \cdots \cup E_{n}^{c} . \end{align}
An intuitive justification for (4.2) and (4.3) may be obtained by considering Venn diagrams.
In section 5 we require the following formulas for the equality of certain events. Let \(E\) and \(F\) be two events defined on the same sample description space \(S\) . Then
\[E \emptyset=\emptyset, \quad E \cup \emptyset=E . \tag{4.4}\]
\[F=F E \cup F E^{c}, \quad E \cup F=F \cup E F^{c}=E \cup F E^{c}. \tag{4.5}\] \[F \subset E \quad \text { implies } E F=F \qquad E \cup F=E. \tag{4.6}\]
In order to verify these identities, one can establish in each case that the left-hand side of the identity is a subevent of the right-hand side and that the right-hand side is a subevent of the left-hand side.
Exercises
4.1. An experiment consists of drawing 3 radio tubes from a lot and testing them for some characteristic of interest. If a tube is defective, assign the letter \(D\) to it. If a tube is good, assign the letter \(G\) to it. A drawing is then described by a 3-tuple, each of whose components is either \(D\) or \(G\) . For example, \((D, G, G)\) denotes the outcome that the first tube drawn was defective and the remaining 2 were good. Let \(A_{1}\) denote the event that the first tube drawn was defective, \(A_{2}\) denote the event that the second tube drawn was defective, and \(A_{3}\) denote the event that the third tube drawn was defective. Write down the sample description space of the experiment and list all sample descriptions in the events \(A_{1}, A_{2}, A_{3}, A_{1} \cup A_{2}, A_{1} \cup A_{3}, A_{2} \cup A_{3}\) , \(A_{1} \cup A_{2} \cup A_{3}, A_{1} A_{2}, A_{1} A_{3}, A_{2} A_{3}, A_{1} A_{2} A_{3}\) .
Answer
\begin{align} &S=\{(D, D, D),(D, D, G),(D, G, D),(D, G, G),(G, D, D),(G, D, G), (G, G, D),(G, G, G)\}, \\ &A_{1}=\{(D, D, D),(D, D, G),(D, G, D),(D, G, G)\}, \\ &A_{1} A_{2} =\{(D, D, D),(D, D, G)\}, \\ &A_{1} \cup A_{2}=\{(D, D, D),(D, D, G),(D, G, D), (D, G, G),(G, D, D),(G, D, G)\}. \end{align}
4.2. For each of the following 16 events draw a Venn diagram similar to Figure \(4 A\) or \(4 B\) and on it shade the area corresponding to the event. Only 7 diagrams will be required to illustrate the 16 events, since some of the events described are equivalent.(i) \(A B^{c}\) , (ii) \(A B^{c} \cup A^{c} B\) , (iii) \((A \cup B)^{c}\) , (iv) \(A^{c} B^{c}\) , (v) \((A B)^{c}\) , (vi) \(A^{c} \cup B^{c}\) , (vii) the event that exactly 0 of the events, \(A\) and \(B\) , occurs, (viii) the event that exactly 1 of the events, \(A\) and \(B\) , occurs, (ix) the event that exactly 2 of the events, \(A\) and \(B\) , occur, (x) the event that at least 0 of the events \(A\) and \(B\) , occurs, (xi) the event that at least 1 of the events, \(A\) and \(B\) , occurs, (xii) the event that at least 2 of the events, \(A\) and \(B\) , occur, (xiii) the event that no more than 0 of the events, \(A\) and \(B\) , occurs, (xiv) the event that no more than 1 of the events, \(A\) and \(B\) , occurs, (xv) the event that no more than 2 of the events, \(A\) and \(B\) , occur, (xvi) the event that \(A\) occurs and \(B\) does not occur. Remark: By “at least 1” we mean “1 or more”, by “no more than 1” we mean “1 or less”, and so on.
4.3. Let \(S=\{1,2,3,4,5,6,7,8,9,10,11,12\}\) , \(A=\{1,2,3,4,5,6\}\) , and \(B=\{4,5,6,7,8,9\}\) . For each of the events described in exercise 4.2, write out the numbers that are members of the event.
Answer
(i), (xvi) \(\{1,2,3\}\) ; (ii), (viii) \(\{1,2,3,7,8,9\}\) ; (iii), (iv), (vii), (xiii) \(\{10,11,12\}\) ;
(v), (vi), (xiv) \(\{1,2,3,7,8,9,10,11,12\}\) ; (ix), (xii), \(\{4,5,6\}\) ; (xi) \(\{1,2,3,4,5,6\) , \(7,8,9\}\) ; (x), (xv) \(S\) .
4.4. For each of the following 12 events draw a Venn diagram and on it shade the area corresponding to the event: the event that of the events \(A, B, C\) , there occur (i) exactly 0, (ii) exactly 1, (iii) exactly 2, (iv) exactly 3, (v) at least 0, (vi) at least 1, (vii) at least 2, (viii) at least 3, (ix) no more than 0, (x) no more than 1, (xi) no more than 2, (xii) no more than 3.
4.5. Let \(S, A, B\) be as in exercise 4.3, and let \(C=\{7,8,9\}\) . For each of the events described in exercise 4.4, write out the numbers that are members of the event.
Answer
(i) \(\{10,11,12\}\) ; (ii) \(\{1,2,3\}\) ; (iii) \(\{4,5,6,7,8,9\}\) ; (iv) \(\phi\) ; (v) \(S\) ;
(vi) \(\{1,2,3,4,5,6,7,8,9\}\) ; (vii) \(\{4,5,6,7,8,9\}\) ; (viii) \(\phi\) ; (ix) \(\{10,11,12\}\) ;
(x) \(\{1,2,3,10,11,12\}\) ; (xi) \(S\) ; (xii) \(S\) .
4.6. Prove (4.4) . Note that (4.4) states that the impossible event behaves under the operations of intersection and union in a manner similar to the way in which the number 0 behaves under the operations of multiplication and addition.
4.7. Prove (4.5) . Show further that the events \(F\) and \(E F^{c}\) are mutually exclusive.