The notion of the uniform probability law (or uniform distribution) over the interval \(a\) to \(b\) , in which \(a\) and \(b\) are finite real numbers, is best defined in the following manner. Consider a numerical valued random phenomenon whose values can lie only in a certain finite interval \(S\) ; that is \(S=\{\) real numbers \(x: a \leq x \leq b\}\) for some finite numbers \(a\) and \(b\) . The random phenomenon is said to obey a uniform probability law over the finite interval \(S\) if the value \(P[B]\) of its probability function, at any interval \(B\) , satisfies the relation
\begin{align} P[B] = \begin{cases} \frac{\text{length of } B}{\text{length of } S}, & \text{if } B \text{ is a subset of } S \\[2mm] 0, & \text{if } B \text{ and } S \text{ have no points in common.} \end{cases} \tag{5.1} \end{align}
It should be noted that knowing \(P[B]\) at intervals suffices to determine it on any Borel set \(B\) of real numbers.
From (5.1) one sees that the notion of a uniform distribution represents an extension of the notion of a finite sample description space \(S\) with equally likely descriptions , since in this case the probability \(P[A]\) of any event \(A\) on \(S\) is given by the formula
\[P[A]=\frac{\text { size of } A}{\text { size of } S}. \tag{5.2}\]
There are many random phenomena for which it appears plausible to assume a uniform probability law. For example, suppose one is tossing a dart at a line marked 0 to 1. If one is always sure to land on the line and if one feels that , then one is led to conclude that the place at which the dart hits the line has a probability function satisfying (5.1) , with \(S\) denoting the interval 0 to 1.
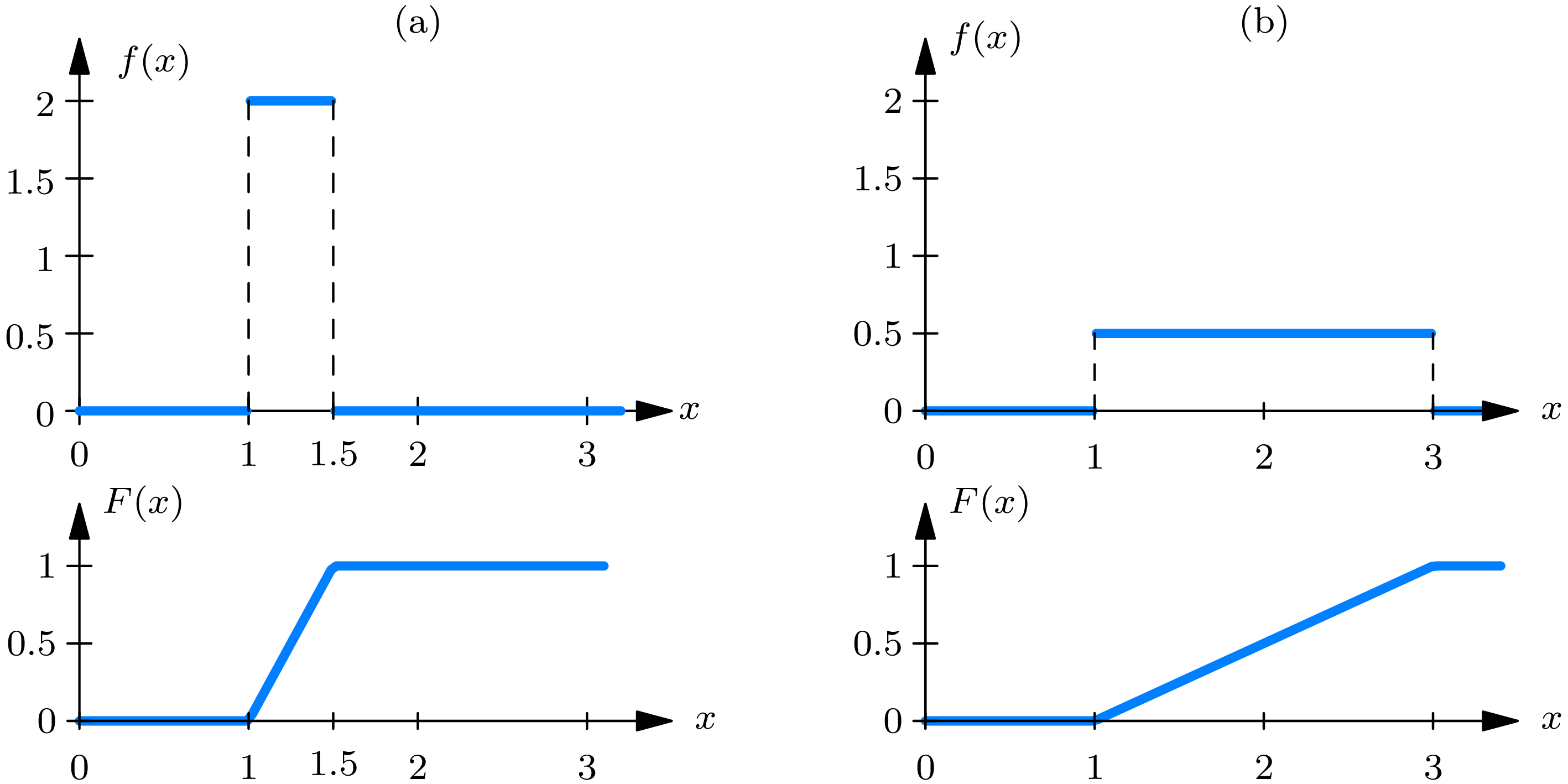
The distribution function \(F(\cdot)\) of a random phenomenon, which obeys a uniform probability law over the interval \(a\) to \(b\) is obtained from (5.1) :
\begin{align} F(x) = \begin{cases} 0, & \text{if } x \leq a \\[2mm] \frac{x-a}{b-a}, & \text{if } a \leq x \leq b \\[2mm] 1, & \text{if } x \geq b. \end{cases} \tag{5.3} \end{align}
By differentiation, the probability density function may be obtained:
\begin{align} f(x) = \begin{cases} \frac{1}{b-a}, & \text{if } a < x < b \\[2mm] 0, & \text{otherwise.} \end{cases} \tag{5.4} \end{align}
From (5.4) it follows that the definition of a uniform probability law given by (5.1) coincides with the definition given by (4.10) . (See (Fig. 5A) )
Example 5A . Waiting time for a train . Between 7 A.M. and 8 A.M. trains leave a certain station at \(3,5,8,10,13,15,18,20, \ldots\) minutes past the hour. What is the probability that a person arriving at the station will have to wait less than a minute for a train, assuming that the person’s time of arrival at the station obeys a uniform probability law over the interval of time (i) 7 A.M. to 8 A.M., (ii) 7:15 A.M. to 7: 30 A.M., (iii) 7:02 A.M. to 7:15 A.M., (iv) 7:03 A.M. to 7:15 A.M., (v) 7:04 A.M. to 7:15 A.M.?
Solution
We must first find the set \(B\) of real numbers in which the person’s arrival must lie in order for his waiting time to be less than 1 minute. One sees that \(B\) is the set of real numbers consisting of the intervals 2 to 3, 4 to 5, 7 to 8, 9 to 10, and so on. (See Fig. 5B .) The probability that the person will wait less than a minute for a train is given by \(P[B]\) , which is equal to, in the various cases, (i) \(\frac{24}{60}=\frac{2}{5}\) , (ii) \(\frac{6}{15}=\frac{2}{5}\) , (iii) \(\frac{6}{13}\) , (iv) \(\frac{5}{12}\) , (v) \(\frac{5}{11}\) .
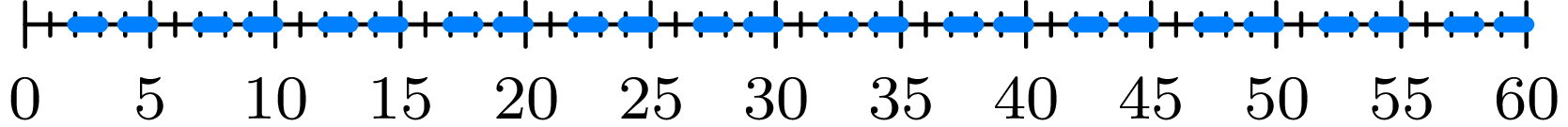
Example 5B . The probability law of the second digit in the decimal expansion of the square root of a randomly chosen number . A number is chosen from the interval 0 to 1 by a random mechanism that obeys a uniform probability law over the interval. What is the probability that the second decimal place of the square root of the number will be the digit 3? Is the digit \(k\) for \(k=0,1, \ldots, 9\) ?
Solution
For \(k=0,1, \ldots, 9\) let \(B_{k}\) be the set of numbers on the unit interval whose square roots have a second decimal equal to the digit \(k\) . A number \(x\) belongs to \(B_{k}\) if and only if \(\sqrt{x}\) satisfies for some \(m=0\) , \(1, \ldots, 9\)
\[m+\frac{k}{10} \leq 10 \sqrt{x}<m+\frac{k+1}{10}\]
or
\[\frac{1}{100}\left(m+\frac{k}{10}\right)^{2} \leq x<\frac{1}{100}\left(m+\frac{k+1}{10}\right)^{2} . \tag{5.5}\]
The length of the interval described by (5.5) is
\[\frac{1}{100}\left(m+\frac{k+1}{10}\right)^{2}-\frac{1}{100}\left(m+\frac{k}{10}\right)^{2}=\frac{1}{10,000}(20 m+2 k+1)\]
Hence the probability of the set \(B_{k}\) is given by
\[P\left[B_{k}\right]=\frac{1}{10,000} \sum_{m=0}^{9}(20 m+2 k+1)=0.091+0.002 k .\]
In particular, \(P\left[B_{3}\right]=0.097\) .
Exercises
5.1 . The time, measured in minutes, required by a certain man to travel from his home to a train station is a random phenomenon obeying a uniform probability law over the interval 20 to 25. If he leaves his home promptly at 7:05 A.M., what is the probability that he will catch a train that leaves the station promptly at 7:28 A.M.?
Answer
\(\frac{3}{5}\) .
5.2 . A radio station broadcasts the correct time every hour on the hour between the hours of 6 A.M. and 12 midnight. What is the probability that a listener will have to wait less than 10 minutes to hear the correct time if the time at which he tunes in is distributed uniformly over (chosen randomly from) the interval (i) 6 A.M. to 12 midnight, (ii) 8 A.M. to 6 P.M., (iii) 7:30 A.M. to 5:30 P.M., (iv) 7:30 A.M. to 5 P.M?
5.3 . The circumference of a wheel is divided into 37 arcs of equal length, which are numbered 0 to 36 (this is the principle of construction of a roulette wheel). The wheel is twirled. After the wheel comes to rest, the point on the wheel located opposite a certain fixed marker is noted. Assume that the point thus chosen obeys a uniform probability law over the circumference of the wheel. What is the probability that the point thus chosen will lie in an arc (i) with a number 1 to 10, inclusive, (ii) with an odd number, (iii) numbered 0?
Answer
(i) \(\frac{10}{3}\) ; (ii) \(\frac{1}{3} \frac{8}{7}\) ; (iii) \(\frac{1}{37}\) .
5.4 . A parachutist lands on the line connecting 2 towns, \(A\) and \(B\) . Suppose that the point at which he lands obeys a uniform probability law over the line. What is the probability that the ratio of his distance from \(A\) to his distance from \(B\) will be (i) greater than 3, (ii) equal to 3, (iii) greater than \(R\) , where \(R\) is a given real number?
5.5 . An angle \(\theta\) is chosen from the interval \(-\pi / 2\) to \(\pi / 2\) by a random mechanism that obeys a uniform probability law over the interval. A line is then drawn on an \((x, y)\) -plane through the point \((0,1)\) at the angle \(\theta\) with the \(y\) -axis. What is the probability, for any positive number \(z\) , that the \(x\) -coordinate of the point at which the line intersects the \(x\) -axis will be less than \(z\) ?
Answer
\(P[x<z]=P[\tan (-\theta)<z]=\frac{1}{2}+\frac{1}{\pi} \tan ^{-1} z\) .
5.6 . A number is chosen from the interval 0 to 1 by a random mechanism that obeys a uniform probability law over the interval. What is the probability that (i) its first decimal will be a 3, (ii) its second decimal will be a 3, (iii) its first 2 decimals will be 3’s, (iv) any specified decimal will be a 3, (v) any 2 specified decimals will be 3’s?
5.7 . A number is chosen from the interval 0 to 1 by a random mechanism that obeys a uniform probability law over the interval. What is the probability that (i) the first decimal of its square root will be a 3, (ii) the negative of its logarithm (to the base \(e\) ) will be less than 3?
Answer
(i) \(P[0.3<\sqrt{x}<0.4]=0.07\) ; (ii) \(P[-\ln x<3]=1-e^{-3}\) .