A basic problem of the theory of sampling is the following. An urn contains \(M\) balls, of which \(M_{W}\) are white (where \(M_{W}<M\) ) and \(M_{R}=\) \(M-M_{W}\) are red. A sample of size \(n\) is drawn either without replacement (in which case \(n \leq M\) ), or with replacement. Let \(k\) be an integer between 0 and \(n\) (that is, \(k=0,1,2, \ldots\) , or \(n\) ). What is the probability that the sample will contain exactly \(k\) white balls?
This problem is a prototype of many problems, which, as stated, do not involve the drawing of balls from an urn.
Example 3A . Acceptance sampling of a manufactured product . Consider the problem of acceptance sampling of a manufactured product . Suppose we are to inspect a lot of size \(M\) of manufactured articles of some kind, such as light bulbs, screws, resistors, or anything else that is manufactured to meet certain standards. An article that is below standard is said to be defective . Let a sample of size \(n\) be drawn without replacement from the lot. A basic role in the theory of statistical quality control is played by the following problem. Let \(k\) and \(M_{D}\) be integers such that \(k \leq n\) and \(M_{D} \leq M\) . What is the probability that the sample will contain \(k\) defective articles if the lot contains \(M_{D}\) defective articles? This is the same problem as that stated above, with defective articles playing the role of white balls.
Example 3B . A sample-minded game warden. Consider a fisherman who has caught 10 fish, 2 of which were smaller than the law permits to be caught. A game warden inspects the catch by examining two that he selects randomly from among the fish. What is the probability that he will not select either of the undersized fish? This problem is an example of those previously stated, involving sampling without replacement, with undersized fish playing the role of white balls, and \(M=10, M_{I V}=2\) , \(n=2, k=0\) . By (3.1) , the required probability is given by \(\left(\begin{array}{l}2 0\end{array}\right)(2)_{0}(8)_{2} /\) \((10)_{2}=28 / 45\) .
Example 3C . A sample-minded die . Another problem, which may be viewed in the same context but which involves sampling with replacement, is the following. Let a fair die be tossed four times. What is the probability that one will obtain the number 3 exactly twice in the four tosses? This problem can be stated as one involving the drawing (with replacement) of balls from an urn containing balls numbered 1 to 6, among which ball number 3 is white and the other balls, red (or, more strictly, nonwhite). In the notation of the problem introduced at the beginning of the section this problem corresponds to the case \(M=6, M_{I V}=1, n=4, k=2\) . By (3.2) , the required probability is given by \(\left(\begin{array}{l}4 \\ 2\end{array}\right)(1)^{2}(5)^{2} /(6)^{4}=25 / 216\) .
To emphasize the wide variety of problems, of which that stated at the beginning of the section is a prototype, it may be desirable to avoid references to white balls in the statement of the solution of the problem (although not in the statement of the problem itself) and to speak instead of scoring “successes”. Let us say that we score a success whenever we draw a white ball. Then the problem can be stated as that of finding, for \(k=0,1, \ldots, n\) , the probability of the event \(A_{k}\) that one will score exactly \(k\) successes when one draws a sample of size \(n\) from an urn containing \(M\) balls, of which \(M_{W}\) are white. We now show that in the case of sampling without replacement \[P\left[A_{k}\right]=\left(\begin{array}{l} n \tag{3.1} \\ k \end{array}\right) \frac{\left(M_{W}\right)_{k}\left(M-M_{W}\right)_{n-k}}{(M)_{n}}, \quad k=0,1, \ldots, n.\] whereas in the case of sampling with replacement \[P\left[A_{k}\right]=\left(\begin{array}{l} n \tag{3.2} \\ k \end{array}\right) \frac{\left(M_{W}\right)^{k}\left(M-M_{W}\right)^{n-k}}{M^{n}}, \quad k=0,1, \ldots, n.\]
It should be noted that in sampling without replacement if the number \(M_{Y^{r}}\) of white balls in the urn is less than the size \(n\) of the sample drawn then clearly \(P\left[A_{k}\right]=0\) for \(k=M_{I}+1, \ldots, n\) . Equation (3.1) embodies this fact, in view of (1.10) .
Before indicating the proofs of (3.1) and (3.2) , let us state some useful alternative ways of writing these formulas. For many purposes it is useful to express (3.1) and (3.2) in terms of \[p=\frac{M_{\mathrm{W}}}{M}, \tag{3.3}\] the proportion of white balls in the urn. The formula for \(P\left[A_{k}\right]\) can then be compactly written, in the case of sampling with replacement, \[P\left[A_{k}\right]=\left(\begin{array}{l} n \tag{3.4} \\ k \end{array}\right) p^{k}(1-p)^{n-k}.\]
Equation (3.4) is a special case of a very general result, called the binomial law, which is discussed in detail in section 3 of Chapter 3. The expression given by (3.1) for the probability of \(k\) successes in a sample of size \(n\) drawn without replacement may be expressed in terms of \(p\) by \begin{align} P & \left[A_{k}\right]={n\choose k} p^{k}(1-p)^{n-k} \\ & \times \frac{\left[\begin{array}{r} \left(1-\frac{1}{M_{W}}\right)\left(1-\frac{2}{M_{W}}\right) \cdots\left(1-\frac{k-1}{M_{W}}\right)\left(1-\frac{1}{M-M_{W}}\right) \\ \times\left(1-\frac{2}{M-M_{W}}\right) \cdots\left(1-\frac{n-k-1}{M-M_{T W}}\right) \end{array}\right]}{\left(1-\frac{1}{M}\right)\left(1-\frac{2}{M}\right) \cdots\left(1-\frac{n-1}{M}\right)}. \end{align} Consequently, one sees that in the case in which \(k / M_{W W},(n-k) /\) \(\left(M-M_{W}\right)\) , and \(n / M\) are small (say, less than 0.1) then the probability of the event \(A_{k}\) is approximately the same in sampling without replacement as it is in sampling with replacement.
Another way of writing (3.1) is in the computationally simpler form \[P\left[A_{k}\right]=\frac{\left(\begin{array}{c} M_{W} \tag{3.6} \\ k \end{array}\right)\left(\begin{array}{c} M-M_{W} \\ n-k \end{array}\right)}{\left(\begin{array}{c} M \\ n \end{array}\right)}.\]
It may be verified algebraically that (3.1) and (3.6) agree. In section 5 we discuss the intuitive meaning of (3.6) .
We turn now to the proof of (3.1) . Let the balls in the urn be numbered 1 to \(M\) , the white balls bearing numbers 1 to \(M_{W}\) . The sample description space \(S\) then consists of \(n\) -tuples \(\left(z_{1}, z_{2}, \ldots, z_{n}\right)\) , in which, for \(i=\) \(1, \ldots, n, z_{i}\) is a number 1 to \(M\) , subject to the condition that no two components of an n-tuple may be the same. The size of \(S\) is given by \(N[S]=(M)_{n}\) . The event \(A_{k}\) consists of all sample descriptions in \(S\) , exactly \(k\) components of which are numbers 1 to \(M_{T V}\) . To compute the size of \(A_{k}\) , we first compute the size of events \(B\) of the following form. Let \(J=\left\{j_{1}, j_{2}, \ldots, j_{k}\right\}\) be a subset of size \(k\) of the set of integers \(\{1,2, \ldots, n\}\) . Define \(B_{J}\) as the event that white balls are drawn in and only in those draws whose draw numbers are in \(J\) ; that is, \(B_{J}\) is the set of descriptions \(\left(z_{1}, z_{2}, \ldots, z_{n}\right)\) whose \(j_{1}\) st, \(j_{2}\) nd, \(\ldots, j_{k}\) th components are numbers 1 to \(M_{W}\) and whose remaining components are numbers \(M_{W}+1\) to \(M\) . The size of \(B_{J}\) may be obtained immediately by means of the basic principle of combinatorial analysis. We obtain \(N\left[B_{J}\right]=\left(M_{W}\right)_{k}\left(M-M_{W}\right)_{n-k}\) , since there are \(\left(M_{\mathrm{W}}\right)_{k}\) ways in which white balls may be assigned to the \(k\) components of a description in \(B_{J}\) in which white balls occur and \(\left(M-M_{W}\right)_{n-k}\) ways in which nonwhite balls may be assigned to the remaining \((n-k)\) components. Now, by (1.8) , there are \(\left(\begin{array}{l}n \\ k\end{array}\right)\) subsets of size \(k\) of the integers \(\{1,2, \ldots, n\}\) . For any two such subsets \(J\) and \(J^{\prime}\) the corresponding events \(B_{J}\) and \(B_{J}\) are mutually exclusive. Further, the event \(A\) may be regarded as the union, over such subsets \(J\) , of the events \(B_{J}\) . Consequently, the size of \(A\) is given by \(N[A]=\left(\begin{array}{l}n \\ k\end{array}\right)\left(M_{W}\right)_{k}\left(M-M_{W}\right)_{n-k}\) . If we assume that all the descriptions in \(S\) are equally likely, we obtain (3.1) . To prove (3.2) , we use a similar argument.
Example 3D . The difference between \(k\) successes and successes on \(k\) specified draws . Let a sample of size 3 be drawn without replacement from an urn containing six balls, of which four are white. The probability that the first and second balls drawn will be white and the third ball black is equal to \((4)_{2}(2)_{1} /(6)_{3}\) . However, the probability that the sample will contain exactly two white balls is equal to \(\left(\begin{array}{l}3 \\ 2\end{array}\right)(4)_{2}(2)_{1} /(6)_{3}\) . If the sample is drawn with replacement, then the probability of white balls on the first and second draws and a black ball on the third is equal to \((4)^{2}(2)^{1} /(6)^{3}\) , whereas the probability of exactly two white balls in the sample is equal to \(\left(\begin{array}{l}3 \\ 2\end{array}\right)(4)^{2}(2)^{1} /(6)^{3}\) .
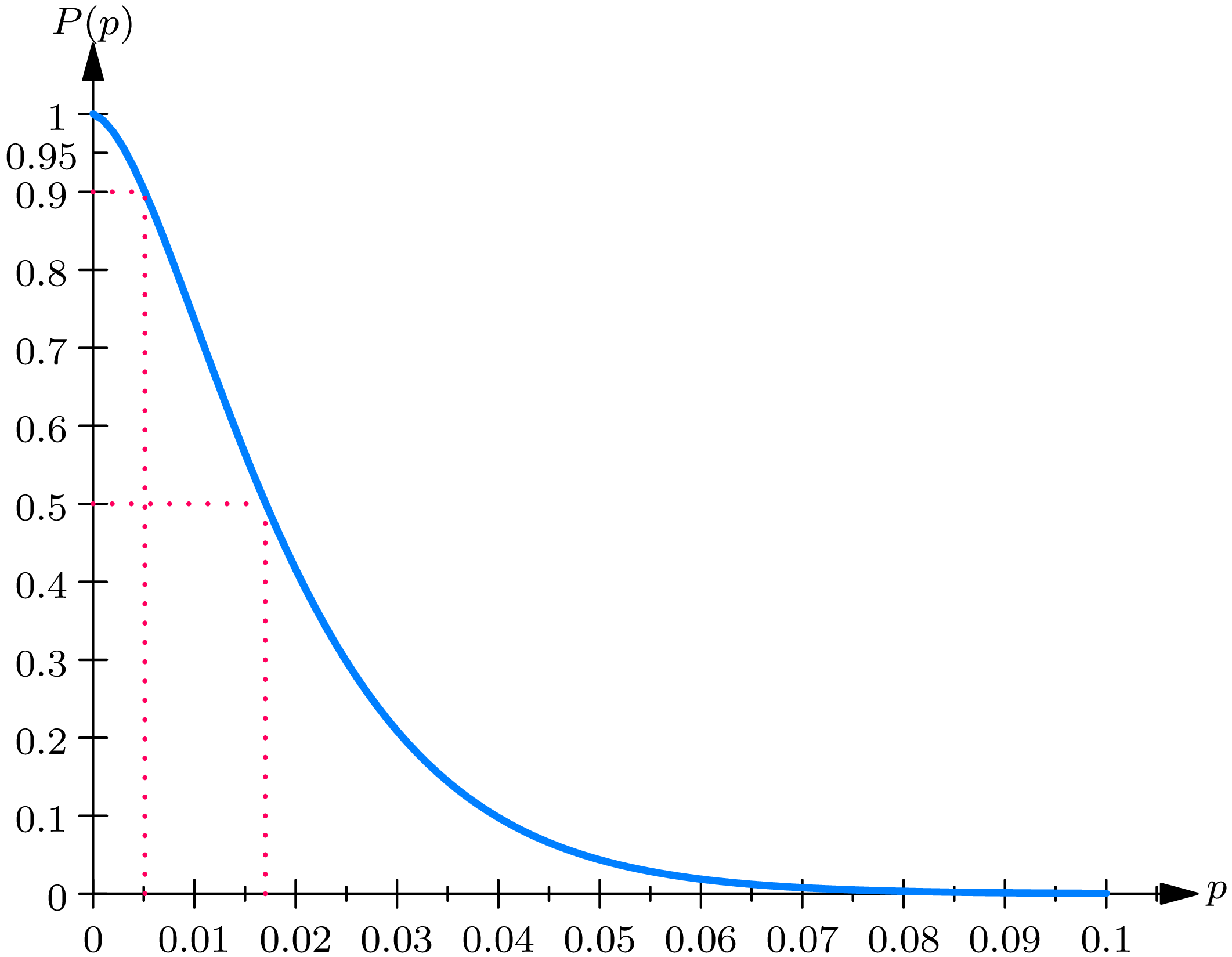
Example 3E . Acceptance sampling. Suppose that we wish to inspect a certain product by means of a sample drawn from a lot. Probability theory cannot tell us how to constitute a lot or how to inspect the sample or even how large a sample to draw. Rather, probability theory can tell us the consequences of certain actions, given that certain assumptions are true. Suppose we decide to inspect the product by forming lots of size 1000, from which we will draw a sample of size 100. Each of the items in the sample is classified as defective or non-defective. It is unreasonable to demand that the lot be perfect. Consequently, we may decide to accept the lot if the sample contains one or fewer defectives and to reject the lot if two or more of the items inspected are defective. The question naturally arises as to whether this acceptance scheme is too lax or too stringent; perhaps we ought to demand that the sample contain no defectives, or perhaps we ought to permit the sample to contain two or fewer defectives. In order to decide whether or not a given acceptance scheme is suitable, we must determine the probability \(P\) that a randomly chosen lot will be accepted. However, we do not possess sufficient information to compute \(P\) . In order to compute the probability \(P\) of acceptance of a lot, using a given acceptance sampling plan, we must know the proportion \(p\) of defectives in a lot. Thus \(P\) is a function of \(p\) , and we write \(P(p)\) to denote the probability of acceptance of a lot in which the proportion of defectives is \(p\) . Now for the acceptance sampling plan, which consists in drawing a sample of size 100 from a lot of size 1000 and accepting it if the lot contains one or fewer defectives, \(P(p)\) is given by \[P(p)=\frac{(1000 q)_{100}}{(1000)_{100}}+100 \frac{1000 p(1000 q)_{99}}{(1000)_{100}}, \tag{3.7}\] where we have let \(q=1-p\) . The graph of \(P(p)\) as a function of \(p\) is called the operating characteristic curve, or OC curve, of the acceptance sampling plan. In Fig. 3A we have plotted the OC curve for the sampling scheme described. We see that the probability of accepting a lot is 0.95 if it contains \(0.4 \%\) defective items, whereas the probability of accepting a lot is only 0.50 if it contains \(1.7 \%\) defective items.
Example 3F . Winning a prize in a Lottery . Consider a lottery that sells \(n^{2}\) tickets and awards \(n\) prizes. If one buys \(n\) tickets, what is the probability of winning a prize?
Solution
The probability \(P_{1}\) of winning a prize is related to the probability \(P_{0}\) of not winning a prize by \(P_{1}=1-P_{0}\) . Now \(P_{0}\) is the probability that a sample of size \(n\) drawn without replacement from an urn containing \(n^{2}\) tickets will not contain any of \(n\) specified tickets. Consequently, \[P_{0}=\frac{\left(n^{2}-n\right)_{n}}{\left(n^{2}\right)_{n}}. \tag{3.8}\]
In the case that \(n=10, P_{0}=(90)_{10} /(100)_{10}=0.330\) , so that \(P_{1}=0.670\) . In the case that \(n\) is large it may be shown approximately, that, \[P_{0}=\frac{1}{e}=(2.718)^{-1}=0.368, \quad P_{1}=1-e^{-1}=0.632. \tag{3.9}\]
In the foregoing we have considered the problem of drawing a sample from an urn containing balls of only two colors. However, one may desire to consider urns containing balls of more than two colors. In theoretical exercises 3.1 to 3.3 we obtain formulas for this case. The following example illustrates the ideas involved.
Example 3G . Sampling from three plumbers . Consider a town in which there are three plumbers, whom we call \(A, B\) , and \(C\) . On a certain day six residents of the town telephone for a plumber. If each resident selects a plumber at random from the telephone directory, what is the probability that three residents will call \(A\) , two residents will call \(B\) , and one resident will call \(C\) ?
Solution
For \(j=1,2, \ldots, 6\) let \(z_{j}=A, B\) , or \(C\) , depending on whether the plumber called by the \(j\) th resident is \(A, B\) , or \(C\) . The sample description space \(S\) of the observation is then a space of 6-tuples, \(S=\left\{\left(z_{1}, z_{2}, \ldots, z_{6}\right)\right.\) : for \(j=1, \ldots, 6, z_{j}=A, B\) , or \(\left.C\right\}\) . Clearly, \(N[S]=3^{6}\) . Next, the event \(E\) that three residents call \(A\) , two call \(B\) , and one calls \(C\) has size
\[N[E] = { 6 \choose 321} = \frac{6!}{3! \; 2! \; 1!} = 60, \tag{3.10}\]
so that \(P[E]=60 / 3^{6}=0.082\) . To prove (3.10) , we note that the number of samples of size 6, which contain three calls for \(A\) , two calls for \(B\) , and one call for \(C\) , is the number of ways one can partition the set \(\{1,2,3,4,5,6\}\) into three ordered subsets of sizes 3,2, and 1, respectively.
Theoretical Exercises
3.1 . Consider an urn containing \(M\) balls of \(r\) different colors. Let \(M_{1}\) , \(M_{2}, \ldots, M_{r}\) denote, respectively, the number of balls of color 1, color \(2, \ldots\) , color \(r\) . Show the probability that a sample of size \(n\) will contain \(k_{1}\) balls of color \(1, k_{2}\) balls of color \(2, \ldots, k_{r}\) balls of color \(r\) , where \(k_{1}+k_{2}+\cdots+k_{r}=n\) , in the case of sampling with replacement is given by \[\left(\begin{array}{c} n \tag{3.11} \\ k_{1} k_{2} \cdots k_{r} \end{array}\right) \frac{\left(M_{1}\right)^{k_{1}}\left(M_{2}\right)^{k_{2}} \cdots\left(M_{r}\right)^{k_{r}}}{(M)^{n}}.\] and, in the case of sampling without replacement, is given by \[\left(\begin{array}{c} n \tag{3.12} \\ k_{1} k_{2} \cdots k_{r} \end{array}\right) \frac{\left(M_{1}\right)_{k_{1}}\left(M_{2}\right)_{k_{2}} \cdots\left(M_{r}\right)_{k_{r}}}{(M)_{n}}.\] Hint: The number of samples of size \(n\) that contain \(k_{1}\) balls of color 1, \(k_{2}\) balls of color \(2, \ldots, k_{r}\) balls of color \(r\) is equal to the number of ways one can partition a set of size \(n\) into \(r\) ordered subsets of sizes \(k_{1}, k_{2}, \ldots\) , \(k_{r}\) , respectively.
3.2 . Show that, in terms of the proportions
\[p_{1}=\frac{M_{1}}{M}, \quad p_{2}=\frac{M_{2}}{M}, \ldots, p_{r}=\frac{M_{r}}{M}, \tag{3.13}\]
one may express (3.11) by
\[\left(\begin{array}{c} n \\ k_1 k_2 \cdots k_r \end{array}\right) p_{1}^{k_{1}} p_{2}^{k_{2}} \cdots p_{r}^{k_{r}}.\tag{3.14}\]
3.3 . Consider an urn containing \(n\) balls, each of a different color. Let \(r\) be any integer. Show the probability that a sample of size \(r\) drawn with replacement will contain \(r_{1}\) balls of color \(1, r_{2}\) balls of color \(2, \ldots, r_{n}\) balls of color \(n\) , where \(r_{1}+r_{2}+\cdots+r_{n}=r\) is given by \[\frac{1}{n^{r}}\left(\begin{array}{c} r \\ r_{1} r_{2} \cdots r_{n} \end{array}\right).\]
3.4 . An urn contains \(M\) balls, numbered 1 to \(M\) . Let \(N\) numbers be designated “lucky,” where \(N \leq M\) . Let a sample of size \(n\) be drawn either without replacement (in which case \(n \leq M\) ), or with replacement. Show that the probability that the sample will contain exactly \(k\) balls with “lucky” numbers is given by (3.1) and (3.2) , respectively, with \(M_{W}\) replaced by \(N\) .
Exercises
3.1 . An urn contains 52 balls, numbered 1 to 52. Suppose that numbers 1 through 13 are considered “lucky”. A sample of size 2 is drawn from the urn with replacement (without replacement). What is the probability that (i) both balls drawn will be “lucky,” (ii) neither ball drawn will be “lucky,” (iii) at least 1 of the balls drawn will be “lucky,” (iv) exactly 1 of the balls drawn will be “lucky”?
Answer
With replacement (i) \(\frac{1}{18}\) , (ii) \(\frac{9}{16}\) , (iii) \(\frac{2}{16}\) , (iv) \(\frac{3}{8}\) ; without replacement (i) \(\frac{1}{17}\) , (ii) \(\frac{19}{34}\) , (iii) \(\frac{15}{34}\) , (iv) \(\frac{13}{34}\) .
3.2 . An urn contains 52 balls, numbered 1 to 52. Suppose that the numbers \(1,14,27\) , and 40 are considered “lucky”. A sample of size 13 is drawn from the urn with replacement (without replacement). What is the probability that the sample will contain (i) exactly 1 “lucky” number, (ii) at least 1 lucky number, (iii) exactly 4 “lucky” numbers?
3.3 . A man tosses a fair coin 10 times. Find the probability that he will have (i) heads on the first 5 tosses, tails on the second 5 tosses, (ii) heads on tosses \(1,3,5,7,9\) , tails on tosses \(2,4,6,8,10\) , (iii) 5 heads and 5 tails, (iv) at least 5 heads, (v) no more than 5 heads.
Answer
(i), (ii) \(2^{-10}\) ; (iii) \(\frac{126}{512}\) ; (iv), (v) \(\frac{319}{512}\) .
3.4 . A group of \(n\) men toss fair coins simultaneously. Find the probability that the \(n\) coins (i) are all heads, (ii) are all tails, (iii) contain exactly 1 head, (iv) contain exactly 1 tail, (v) are all alike. Evaluate these probabilities for \(n=2,3,4,5\) .
3.5 . Consider 3 urns; urn I contains 2 white and 4 red balls, urn II contains 8 white and 4 red balls, urn III contains 1 white and 3 red balls. One ball is selected from each urn. Find the probability that the sample drawn will contain exactly 2 white balls.
Answer
\(\frac{11}{36}\) .
3.6 . A box contains 24 bulbs, 4 of which are known to be defective and the remainder of which is known to be non-defective. What is the probability that 4 bulbs selected at random from the box will be non-defective?
3.7 . A box contains 50 razor blades, 5 of which are known to be used, the remainder unused. What is the probability that 5 razor blades selected from the box will be unused?
Answer
\((45)_{5} /(50)_{5}\) .
3.8 . A fisherman caught 10 fish, 3 of which were smaller than the law permits to be caught. A game warden inspects the catch by examining 2, which he selects at random among the fish. What is the probability that he will not select any undersized fish?
3.9 . A professional magician named Sebastian claimed to be able to “read minds”. In order to test his claims, an experiment is conducted with 5 cards, numbered 1 to 5. A person concentrates on the numbers of 2 of the cards, and Sebastian attempts to “read his mind” and to name the 2 cards. What is the probability that Sebastian will correctly name the 2 cards, under the assumption that he is merely guessing?
Answer
\(0.1\) .
3.10 . Find approximately the probability that a sample of 100 items drawn from a lot of 1000 items contains 1 or fewer defective items if the proportion of the lot that is defective is (i) 0.01, (ii) 0.02, (iii) 0.05.
3.11 . The contract between a manufacturer of electrical equipment (such as resistors or condensors) and a purchaser provides that out of each lot of 100 items 2 will be selected at random and subjected to a test. In negotiations for the contract the following two acceptance sampling plans are considered. Plan (a): reject the lot if both items tested are defective; otherwise accept the lot. Plan \((b)\) : accept the lot if both items tested are good; otherwise reject the lot. Obtain the operating characteristic curves of each of these plans. Which plan is more satisfactory to (i) the purchaser, (ii) the manufacturer? If you were the purchaser, would you consider either of the plans acceptable?
Answer
Manufacturer would prefer plan (a), consumer would prefer plan (b).
3.12 . Consider a lottery that sells 25 tickets, and offers (i) 3 prizes, (ii) 5 prizes. If one buys 5 tickets, what is the probability of winning a prize?
3.13 . Consider an electric fixture (such as Christmas tree lights) containing 5 electric light bulbs which are connected so that none will operate if any one of them is defective. If the light bulbs in the fixture are selected randomly from a batch of 1000 bulbs, 100 of which are known to be defective, find the probability that all the bulbs in the electric fixture will operate.
Answer
\((900)_{5} /(1000)_{5} \doteq (0.9)^{5}=0.59\) .
3.14 . An urn contains 52 balls, numbered 1 to 52. Find the probability that a sample of 13 balls drawn without replacement will contain (i) each of the numbers 1 to 13, (ii) each of the numbers 1 to 7.
3.15 . An urn contains balls of 4 different colors, each color being represented by the same number of balls. Four balls are drawn, with replacement. What is the probability that at least 3 different colors are represented in the sample?
Answer
\(\frac{21}{32}\) .
3.16 . From a committee of 3 Romans, 4 Babylonians, and 5 Philistines a subcommittee of 4 is selected by lot. Find the probability that the committee will consist of (i) 2 Romans and 2 Babylonians, (ii) 1 Roman, 1 Babylonian, and 2 Philistines; (iii) 4 Philistines.
3.17 . Consider a town in which there are 3 plumbers; on a certain day 4 residents telephone for a plumber. If each resident selects a plumber at random from the telephone directory, what is the probability that (i) all plumbers will be telephoned, (ii) exactly 1 plumber will be telephoned?
Answer
(i) \(\frac{4}{9}\) , (ii) \(\frac{1}{27}\) .
3.18 . Six persons, among whom are \(A\) and \(B\) , are arranged at random (i) in a row, (ii) in a ring. What is the probability that (a) \(A\) and \(B\) will stand next to each other, (b) \(A\) and \(B\) will be separated by one and only one person?