1. Two people grab a rope and pull it in opposite directions. One of them overpowers the other. Does this mean that the first person applies a greater force to the rope than the second? Compare the work done by the forces applied to the rope.
Answer
The forces are equal in magnitude; the works are also equal in magnitude but opposite in sign, because in one case the direction of the force acting on the rope and its displacement coincide, while in the other case they are opposite.
2. What is the work $A$ required to lift a chain, taken by one end and lying on a plane, to a height equal to its length? The chain has a length $l = 2 \, \text{m}$ and a mass $m = 5 \, \text{kg}$.
Answer
$A = mg \frac{l}{2} \approx 50$ J.
Hint
The work done is equal to the work done in lifting the center of gravity of the chain.
3. A window shade with a mass $M = 1 \, \text{kg}$ and length $l = 2 \, \text{m}$ rolls up onto a thin roller at the top of the window. What work is done in this process? Neglect friction.
Answer
$A = Mg \frac{l}{2} \approx 10$ J.
4. A flexible rubber hose of length $l$ hangs such that one end is $\frac{1}{3} l$ lower than the other. The hose is filled with the maximum possible amount of water, with density $\rho$. What is the minimal work needed to pour the water out of the hose by lifting its lower end while keeping the upper end at a constant height? The inner diameter of the hose is $d$. Neglect the mass of the hose. The radius of curvature of the hose bend is much smaller than $l$.
Answer
$A = \frac{\rho g l^2 \pi a^2}{12}$.
Hint
The work goes into lifting the center of mass of the water in the hose from a height of $\frac{1}{6}l$ to a height of $\frac{2}{3}l$.
5. A chain of mass $M$ and length $l$ lies at the boundary of two adjoining half-planes made of different materials (see figure). What work must be done to move the chain onto the second half-plane? The coefficients of friction between the chain and the half-planes are $k_1$ and $k_2$, respectively. Solve the problem graphically as well. 
Answer
$A = \frac{1}{2}(k_1 + k_2) Mgl$.
Solution
The friction force overcome when moving the chain is: $\begin{aligned} F_{fr} &= F_1 + F_2 \\ &= k_1 \frac{Mg}{l}(l - x) + k_2 \frac{Mg}{l} x \\ &= k_1 Mg - \frac{Mg}{l}(k_1 - k_2) x \end{aligned},$ where $x$ is the distance from the boundary between the semi-planes to the beginning of the chain. The graph of the dependence of the friction force on the displacement of the chain is shown below. The work done is numerically equal to the area of the figure bounded above by the graph of the force, i.e. $A = \frac{1}{2}(k_1 + k_2) Mgl.$
The problem can also be solved by plotting the graphs of the dependence of the friction force on the displacement of the chain on each of the semi-planes and determining the total area of the resulting figures.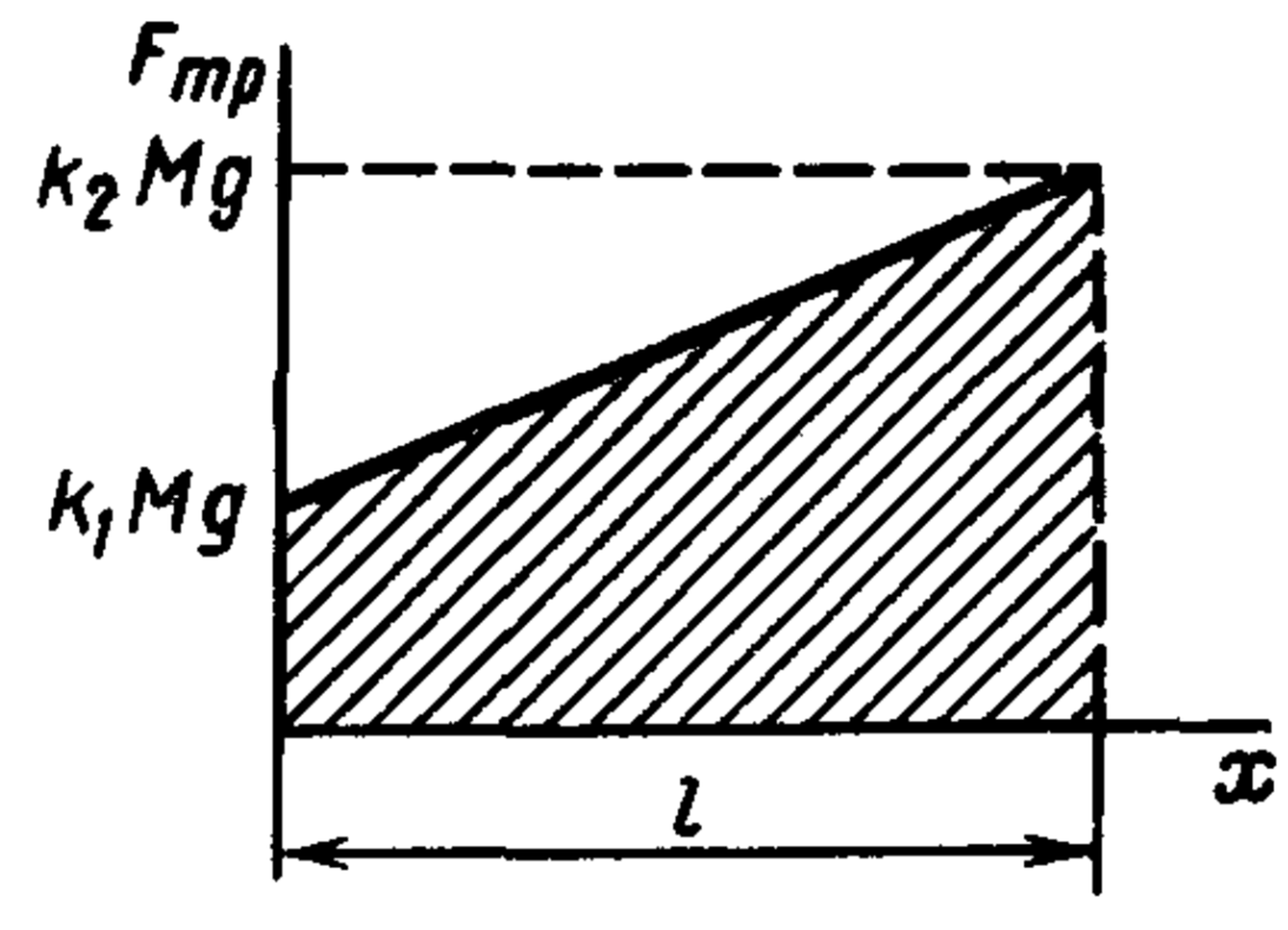
6. An engine with a useful power of 15 kW, installed on a car, can propel it at a speed of 90 km/h on a horizontal road. The same engine, installed on a motorboat, ensures a speed no greater than 15 km/h. Determine the resistance force $F_c$ acting on the car and the motorboat at the given speeds.
Answer
$F_{c1} = 600$ H; $F_{c2} = 3600$ H.
7. A tram of mass $M$ moves uphill at a constant speed on a street inclined at an angle $\alpha$ to the horizon. On a horizontal section, it can pull an additional car of mass $M_1$ at the same speed. What is the mass $M_1$ if the rolling friction coefficient of the wheels is $k$? The engine power is constant.
Answer
$M_1 = M \left( \frac{\sin \alpha}{k} + \cos \alpha - 1 \right)$.
Hint
Power is equal to $N = Fv$ (where F is the traction force, v is the speed). Since the speeds are the same in both cases, the traction forces developed by the wagon's engine are also the same: $Mg \sin \alpha + kMg \cos \alpha = (M + M_1)gk$.
8. A locomotive, operating at constant power, can pull a train of mass $M = 2000$ tonnes uphill on a slope of $\alpha_1 = 0.005$ at a speed $v_1 = 30$ km/h or on a slope of $\alpha_2 = 0.0025$ at a speed $v_2 = 40$ km/h. Determine the resistance force $F_c$, assuming it is constant.
Answer
$F_c = \dfrac{Mg (v_1 \sin \alpha_1 - v_2 \sin \alpha_2)}{v_2 - v_1} \approx 9800$ H.
Hint
The power of the locomotive (see previous problem) $N = (Mg \sin \alpha_1 + F_c) v_1 = (Mg \sin \alpha_2 + F_c) v_2.$
9. A bullet flying at a certain speed penetrates a wall to a depth $l_1 = 10$ cm. To what depth $l_2$ will the bullet penetrate the same wall if its speed is doubled?
Answer
$l_2 = 40$ cm.
10. A bullet flying at speed $v_0$ pierces several identical boards placed at some distance from each other. In which board (counted from the first) will the bullet get stuck if its speed after passing the first board is $v_1 = 0.83 v_0$?
Answer
In the fourth board.
Hint
The kinetic energy losses of the bullet when passing through each board are identical and equal to: $\Delta E = \frac{m v_0^2}{2} - \frac{m v_1^2}{2} = \frac{m (v_0^2 - v_1^2)}{2}.$ The bullet will lose all its energy after piercing $n = \frac{mv_0^2/2}{\Delta E} = \frac{v_0^2}{v_0^2 - v_1^2} \approx 3.3\text{ boards},$ i.e., the bullet will get stuck in the fourth board.
11. What work must be done to make a train of mass $M = 800$ tonnes: a) increase its speed from $v_1 = 36$ km/h to $v_2 = 54$ km/h; b) stop when the initial speed is $v_3 = 72$ km/h? Neglect resistance.
Answer
a) $A_1 = \frac{M v_1^2}{2} - \frac{M v_0^2}{2} = 5 \cdot 10^4$ kJ;
b) $A_2 = mv_0^2/2 = 1.6 \cdot 10^5$ kJ.
12. A train of mass $M = 2000$ tonnes, starting from rest with an acceleration $a = 0.2 \, \text{m/s}^2$, reaches the desired speed in one minute and then moves uniformly. Determine the power of the locomotive during steady motion if the resistance coefficient $k = 0.005$.
Answer
$N = Mgkat \approx 1.2 \cdot 10^6$ W.
13. A car of mass $M = 2000$ kg starts from rest and moves uphill on a slope of $\alpha = 0.02$. After traveling a distance $s = 100$ m, it reaches a speed $v = 32.4$ km/h. The resistance coefficient is $k = 0.05$. Determine the average power developed by the car's engine.
Answer
$N_{avg} = M \left( \frac{v^2}{2s} + ga + kg \right) \frac{v}{2} \approx 9900$ W (assuming $\sin \alpha \approx \alpha, \cos \alpha \approx 1$).
14. A rocket of mass $M$ hovers motionless above Earth with its engine running. The speed of the exhaust gases is $u$. Determine the engine's power.
Answer
$N = Mgu/2$.
Hint
The engine power is $N = \mu u^2 / 2$, where $\mu$ is the fuel consumption rate. The reactive force $\mu u$ balances the force of gravity: $\mu u = Mg$.
15. In which case must the car's engine do more work: accelerating from rest to a speed of 27 km/h or increasing the speed from 27 km/h to 54 km/h? Assume the resistance force and acceleration time are the same in both cases.
Answer
In the second case: $A_2 / A_1 = 3$.
Hint
Since the accelerations of the car and the resistance forces are the same in both cases, the traction forces $F_T$, equal to $ma + F_{res}$, are also equal. However, the distance traveled by the car in the second case is three times greater.
16. A stone of mass $m = 200$ g is thrown from a horizontal surface at an angle to the horizon and lands back on the surface at a distance $s = 5$ m after $t = 1.2$ s. Find the work done during the throw. Neglect air resistance.
Answer
$A = \dfrac{m}{2} \left( \dfrac{g^2 t^4}{4} + \dfrac{l^2}{t^2} \right) \approx 5.2$ J.
Hint
The work is spent on giving the body kinetic energy.
17. Determine the work required to compress a spring by $x = 10$ cm if a force $F_0 = 100 \, \text{N}$ is needed to compress it by $x_0 = 1$ cm.
Answer
$A = \frac{F_0 x^2}{2 x_0} = 50$ J.
Solution
The work done in compressing the spring can be found by plotting the graph of the dependence of the force $F$ acting on the spring on the magnitude of its deformation $x$, i.e., on the displacement of the end of the spring from its equilibrium position. According to Hooke's law, this force is $F = kx$, where $k$ is the spring constant, which in this case is $k = F_0/x_0 = 10^4$ N/m. The work of compressing the spring will be numerically equal to the area of the triangle OAB (see figure): $A = \frac{kx \cdot x}{2} = \frac{kx^2}{2} = \frac{F_0}{x_0} \frac{x^2}{2} = 50 \text{ J}.$ 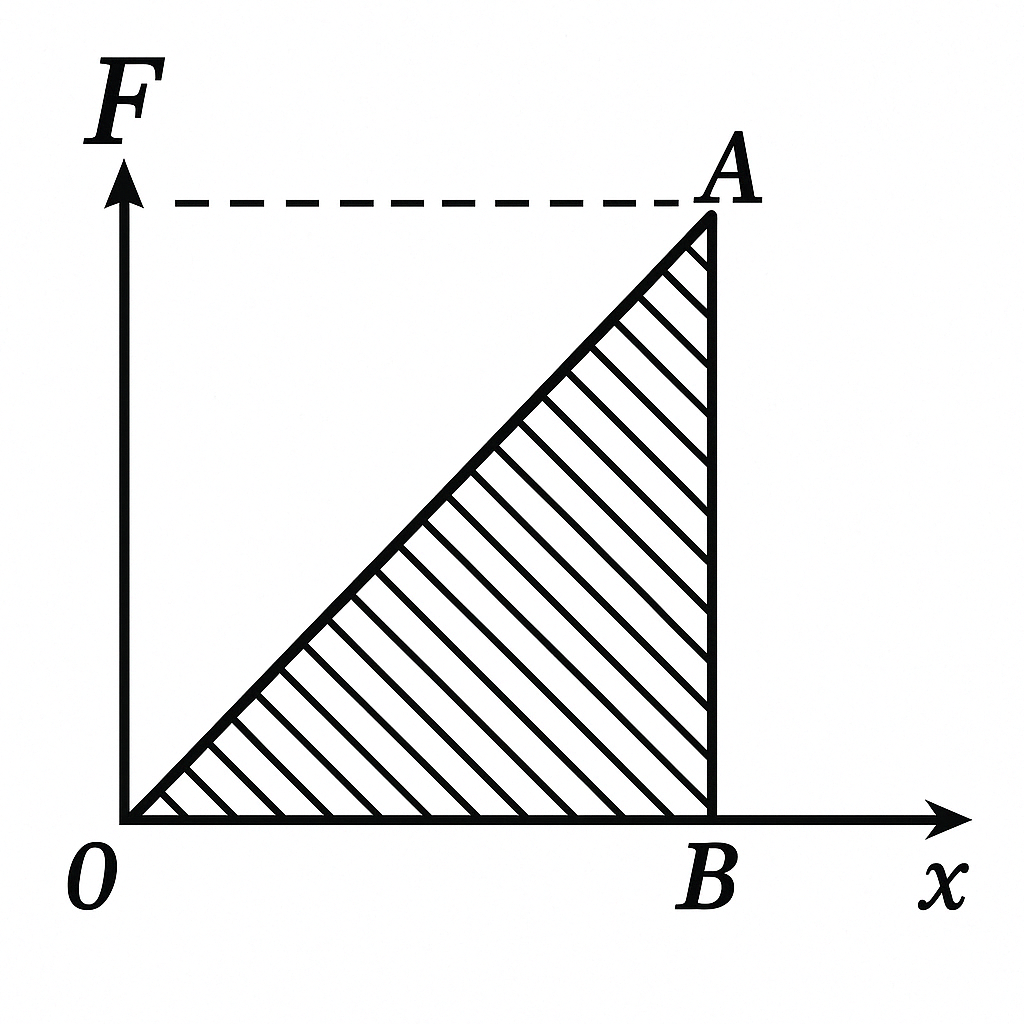
18. A railcar of mass $M = 2 \cdot 10^4 \, \text{kg}$, moving at a speed $v = 0.5 \, \text{m/s}$, collides with two stationary spring buffers. Find the maximum compression $x$ of the buffers if a force of $5 \cdot 10^4 \, \text{N}$ compresses a buffer by 1 cm. Neglect friction.
Answer
$x \approx 2.2$ cm.
Hint
Upon impact, the kinetic energy of the wagon is converted into the work of compressing the springs, i.e., it transforms into their potential energy: $W_p = 2 kx^2 / 2$, where $k = 5 \cdot 10^6$ N/m (see problem 17).
19. A constant force $F = 200 \, \text{N}$ lifts a load of mass $M = 10 \, \text{kg}$ to a height $h = 10 \, \text{m}$. What work $A$ does the force $F$ perform? What potential energy $U$ will the lifted load possess?
Answer
$A = Fh = 2 \cdot 10^3$ J; $\Pi = mgh = 10^3$ J. The body also possesses kinetic energy $T = A - \Pi$.
20. An elevator of mass $M = 1000 \, \text{kg}$ is accelerated upward by a winch. Over a segment of the path of length $l = 1 \, \text{m}$, the elevator moves at an average speed $v_{\text{avg}} = 5 \, \text{m/s}$, and its speed increases by $\Delta v = 0.5 \, \text{m/s}$. What work is done by the force moving the elevator over this segment?
Answer
$A = Mgl + Mv_{avg} \Delta v = 12.3 \cdot 10^3$ J.
Hint
$\frac{v_1^2 - v_2^2}{2} = \frac{v_1 + v_2}{2} (v_1 - v_2) = v_{avg} \Delta v.$
21. What work will a force $F = 30 \, \text{N}$ do by lifting a load of mass $m = 2 \, \text{kg}$ up an inclined plane to a height $h = 2.5 \, \text{m}$ with an acceleration $a = 10 \, \text{m/s}^2$? The force acts parallel to the inclined plane. Neglect friction.
Answer
$mgh \dfrac{F}{F - ma} \approx 147$ J.
Hint
The work goes into increasing the potential energy of the load $mgh$ and imparting kinetic energy $\frac{mv^2}{2}$. $\frac{mv^2}{2} = \frac{mah}{\sin \alpha} = \frac{mah}{h/l} = mal.$ It can also be calculated simply using the formula $A = Fl = F \frac{h}{\sin \alpha}.$ Find $\sin \alpha$ from the condition $F - mg \sin \alpha = ma$. The magnitude of $\sin \alpha$ is found from the condition $F - mg \sin \alpha = ma$.
22. A certain force pushes a body of mass $m = 16 \, \text{kg}$ up an inclined plane of length $l = 3.1 \, \text{m}$ and inclination $\alpha = 30^\circ$ to the horizon.
- The body's speed at the base of the plane was $v_0 = 0.6 , \text{m/s}$, and at the top edge, it was $v_1 = 3.1 , \text{m/s}$. What is the work done by the force? There is no friction.
- What is the work done by the same force, and what will be the kinetic energy of the body at the top of the inclined plane if there is friction with a coefficient $k = 0.1$? The force acts along the inclined plane.
Answer
1. $A = mgl \sin \alpha + \frac{m (v_1^2 - v_0^2)}{2} = 317$ J.
- The work will be the same, but the kinetic energy is less by the amount $kmgl \cos \alpha \approx 42.5$ J, and at the highest point it is equal to 34.4 J.
23. A truck of mass $M = 6 \cdot 10^3 \, \text{kg}$ drives onto a ferry tied to the shore with two ropes at a speed $v = 18 \, \text{km/h}$. After boarding, the truck stops, traveling a distance $s = 10 \, \text{m}$ while braking. Determine the total tension force in the ropes.
Answer
$F_{drag} = Mv^2/(2s) = 7500$ H.
24. A car moving at speed $v = 54 \, \text{km/h}$ brakes sharply and begins to skid (the locked wheels slide on the road). Determine the acceleration $a$ and the distance $s$ the car will travel if the sliding friction coefficient between the wheels and the asphalt is:
a) $k_1 = 0.3$ in wet weather;
b) $k_2 = 0.7$ in dry weather.
Answer
a) $a_1 \approx 2.94$ m/s², $s_1 \approx 38.3$ m;
b) $a_2 \approx 6.86$ m/s², $s_2 \approx 16.4$ m.
Hint
The kinetic energy of the car is spent on the work of overcoming friction: $mv^2/2 = kmgs$.
25. A car with fully engaged brakes (wheels locked) can remain stationary on a slope with an inclination of up to $23^\circ$. What is the braking distance $s$ of the car on a horizontal road when the initial speed is 10 m/s? The coefficient of friction between the wheels and the ground is the same on the slope and the road.
Answer
$s \approx 12$ m.
Hint
The coefficient of friction between the wheels and the ground is determined from the condition of immobility of the car at the critical angle of inclination of the mountain $\alpha$ and is equal to $\tan \alpha$.
26. A sled with a load of mass $M = 120 \, \text{kg}$ slides down a slope inclined at $\alpha = 14^\circ$ to the horizon. The length of the descent is $l = 60 \, \text{m}$. The sliding friction coefficient of the sled is $k = 0.14$. Determine:
a) the acceleration $a_1$ of the sled during the descent;
b) the speed $v$ at the end of the descent;
c) the time $t_1$ of the descent;
d) the kinetic energy $T_1$ at the end of the descent;
e) the distance $s$ the sled will travel horizontally after the descent;
f) the time $t_2$ of horizontal motion;
g) the acceleration $a_2$ during horizontal motion.
Answer
a) $a_1 = g (\sin \alpha - k \cos \alpha) = 1.04$ m/s²;
b) $v = \sqrt{2a_1 l} \approx 11.2$ m/s;
c) $t_1 = v/a_1 = \sqrt{2l/a_1} = 10.7$ s;
d) $T_1 = mgl (\sin \alpha - k \cos \alpha) \approx 7620$ J;
e) $s = \frac{l}{k} (\sin \alpha - k \cos \alpha) = 45.3$ m;
f) $t_2 = 2s/v \approx 8$ s; g) $a_2 = -kg = -0.14g$.
27. A body slides down an inclined plane. The angle of inclination is $\alpha = 20^\circ$, the length is $l = 4 \, \text{m}$, and the friction coefficient between the body and the plane is $k = 0.2$. What will be the speed $v$ of the body as it transitions from the inclined plane to the horizontal surface?
Answer
$v = \sqrt{2gl (\sin \alpha - k \cos \alpha)} \approx 3.4$ m/s.
28. A pool of area $S = 100 \, \text{m}^2$, filled with water to a depth $h = 1 \, \text{m}$, is divided in half by a vertical partition. The partition is slowly moved horizontally so that it divides the pool in a 1:3 ratio. What work must be done for this if no water leaks through the partition?
Answer
$A = \dfrac{1}{6} \rho g h^2 S = 1.63 \cdot 10^5$ J.
Hint
The work is equal to the difference in potential energies of the water before and after moving the partition.
29. Two cars start simultaneously from rest and accelerate uniformly. Their masses are equal. How many times greater is the average power of the first car's engine compared to the second if, in the same time, the first car reaches twice the speed of the second? Neglect resistance.
Answer
By 4 times.
Hint
Each of the cars acquires kinetic energy over time $t$, equal to $N_1 t$ and $N_2 t$ respectively, therefore $N_1 / N_2 = v_1^2 / v_2^2$.
30. An airplane needs a speed $v = 25 \, \text{m/s}$ for takeoff. The takeoff run is $s = 100 \, \text{m}$. What is the power of the engines if the airplane's mass is $m = 1000 \, \text{kg}$ and the resistance coefficient is $k = 0.02$? Assume the airplane's motion during takeoff is uniformly accelerated.
Answer
$N = mv \left( \dfrac{v^2}{2s} + kg \right) \approx 83.1$ kW.
Hint
The power of the motors during takeoff is $N = F_T v,$ where $F_T$ is the thrust force of the motors, which can be found by writing Newton's second law: $F_T - kmg = ma$ and substituting the acceleration of the aircraft during takeoff $a = v^2 / (2s)$.
31. A train of mass $M = 5 \cdot 10^5 \, \text{kg}$ climbs a slope of 10 m per kilometer at a speed of 30 km/h. The resistance coefficient is $k = 0.002$. Determine the power developed by the locomotive.
Answer
$N \approx 500$ kW.
32. After accelerating, an ice skater moves uniformly along a horizontal ice track for some time. Then, without pushing off, the skater travels a distance $s = 60 \, \text{m}$ in $t = 25 \, \text{s}$ before stopping. The skater's mass is $m = 50 \, \text{kg}$. Determine: a) the friction coefficient; b) the power expended by the skater during uniform motion.
Answer
a) $k = 2s/(gt^2) \approx 0.02$; b) $N = 4ms^2/t^3 \approx 46$ W.
33. A locomotive pulls a train with a total mass $m = 2000$ tonnes. Given that the locomotive's power $N$ is constant and equal to 1800 kW, and the resistance coefficient $k = 0.005$, determine:
a) the train's acceleration $a$ when its speed is $v_1 = 4 , \text{m/s}$ and when its speed is $v_2 = 12 , \text{m/s}$;
b) the maximum speed $v_{\text{max}}$ of the train.
Answer
a) $a = \frac{N}{mv} - kg$; $a_1 = 0.176$ m/s²; $a_2 = 0.026$ m/s²;
b) $v_{max} = N/(kmg) \approx 66$ km/h.
34. A pulley of radius $R$ rotates at $n$ revolutions per second, transmitting power $N$ via a belt. Find the tension force $T$ in the belt, assuming no slipping.
Answer
$T = N/(2\pi Rn)$.
Hint
The power transmitted by the belt is $N = Tv$, where $v = 2\pi Rn$ is the speed of the belt.
35. Find the power of an air stream with a circular cross-section of diameter $d = 18 \, \text{m}$, flowing at a speed $v = 12 \, \text{m/s}$. The air density (under normal conditions) is $\rho = 1.3 \, \text{kg/m}^3$.
Answer
$N \approx 284$ kW.
Hint
The power of the flow is equal to the work that the flow can perform in one second during the complete conversion of its kinetic energy into work: $N = \frac{mv^2/2}{t}$. Here $m$ is the mass of air passing through the cross-section $S$ of the flow in time $t$. Therefore $N = \frac{\pi \rho d^2 v^3}{8}$ (assuming \(a\) in OCR corresponds to diameter \(d\)), i.e., the power of the flow is proportional to the cube of its velocity.
36. A mountain stream with a cross-sectional area $S$ forms a waterfall of height $h$. The water flow speed is $v$. Find the power of the waterfall.
Answer
$N = \rho g S v h + \frac{\rho S v^3}{2}$.
Hint
See solution to problem 35. The speed of water at the base of the waterfall $v_1$ can be easily found from the energy conservation law: $m \frac{v^2}{2} + mgh = m \frac{v_1^2}{2}.$
37. A road section has a slope of 0.05. Descending with the engine off, a car moves uniformly at $v = 60 \, \text{km/h}$. What engine power is required for the car to ascend the same slope at the same speed? The car's mass is $m = 1.5$ tonnes.
Answer
$N = 2mgv \sin \alpha = 24.5$ kW, where $\sin \alpha = 0.05$.
Solution
The power of the car's engine must be equal to $N = F_T v$, where $F_T$ is the traction force. Since the car moves uniformly, $F_T$ is equal to the sum of the resistance force acting on the moving car and the component of gravity along the inclined plane: $F_T = F_{res} + mg \sin \alpha.$ For a car moving downhill, one can write, on the other hand: $mg \sin \alpha - F_{res} = 0,$ from which $F_{res} = mg \sin \alpha$, and $F_T = 2mg \sin \alpha$. Thus, $N = 2mgv \sin \alpha$.
38. Trucks equipped with engines of power $N_1$ and $N_2$ achieve speeds $v_1$ and $v_2$, respectively. What will be their speed if they are connected by a tow rope?
Answer
$v = \dfrac{(N_1 + N_2) v_1 v_2}{N_1 v_2 + N_2 v_1}$.
Hint
For trucks connected by a rope, $N_1 + N_2 = (F_1 + F_2) v$, where $F_1$ and $F_2$ are the traction forces of the trucks, equal to the resistance forces of the motion.
39. A snowmobile moves uphill on a gentle slope at a steady speed $v_1 = 20 \, \text{m/s}$. If it moves downhill at the same engine power, its speed becomes $v_2 = 30 \, \text{m/s}$. What speed $v$ will it achieve on a horizontal path with the same engine power?
Answer
$v \approx 2 \dfrac{v_1 v_2}{v_1 + v_2} \approx 24$ m/s.
Solution
When the aerosled moves uniformly upwards, the traction force is $F_1 = mg \sin \alpha + kmg \cos \alpha. \tag{1}$ When moving downwards $F_2 = kmg \cos \alpha - mg \sin \alpha, \tag{2}$ where $k$ is the coefficient of friction; $m$ is the mass of the aerosled. Since the engine power is constant, $N = F_1 v_1 = F_2 v_2. \tag{3}$ When moving on a horizontal path $N = kmgv$ (4). Adding equations (1) and (2) term by term, we get $F_1 + F_2 = 2kmg \cos \alpha. \tag{5}$ Solving equations (3), (4), and (5) together, we find $v = 2 \cos \alpha \times \frac{v_1 v_2}{v_1 + v_2}.$ Since the ascent is slight, i.e., $\alpha$ is small, then $\cos \alpha \approx 1$ and $v = 2 \frac{v_1 v_2}{v_1 + v_2}.$
40. A train of mass $m = 500$ tonnes moves uniformly on a horizontal track. The last car of mass $m_1 = 20$ tonnes detaches. After traveling $s = 240 \, \text{m}$, the driver shuts off the steam supply. How far apart will the detached car and the rest of the train come to rest? Assume the traction force is constant, and the resistance is proportional to the mass.
Answer
250 m.
Solution
Let the speed of the train at the moment the car detaches be $v$. By the time the car stops, its kinetic energy will be completely converted into work against friction: $m_1 v^2 / 2 = km_1 g s_1,$ where $s_1$ is the distance traveled by the car until it stops. During uniform motion of the train, the traction force is balanced by the total resistance force: $F_T = kmg.$ When the rear car detached, the resistance force decreased, but the traction force, according to the problem statement, did not change. A net force $F$ started acting on the train, accelerating its motion: $F = kmg - k(m - m_1)g = km_1 g.$ After the car detached, the train began to move under the action of this force with acceleration, and its kinetic energy over the path $s$ increased by an amount $\Delta T$, equal to the work of the force $F$ over the path $s$: $\Delta T = km_1 g s.$ Before the detachment, the kinetic energy of this part of the train was $(m - m_1)/m$ times the energy of the car, i.e., it was equal to $k(m - m_1)gs_1$. Therefore, by the time the steam supply stopped, the train had kinetic energy $T = k(m - m_1)gs_1 + km_1 g s.$ This energy is spent on the work of overcoming the resistance of the train's motion over the path $s_2$: $k(m - m_1)gs_1 + km_1 g s = k(m - m_1)gs_2.$ From this equation, we find $s_2 - s_1 = m_1 s / (m - m_1)$, and the distance between the stopped train and the car is $x = s_2 - s_1 + s = \frac{ms}{m - m_1}.$ Another solution is in problem 50 in Chapter: Newton's Laws.
41. Find the work required to drag a body of mass $m = 50 \, \text{kg}$ up a hill of arbitrary profile along a flat trajectory from point $A$ to point $B$, where the horizontal distance is $l = 10 \, \text{m}$ and the vertical height is $h = 10 \, \text{m}$. The friction coefficient between the body and the hill is $k = 0.1$. The hill's profile is such that the tangent at any point forms an acute angle with the horizon. The applied force always acts tangentially to the path.
Answer
$A = mg(kl + h) \approx 5500$ J.
Solution
Let's divide the entire path into small straight sections. Then the work on each section is $\Delta A = kmg \Delta l \cos \alpha + mg \Delta l \sin \alpha$, where the first term is the work against the friction force, and the second is the part of the work that goes into increasing the potential energy of the body. Noting that $\Delta l \cos \alpha$ and $\Delta l \sin \alpha$ are the projections of the path segment onto the horizontal and vertical directions, respectively, we find that the total work will be equal to $A = kmgl + mgh = mg(kl + h)$.