1. Two train cars—one loaded, one empty—roll down a sorting hill. Which will travel farther on the straight track after descending? Assume the drag force is proportional to the load on the wheels and independent of speed. Neglect air resistance.
Answer
Both wagons will travel the same distance.
2. What mass of ballast $m$ must be dropped from a uniformly descending balloon to make it ascend uniformly at the same speed? The balloon's total mass is $M = 1200\, \text{kg}$, its lift force is constant at $F = 8000\, \text{N}$, and drag is the same for ascent and descent.
Answer
$m = 2(\frac{F}{a} - M) \approx 800$ kg.
Hint
The conditions for uniform motion of the aerostat during descent and ascent are expressed respectively: $Mg = F + F_{\text{res}}$; $(M-m)g + F_{\text{res}} = F$.
3. A mine cage of mass $M = 3 \cdot 10^3\, \text{kg}$ starts ascending at $a = 0.49\, \text{m/s}^2$. Find:
a) the cable tension;
b) the tension when descending at the same acceleration;
c) the tension when moving up or down at constant speed.
Answer
a) $F_N = M(g+a) \approx 3.1 \times 10^4$ H;
b) $F_N = M(g-a) \approx 2.8 \times 10^4$ H;
c) $F_N = Mg \approx 2.95 \times 10^4$ H.
4. A person stands on a spring scale in an elevator. How do the scale readings change as the elevator moves up and down, considering changes in motion?
Answer
When the elevator moves with acceleration directed upwards (this will be at the beginning of the ascent and at the end of the descent), the scale reading is greater than $mg$ ($m$ is the mass of the person). If the acceleration is directed downwards, which will be at the beginning of the descent and at the end of the ascent, the scale reading is less than $mg$. If the elevator moves uniformly, the scale reading is equal to $Mg$.
Hint
The equation of motion for the person is $ma = mg - N$ (equation written in projections onto the direction of $g$). Here $a$ is the acceleration of the elevator (algebraic quantity) and $N$ is the reaction force of the scales. In accordance with Newton's third law, the force $N'$ acting on the scales from the person is equal in magnitude to $N$: $N' = N = m(g-a)$.
5. A person stands on a board and suddenly crouches. Does the board's deflection initially increase or decrease? What happens if the person was squatting and suddenly stands?
Answer
When squatting, it will decrease; when straightening up, it will increase.
Hint
When squatting, the acceleration of the person's center of mass is directed downwards, and when straightening up - upwards.
6. A box filled with balls is thrown upward. How do the forces of the balls on the box's bottom, sides, and each other change during flight? How does the answer change if the box is thrown at an angle? Neglect air resistance.
Answer
During the free movement of the box (movement in the field of gravity in the absence of other forces), the pressure force of the balls on the bottom and walls of the box, as well as on each other, is zero.
7. A heavy object is suspended from a spring attached to an elevator ceiling. How will the object move relative to the elevator if the elevator starts free-falling?
Answer
The body will oscillate on the spring, the amplitude of which is equal to the initial extension of the spring.
Hint
The problem is conveniently solved in a non-inertial coordinate system associated with the moving elevator (see 'Elementary Physics Textbook' edited by Acad. G. S. Landsberg, vol. I, ch. 6). In this reference frame, three forces act on the mass: the force of gravity $mg$, the inertial force $-ma$ balancing it, and also the spring tension force, equal at the initial moment to the force of gravity $mg$ acting on the mass.
8. A body on a stand is suspended from a ceiling by a spring (initially unstretched). The stand is lowered at acceleration $a$. After what time $\Delta t$ will the body lift off? The spring constant is $k$, and the body's mass is $m$.
Answer
$\Delta t = \sqrt{2m(g-a)/(ka)}$.
Solution
Until the moment the body detaches from the support, it moves with acceleration $a$ under the action of three forces: the force of gravity $F_1 = mg$, the spring tension force $F_2 = kx$, and the support reaction force $N$. Therefore $mg - kx - N = ma$. At the moment the body detaches from the support, the support reaction force becomes zero. Considering this and substituting the expression for $x = a(\Delta t)^2/2$ into the equation of motion, we find $\Delta t = \sqrt{2m(g-a)/(ka)}$.
9. Masses $m_1 = 50\, \text{g}$ and $m_2 = 75\, \text{g}$ are hung from a cord over a pulley. Neglecting friction, cord and pulley mass, and cord stretch, find the accelerations, cord tension, and dynamometer reading supporting the pulley.
Answer
$a \approx 1.96$ m/s$^2$; $T \approx 0.6$ H; $F \approx 1.2$ H.
Solution
The forces acting on the weights are shown in the following figure. Let's write the equations of motion for the weights: $m_1 a_1 = m_1 g - T_1,\tag{1}$ $m_2 a_2 = T_2 - m_2 g. \tag{2}$ The accelerations $a_1$ and $a_2$ of the weights are numerically equal, since the string is inextensible and the displacements of the weights are always the same (the relationships between the accelerations of the bodies of the system are determined by their kinematic connection, i.e., the connection between their displacements). In the general case, the forces $T_1$ and $T_2$ applied to the ends of the string, according to Newton's third law, are numerically equal to the forces $T'_1$ and $T'_2$, are not equal to each other, i.e., the difference between these forces imparts acceleration to the string and angular acceleration to the pulley. If the mass of the string and pulley can be neglected, then $T_1$ and $T_2$ and the corresponding forces $T'_1$ and $T'_2$ applied to the weights can be considered equal to each other. Projecting the vectors included in equations (1) and (2) onto the directions $x_1$ and $x_2$, coinciding with the accelerations of each of the weights (conventionally assume $m_1 > m_2$), we obtain the following system of equations: $m_1 a = m_1 g - T$; $m_2 a = T - m_2 g$. Solving this system for the unknowns $a$ and $T$, we get $a = \frac{m_1 - m_2}{m_1 + m_2} g$; $T = \frac{2m_1 m_2}{m_1 + m_2} g$. (If $m_1 < m_2$, we get $a < 0$, i.e., the weights move in the direction opposite to the assumed one.) The dynamometer reading is obviously equal to the sum of the string tension forces: $F = 2T = \frac{4m_1 m_2}{m_1 + m_2} g.$ 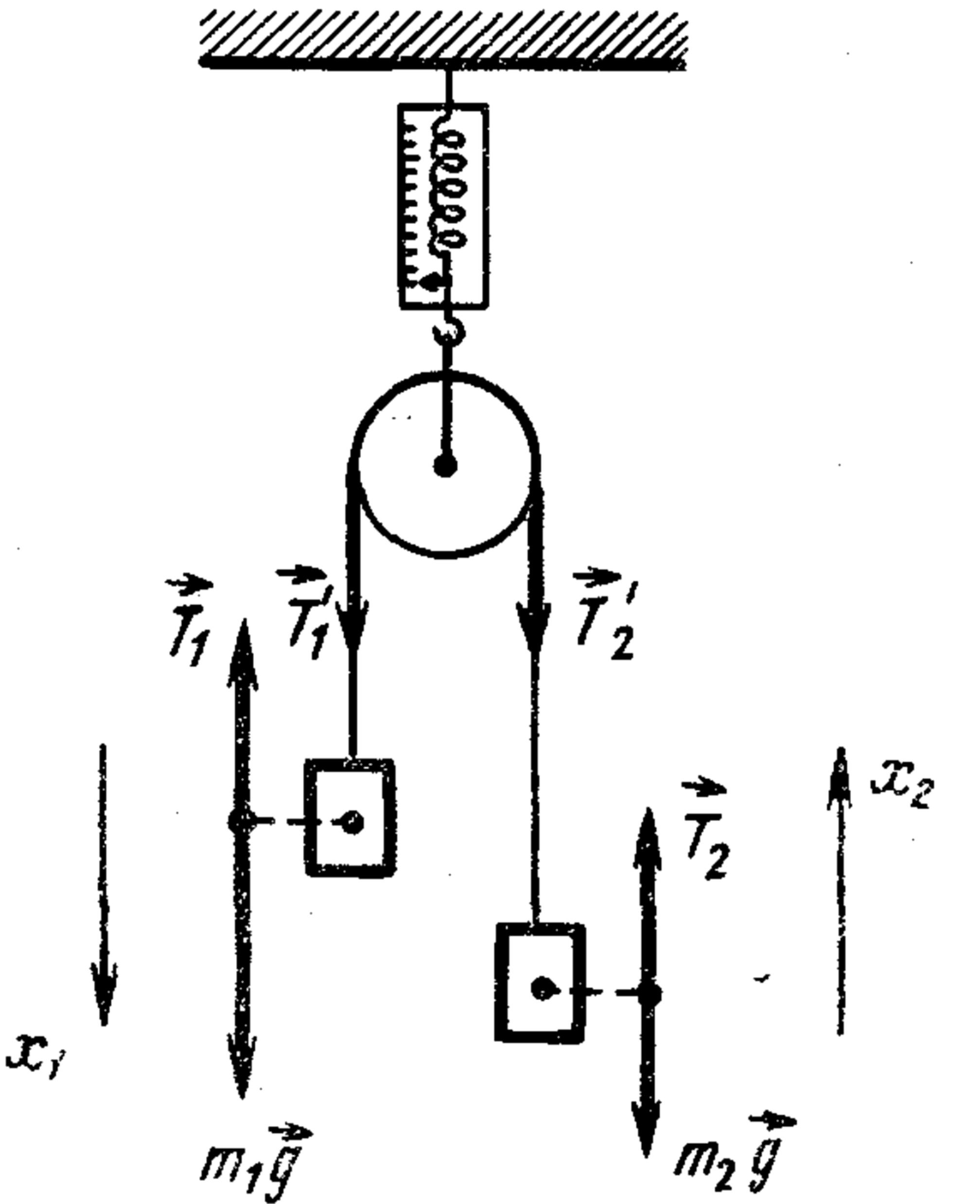
10. Two masses $m_1 = 7\, \text{kg}$ and $m_2 = 11\, \text{kg}$ hang from a cord over a pulley. Initially at the same height, how long $t$ until the lighter mass is 10 cm above the heavier one? Neglect pulley and cord mass and friction.
Answer
$t = 0.21$ s.
Hint
See the previous problem. Each weight will travel a path equal to 5 cm.
11. Two identical masses $M$ are hung from a cord over a pulley. A small mass $m$ is placed on one. Find the force $f$ of $m$ on $M$ and the force $F$ on the pulley's axle.
Answer
$F = 4Mg (\dfrac{m+M}{m+2M})$; $f = 2 \dfrac{Mm}{m+2M} g$.
Solution
In accordance with Newton's second law, let's write the equations of motion for each of the bodies (see figure): for the first body $Ma = T - Mg;$ for the second body $Ma = Mg + f - T;$ for the load $ma = mg - f',$ where $T$ is the string tension force; $f$ is the pressure force of the load on the body, $a$ is the acceleration of the bodies; $f'$ is the reaction force of the support. According to Newton's third law, $f'$ and $f$, $T$ and $T'$ are numerically equal. The tensions on the right and left are equal, since friction and the mass of the pulley are neglected. Solving the obtained system of equations, we find $a = \frac{mg}{m+2M};$ $f = 2 \frac{Mm}{m+2M} g,$ $T = M(\frac{mg}{m+2M} + g) = 2M (\frac{m+M}{m+2M}) g.$ The force acting on the axis of the pulley, $F = 2T = 4M (\frac{m+M}{m+2M}) g.$ 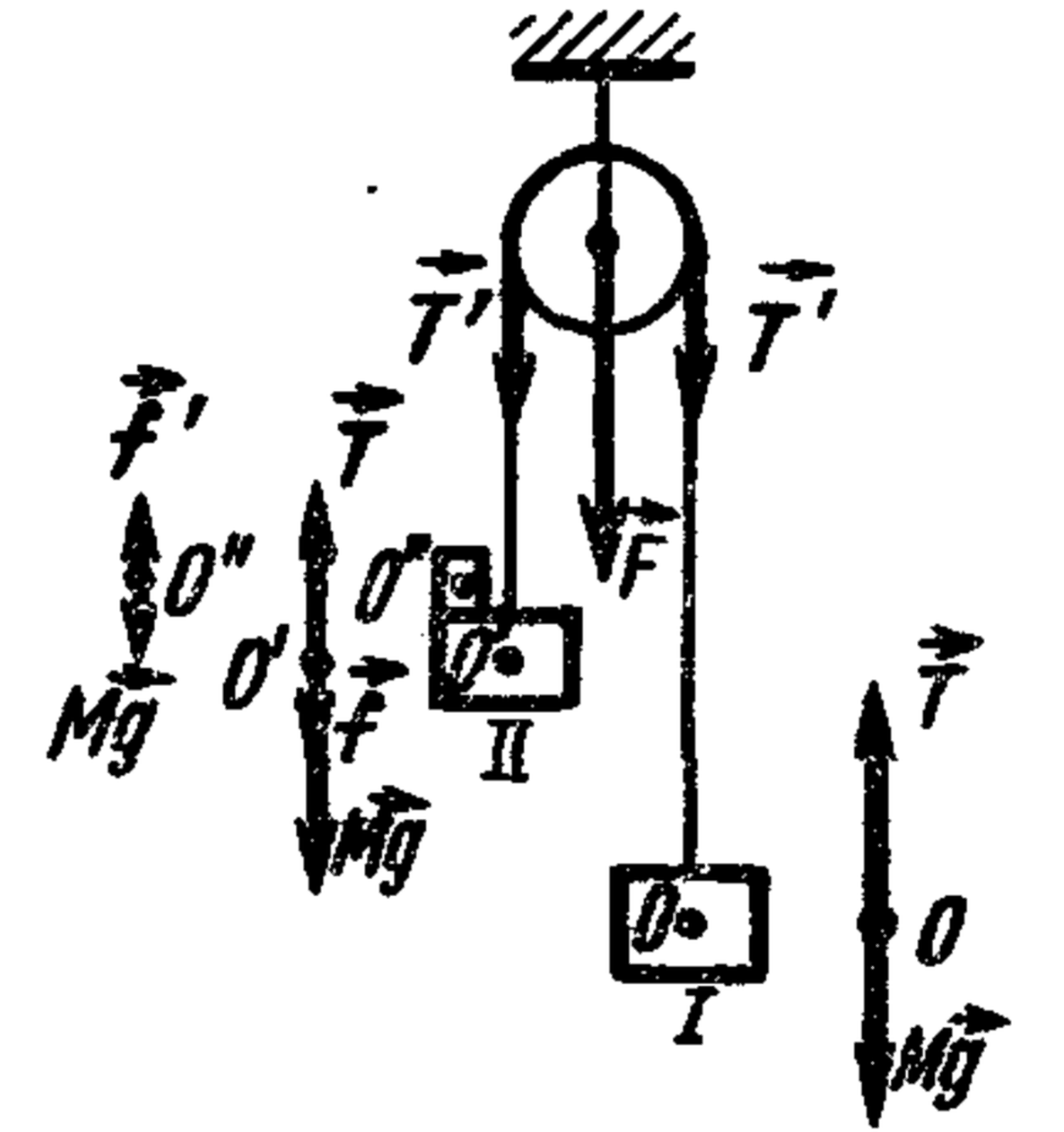
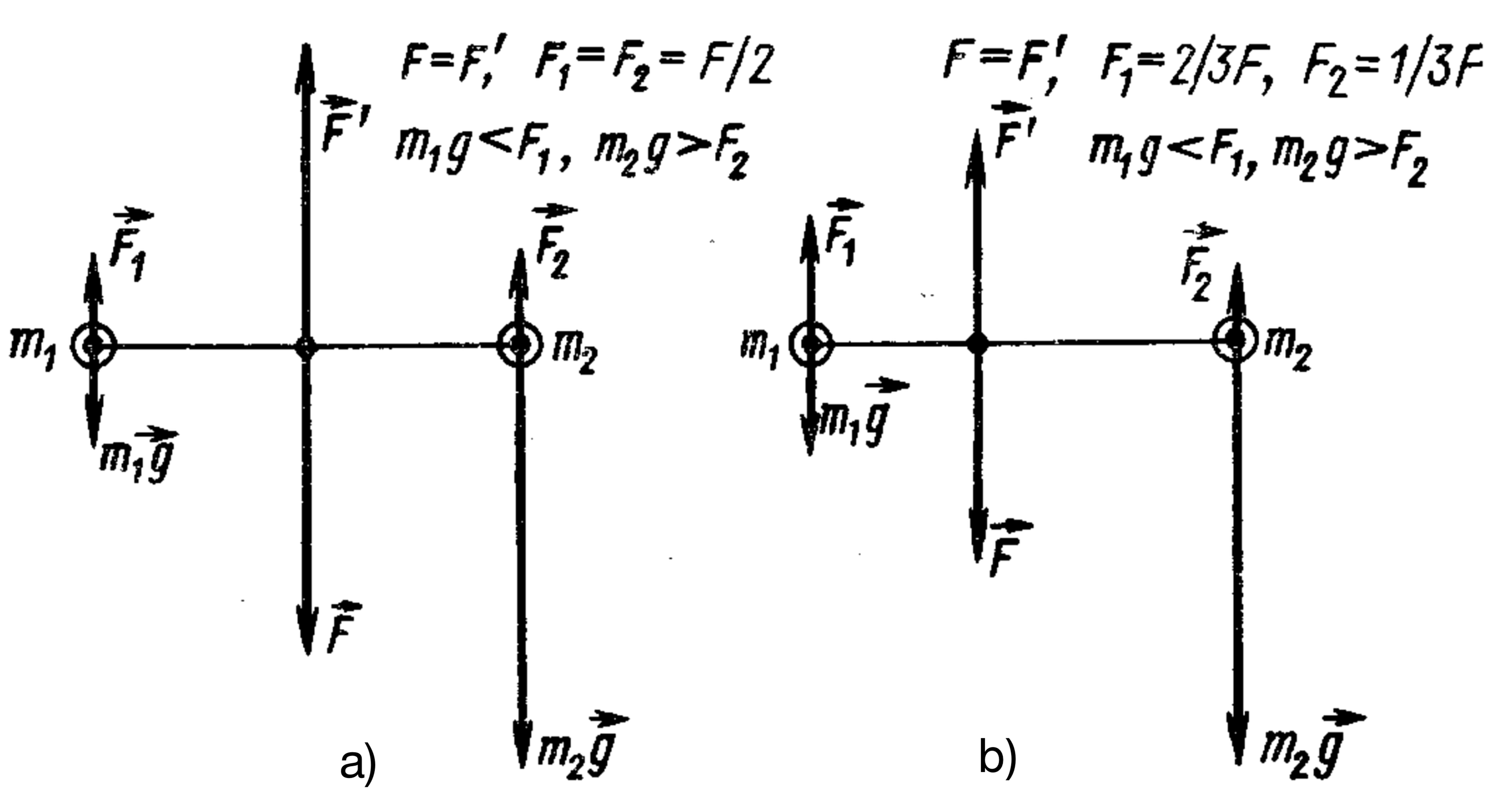
12. A horizontal axis passes through the middle of a rod, about which it can rotate. Masses with $m_1 = 2\,\text{kg}$ and $m_2 = 8\,\text{kg}$ are attached to the ends of the rod. The rod is brought to a horizontal position and released without a push.
- Find the force exerted by the rod on the axis at the initial moment after its release. Neglect the mass of the rod and friction at the axis; consider the masses as material points.
- Solve the problem for the case when the axis does not pass through the center of the rod but is located at a distance of $1/3$ of its length from the smaller mass.
Answer
1. $F = \dfrac{4m_1 m_2}{m_1 + m_2} g \approx 64$ N.
- $F = \frac{9m_1 m_2}{4m_1 + m_2} g \approx 42.3$ N.
Solution
1. The force $F'$, acting from the axis on the rod and according to Newton's third law numerically equal to the pressure force $F$ on the axis (see figure below, a), can be replaced by two forces $F_1$ and $F_2$, applied to each of the weights and equal to $F/2$. Considering that the rod is massless, we can, using Newton's second law, write: $m_1 a = F/2 - m_1 g$, $m_2 a = m_2 g - F/2$, whence $F = \frac{4m_1 m_2}{m_1 + m_2} g$.
- The force $F'$ must be replaced (see figure below, b) by forces $F_1 = (2/3)F'$ and $F_2 = (1/3)F'$, applied to weights $m_1$ and $m_2$ respectively. The accelerations of the weights are related by $a_1/l_1 = a_2/l_2$, i.e., $a_1 = a_2/2$.
13. Masses $m_1$ and $m_2$ hang from a cord over a pulley on a prism with angles $\alpha$ and $\beta$ (see figure). Find their accelerations and cord tension. Neglect friction. 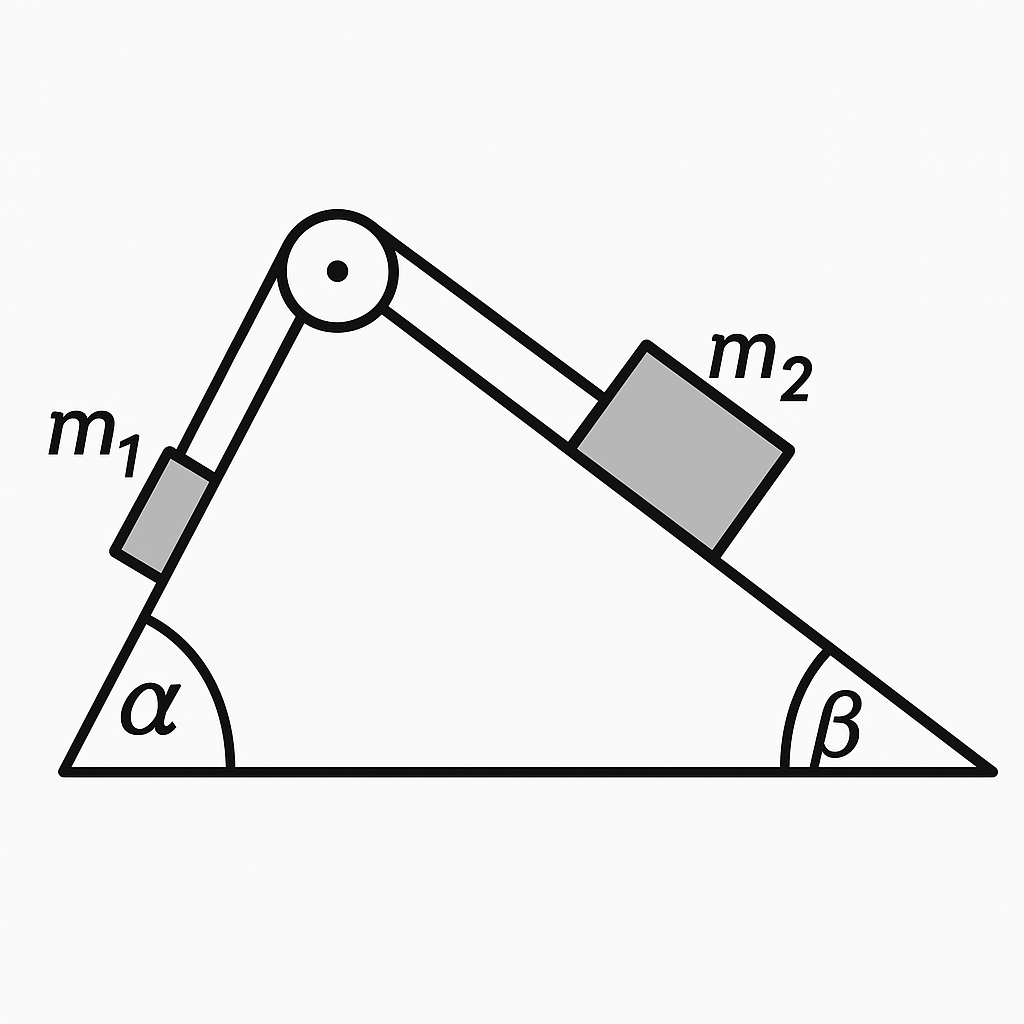
Answer
$a = \dfrac{m_1 \sin \alpha - m_2 \sin \beta}{m_1 + m_2} g$; $T = \dfrac{m_1 m_2 g (\sin \alpha + \sin \beta)}{m_1 + m_2}$.
Solution
Let's write the equations of Newton's second law for each of the weights, projecting the forces acting on the weights (see figure) onto the direction of possible motion of the corresponding weights, i.e., along the faces of the prism (assume that weight $m_1$ descends): $m_1 a = m_1 g \sin \alpha - T,$ $m_2 a = T - m_2 g \sin \beta.$ Solving this system, we find: $a = \frac{m_1 \sin \alpha - m_2 \sin \beta}{m_1 + m_2} g;$ $T = \frac{m_1 m_2 (\sin \alpha + \sin \beta)}{m_1 + m_2} g.$ If, upon substitution of the numerical values of masses and angles, it turns out that $a < 0$, it means that the entire system moves with acceleration $a$ in the direction opposite to the chosen one. The latter follows from the fact that in the absence of friction, changing the chosen direction of motion of the weights will only change the signs of the right sides of the equations derived above. 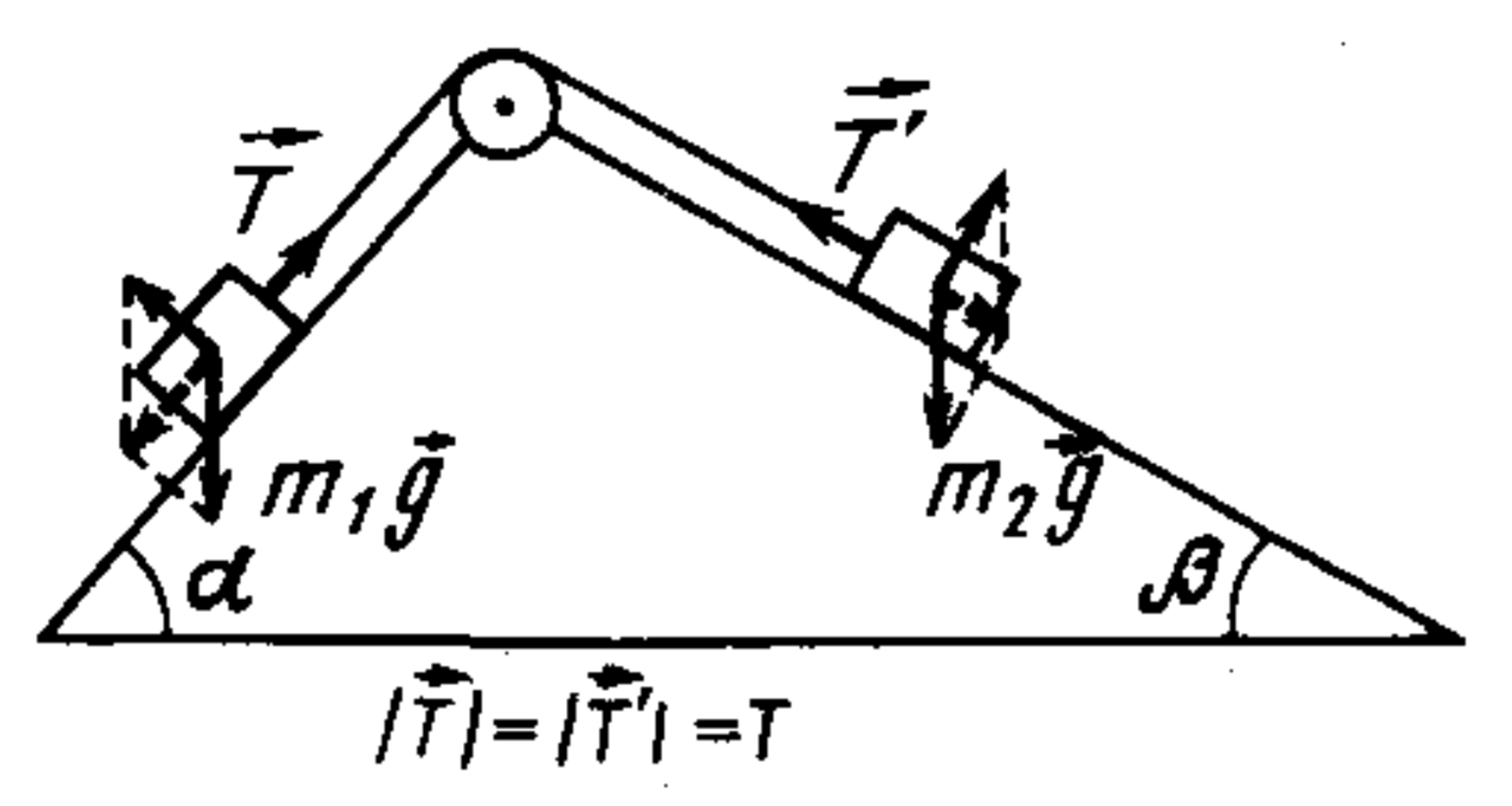
14. Two masses $m = 0.2 \, \text{kg}$ and $M = 4 \, \text{kg}$ are connected by a string and lie on a smooth table (friction is neglected). A force $F_1 = 0.2 \, \text{N}$ is applied to the first mass along the direction of the string, and a force $F_2 = 0.5 \, \text{N}$ is applied to the second mass in the opposite direction. With what acceleration $a$ will the masses move, and what is the tension force $T$ in the connecting string? Solve the problem in general form and draw a conclusion about the tension force in the string when $m \ll M$.
Answer
$a = 0.12$ m/s$^2$; $T = 0.22$ H; $T = \dfrac{F_1 M + F_2 m}{M+m} \approx \dfrac{F_1 + F_2 \frac{m}{M}}{1 + \frac{m}{M}} \approx F_1$, when $m \ll M$.
15. Find the accelerations $a_1$ and $a_2$ of masses $m_1$ and $m_2$ and cord tension $T$ in the system shown below. Neglect pulley and cord mass and friction. 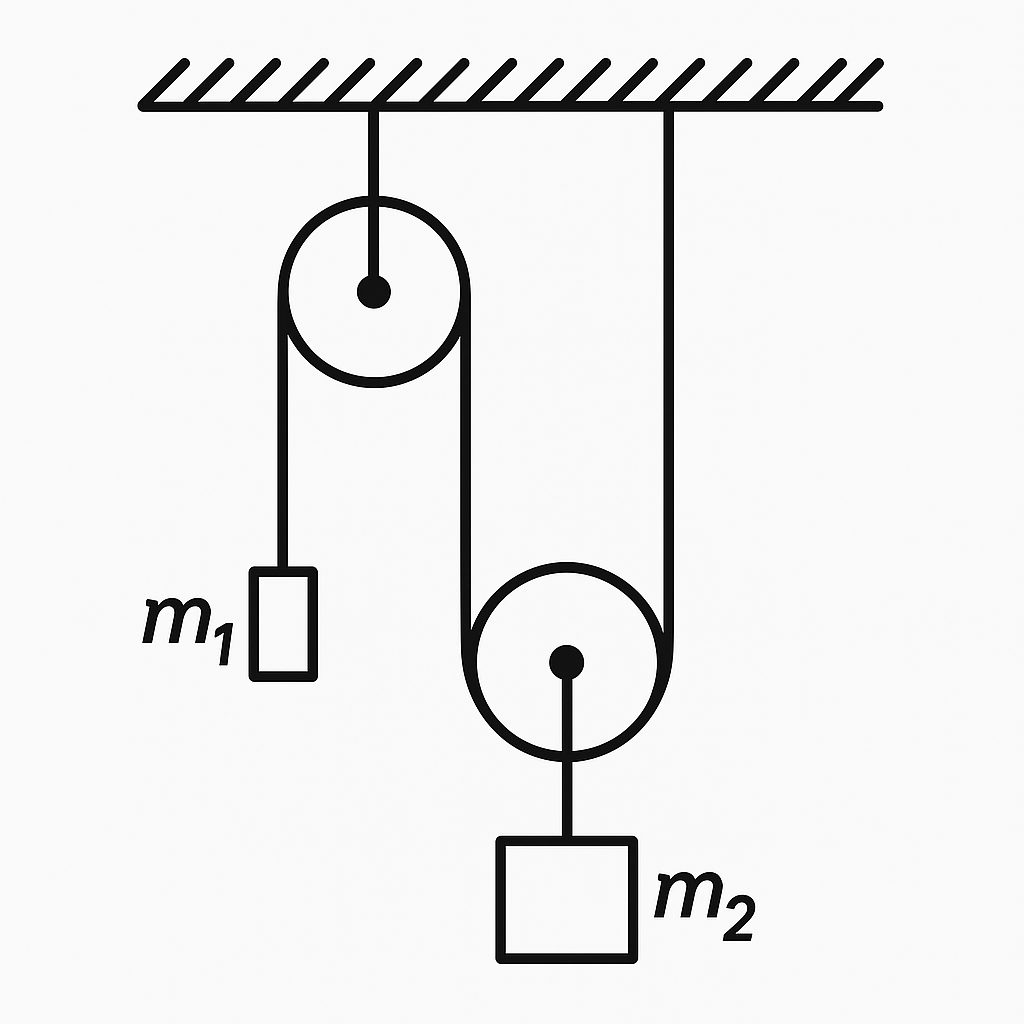
Answer
$a_1 = 2 \dfrac{2m_1 - m_2}{4m_1 + m_2} g$; $a_2 = \dfrac{2m_1 - m_2}{4m_1 + m_2} g$; $T = \dfrac{3m_1 m_2}{4m_1 + m_2} g$.
Hint
From the kinematic connection, it follows that the acceleration of weight $m_1$ is twice the acceleration of weight $m_2$ (when weight $m_1$ moves by distance $h$, weight $m_2$ moves by distance $h/2$). A force equal to $2T$ is applied to weight $m_2$ from the strings.
16. A cart with a liquid container moves horizontally at acceleration $a$. Find the angle of the liquid's surface to the horizon in steady state.
Answer
$\alpha = \arctan(a/g)$.
Solution
Let's conditionally isolate a small part of the liquid inside. Two forces act on this element of liquid with mass $m$: the force of gravity $mg$ and the buoyant (Archimedean) force $N$ from the side of the liquid. The resultant $F$ of these forces must be directed towards the acceleration of the vessel and equal to $ma$ (see figure). Therefore, the force $N$ must form an angle $\alpha = \arctan(a/g)$ with the vertical. The direction of the buoyant force $N$ acting on any isolated volume inside the liquid is perpendicular to the planes of equal pressure ($p$=const) in the liquid, is determined by them and, in particular, is perpendicular to its surface ($p=0$). The requirement of perpendicularity uniquely relates to the condition of rest of the liquid relative to the vessel. Any violation of perpendicularity is 'automatically' eliminated due to the fluidity of the liquid. 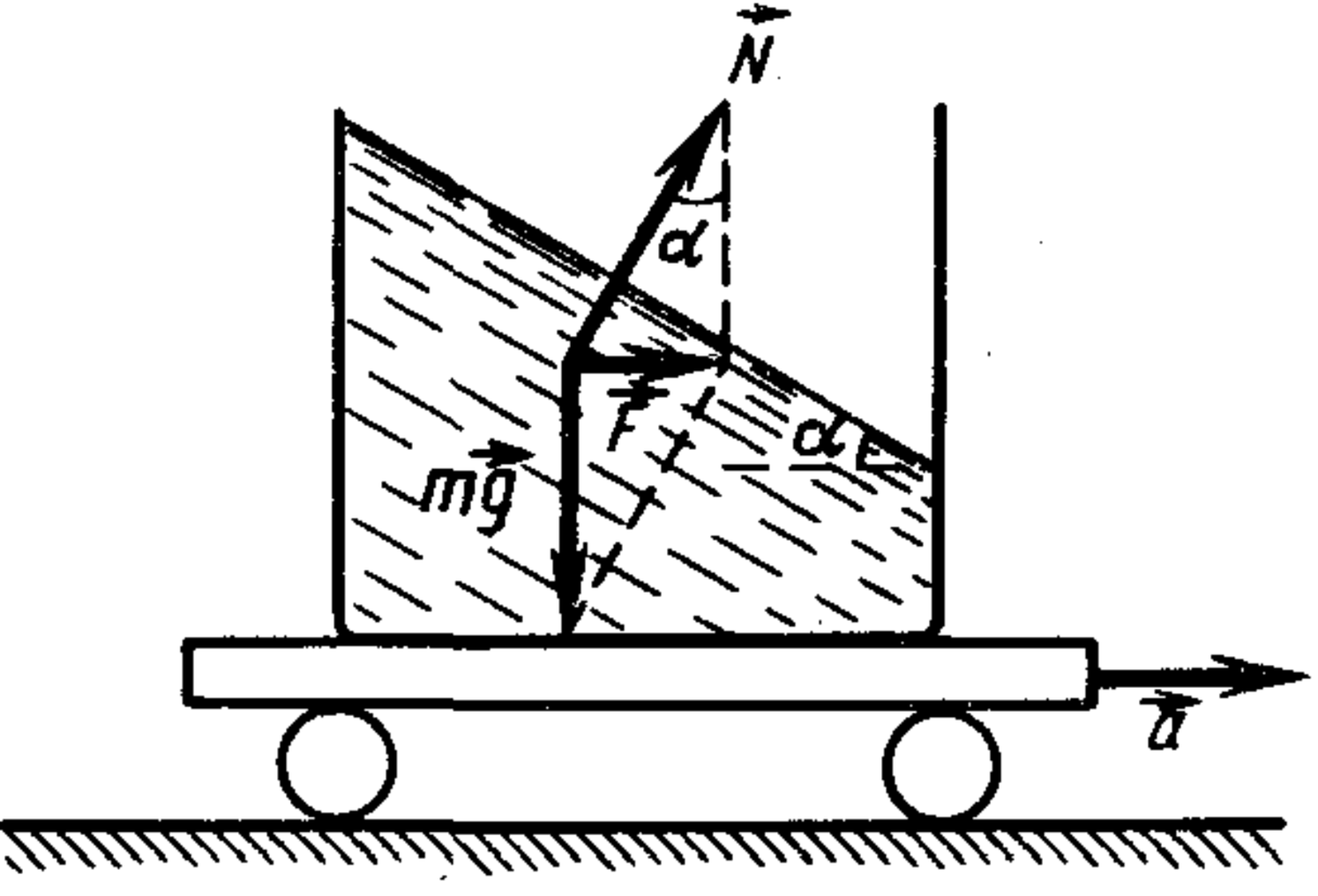
17. Find the angle of a liquid's surface in a container sliding without friction on an inclined plane.
Answer
The surface of the liquid is parallel to the inclined plane.
1st method. See solution to problem 16.
2nd method. Let's solve the problem in the reference frame associated with the moving vessel (in a non-inertial system). In this case, forces $mg$, $N$, and the inertial force $|-m\vec{a}| = ma$ act on any element of the liquid, directed opposite to the motion of the vessel (see figure). The resultafignt of these forces must be zero (since the liquid is stationary relative to the vessel). This is possible when the force $N$ is perpendicular to the inclined plane. The surface of the liquid is parallel to it.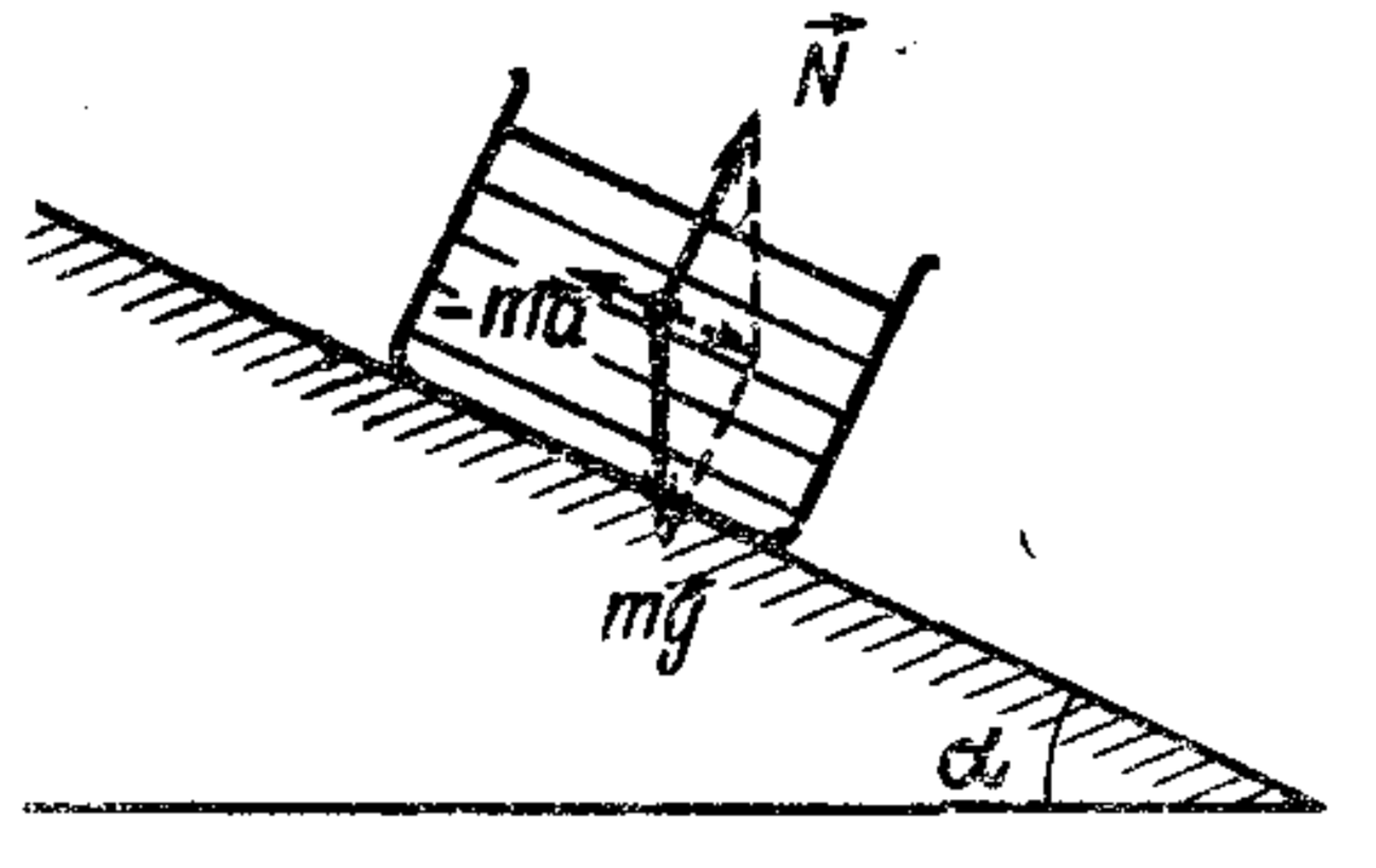
18. A bucket of water with a floating body is in an elevator. Does the body's submersion depth change if the elevator accelerates upward or downward?
Answer
Will not change.
Solution
When the elevator moves with acceleration $\vec{a}$, Newton's second law for a floating body is written as: $m\vec{a} = m\vec{g} + \vec{F},\tag{1}$ where $\vec{F}$ is the buoyant force; $m$ is the mass of the body.
If the volume displaced by the body were occupied by liquid, a force, also equal to $\vec{F}$, would act on it from the rest of the liquid. According to Newton's second law
$m_l \vec{a} = m_l \vec{g} + \vec{F}; \tag{2}$
here $m_l = \rho_l V$, where $V$ is the volume of the submerged part of the body. Substituting the expression for $\vec{F}$ found from equality (1) into equation (2), we get
$m(\vec{a} - \vec{g}) = \rho_l V (\vec{a} - \vec{g}),$
hence it follows that $V = m/\rho_l$ does not depend on the acceleration of the elevator, i.e., the immersion depth of the body does not change. Note. The solution to the problem becomes very simple in the reference frame associated with the elevator (see problem 17).
19. A board of mass $M$ can slide without friction on an incline at angle $\alpha$. A dog of mass $m$ runs on the board. What direction and acceleration must the dog have to prevent the board from sliding? What minimum friction coefficient $k$ between the dog and board is needed?
Answer
$a = g \sin \alpha (1 + M/m)$; $k > (M/m) \tan \alpha$.
Solution
The dog must run with such acceleration, directed downwards, so that the force $-F_1$, with which the dog pushes the board back, balances the resultant $F_1$ of the forces acting on the board: gravity $Mg$ and reaction force $N_1$, i.e., equals $Mg \sin \alpha$ (see figure). On the dog, therefore, in the direction of its acceleration, act the force $mg \sin \alpha$ and the force $F_1$ from the board, equal, according to Newton's third law, to $Mg \sin \alpha$ (the direction of the dog's movement does not matter). The equation of motion for the dog will be $ma = mg \sin \alpha + Mg \sin \alpha$, whence $a = g \sin \alpha (1 + M/m)$. The force $-F_1$, with which the dog pushes the board, by its nature, is a friction force, which cannot exceed the value $kN$. The problem has a solution (the dog stops the board) if $kN \ge F_1$, i.e., $kmg \cos \alpha \ge Mg \sin \alpha$. Hence $k \ge (M/m) \tan \alpha$.
1st method. See solution to problem 16.
2nd method. Let's solve the problem in the reference frame associated with the moving vessel (in a non-inertial system). In this case, forces $mg$, $N$, and the inertial force $|-m\vec{a}| = ma$ act on any element of the liquid, directed opposite to the motion of the vessel (see figure). The resultafignt of these forces must be zero (since the liquid is stationary relative to the vessel). This is possible when the force $N$ is perpendicular to the inclined plane. The surface of the liquid is parallel to it.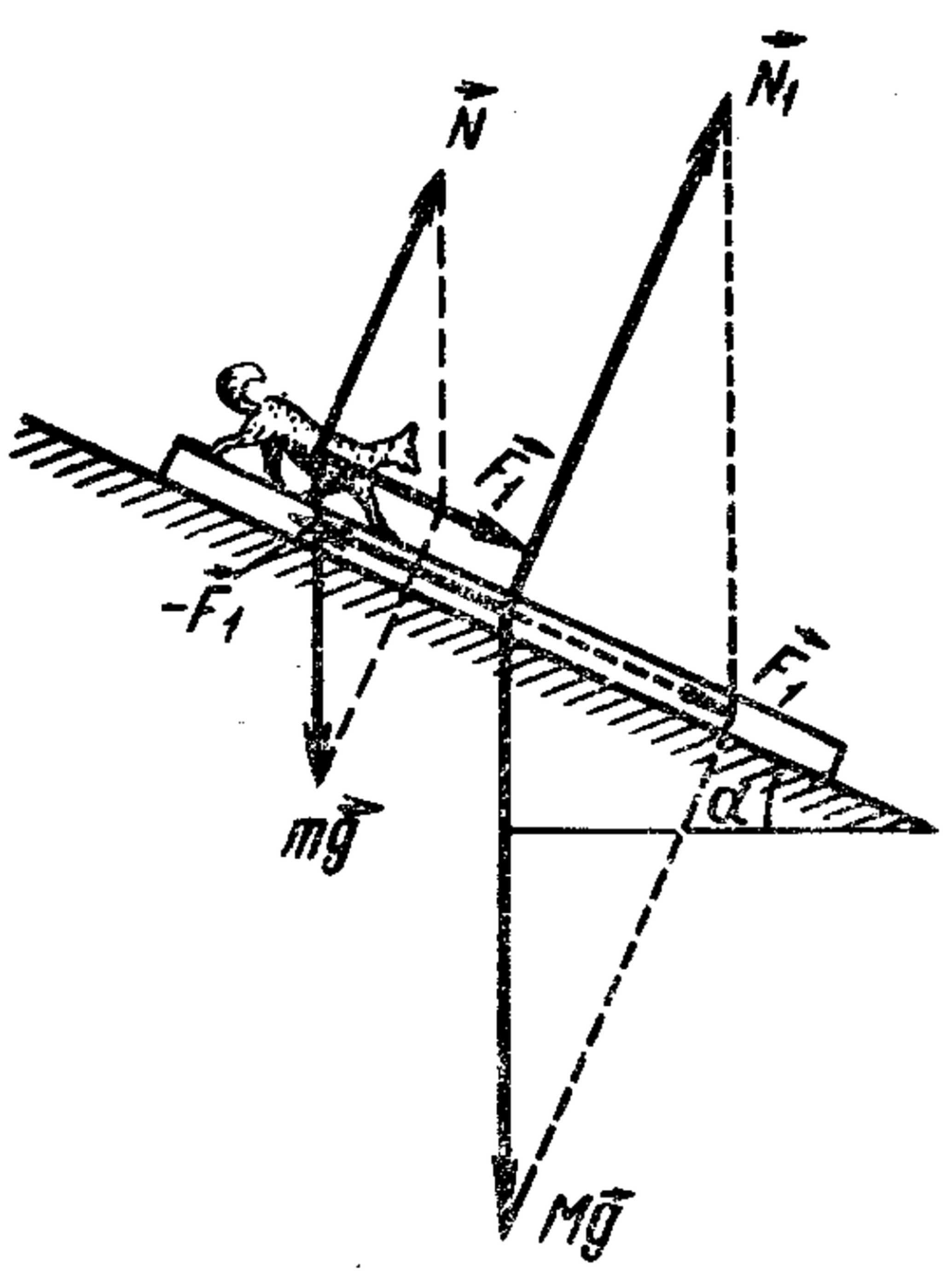
20. A cylinder of mass $M$ has a wound thread. When released, the thread is pulled upward so the cylinder's center remains at the same height. Find the thread's tension.
Answer
$Mg$.
Hint
The cylinder is at rest relative to the Earth.
21. A rope over a fixed pulley has a mass $m_1 = 64\, \text{kg}$ on one end and a person $m_2 = 65\, \text{kg}$ on the other. The person pulls the rope to lift the mass while staying at the same height. How long $t$ until the mass is raised $h = 3\, \text{m}$? Neglect rope and pulley mass.
Answer
$t \approx 6.26$ s.
Solution
Since the person is stationary relative to the Earth, the forces applied to him are balanced. Thus, the tension force is numerically equal to the weight of the person $m_2 g$. Therefore, for the weight, Newton's second law will be written as: $m_1 a = m_2 g - m_1 g = (m_2 - m_1)g$. Hence the acceleration of the weight $a = g \frac{m_2 - m_1}{m_1}$ and is directed upwards. The time for the weight to rise is determined from the formula $h = at^2/2$: $t = \sqrt{2h/a} = \sqrt{\frac{2hm_1}{g(m_2 - m_1)}}.$
22. 1. Two boys of equal mass on skates $l$ apart pull a rope: one at speed $v$, the other at $2v$. When and where will they meet? Solve also for mass ratio 1:1.5.
- Two gymnasts of equal mass pull a rope over a pulley and begin ascend simultaneously: one at speed $v$, the other at $2v$ relative to the rope. How long until each reaches the pulley? The rope's length is $l$, initially centered.
Answer
1. Both boys will reach the middle of the distance between them simultaneously after time $\tau = l/(3v)$; if the masses of the boys are unequal, the meeting place divides the distance between them inversely proportional to the masses of the boys.
- The gymnasts will reach the block simultaneously after time $\tau = l/(3v)$.
Solution
Since the forces applied to the boys are equal, according to Newton's third law, the accelerations, and consequently, the velocities of the boys relative to the Earth are equal. The length of the rope between the boys decreases with speed $3v$ and the boys will reach the middle of the distance between them after time $\tau = l/(3v)$. If the masses of the boys are different, the accelerations and paths traveled by them relative to the Earth are inversely proportional to the masses of the boys.
- Compare the solution of this problem with the solution of problem item 1.
23. A body of mass $m = 1\, \text{kg}$ on a horizontal plane with friction coefficient $k = 0.1$ is acted on by force $F$. Find the friction force for $F = 0.5\, \text{N}$ and $F = 2\, \text{N}$.
Answer
0.5 N; 1 N.
Hint
The magnitude of the static friction force cannot exceed $F_{fr.max} = kN$, where $N$ is the normal pressure. If the body is at rest, the friction force is equal in magnitude to the sum of the projections of all forces acting on the body onto the direction of possible motion (i.e., onto the direction in which the body would start moving if the friction force were zero). If the force acting on the body in the direction of possible motion exceeds $F_{fr.max}$, the body moves with acceleration, and the friction force is constant and equal to $F_{fr.max}$.
24. A block of mass $m = 2\, \text{kg}$ on a horizontal surface has sliding friction coefficient $k = 0.2$. Plot the friction force versus applied pulling force. Neglect static friction.
Answer
The graph is shown below. 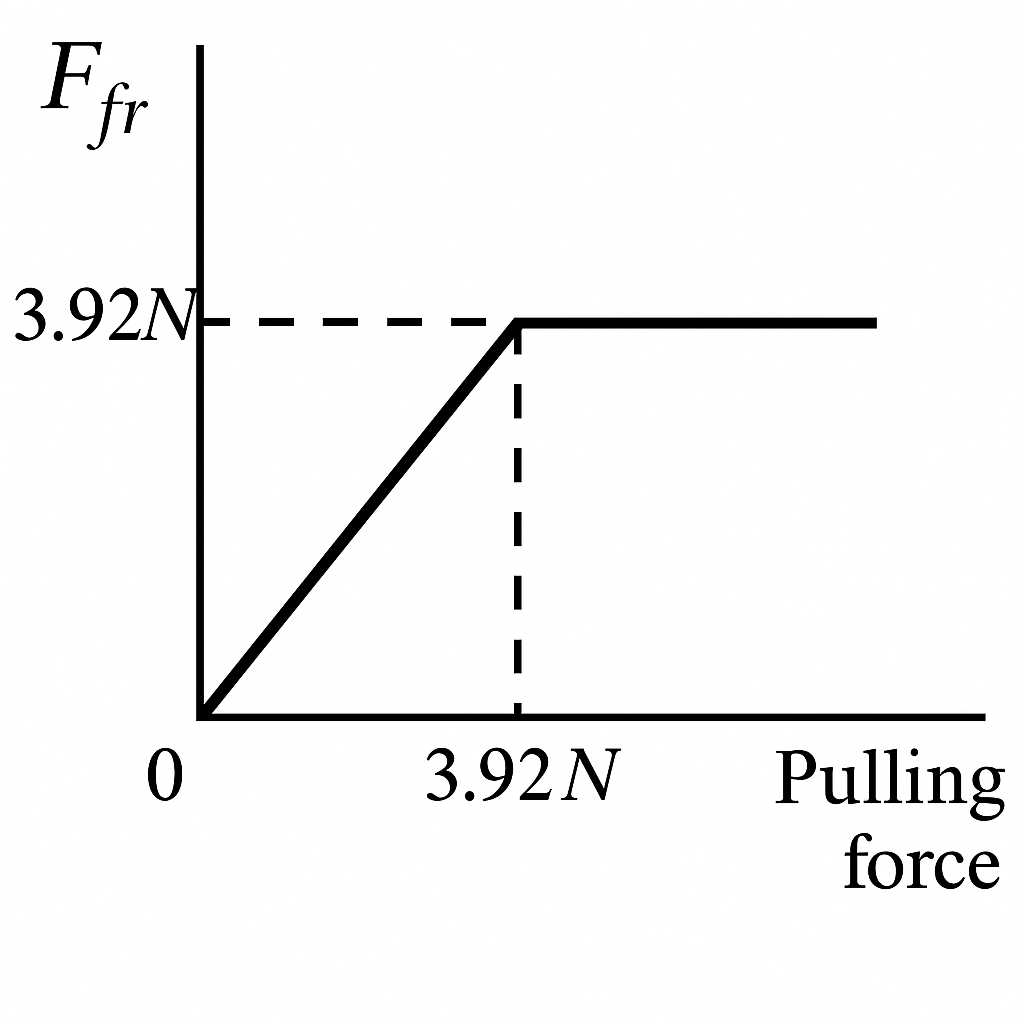
25. A block is on a plane whose angle $\alpha$ can vary from $0^\circ$ to $90^\circ$. Plot the friction force versus $\alpha$. Neglect static friction.
Answer
The graph is shown below. 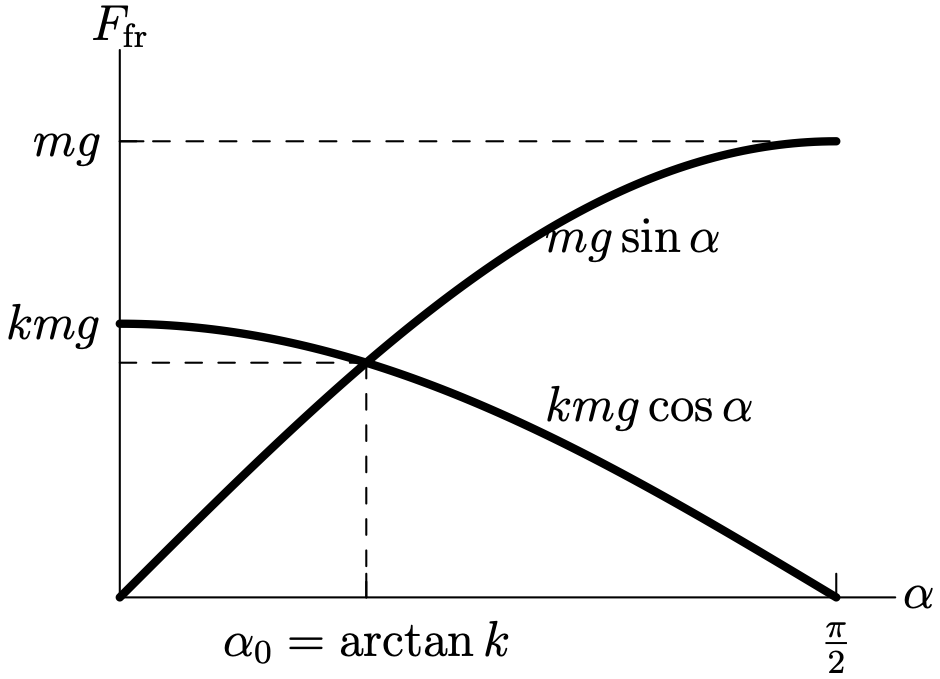
Hint
The motion of a body located on an inclined plane becomes possible if $mg \sin \alpha \ge kmg \cos \alpha$, i.e., at an angle $\alpha \ge \alpha_0 = \arctan k$. If $\alpha < \alpha_0$, the body is at rest and the friction force is equal to $mg \sin \alpha$ (see problem 23). If $\alpha \ge \alpha_0$, then $F_{\text{fr}} = F_{\text{fr.max}} = kmg \cos \alpha$.
26. Estimate the friction coefficient $k$ of sand on sand if the angle of a sandpile is $\alpha$.
Answer
$k = \tan \alpha$.
27. A cord is thrown over a light, frictionless pulley. At one end of the cord, a mass $m_1$ is attached. On the other end, a ring of mass $m_2$ can slide along the cord (see figure).
- With what acceleration $a$ does the ring move if the mass $m_1$ is stationary? What is the friction force $F_{\text{fr}}$ between the ring and the cord?
- The ring slides down with a constant acceleration $a_2$ relative to the cord. Find the acceleration $a_1$ of the mass $m_1$, and the friction force $F_{\text{fr}}$ between the ring and the cord. The mass of the cord can be neglected; assume the mass $m_1$ is descending.
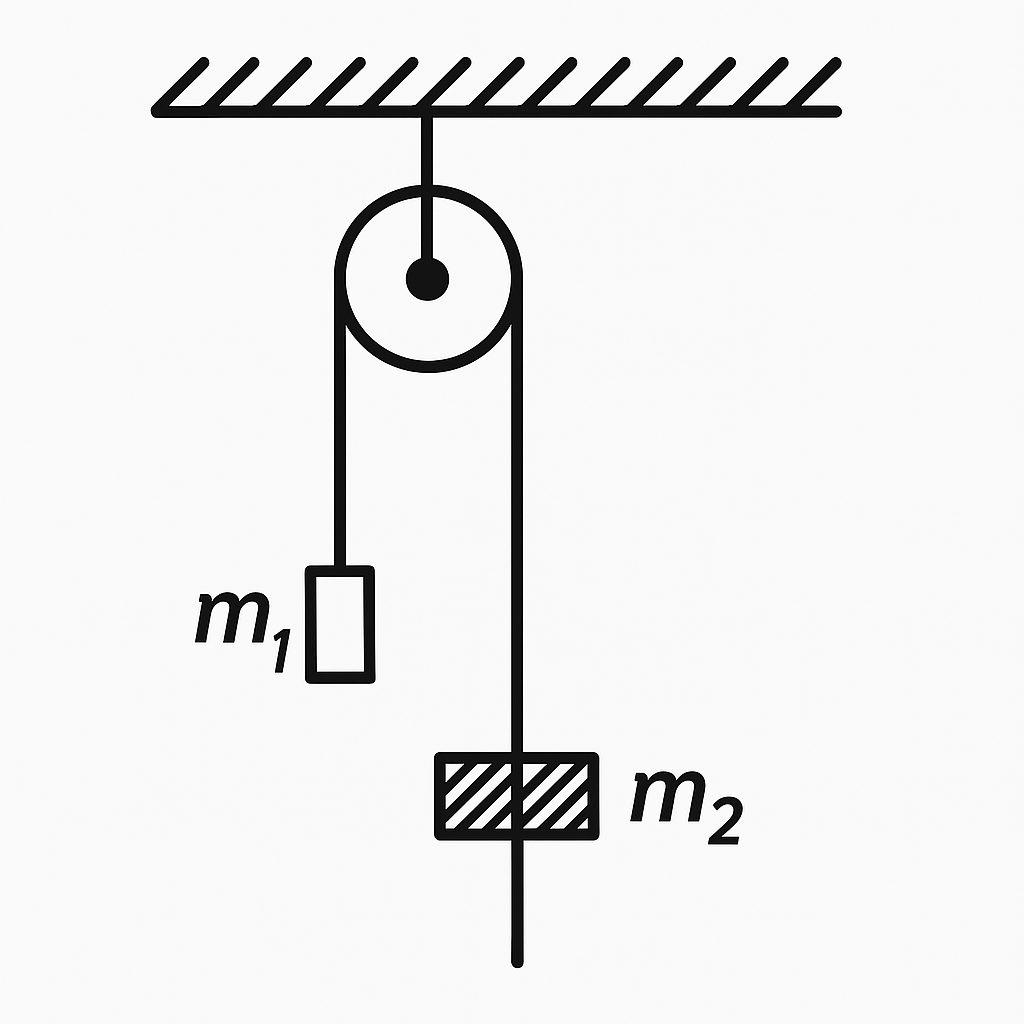
Answer
1. $a = (1 - m_1/m_2)g$; $F_{\text{fr}} = m_1 g$.
- $a_1 = \dfrac{m_1 g - m_2(g-a_2)}{m_1+m_2}$; $F_{\text{fr}} = \dfrac{m_1 m_2 (2g - a_2)}{m_1+m_2}$.
Hint
1. Since weight $m_2$ is stationary, the tension of the string, and consequently, the friction force of the ring on the string are equal to $m_2 g$. [Note: Error in original text, should be $m_1 g$ based on context].
- The friction force is equal to the tension force of the string, and the acceleration of the ring relative to the block is $a_2 - a_1$. The equations of motion for the weights are expressed as follows: $m_1 a_1 = m_1 g - F_{\text{fr}};$ $m_2(a_2 - a_1) = m_2 g - F_{\text{fr}}.$
28. A body of mass $M$ moves with acceleration $a$ on a horizontal plane under force $F$ at angle $\alpha$. Find $F$ if the friction coefficient is $k$.
Answer
$F = \dfrac{M(kg+a)}{\cos \alpha + k \sin \alpha}$.
Hint
The normal pressure force is $Mg - F \sin \alpha$ (see figure, a) or $Mg + F \sin \alpha$ (see figure, b) depending on the direction of action of force $\vec{F}$. 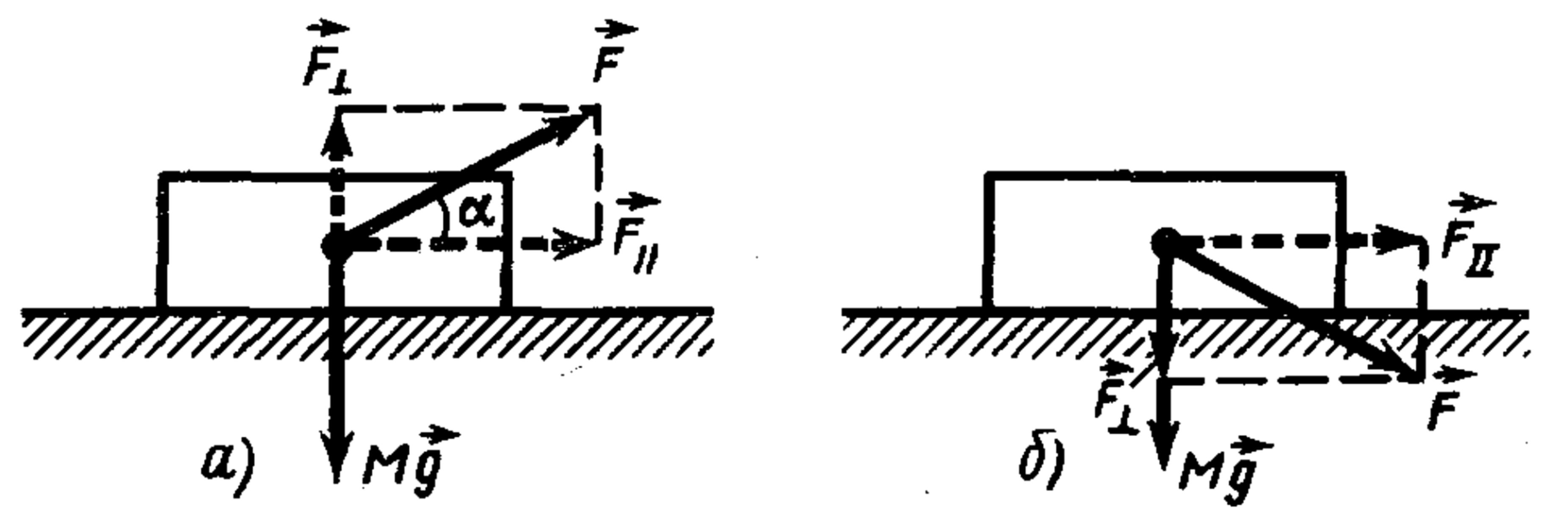
29. Board $A$ moves on a table under tension from a cord attached to board $B$ hanging over a pulley.
- Find the tension $T$ if $m_A = 200, \text{g}$, $m_B = 300, \text{g}$, and $k = 0.25$. Neglect pulley mass.
- How does the answer change if the boards are swapped? 3. Find the force $F$ on the pulley's axle in both cases.
Answer
1. $T = g \frac{m_1 m_2 (1+k)}{m_1+m_2} = 1.47$ H. 2. Does not change. 3. $F = 2.08$ H.
30. Two masses $m_1$ and $m_2$ (see figure) are in an elevator ascending at $a$. Find the cord tension $T$ if $m_1