1. A thread with a weight suspended from it is deflected by an angle $\alpha$ and released. At what angle $\beta$ will the thread with the weight deflect if, during its motion, it is stopped by a pin placed vertically at the midpoint of the thread's length?
Answer
$\beta = \arccos(2 \cos \alpha - 1)$.
2. 1. A body is thrown vertically upward with a velocity $v_0 = 16 \, \text{m/s}$. At what height $h$ will the kinetic energy of the body equal its potential energy?
- With what initial velocity must a ball be thrown from a height $h$ so that it bounces to a height $2h$? Assume the collision is elastic and air resistance is negligible.
Answer
1. $h = v_0^2 / (4g) \approx 6.5$ m.
- $v_0 = \sqrt{2gh}$.
3. A stone is thrown horizontally from a tower of height $H = 25 \, \text{m}$ with a velocity $v_0 = 15 \, \text{m/s}$. Find the kinetic and potential energies of the stone one second after the motion begins. The mass of the stone is $m = 0.2 \, \text{kg}$. Neglect air resistance.
Answer
$T = 32.2$ J; $\Pi = 39.4$ J.
Hint
The initial values of kinetic and potential energy are respectively: $T = mv_0^2/2$,\qquad \Pi = mgH.$ The change in potential energy $\Delta \Pi = mg\Delta h$, where $\Delta h = gt^2/2$ (taking $t=1$ s) is the change in the body's height over 1 s. The kinetic energy of the body increases by this same amount.
4. Determine the kinetic energy of a body with a mass of 1 kg, thrown horizontally with a velocity of $20 \, \text{m/s}$, at the end of the fourth second of its motion. Assume $g = 10 \, \text{m/s}^2$.
Answer
$T = 1000$ J.
Solution
At the end of the fourth second, the velocity of the body, thrown horizontally with speed $v_0$ from some height, will be composed of the horizontal velocity $v_0$ and the vertical velocity $v_y = gt$. The velocity of the body $\vec{v}$ is found using the parallelogram rule (see fgigure). Hence, the kinetic energy of the body at the end of the fourth second is $ T = \dfrac{mv^2}{2} = \dfrac{m}{2} [v_0^2 + (gt)^2]. $ (see figure) 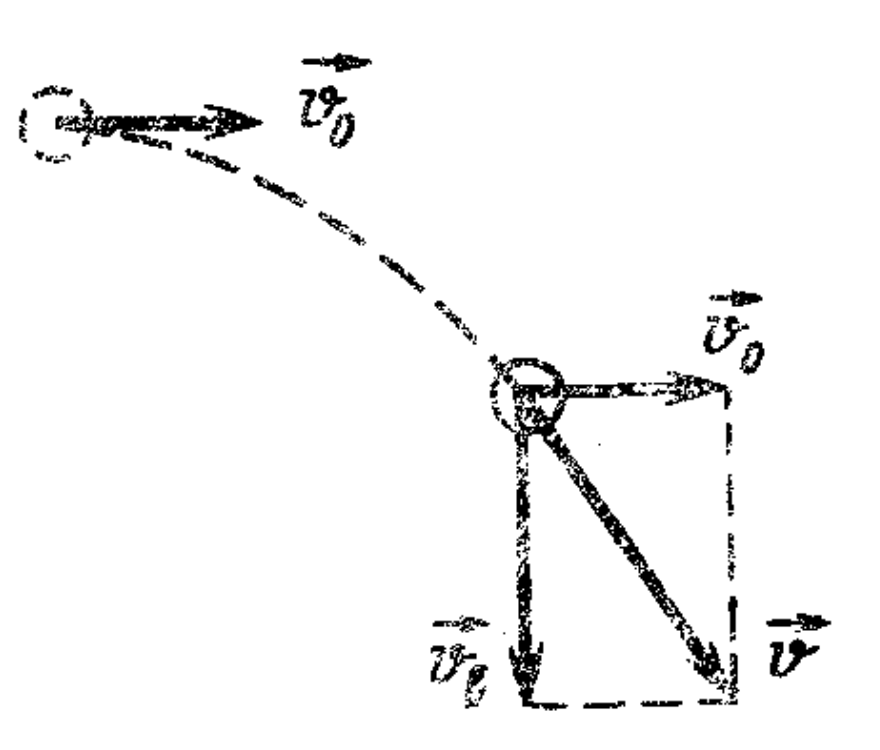
5. A flexible uniform rope of length $L$ lies on a smooth horizontal table. One end of the rope is at the edge of the table. At some moment, a slight push sets the rope in motion, causing it to slide off the table continuously. How do the acceleration and velocity of the rope depend on the length $x$ of the hanging part? What will be the velocity of the rope when it completely slides off the table?
Answer
$a = xg/L$; $v = x\sqrt{g/L}$; $v_{final} = \sqrt{gL}$.
Solution
The entire rope is accelerated by the force of gravity acting on the hanging part $F_g = mxg/L$, where $m$ is the mass of the rope. According to Newton's second law, $mxg/L = ma$. Hence $a = xg/L$. The speed of the rope can be found from the law of conservation of energy. If a part of the rope of length $x$ slides off the table, its center of mass descends by $h = x/2$, therefore $mgx^2/(2L) = mv^2/2$. Hence $v = x\sqrt{g/L}$ and $v_{final} = \sqrt{gL}$.
6. A rope of length $L$ is thrown over a peg. Initially, the ends of the rope are at the same level. After a slight push, the rope starts moving. Determine the velocity $v$ of the rope when it slides off the peg. Neglect friction.
Answer
$v = \sqrt{gL/2}$.
Hint
See the solution to problem 5. Initially, the center of mass of the rope was at a distance $L/4$ from the peg, and at the moment the rope leaves the peg, its center of mass will be at a distance $L/2$ from the peg.
7. A skater, having accelerated to a velocity $v = 27 \, \text{km/h}$, enters an icy hill. To what height $H$ from the initial level will the skater ascend if the hill rises $h = 0.5 \, \text{m}$ for every $s = 10 \, \text{m}$ horizontally? The coefficient of friction between the skates and the ice is $k = 0.02$.
Answer
$H \approx 2$ m.
Solution
The decrease in the mechanical energy of the skater is equal to the work done against friction: $ \dfrac{mv^2}{2} - mgH = A_{fr} \tag{1} $ Here $H$ is the height to which the skater ascends; on the other hand, $ \begin{aligned} A_{fr} &= kmgl \cos \alpha \\ &= k \dfrac{H}{\sin \alpha} mg \cos \alpha \\ &= k \dfrac{mgH}{s} \end{aligned}\tag{2} $ where $l$ is the path traveled by the skater along the inclined plane. Substituting expression (2) into equation (1), we find that $ H = \dfrac{v^2}{2g(1 + k/s)} $.
8. A body of mass $m = 1.5 \, \text{kg}$ is thrown vertically upward from a height $h = 4.9 \, \text{m}$ with a velocity $v_0 = 6 \, \text{m/s}$ and falls to the ground with a velocity $v = 5 \, \text{m/s}$. Determine the work done by air resistance forces.
Answer
$A \approx -80.2$ J.
Hint
The work done by resistance forces is equal to the change in the mechanical energy of the body: $ A = E_2 - E_1 = \dfrac{mv_2^2}{2} - \left( mgh + \dfrac{mv_1^2}{2} \right). $
9. A stone with a mass of 50 g is thrown at an angle to the horizontal from a height of 20 m above the ground with a velocity of 18 m/s and lands with a velocity of 24 m/s. Find the work done to overcome air resistance.
Answer
$A \approx 3.5$ J.
Hint
See problem 8. The work done against resistance forces is positive.
10. An airplane with a mass $m = 10^3 \, \text{kg}$ flies horizontally at an altitude $H = 1200 \, \text{m}$ with a velocity $v_1 = 50 \, \text{m/s}$. The engine is then turned off, and the plane transitions to a gliding flight, reaching the ground with a velocity $v_2 = 25 \, \text{m/s}$. Determine the average air resistance force during the descent, assuming the descent path is 8 km long.
Answer
$F_{res} \approx 1570$ N.
Hint
The work done by resistance forces $A = \dfrac{mv_2^2}{2} - \left( \dfrac{mv_1^2}{2} + mgH \right)$. On the other hand, $A = -F_{res}l$ ($F_{res}$ is the average resistance force, which is directed opposite to the displacement, $l$ is the length of the slope).
11. A body of mass $m = 1 \, \text{kg}$ moves across a table with an initial velocity $v_0 = 2 \, \text{m/s}$. Upon reaching the edge of the table, which is $h = 1 \, \text{m}$ high, the body falls. The coefficient of friction between the body and the table is $k = 0.1$. Determine the amount of heat released during the inelastic collision with the ground. The path traveled by the body on the table is $s = 2 \, \text{m}$.
Answer
$Q \approx 9.8$ J.
Hint
From the law of conservation of energy, it follows that $ mgh + \dfrac{mv_0^2}{2} = kmgs + Q, $ where $Q$ is the amount of heat released during the impact.
12. A weight attached to a vertical spring is slowly lowered to its equilibrium position, stretching the spring by a length $x_0$. How much will the spring stretch if the same weight is allowed to fall freely from a position where the spring is unstretched? What maximum velocity $v_{\text{max}}$ will the weight attain? Describe the nature of the weight's motion. The mass of the weight is $m$. Neglect the mass of the spring.
Answer
$x_{\text{max}} = 2x_0$; $v_{\text{max}} = \sqrt{gx_0}$; oscillatory.
Solution
From the equilibrium condition of the load $mg = kx_0$, we find the spring stiffness $k = mg/x_0$. Now writing the law of conservation of energy $kx^2/2 = mgx$ and substituting the expression for $k$ into the equation, we find $x = 2x_0.$ The speed of the load is maximum when the acceleration is zero and $mg = kx$. Since $mg = kx_0$, this occurs at $x=x_0$. The energy conservation at this point is $\dfrac{mv_{\text{max}}^2}{2} + \dfrac{kx_0^2}{2} = mgx_0.$ Substituting $k=mg/x_0$, we get $\dfrac{mv_{\text{max}}^2}{2} + \dfrac{mgx_0}{2} = mgx_0,$ so $v_{\text{max}} = \sqrt{gx_0}$. The load will oscillate around the equilibrium position $x_0$ with amplitude $x_0$ (from $x=0$ to $x=2x_0$).
13. A falling weight of mass $M = 5 \cdot 10^2 \, \text{kg}$ drives a pile into the ground from a height $h = 1.2 \, \text{m}$. The pile sinks $s = 2 \, \text{cm}$ into the ground upon impact. Determine the average force of impact $F_{cp}$ and its duration $\tau$, assuming the mass of the pile is much smaller than the mass of the weight.
Answer
$F_{res} = Mg(1 + h/s) \approx 3 \times 10^5$ N; $\tau = 2s/\sqrt{2gh} \approx 8 \times 10^{-3}$ s.
Solution
The work done against the resistance force of the soil is equal to the change in potential energy of the pile: $F_{res}s = Mg(h + s)$. Hence $F_{res} = Mg(1 + h/s) = Mg \dfrac{h+s}{s} \approx 3 \times 10^5$ N. The impact time is determined from the relation $\tau = s/v_{avg} = 2s/v_0$, where $v_0$ is the speed of the pile at the beginning of the impact (we assume the motion of the pile is uniformly decelerated, so $v_{avg} = v_0/2$). In accordance with the law of conservation of energy $v_0 = \sqrt{2gh}$. Therefore $\tau = 2s/\sqrt{2gh} \approx 8 \times 10^{-3}$ s.
14. A sled slides down a hill of height $h = 2 \, \text{m}$ and base $b = 5 \, \text{m}$, then stops after traveling a horizontal distance $l = 35 \, \text{m}$ from the base of the hill. Find the coefficient of friction.
Answer
$k = 0.05$.
Solution
At the end of the path, the sled stops, and, consequently, all the initial potential energy is spent on work against friction forces on the inclined and horizontal sections of the path: $ mgh = kmgs \cos \alpha + kmgl, \tag{1} $ where $s$ is the length of the slope; $\alpha$ is the angle of inclination of the hill. In this case $s \cos \alpha = b$. Therefore, from equation (1) we get $h = k(b + l)$, whence $k = h/(b + l)$.
15. A steel ball of mass $m = 20 \, \text{g}$ falls from a height $h_1 = 1 \, \text{m}$ onto a steel plate and rebounds to a height $h_2 = 81 \, \text{cm}$. Find: a) the impulse of the force acting on the plate during the collision; b) the amount of heat released during the collision.
Answer
a) $p = 0.17$ N·s;
b) $Q = 3.7 \times 10^{-2}$ J.
Solution
The impulse of the force acting on the ball during the impact with the plate, in accordance with Newton's second law, is equal to: $ p = |\Delta (m\vec{v})| = m(v_1 + v_2), $ where $v_1$ and $v_2$ are the speeds of the ball respectively before and after the impact. From the law of conservation of energy, we find: $v_1 = \sqrt{2gh_1}$ and $v_2 = \sqrt{2gh_2}$, therefore $p = m\sqrt{2g}(\sqrt{h_1} + \sqrt{h_2})$. According to Newton's third law, the impulse of the force that acted on the plate during the impact is numerically equal to $p$. The amount of heat released during the impact of the ball on the plate is equal to the difference in the ball's energies before and after the impact: $ Q = \dfrac{mv_1^2}{2} - \dfrac{mv_2^2}{2} = mg(h_1 - h_2). $
16. A light ball begins to fall freely and, after traveling a distance $l$, collides elastically with a heavy plate moving upward with a velocity $u$. To what height $h$ will the ball rebound after the collision?
Answer
$h = (\sqrt{2gl} + 2u)^2 / (2g)$.
Solution
It is more convenient to solve the problem by considering the collision in a coordinate system associated with the moving plate. Since the speed of the plate changes negligibly due to the impact, this coordinate system can be considered inertial. In it, the ball before the impact with the plate has speed $v' = v + u$, where $v = \sqrt{2gl}$ is the speed of the ball in the stationary coordinate system associated with the Earth. The impact of the ball on the plate is perfectly elastic, therefore, after the impact, the ball in the moving system will have speed $v_1' = -v' = -(v + u)$. In the coordinate system associated with the Earth, the speed of the ball will be $v_1 = -(v + u) - u = -(v + 2u)$ (the minus sign means that the ball will have a velocity directed upwards). Therefore, after the impact, the ball will bounce to a height $h = \frac{v_1^2}{2g} = \frac{(v + 2u)^2}{2g} = \frac{(\sqrt{2gl} + 2u)^2}{2g}.$
17. A balloon held by a rope rises to a certain height. How does the potential energy of the balloon-air-Earth system change?
Answer
The potential energy of the ball-air-Earth system decreased, because as the ball rises, the volume occupied by the ball is replaced by air, which has a greater mass than the ball.
18. A hockey puck with an initial velocity $v_0 = 5 \, \text{m/s}$ slides a distance $s = 10 \, \text{m}$ before hitting the boards. The collision is perfectly elastic, the coefficient of friction between the puck and the ice is $k = 0.1$, and air resistance is negligible. Determine the distance $l$ the puck will travel after the collision.
Answer
$l \approx 2.7$ m.
Hint
During the motion of the puck, its kinetic energy is spent on doing work against friction: $mv_0^2/2 = kmg(s + l).$
19. A body slides without friction off a wedge lying on a horizontal plane twice: first, the wedge is fixed; second, the wedge can slide without friction. Will the speed of the body at the end of the slide be the same in both cases if the body starts from the same height each time?
Answer
In the first case, the speed of the body is greater than in the second.
20. Why is it difficult to jump to shore from a light boat near the shore, but easy to do so from a steamship at the same distance?
Solution
Let $v$ denote the minimum speed with which the person must jump to reach the shore. During the jump, the person imparts a velocity $u$ to the boat (or steamship), equal, based on the law of conservation of momentum, to $u = mv/M$ where $m$ is the mass of the person and $M$ is the mass of the boat or steamship.
By jumping, the person performs work $A$, equal to the kinetic energy acquired by the person and the boat (or steamship):
$A = \dfrac{mv^2}{2} + \dfrac{Mu^2}{2} = \dfrac{mv^2}{2} \left( 1 + \dfrac{m}{M} \right). $
This work is smaller, the smaller the ratio of the masses of the person and the boat (steamship). The mass of the steamship is many times greater than the mass of the person ($m/M \ll 1$), therefore, jumping from it, the person performs less work than in the case when they jump from the boat ($m/M \approx 1$).
21. A skater of mass $M = 70 \, \text{kg}$, standing on ice skates on ice, throws a stone of mass $m = 3 \, \text{kg}$ horizontally with a velocity $v = 8 \, \text{m/s}$ relative to the Earth. Find the distance $s$ the skater will recoil if the coefficient of friction between the skates and the ice is $k = 0.02$.
Answer
$s = \left( \dfrac{m}{M} \right)^2 \dfrac{v^2}{2kg} \approx 0.29$ m.
Solution
Based on the laws of conservation of momentum and energy, we can write the equations: $Mv' = mv\quad\text{ and }\quad M\frac{(v')^2}{2} = kMgs$. Excluding $v'$ from these equations, we find $s = \left( \dfrac{m}{M} \right)^2 \dfrac{v^2}{2kg}.$
22. A person stands on a stationary cart and throws a stone of mass $m = 8 \, \text{kg}$ horizontally with a velocity $v_1 = 5 \, \text{m/s}$ relative to the Earth. Determine the work done by the person if the mass of the cart with the person is $M = 160 \, \text{kg}$. Analyze the dependence of the work on the mass $M$. Neglect friction.
Answer
$A \approx 105$ J.
Solution
The work that the person performs by throwing a stone from the cart is spent on imparting kinetic energy to the stone and the cart with the person: $A = \dfrac{mv_1^2}{2} + \dfrac{Mv_2^2}{2}, $ where $v_2$ is the speed of the cart. By the law of conservation of momentum, $mv_1 = Mv_2$, whence $v_2 = mv_1/M$; substituting $v_2$ into the expression for work, we get $ A = \dfrac{mv_1^2}{2} + \dfrac{m^2v_1^2}{2M} = \dfrac{mv_1^2}{2} \left( 1 + \dfrac{m}{M} \right). $ If $M \gg m$, then $A \approx mv_1^2/2$, i.e., all the work done by the person goes into imparting kinetic energy to the stone. In the general case, the kinetic energies acquired by the interacting bodies are inversely proportional to their masses.
23. A rifle of mass $M = 3 \, \text{kg}$ is suspended horizontally by two parallel threads. When fired, it recoils and deflects upward by $h = 19.6 \, \text{cm}$. The mass of the bullet is $m = 10 \, \text{g}$. Determine the velocity $v_1$ of the bullet as it exits the barrel. 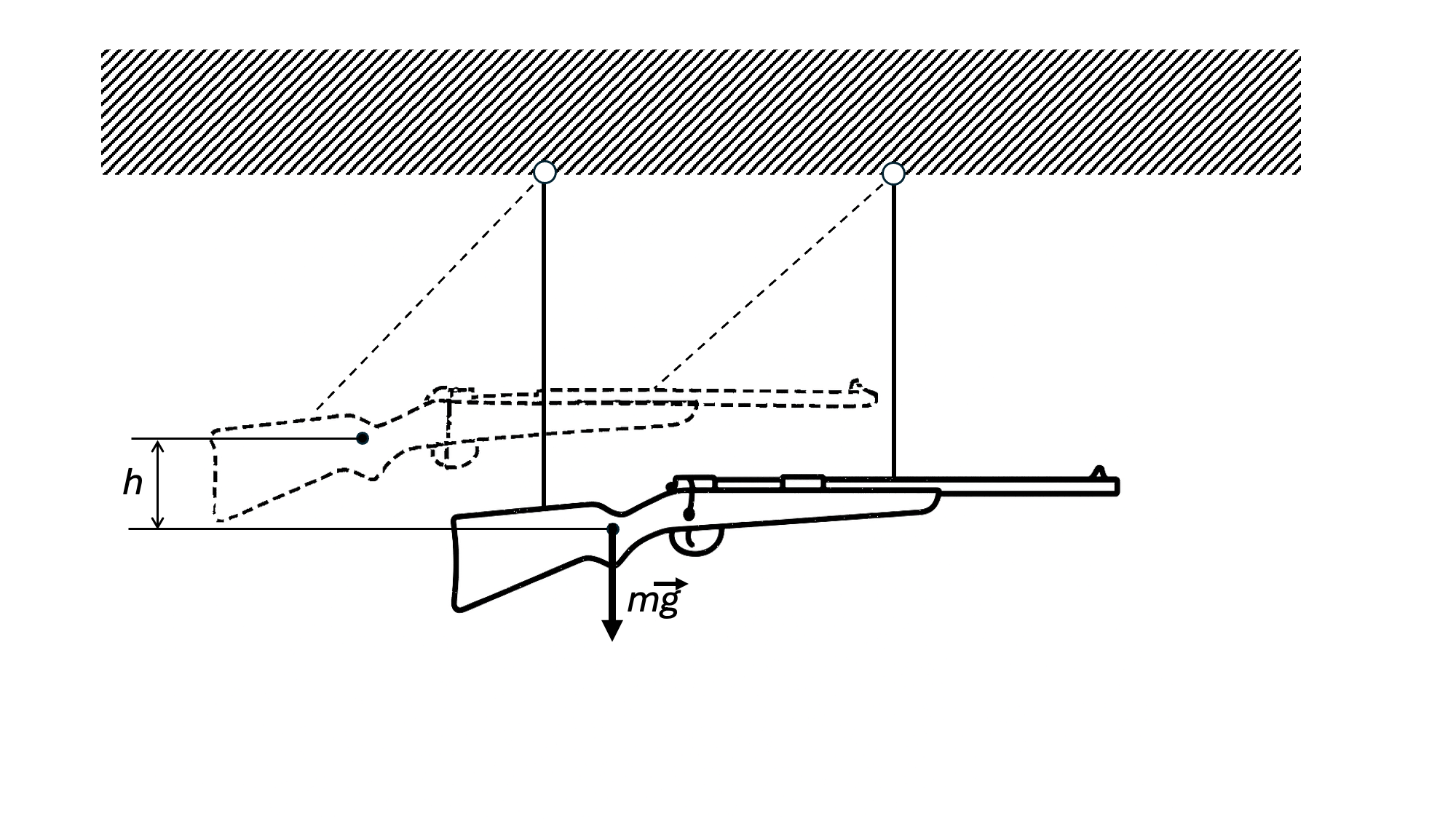
Answer
$v_1 \approx 590$ m/s.
Solution
Based on the law of conservation of energy, we determine the recoil speed of the rifle after the shot $v$ (figure above): $Mgh = Mv^2/2$,\qquad v^2 = 2gh.$ At the moment of firing, only the pressure forces of the powder gases act on the rifle and the bullet. These are internal forces. Therefore, the rifle-bullet system can be considered closed and the law of conservation of momentum can be applied to it. Before the shot, the momentum of the system was zero, therefore, after the shot, the total momentum of the system must also be zero: $M\vec{v} + m\vec{v}_1 = 0.$ Hence $v_1 = -\dfrac{Mv}{m} = -\dfrac{M}{m} \sqrt{2gh}.$ The '$-