1. From points $A$ and $B$, separated by a distance $l$, two bodies start moving simultaneously towards each other: the first with velocity $v_1$, the second with $v_2$. Determine the time until they meet and the distance from point $A$ to the meeting point. Solve the problem graphically as well.
Answer
$t_c =\dfrac{l}{v_1 + v_2}$; $x_c = \dfrac{lv_1}{v_1 + v_2}$.
Solution
The dependence of the coordinates of the bodies on time is given by the formulas: $x_1 = v_1 t; \quad x_2 = l - v_2 t.$ The meeting ($x_1 = x_2$) will occur after time $t = l/(v_1 + v_2)$ from the start of motion at a point located at a distance $lv_1/(v_1 + v_2)$ from point A. The graphs of the dependence of the coordinates of the bodies on time are shown below ($\tan \alpha = v_1$; $\tan \beta = -v_2 < 0$, since $v_2$ is directed in the opposite direction to the one taken as positive). The moment of meeting corresponds to point C of intersection of the graphs.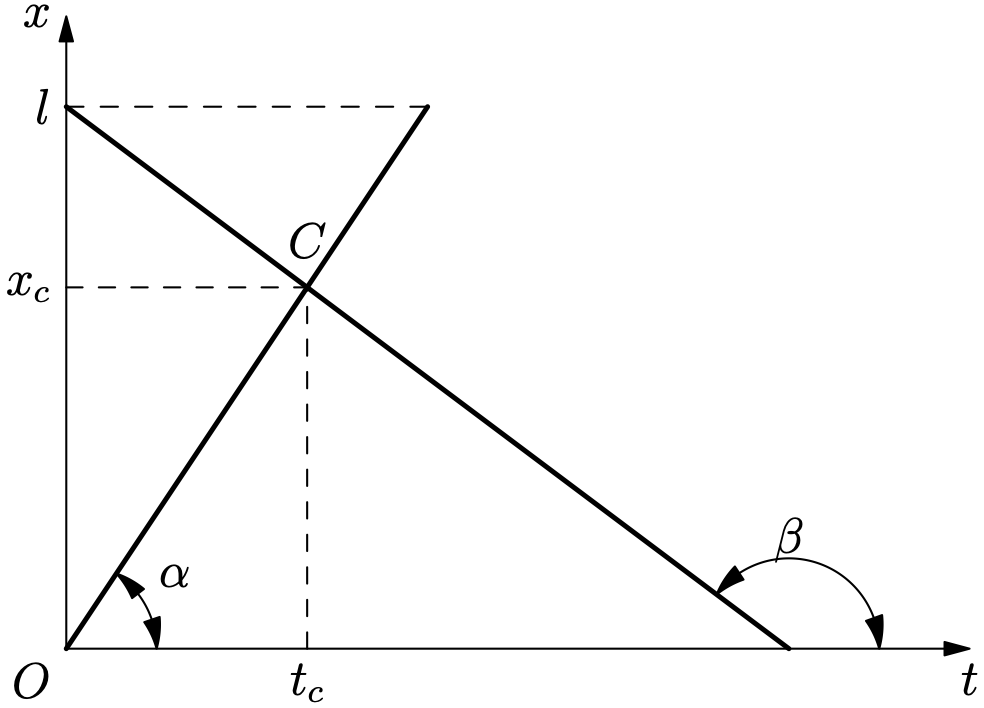
2. After how much time and where would the bodies (see See Problem 1) meet if they moved in the same direction $A \rightarrow B$, with the body from point $B$ starting to move $t_0$ seconds after the body from point $A$?
Answer
$t_c = \dfrac{l - v_2 t_0}{v_1 - v_2}$; $x_c = \dfrac{(l - v_2 t_0) v_1}{v_1 - v_2}$.
Hint
Use the graphs of the dependence of the coordinates of the bodies on time (the following figure). 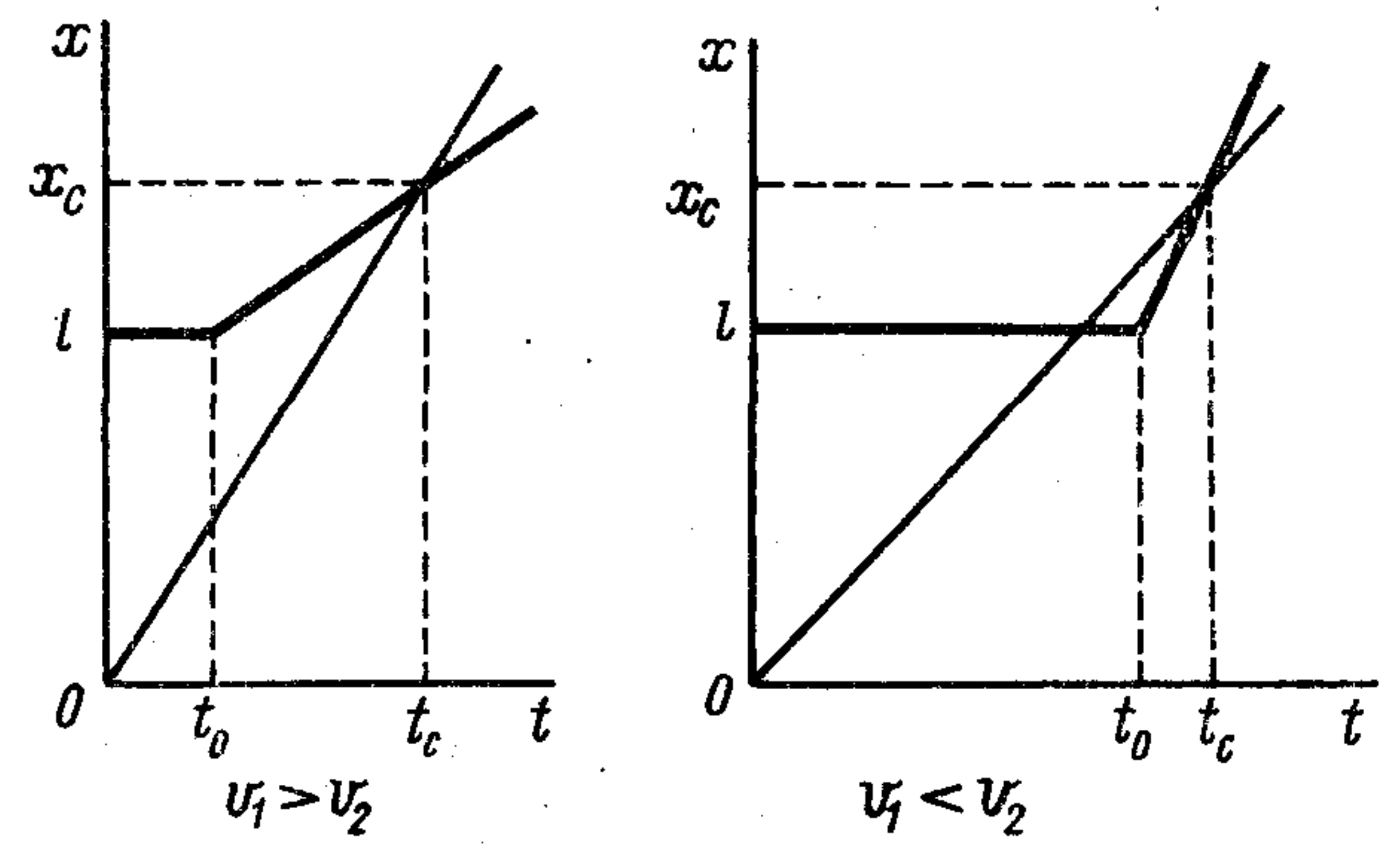
3. A motorboat covers the distance between two points $A$ and $B$ downstream in time $t_1 = 3\, \text{h}$, while a raft takes $t = 12\, \text{h}$. How much time $t_2$ will the motorboat take for the return journey?
Answer
$t_2 = 6$ h.
Solution
Let $u$ be the speed of the current, and $v$ be the speed of the boat relative to the water, we can write: $t_1 = \dfrac{s}{v+u}; \tag{1}$ $t = \dfrac{s}{u}. \tag{2}$ To determine the time $t_2 = s/(v-u)$ taken by the boat for the return trip, it is convenient to rewrite equations (1) and (2) as follows: $\dfrac{1}{t_1} = \dfrac{v}{s} + \dfrac{u}{s}; \tag{3}$ $\dfrac{1}{t} = \dfrac{u}{s}. \tag{4}$ Subtracting twice equation (4) from equation (3), we get $\dfrac{1}{t_1} - \dfrac{2}{t} = \dfrac{v}{s} - \dfrac{u}{s} = \dfrac{1}{t_2},$ whence $t_2 = \dfrac{t t_1}{t - 2t_1}.$
4. An escalator in the metro descends a person walking down it in 1 minute. If the person walks twice as fast, they descend in 45 seconds. How much time does it take for a person standing still on the escalator to descend?
Answer
1.5 min.
5. A person runs on an escalator. The first time, they count $n_1 = 50$ steps; the second time, moving in the same direction at three times the speed, they count $n_2 = 75$ steps. How many steps would they count on a stationary escalator?
Answer
$n = 100$.
Solution
If the person’s velocity were directed opposite to the motion of the escalator, then the faster he walked, the fewer steps he would count (but no fewer than $ n$. In our case, the directions of the person’s and the escalator’s motion coincide.
Let $v$ be the speed of the escalator; $l$ its length, and $n$ the number of steps on a stationary escalator. The number of steps per unit length of the escalator is $n / l$.
Therefore, if the person walks with speed $u$ relative to the escalator, the time spent on the escalator is $l / (v + u)$, and the distance he travels (relative to the escalator) is $ul / (v + u)$.
Thus, the number of steps the person counts is:
$n_1 = \dfrac{ul}{v + u} \cdot \dfrac{n}{l} = \dfrac{u}{v + u} n.$
Similarly, in the second case (if the walking speed is tripled), he counts:
$n_2 = \dfrac{3ul}{v + 3u} \cdot \dfrac{n}{l} = \dfrac{3u}{v + 3u} n.$
Hence, we obtain the following system of equations:
From this, by eliminating the ratio $v/u$, we find:
$n = \dfrac{2n_1 n_2}{3n_1 - n_2} = 100.$
6. Between two points on a river, located $s = 100\, \text{km}$ apart, a boat shuttles. Going downstream, it covers this distance in $t_1 = 4\, \text{h}$, and upstream in $t_2 = 10\, \text{h}$. Determine the river's current speed and the boat's speed $v$ relative to the water.
Answer
$u = 7.5$ km/h; $v = 17.5$ km/h.
7. A raft passes by a dock. At that moment, a motorboat departs downstream to a village located $s_1 = 15\, \text{km}$ from the dock. The boat reaches the village in $t = 3/4\, \text{h}$ and, turning back, meets the raft at a distance $s_2 = 9\, \text{km}$ from the village. What are the river's current speed and the boat's speed relative to the water?
Answer
$u = 4$ km/h; $v = 16$ km/h.
Solution
Let's choose the raft (water) as the reference frame. In this reference frame, the boat moves down and up the river with the same speed. This means that the time for the boat to move away from the raft is equal to the time to approach it; thus, the boat also returned in 3/4 h. During the elapsed 1.5 h, the raft traveled a distance $s_1-s_2 = 6 \text{ km}.$ Consequently, the speed of the current (speed of the raft relative to the bank) is $u = 6 / 1.5 = 4~ \text{km/h}.$ The speed of the boat relative to the water $v = \dfrac{s_1}{t} - u = 16~\text{km/h}.$
This solution illustrates how important a successful choice of reference frame is in kinematics.
8. A column of troops marches at a speed of $v_1 = 5\, \text{km/h}$, stretched along a road for a distance $l = 400\, \text{m}$. A commander at the rear sends a cyclist with a message to the lead detachment. The cyclist rides at $v_2 = 25\, \text{km/h}$, delivers the message, and immediately returns at the same speed. How much time $t$ after receiving the message does the cyclist return?
Answer
$t = 2$ min.
Hint
The speed of the cyclist in the reference frame associated with the column is $v_2 - v_1$ when moving towards the head of the column, and $v_2 + v_1$ when returning. Therefore $t = \dfrac{l}{v_2 - v_1} + \dfrac{l}{v_2 + v_1} = \dfrac{2lv_2}{v_2^2 - v_1^2}.$
9. A train car of width $d = 2.4\, \text{m}$, moving at $v = 15\, \text{m/s}$, is pierced by a bullet flying perpendicular to the car's motion. The displacement of the holes in the car's walls relative to each other is $l = 6\, \text{cm}$. What is the bullet's speed?
Answer
600 m/s.
10. What is the speed $v_2$ of vertically falling raindrops if a car driver notices that the drops leave no trace on the rear window, tilted forward at an angle $\alpha = 60^\circ$ to the horizon, when the car's speed $v_1$ exceeds 30 km/h?
Answer
$v_2 = v_1 \tan \alpha \approx 14.4$ m/s.
Solution
For the raindrops not to leave a trace on the rear window, the direction of the raindrop velocity vector relative to the car must make an angle with the horizon no greater than $60^\circ$. The relative velocity is composed of the vertical component, equal to the falling speed of the drop $v_2$, and the horizontal component, equal to the speed of the car $-v_1$ and directed in the opposite direction (following figure). From the velocity triangle, it is clear that $v_2 = v_1 \tan \alpha$.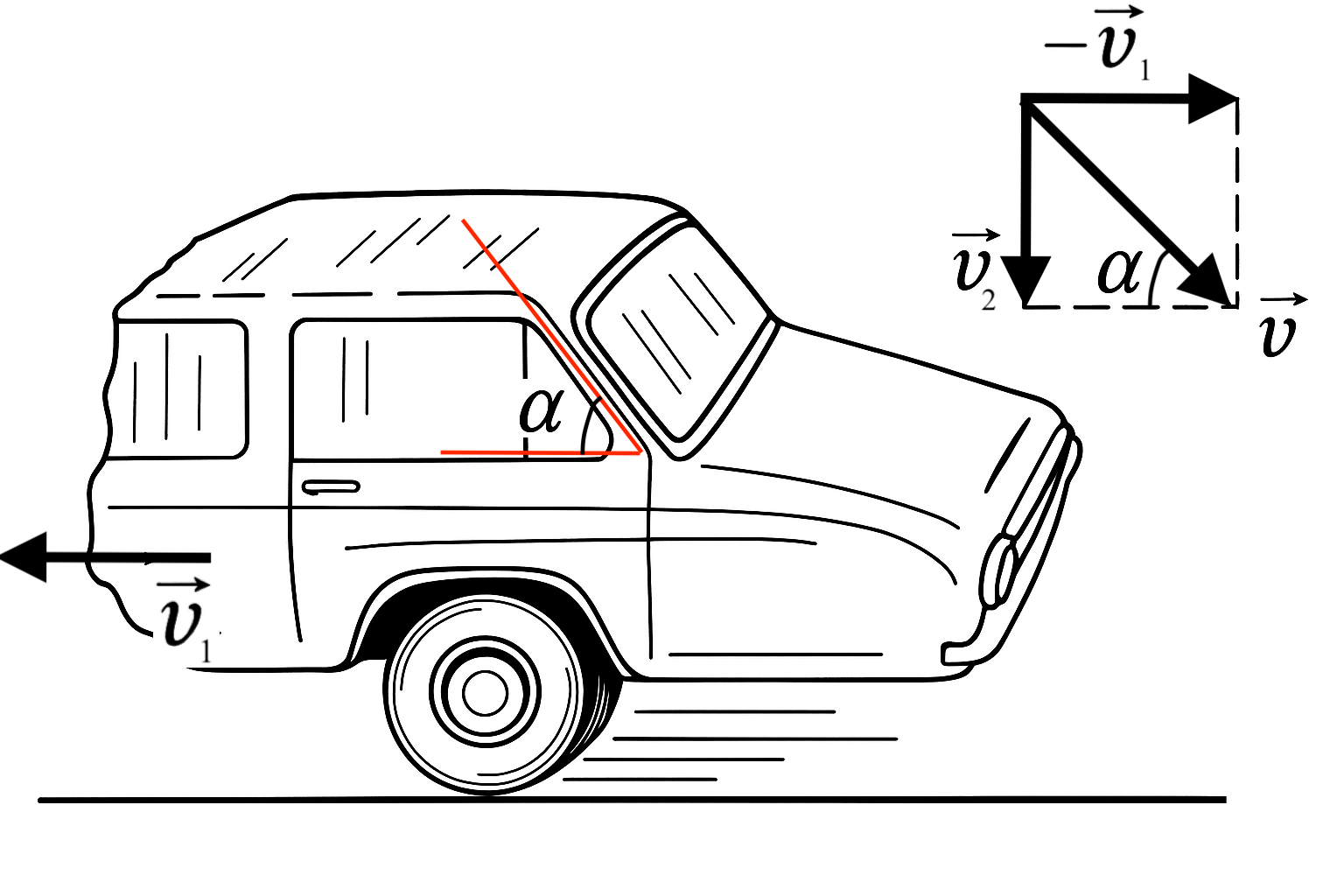
11. It is raining outside. In which case will a bucket standing in the back of a truck fill faster with water: when the truck is moving or when it is stationary?
Answer
Identical.
12. At what speed $v$ and course must an airplane fly to cover a path of $s = 300\, \text{km}$ due North in time $t = 2\, \text{h}$, if a northwest wind blows at an angle $\alpha = 30^\circ$ to the meridian with speed $u = 27\, \text{km/h}$ during the flight?
Answer
$v = 174$ km/h; northwest at an angle $4^\circ 27'$ to the meridian.
Hint
Let $v_0 = s/t$ be the speed of the aircraft relative to the Earth. It is directed, according to the condition, along the meridian; then $\vec{v}_0 = \vec{v} + \vec{u}$. By the cosine theorem $v^2 = u^2 + v_0^2 - 2uv_0 \cos 150^\circ.$ The angle $\beta$ between $\vec{u}$ and $\vec{v}_0$ is found from the sine theorem: $\sin \beta / u = \sin 150^\circ / v.$
13. A blackboard moves on a smooth horizontal table at speed $v$. What shape will chalk leave as a trace on the board if it is thrown horizontally at speed $u$ perpendicular to the board's motion, assuming: a) negligible friction between the chalk and the board; b) significant friction?
Answer
a) and b) - a straight line forming an angle $\alpha = \arctan(u/v)$ with the direction of motion of the board. In case b), the trace may not reach the edge of the board.
Hint
Consider the motion of the chalk in the coordinate system associated with the board. Since the friction force is directed along the velocity vector of the chalk relative to the board, it cannot change the direction of the chalk's motion and only reduces its speed.
14. A ship departs from point $A$ at speed $v$, making an angle $\alpha$ with the line $AB$ (following figure). At what angle $\beta$ to the line $AB$ should a torpedo be launched from point $B$ to hit the ship? The torpedo must be launched when the ship is at point $A$. The torpedo's speed is $u$. 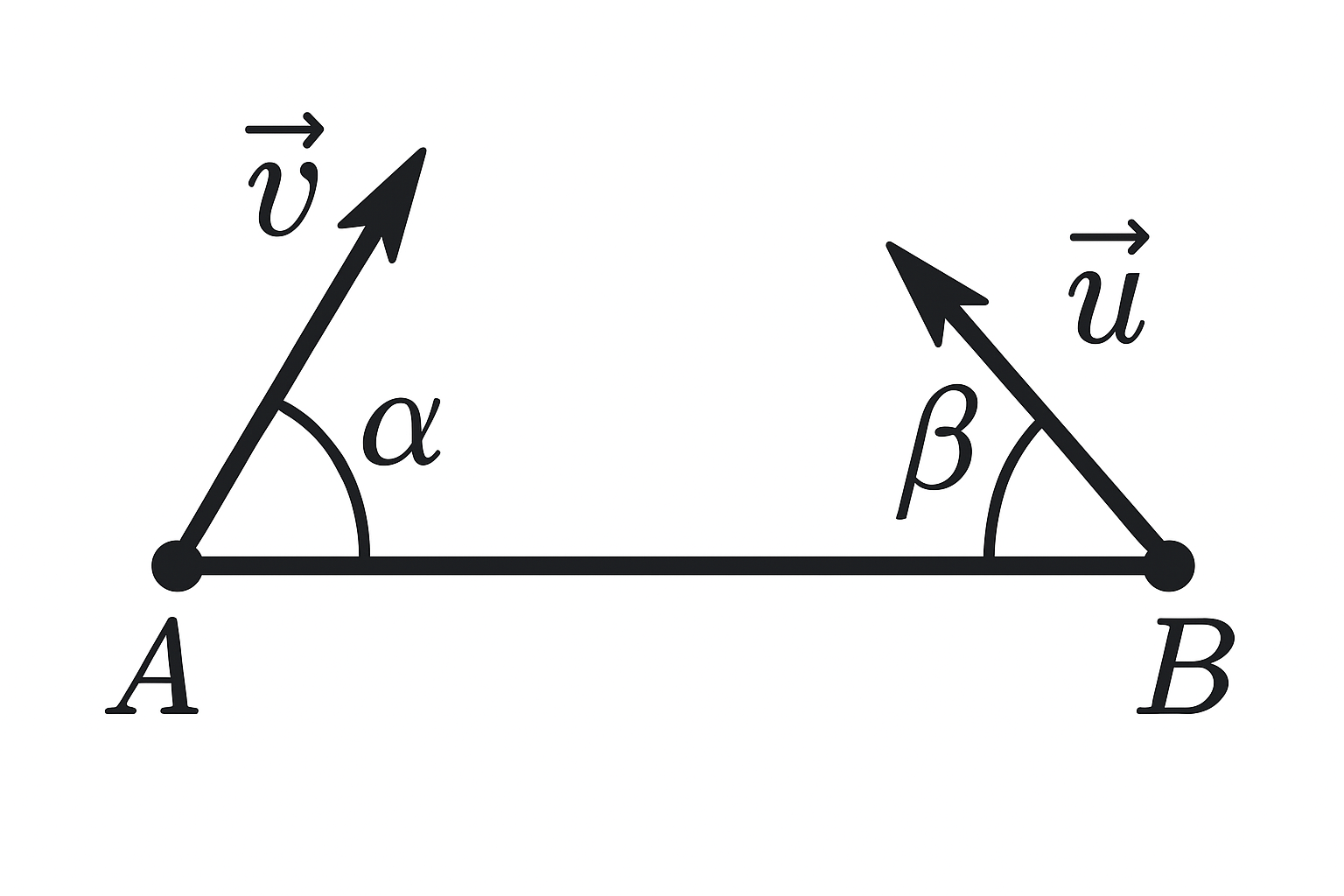
Answer
$\beta = \arcsin(\dfrac{v}{u} \sin \alpha)$.
Hint
Point C (see figure below) is the meeting place of the ship and the torpedo. $AC = vt$, $CB = ut$, where $t$ is the travel time of the torpedo. According to the sine theorem $\dfrac{AC}{\sin \beta} = \dfrac{BC}{\sin \alpha}$ or $\dfrac{vt}{\sin \beta} = \dfrac{ut}{\sin \alpha}.$ Hence $\beta = \arcsin(\dfrac{v}{u} \sin \alpha).$ 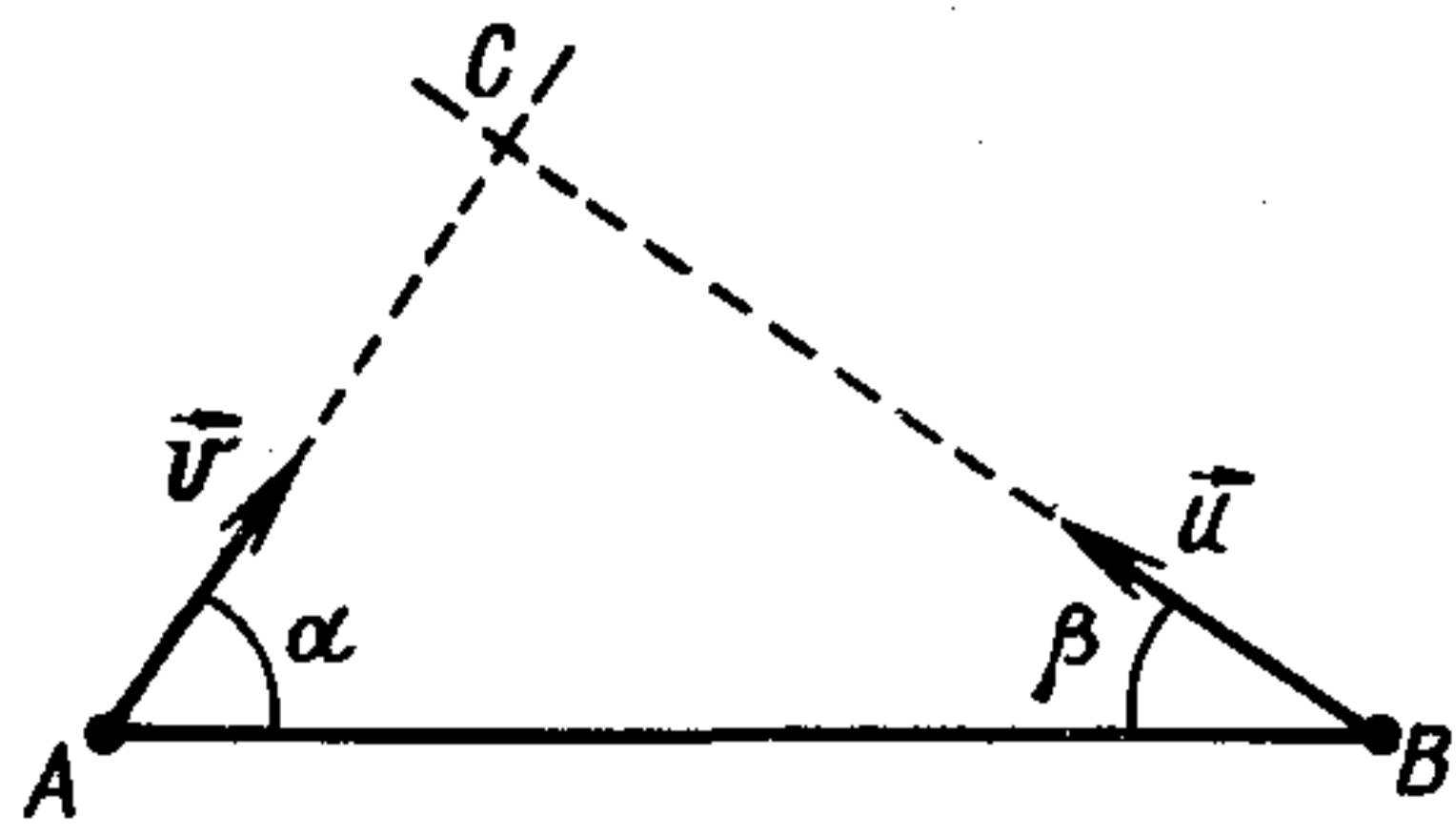
15. A cord is attached to a slider that can move along a guide rail (see figure below) and threaded through a ring. The cord is pulled at speed $v$. At what speed $u$ does the slider move when the cord makes an angle $\alpha$ with the guide rail? 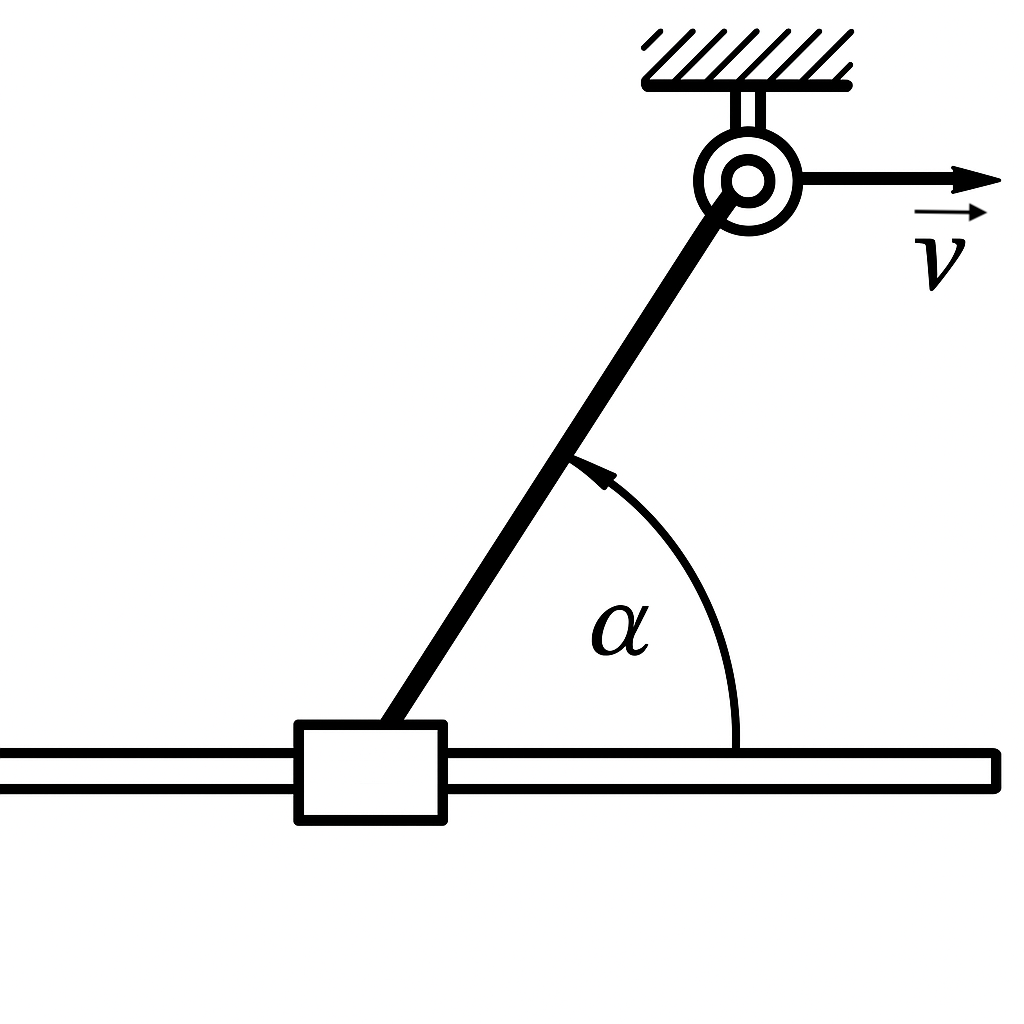
Answer
$u = v / \cos \alpha$.
Solution
For the same small time interval $\Delta t$, the slider moves by $AB = \Delta l$, and the cord is pulled by the length $AC = \Delta l \cos \alpha$ (see figure) ($\angle BCA$ can be considered right due to the smallness of $\Delta l$). Therefore, we can write $\Delta l / u = \Delta l \cos \alpha / v$, whence $u = v / \cos \alpha$, i.e., the speed of pulling the rope is equal to the projection of the slider's velocity onto the direction of the rope.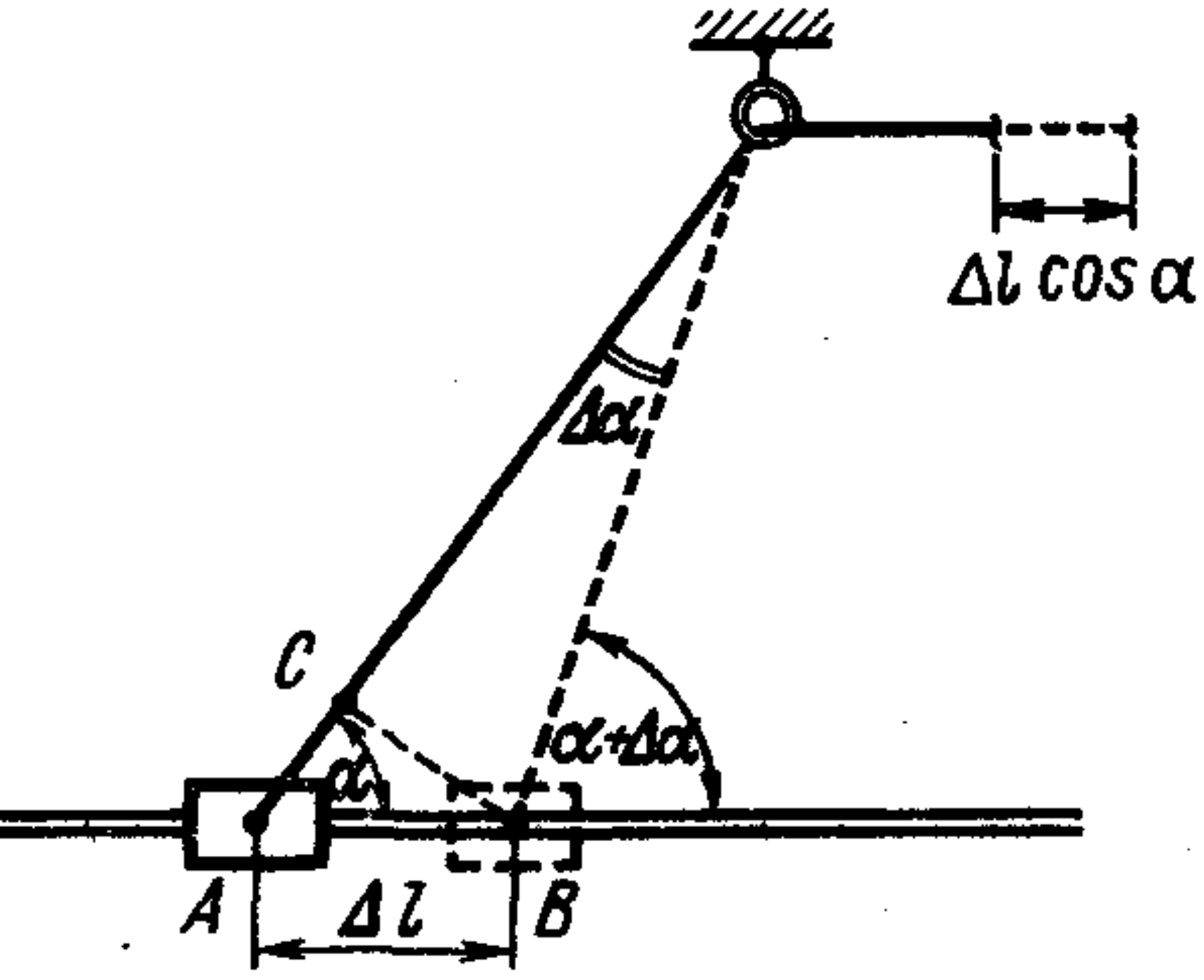
16. Workers lifting a load (following figure) pull ropes at the same speed $v$. What speed $u$ does the load have when the angle between the ropes to which it is attached is $2\alpha$? 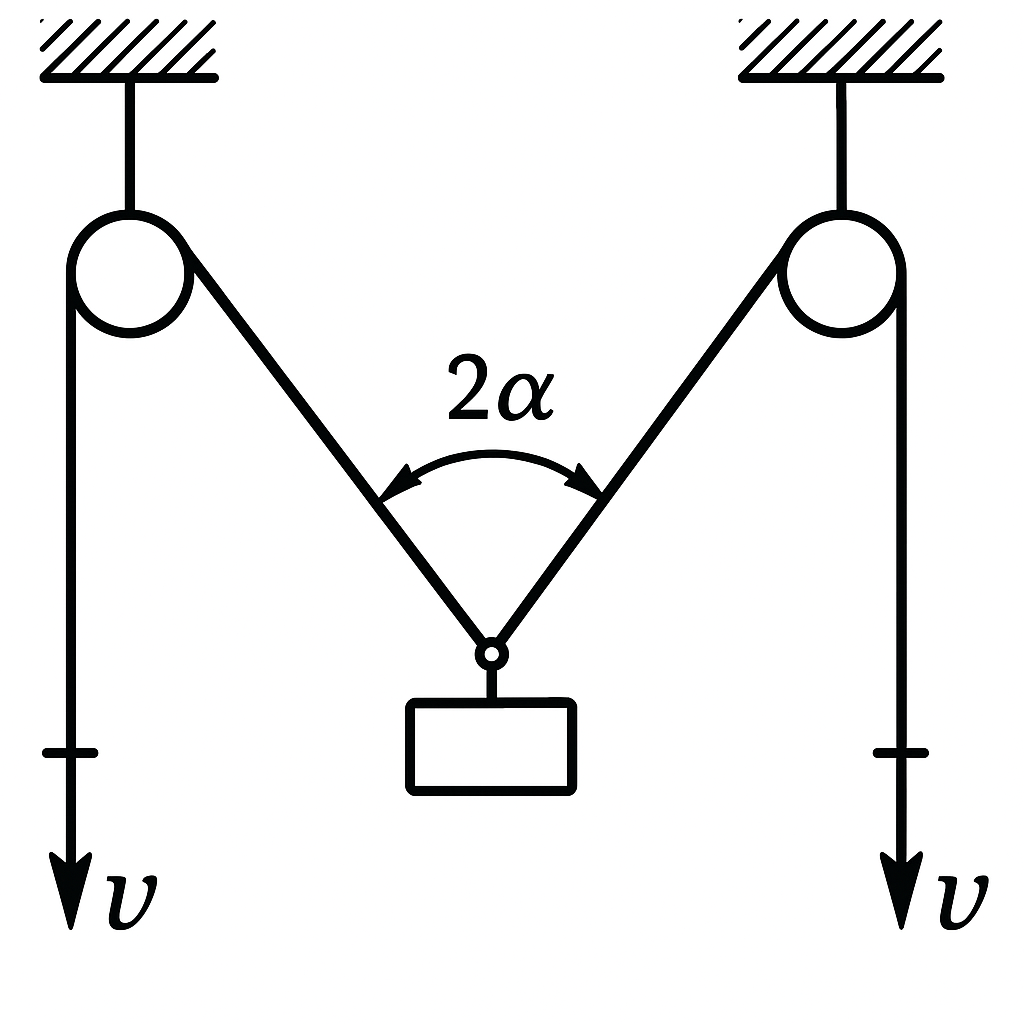
Answer
$u = v / \cos \alpha$.
Hint
The projection of the velocity $v$ of the load onto the direction of each cable must be equal to the speed $u$ of the cable (see problem 15).
17. A rod of length $l = 1\, \text{m}$ is connected by hinges to collars $A$ and $B$, which move along two mutually perpendicular rails (see figure). Collar $A$ moves at a constant speed $v_A = 30\, \text{cm/s}$. Find the speed $v_B$ of collar $B$ when the angle $OAB = 60^\circ$. Taking the time origin as when collar $A$ was at point $O$, determine the distance $OB$ and the speed of collar $B$ as a function of time. 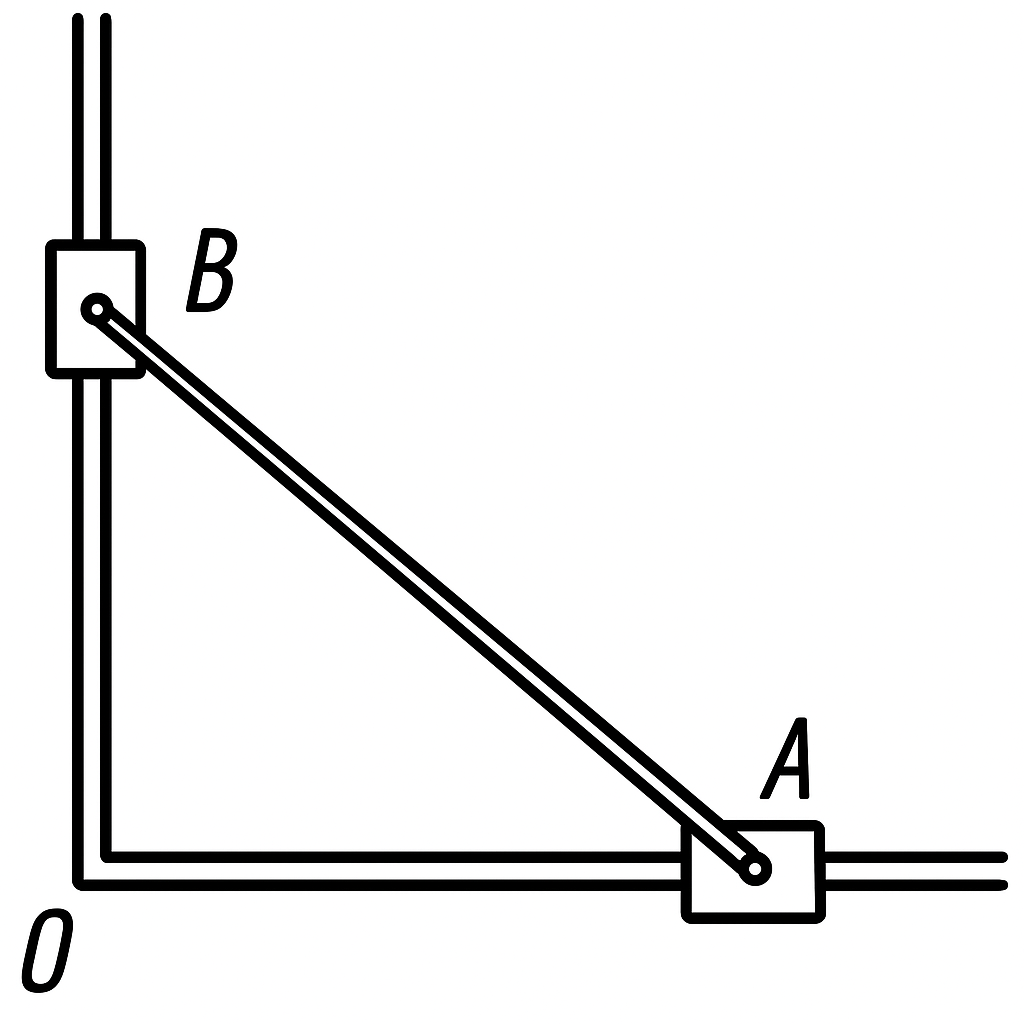
Answer
$v_B = v_A \cot \alpha = 17.3$ cm/s; $OB = \sqrt{l^2 - v_A^2 t^2}$; $v_B = v_A^2 t / \sqrt{l^2 - v_A^2 t^2}$.
Hint
See solution to problem 15. At any moment in time, the projections of the velocities $v_A$ and $v_B$ of the ends of the rod (see figure below) onto the axis of the rod are equal to each other, otherwise the rod would have to shorten or lengthen. Thus, $v_A \cos \alpha = v_B \sin \alpha$, whence $v_B = v_A \cot \alpha$. 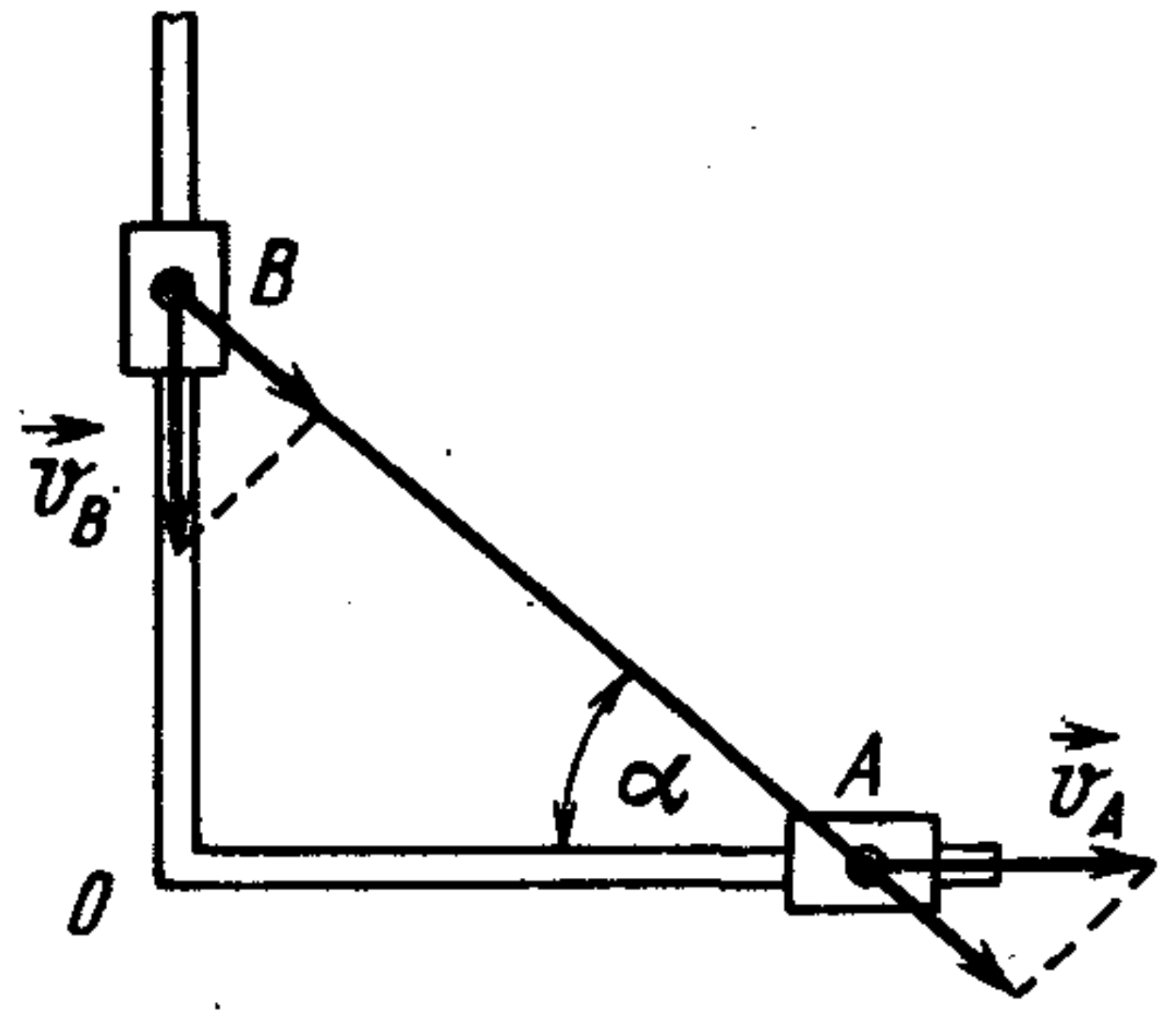
18. A tank moves at $72\, \text{km/h}$. At what speed do the following move relative to the Earth: a) the upper part of the track;
b) the lower part of the track;
c) the point on the track moving vertically relative to the tank at that moment?
Answer
a) 40 m/s;
b) 0;
c) $20\sqrt{2}$ m/s.
Hint
The velocity of any point on the track relative to the Earth at any given moment is composed of the velocity of the tank relative to the Earth and the velocity of the track link relative to the tank.
19. 1. A car travels the first half of the path at $v_1 = 40\, \text{km/h}$ and the second half at $v_2 = 60\, \text{km/h}$. Find the average speed over the entire path. 2. A car travels half the path at $v_1 = 60\, \text{km/h}$, then half the remaining time at $v_2 = 15\, \text{km/h}$, and the last segment at $v_3 = 45\, \text{km/h}$. Find the car's average speed over the entire path.
Answer
1. $v_{\text{avg}} = \dfrac{2v_1 v_2}{v_1 + v_2} = 48$ km/h;
- $v_{\text{avg}} = \dfrac{2v_1(v_2+v_3)}{2v_1 + v_2 + v_3} = 40$ km/h.
Solution
- The average speed $v_{\text{avg}}$ is numerically equal to the ratio of the total path traveled by the body to the time of motion: $v_{\text{avg}} = s_{\text{total}}/t.$ Time $t = t_1 + t_2 = \dfrac{s/2}{v_1} + \dfrac{s/2}{v_2} = \dfrac{s(v_1+v_2)}{2v_1 v_2},$ therefore $v_{\text{avg}} = s/t = \dfrac{2v_1 v_2}{v_1 + v_2}.$
2.Hint. The car traveled the second half of the path with an average speed equal to $(v_2+v_3)/2$.
20. A train travels the first half of the path at a speed $n = 1.5$ times greater than the second half. Its average speed over the entire path is $v_{\text{avg}} = 43.2\, \text{km/h}$. What are the train's speeds $v_1$ and $v_2$ for the first and second halves of the path?
Answer
$v_1 = v_{\text{avg}} \dfrac{n+1}{2} = 54$ km/h; $v_2 = v_{\text{avg}} \dfrac{n+1}{2n} = 36$ km/h.
21. Two balls start moving simultaneously with the same speed along surfaces shaped as shown in the following figure. How will their speeds and travel times differ when they arrive at point $B$? Neglect friction. 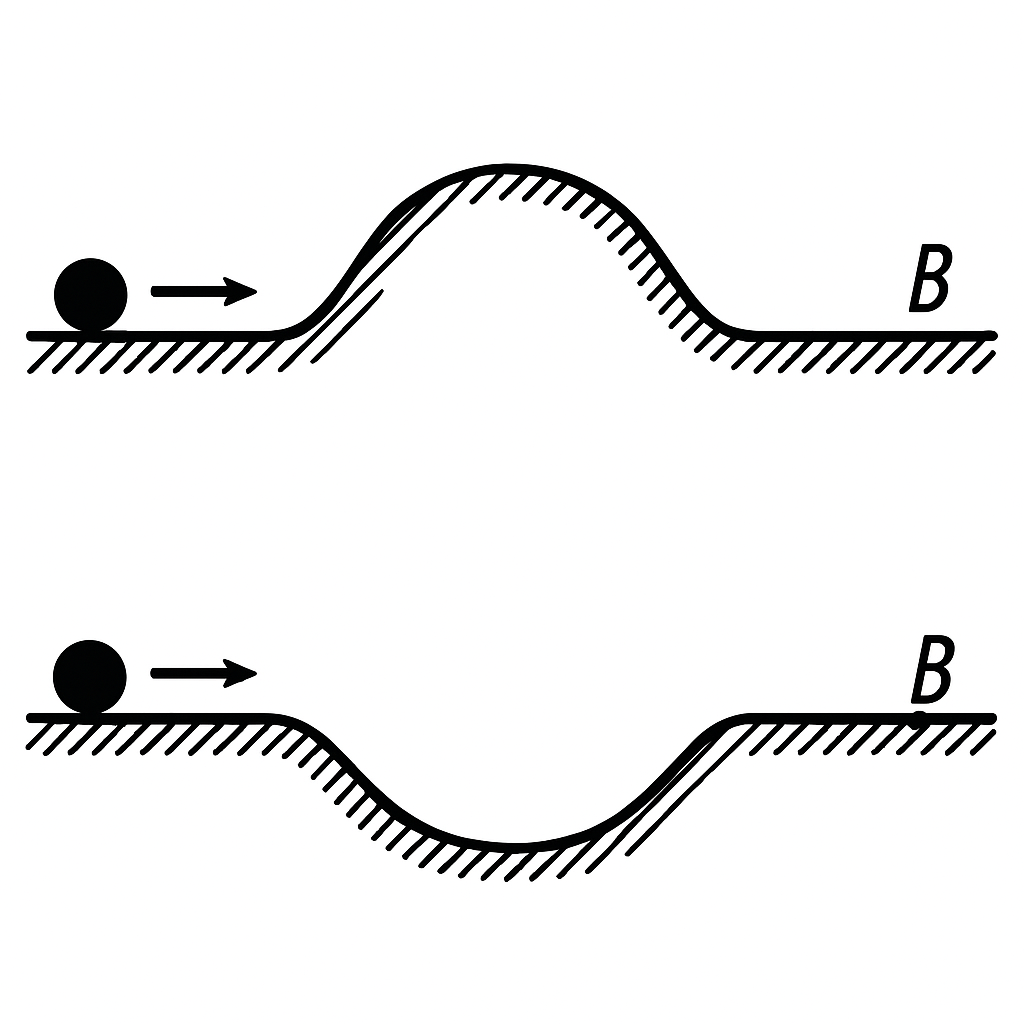
Answer
The speeds will be the same. The travel time of the second ball is less.
Solution
Sample graphs of the speed of the balls are shown in the following figure. Since the paths traveled by the balls are equal, as seen from the graph (on the graph, the path is numerically equal to the areas of the shaded figures), $t_2 < t_1$. 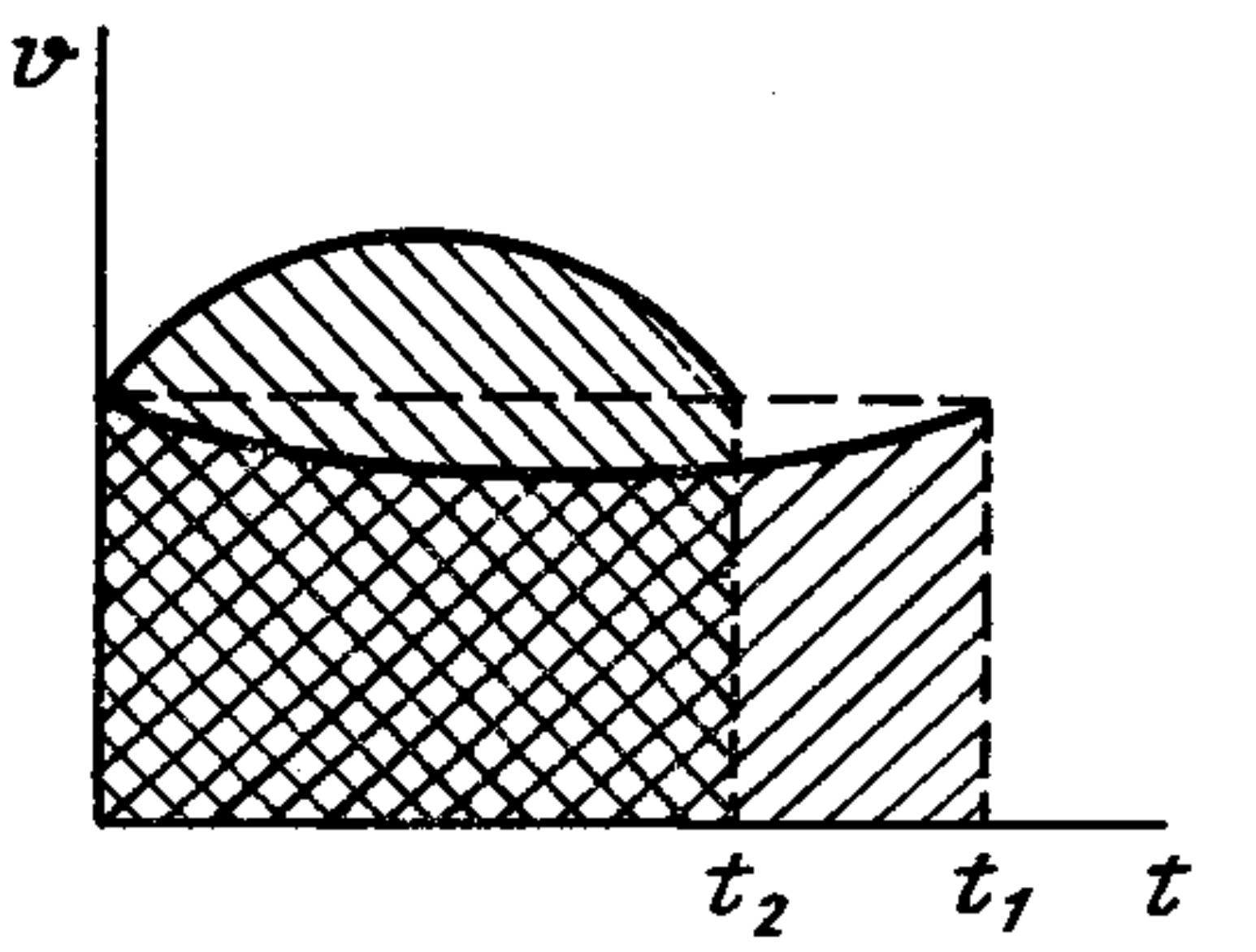
22. An airplane flies from point $A$ to point $B$ and back. Its speed in calm weather is $v$. Find the ratio of the average speeds for the entire flight in two cases: a) when the wind blows along the line $AB$; b) when the wind blows perpendicular to $AB$. The wind speed is $u$.
Answer
$\sqrt{v^2 - u^2}/v$.
Solution
If the wind blows along the line AB, the total flight time is $t_1 = \dfrac{l}{v+u} + \dfrac{l}{v-u} = \dfrac{2l v}{v^2 - u^2},$ and the average speed $v_{\text{avg}1} = \dfrac{2l}{t_1} = \dfrac{v^2 - u^2}{v}$ where $l$ is the distance between cities. If the wind is perpendicular to the line AB, the speed of the aircraft relative to the wind must be directed at an angle to the line AB, such that the drift is compensated (see figure). The flight speed in this case is constant and $v_{\text{avg}2} = \sqrt{v^2 - u^2}$ (the flight time in this case is $t_2 = 2l/\sqrt{v^2 - u^2}$). $v_{\text{avg}1}/v_{\text{avg}2} = (v^2 - u^2)/(v \sqrt{v^2 - u^2}) = \sqrt{v^2 - u^2}/v.$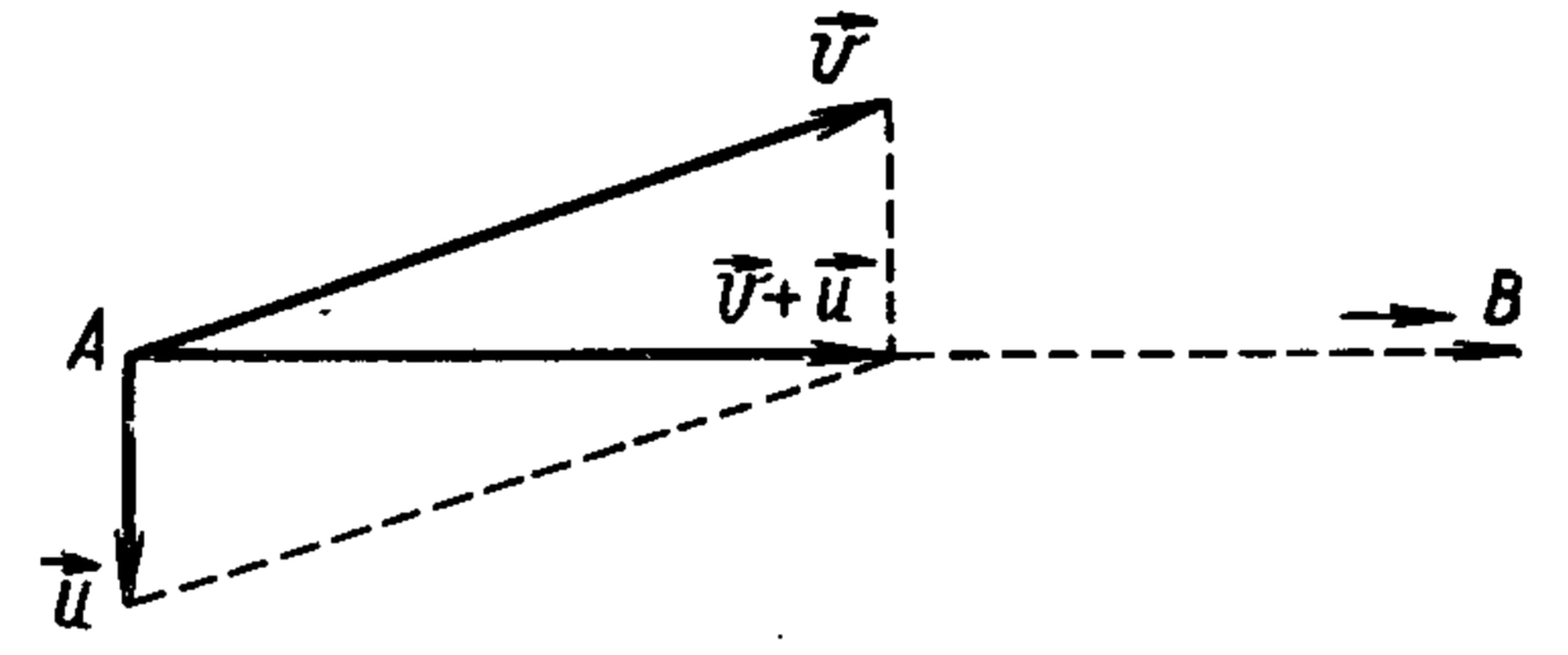
23. A metro train covers the distance $s = 3\, \text{km}$ between two stations at an average speed $v_{\text{avg}} = 54\, \text{km/h}$. It spends $t_1 = 20\, \text{s}$ accelerating, then moves uniformly for time $t_2$, and takes $t_3 = 10\, \text{s}$ decelerating to a full stop. Plot the train's speed graph and determine its maximum speed $v_{\text{max}}$.
Answer
$v_{\text{max}} \approx 16.2$ m/s. The graph of the train's speed is shown in the following figure.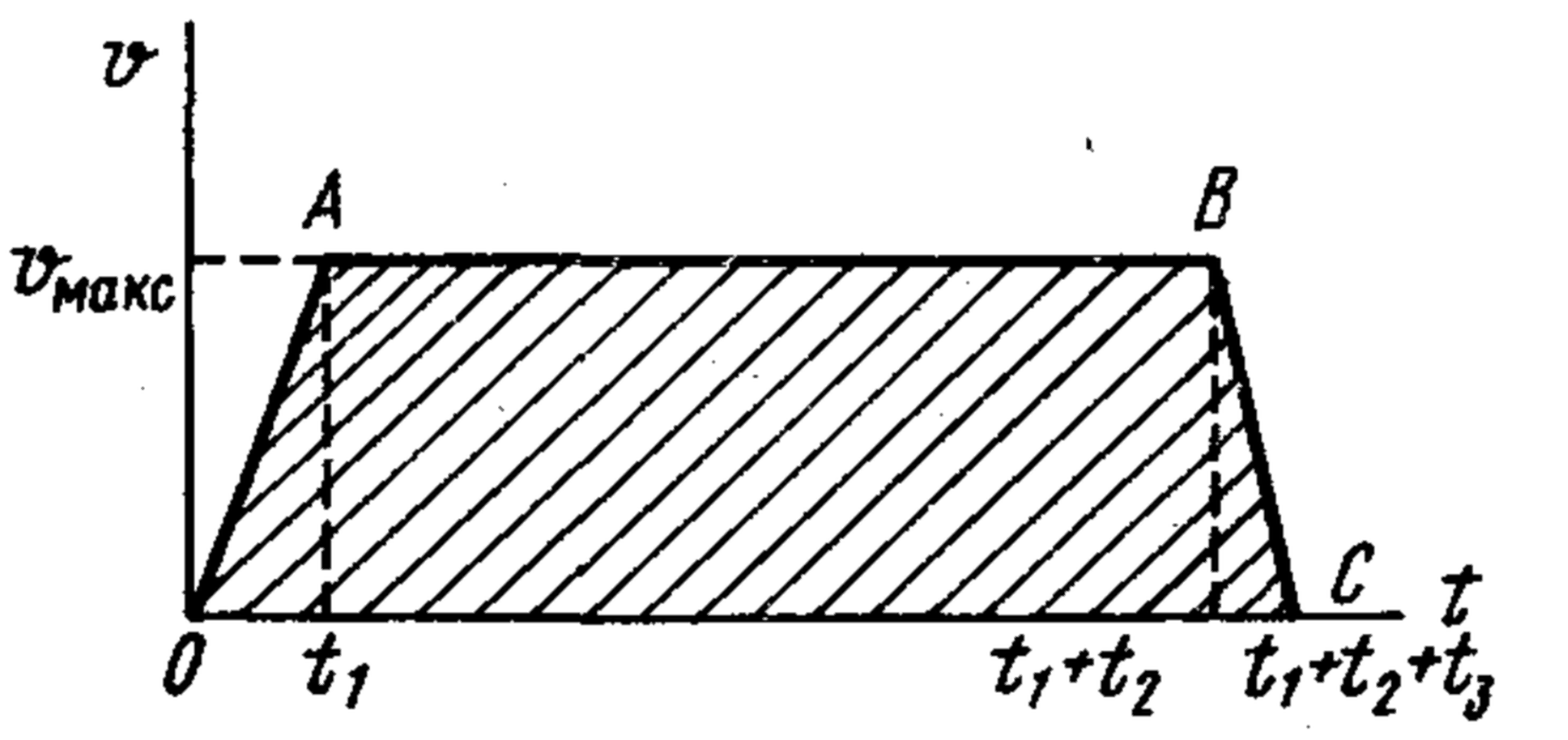
24. The last car detaches from a moving train. The train continues at the same speed $v_0$. What is the ratio of the distances traveled by the train and the car when the car stops? Assume the car decelerates uniformly. Solve the problem graphically as well.
Answer
2:1; see the following figure.
Hint
The path traveled by the train after the car was detached is equal to the area of the rectangle OABC; the path traveled by the car is the area of the triangle OAC. 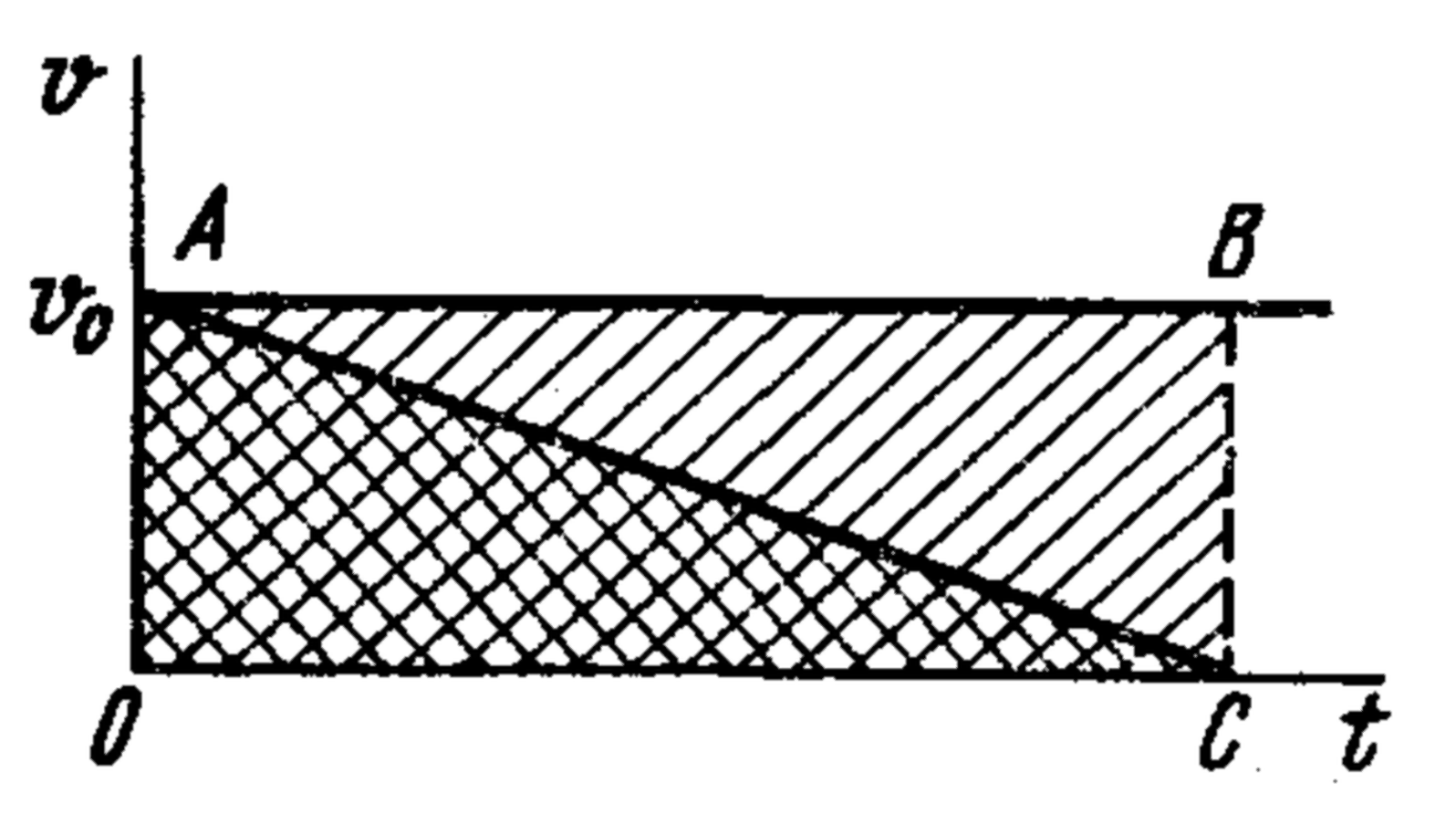
25. When the train starts moving, a well-wisher begins running uniformly alongside it at $v_0 = 3.5\, \text{m/s}$. Assuming the train's motion is uniformly accelerated, determine its speed $v$ when the well-wisher catches up.
Answer
$v = 7$ m/s; see the following figure.
Hint
From the graph, it is clear that the paths traveled by the passerby and the train are equal at the moment when $v = 2v_0$, where $v_0$ is the speed of the passerby. 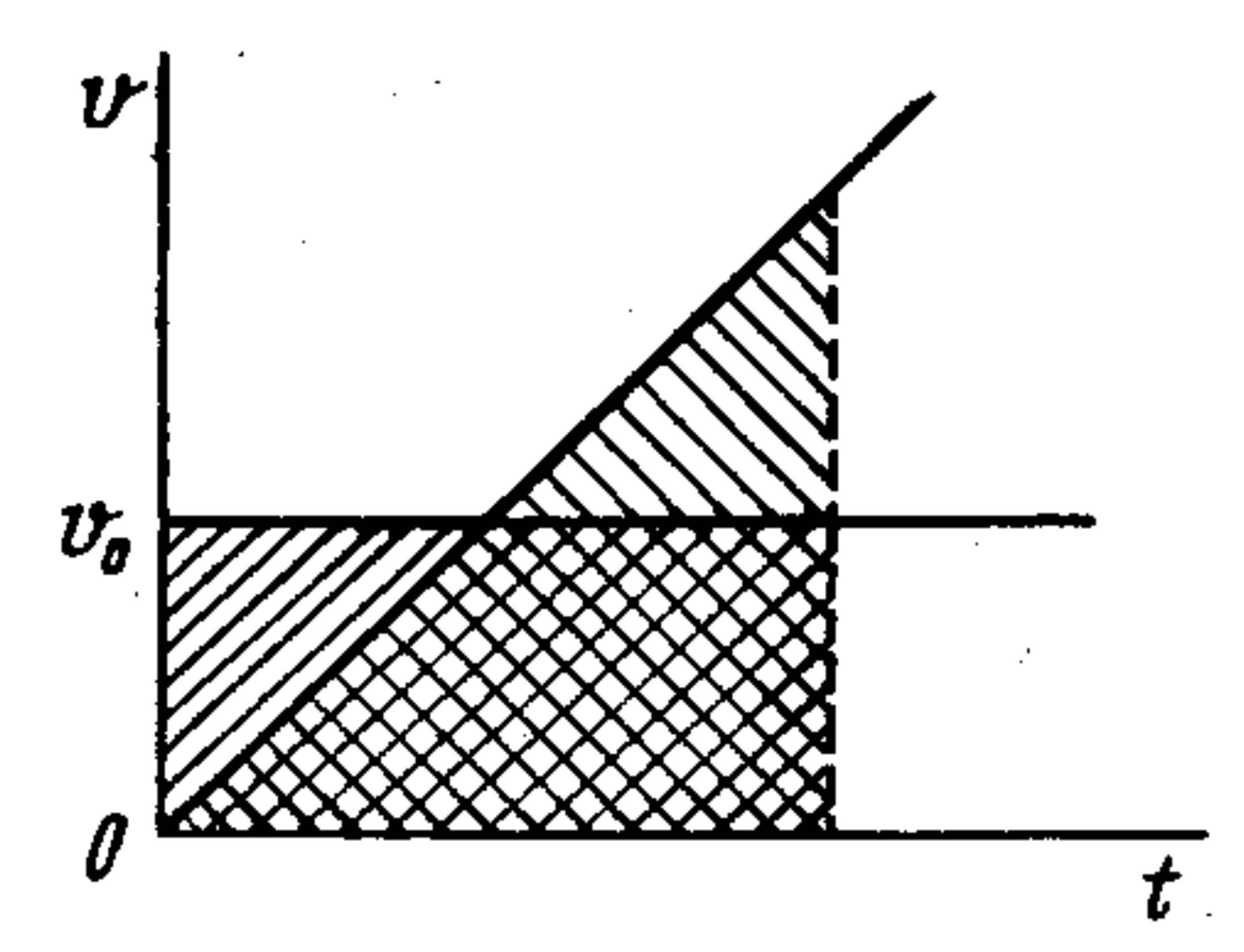
26. The graph of a body's velocity versus time is shown in the following figure. Plot the graphs of acceleration, position, and distance traveled versus time. 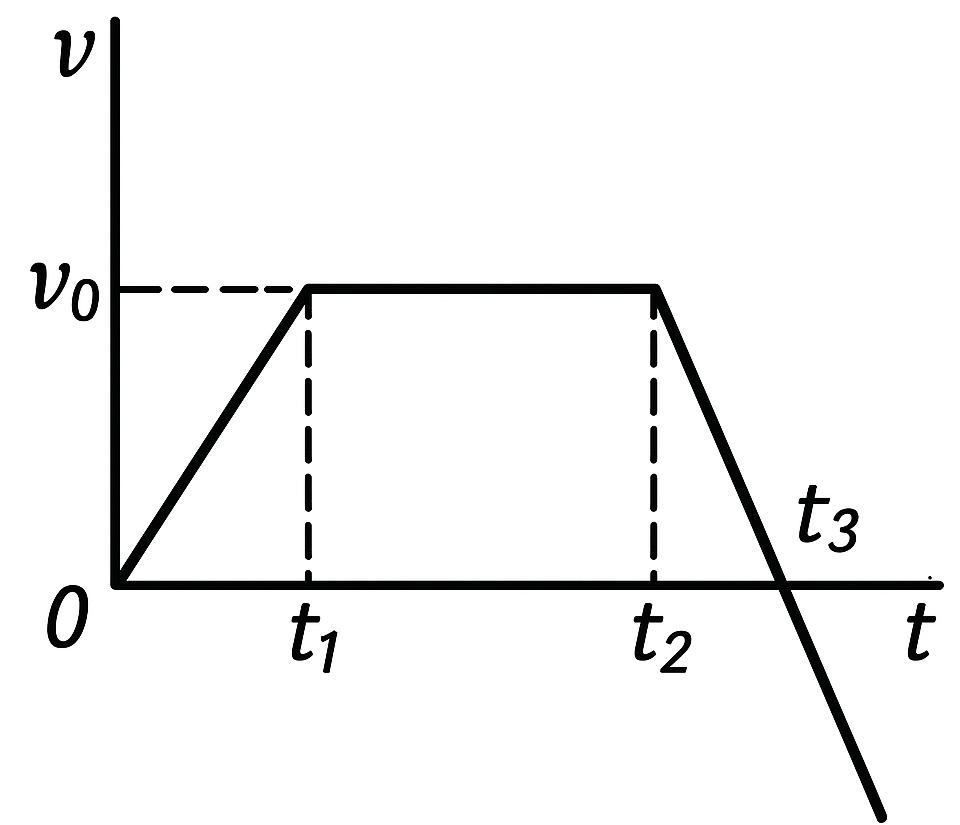
Answer
Figure below.
Hint
The tangent of the angle of inclination of the tangent to the graph of the dependence of the coordinate (or path) of the body on time is numerically equal to the speed of the body. Therefore, the straight line representing the graph $x(t)$ between $t_1$ and $t_2$ at the points corresponding to moments $t_1$ and $t_2$ will be tangent to the parabolas describing the motion of the body before moment $t_1$ and after moment $t_2$, which are the graphs $x(t)$ or $s(t)$ before moment $t_1$ and after moment $t_2$ respectively. At moments $t=0$ and $t=t_3$, the graphs $s(t)$ and $x(t)$ have a horizontal tangent. 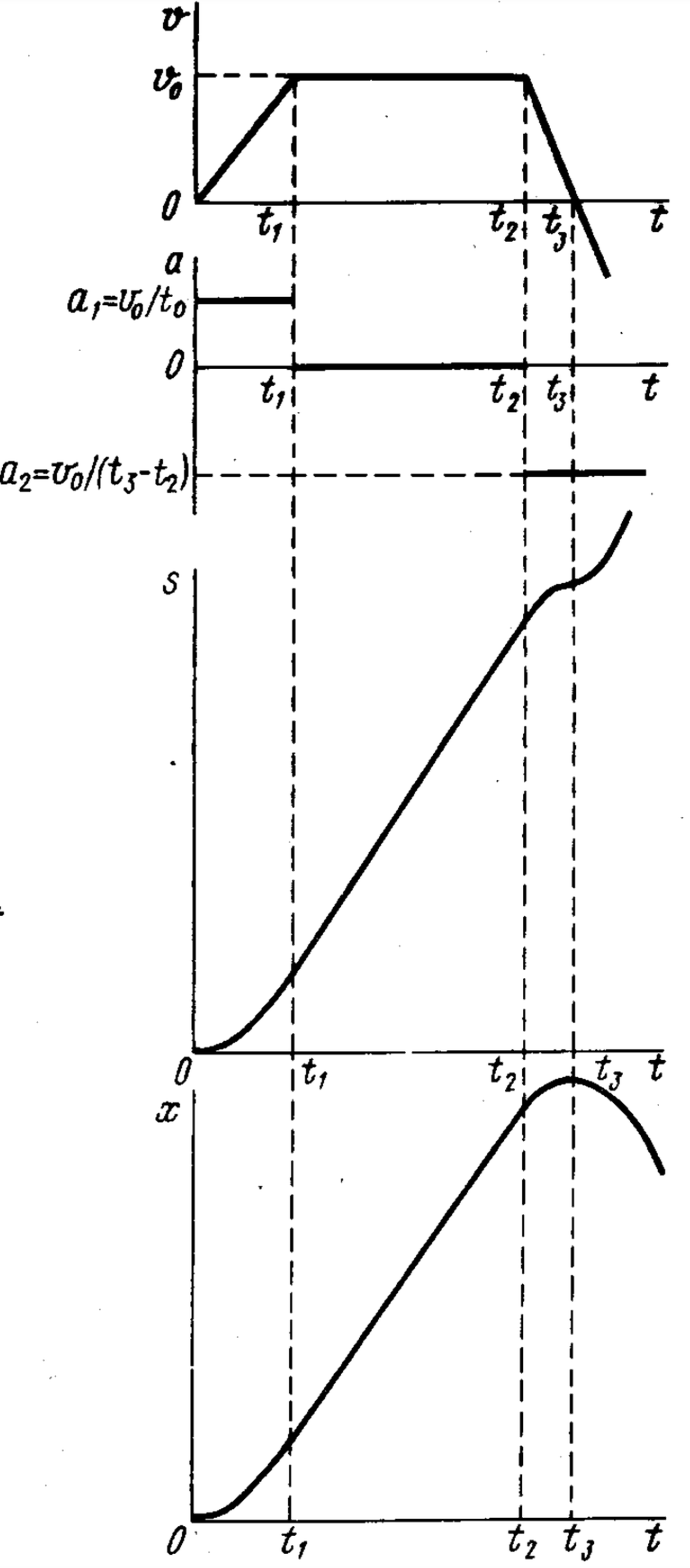
27. The graph of a body's acceleration versus time is shown in the following figure. Plot the graphs of velocity, displacement, and distance traveled versus time. The initial velocity is zero (acceleration is zero at the discontinuity). 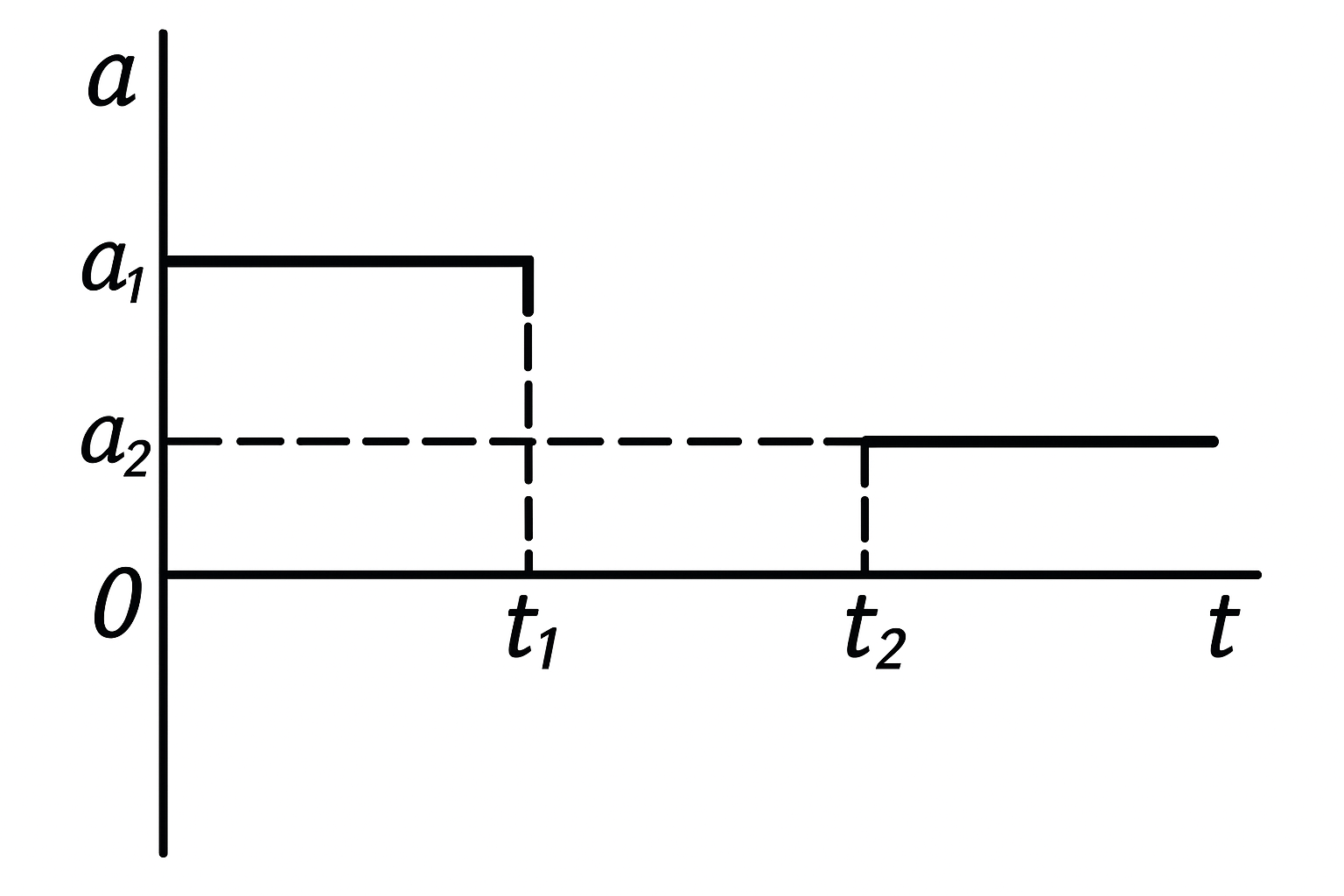
Answer
See the following figure.
Hint
The straight line between points $t_1$ and $t_2$ is tangent to the curves $x(t)$ and $s(t)$ describing the motion of the body before moment $t_1$ and after moment $t_2$. 
28. A body starts moving from point $A$ at speed $v_0$ and reaches point $B$ (see figure) after some time. What distance did the body travel if it moved with uniform acceleration $a$? The distance between $A$ and $B$ is $l$. Find the body's average speed. 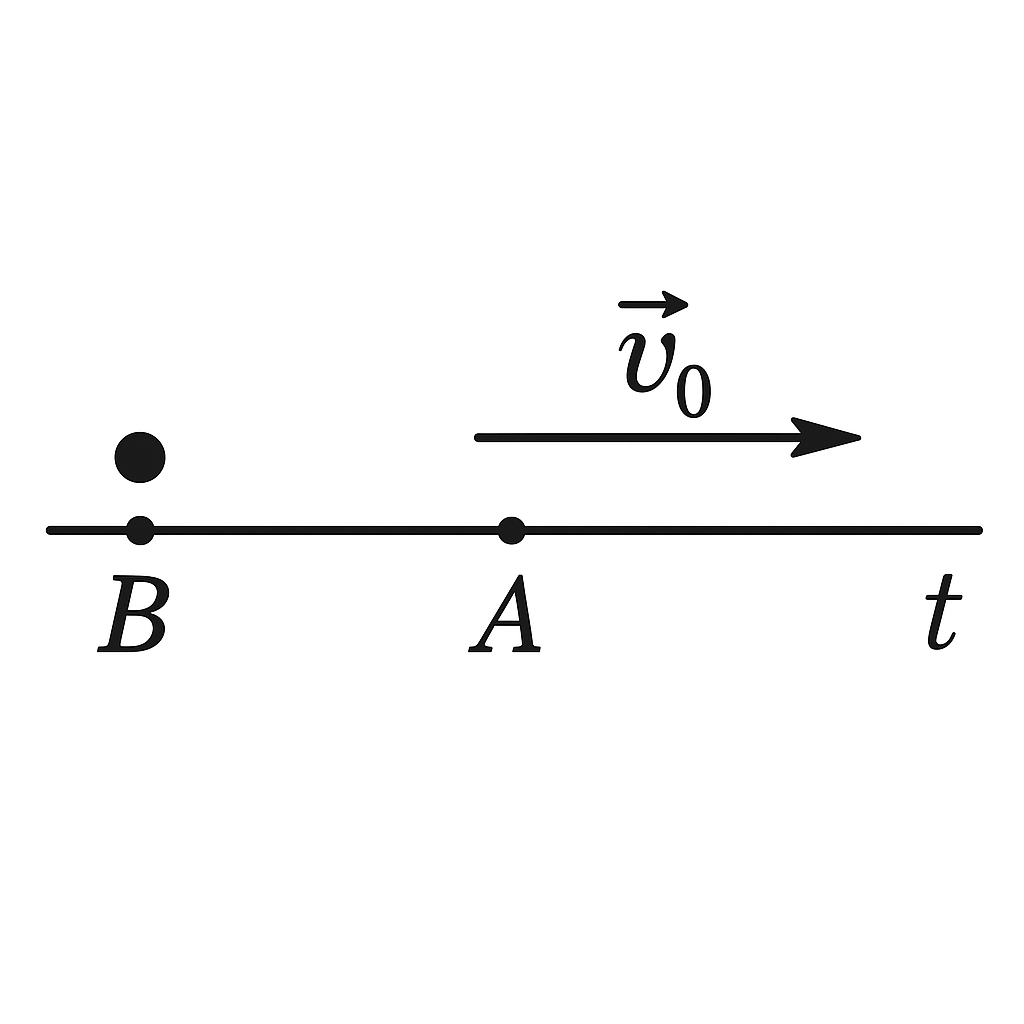
Answer
$s = \dfrac{v_0^2}{a} + l$; $v_{\text{avg}} = \dfrac{v_0^2 + al}{v_0 + \sqrt{v_0^2 + 2al}}$.
Solution
Let's introduce a coordinate system with the origin at point A and the x-axis directed along the velocity of the body at point A (see figure). When the body reaches point B, its coordinate will be $-l$. The body reaches point B only if its acceleration $a$ is directed opposite to the velocity $v_0$. Therefore, the dependence of velocity $v$ on time is expressed by the formula $v = v_0 - at$. At the moment $t_1 = v_0/a$, the velocity becomes zero. At this moment, the body is at the maximum distance from point A. For $t > t_1$, $v < 0$. Substituting $t = t_1$ into the kinematic equation of motion: $x = v_0 t - at^2/2$, we find $x_{\text{max}} = v_0^2 / (2a)$. The path $s$ traveled by the body during the entire movement is $s = 2x_{\text{max}} + l = 2\dfrac{v_0^2}{2a} + l = \dfrac{v_0^2}{a} + l.$ To find the average speed $v_{\text{avg}}$, you need to know the time of motion of the body from point A to point B. It can be found by substituting the coordinate value of point B into the equation for x, i.e., $x = -l$: $t_2 = (v_0 + \sqrt{v_0^2 + 2al})/a$ (the second root is negative, so it must be discarded). Then the average speed of the body is $v_{\text{avg}} = s/t_2 = (v_0^2 + al)/(v_0 + \sqrt{v_0^2 + 2al}).$ 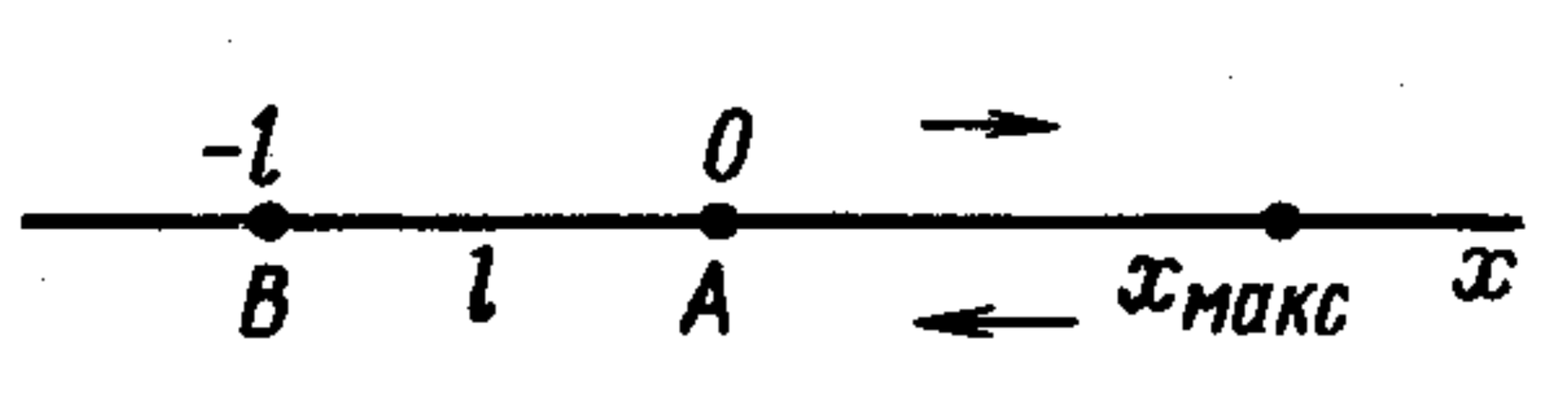
29. The following figure shows the graph of a body's position versus time. After $t = t_1$, the curve is a parabola. What motion is depicted? Plot the velocity versus time graph. 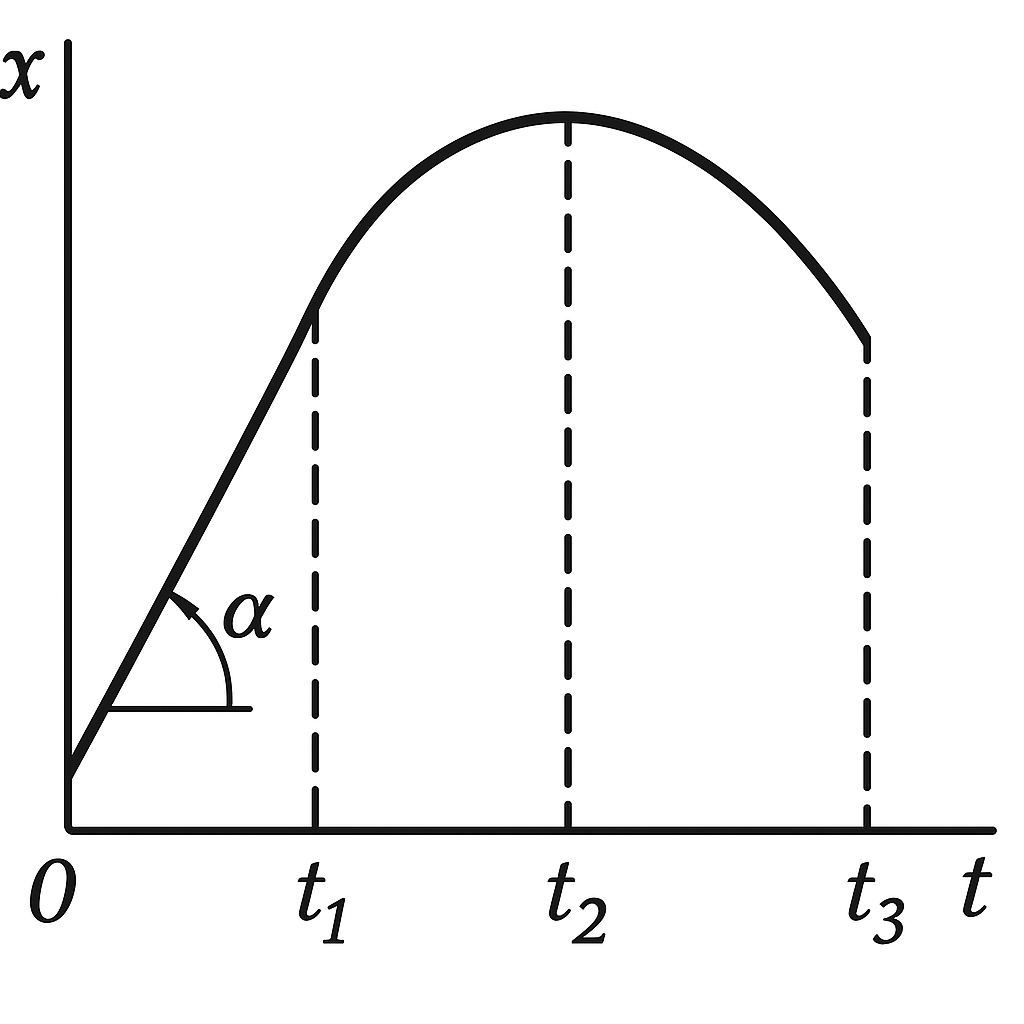
Answer
See the following; $v_1 = \tan \alpha$. Point $t_2$ corresponds to the maximum coordinate of the body. Before moment $t=t_1$, the motion is uniform, for $t > t_1$ - uniformly accelerated with negative acceleration (i.e., acceleration directed opposite to velocity $v$). 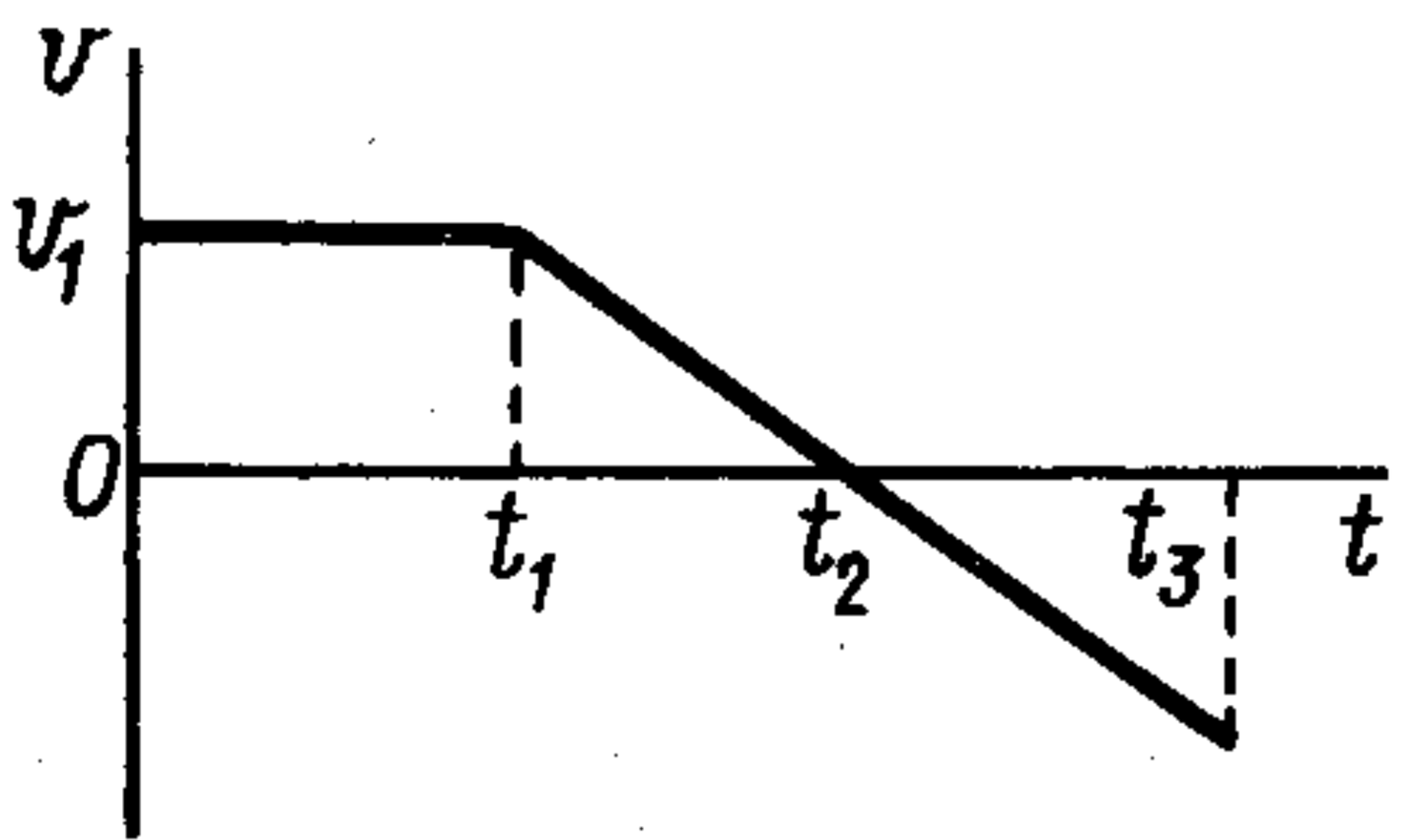
30. The following figure shows velocity graphs for two points moving along the same line from the same starting position. The times $t_1$ and $t_2$ are known. At what time $t_3$ will the points meet? Plot the motion graphs. 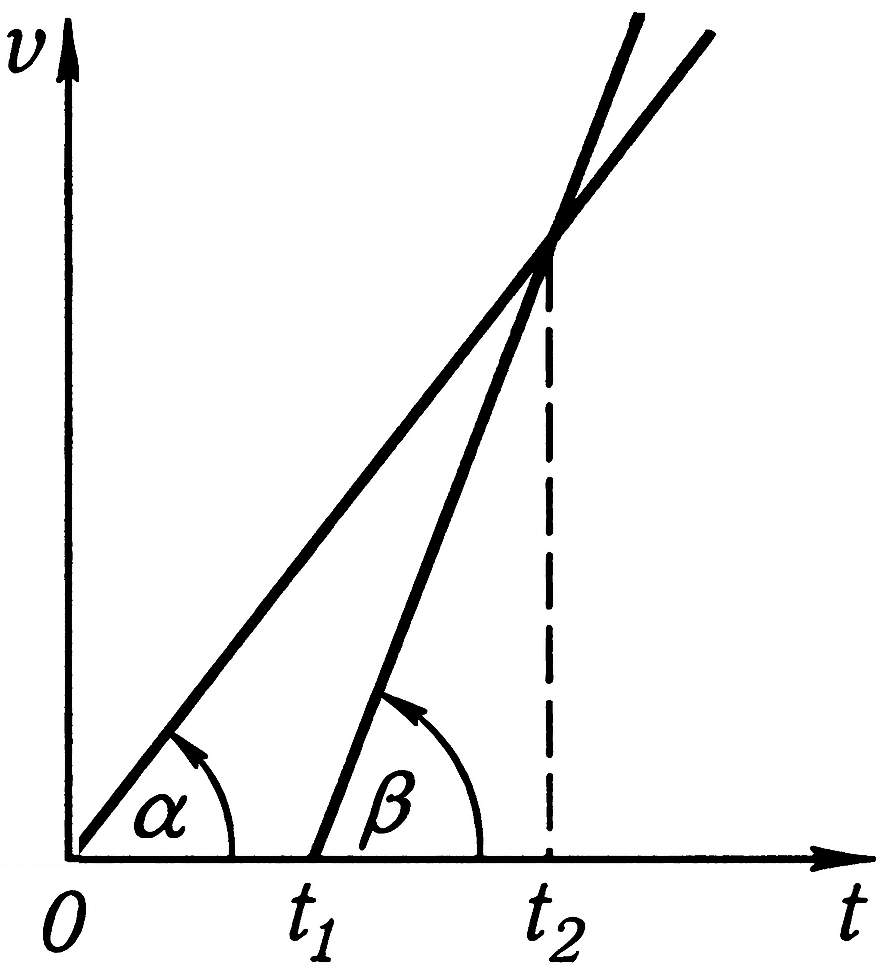
Answer
$t_3 = t_2 + \sqrt{t_2(t_2-t_1)}$.
Solution
Equating the paths traveled by the bodies by the moment $t_3$ of meeting: $a_1 t_3^2 / 2 = a_2 (t_3 - t_1)^2 / 2. \tag{1}$ From the above figure, it is clear that $a_1/a_2 = (t_2-t_1)/t_2$ ($a_1 = \tan \alpha$; $a_2 = \tan \beta$). Substituting the ratio $a_1/a_2$ into equation (1) and solving the resulting equation for $t_3$, we find $t_3 = t_2 + \sqrt{t_2(t_2-t_1)}$. The second root is discarded, as the condition $t_3 > t_2$ must be met. The graphs of motion are shown in the following.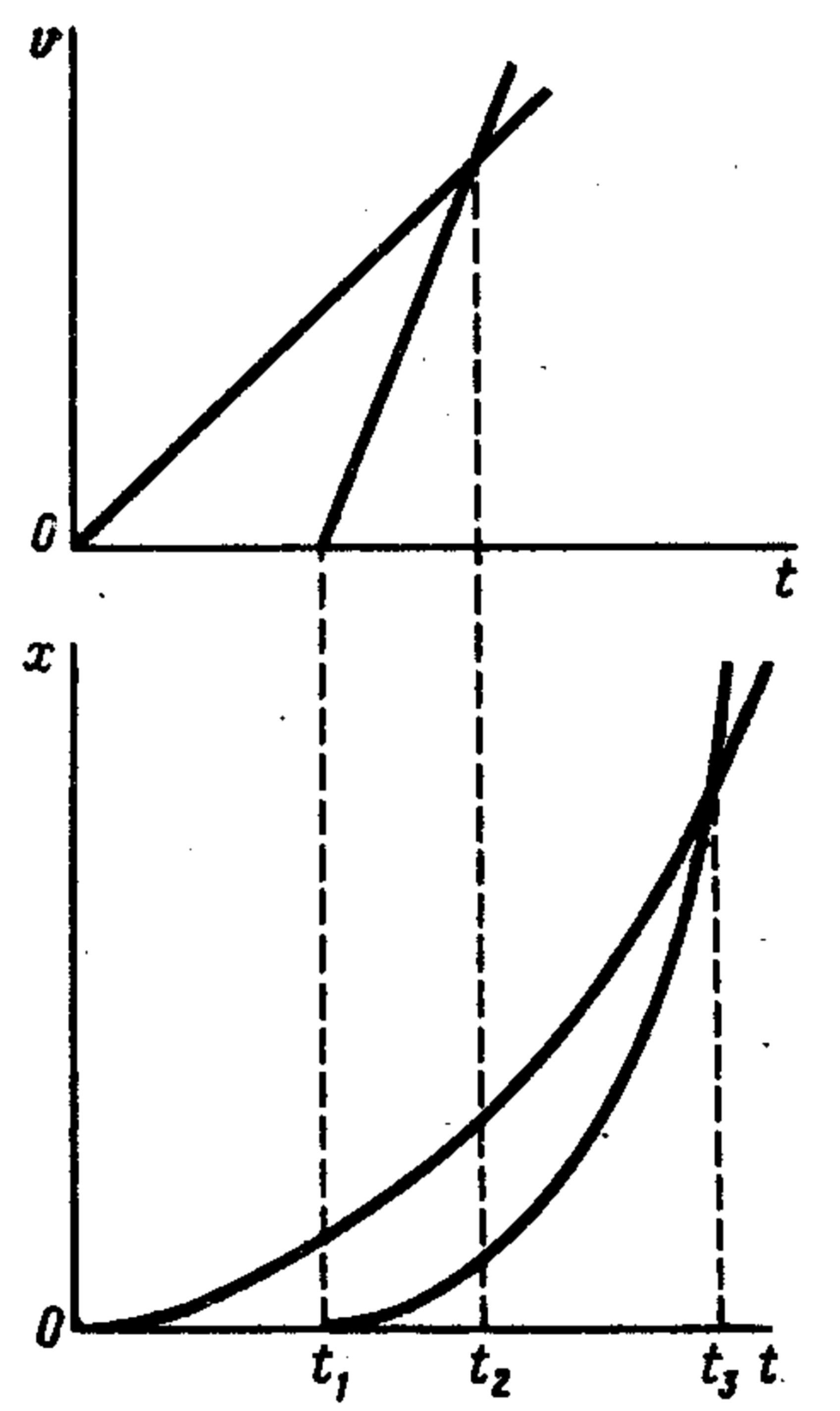
31. In uniformly accelerated motion starting from rest, during which second does the distance traveled become three times the distance traveled in the previous second?
Answer
During the second second.
32. A cart must transport cargo the shortest possible distance $L$. It can only accelerate or decelerate with constant magnitude $a$, then move uniformly or stop. What maximum speed $v$ must the cart reach to meet this requirement?
Answer
$v = \sqrt{La}$.
Solution
The time to transport the cargo will be minimum if the average speed of movement of the trolley is maximum, which is obvious. The latter, under the conditions of this problem (start and end of motion occur with constant acceleration), can only be in the case where the trolley moves the first half of the path with acceleration $+a$, and the second - with acceleration $-a$ (see figure). Thus, we can write the following relations: $v\tau/2 \cdot 2 = L/2$, $\tau/2 = v/a$, whence $v = \sqrt{La}$.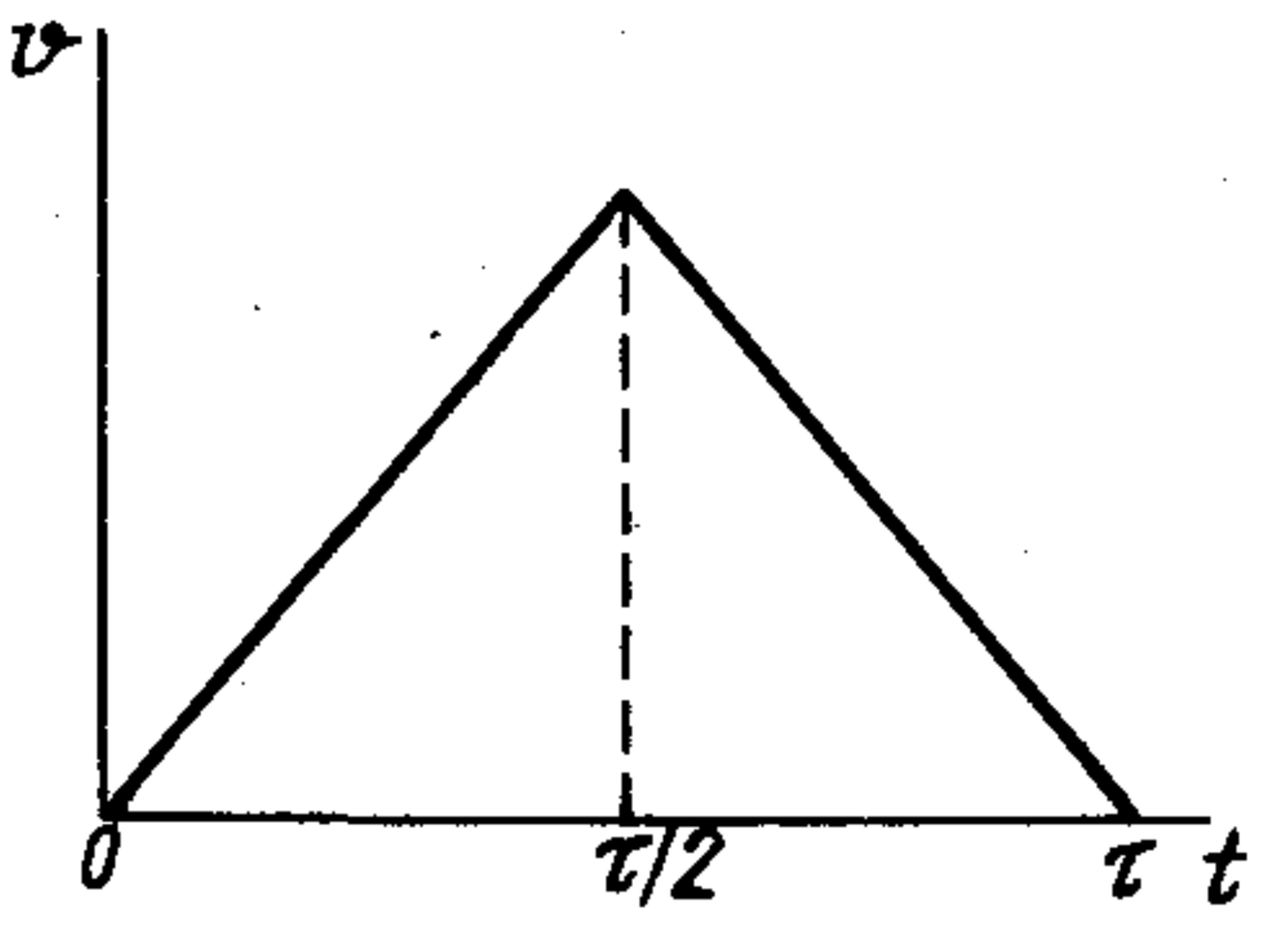
33. A jet plane flies at $v_0 = 720\, \text{km/h}$. At some point, it accelerates for $t = 10\, \text{s}$, covering $s = 295\, \text{m}$ in the last second. Determine the acceleration $a$ and final speed $v$.
Answer
$a = 10$ m/s$^2$; $v = 300$ m/s.
34. The first train car passes an observer on the platform in $t_1 = 1\, \text{s}$, and the second in $t_2 = 1.5\, \text{s}$. Each car is $l = 12\, \text{m}$ long. Find the train's acceleration $a$ and initial speed $v_0$. Assume uniformly accelerated motion.
Answer
$a = \dfrac{2l(t_1-t_2)}{t_1 t_2 (t_1+t_2)} = 3.20$ m/s$^2$; $v_0 = l/t_1 + at_1/2 \approx 13.6$ m/s.
Hint
The paths traveled by the train by moments $t_1$ and $t_1+t_2$ are respectively equal: $l = v_0 t_1 + at_1^2/2$ and $2l = v_0(t_1+t_2) + a(t_1+t_2)^2/2$.
35. A ball rolled up an inclined plane covers two equal segments of length $l$ each and continues further. The first segment takes $t$ seconds, the second $3t$ seconds. Find the ball's speed $v$ at the end of the first segment.
Answer
$v = \dfrac{5l}{6t}$.
Hint
The problem is solved most simply if we use the reversibility of motion and choose the boundary between the two segments as the origin of coordinates. Then the ball has an initial velocity - the sought value $v$, while the acceleration in the direction towards the initial point is $a$, and towards the final point is $(-a)$. Writing the equation of motion for the paths traveled by the ball, $l = vt + at^2/2$; $l = v(3t) - a(3t)^2/2$, and eliminating $a$, we find the answer.
36. A board divided into five equal segments starts sliding down an inclined plane. The first segment passes a mark on the plane in $t = 2\, \text{s}$. How long will it take for the last segment to pass the mark? Assume uniformly accelerated motion.
Answer
$\tau_n = 0.48$ s.
Solution
Let the entire length of the board be $5l$, then we can write that the time to pass the first segment is $\tau = \sqrt{2l/a}$. The times to pass the beginning and end of the n-th segment past the observer are respectively equal: $t_1 = \sqrt{\dfrac{2(n-1)l}{a}} = \tau \sqrt{n-1}$ and $t_2 = \sqrt{\dfrac{2nl}{a}} = \tau \sqrt{n},$ whence $\tau_n = t_2 - t_1 = \tau (\sqrt{n} - \sqrt{n-1}).$
37. A bullet flying at $400\, \text{m/s}$ strikes an earthen embankment and penetrates to a depth of $36\, \text{cm}$. How long did it move inside the embankment? What was its acceleration? What was its speed at a depth of $18\, \text{cm}$? At what depth did its speed reduce by a factor of three? Assume uniformly decelerated motion. What will its speed be when it has traveled 99% of its path?
Answer
$t = 1.8 \times 10^{-3}$ s; $a \approx 2.21 \times 10^5$ m/s$^2$; $v \approx 282$ m/s; $s = 32$ cm; $v_1 = 40$ m/s.
Hint
When determining at what depth the bullet's speed decreased by three times, use the formula $s = v_0^2 / (2a)$. Starting from the point where the speed decreased by three times, the remaining path will be $3^2 = 9$ times less than the total path.
38. A ball rolled up an inclined board passes a point $l = 30\, \text{cm}$ from the start twice: at $t_1 = 1\, \text{s}$ and $t_2 = 2\, \text{s}$ after starting. Determine the ball's initial speed $v_0$ and acceleration $a$, assuming it is constant.
Answer
$v_0 = 45$ cm/s; $a = 30$ cm/s$^2$.
Solution
1st method. The dependence of the coordinate of the body along the inclined plane on time is expressed by the formula $x = v_0 t - at^2/2$. Hence $t^2 - \dfrac{2v_0}{a} t + \dfrac{2x}{a} = 0.$ Since $t_1$ and $t_2$ are the roots of this equation for $x=l$, then, according to Vieta's theorem, $t_1 + t_2 = \dfrac{2v_0}{a}\quad\text{and}\quad t_1 t_2 = \dfrac{2l}{a}.$ From the obtained system of equations, it is easy to find $v_0$ and $a$.
2nd method. The dependence of the ball's speed on time is expressed by the formula $v = v_0 - at$. At time moments $t=t_1$ and $t=t_2$, the ball had speeds equal in magnitude and opposite in direction: $v_1 = -v_2$. But $v_1 = v_0 - at_1\quad\text{and}\quad v_2 = v_0 - at_2,$ therefore
$v_0 - at_1 = -v_0 + at_2,\quad\text{or}\quad 2v_0 = a(t_1+t_2).\tag{1}$
Since the ball moves with uniform acceleration, its average speed over time $t_1$ is $v_{\text{avg}1} = \dfrac{v_0+v_1}{2} = \dfrac{2v_0 - at_1}{2}.$ Therefore, $l = v_{avg1} t_1 = (2v_0 - at_1)\dfrac{t_1}{2},\quad\text{or}\quad 2v_0 - at_1 = \dfrac{2l}{t_1}.\tag{2}$
Solving equations (1) and (2) together, we find $a = \dfrac{2l}{t_1 t_2} (\dfrac{1}{t_1} + \dfrac{1}{t_2}).$
39. A body falls from a height of $100\, \text{m}$ without initial speed. How long does it take to cover the first and last meters of its path? What distance does it cover in the first and last seconds of its motion?
Answer
$t_1 \approx 0.45$ s; $t_2 \approx 0.023$ s; $s_1 \approx 4.9$ m; $s_2 \approx 40$ m.
40. Determine the open time $\tau$ of a photographic shutter if, when photographing a ball falling vertically along a centimeter scale starting from zero with no initial speed, the negative shows a streak extending from $n_1$ to $n_2$ scale divisions.
Answer
$\tau = \sqrt{2l/g}(\sqrt{n_2} - \sqrt{n_1})$.
41. A freely falling body covers the last $30\, \text{m}$ in $0.5\, \text{s}$. Find the height of the fall.
Answer
$h \approx 195$ m.
42. A freely falling body covers $1/3$ of its path in the last second. Find the fall time and height.
Answer
$t \approx 5.45$ s; $h \approx 145$ m.
Hint
Let $h$ be the height from which the body fell, and $t$ be the time of its fall from this height, we can write the following equations: $gt^2/2 = h$; $g(t-1)^2/2 = (2/3)h$. Solving them together, we get $t$ and $h$. The problem can be solved more shortly if we use the formula for the path traveled by the body in the t-th second: $s_t = \dfrac{g}{2}(2t-1);$ $\dfrac{g}{2}(2t-1) = \dfrac{1}{3} \dfrac{gt^2}{2}.$
43. With what initial speed $v_0$ must a ball be thrown downward from height $h$ to bounce up to height $2h$? Neglect air resistance and energy losses.
Answer
$v_0 = \sqrt{2gh}$.
44. Two drops fall from a roof eaves. Two seconds after the second drop starts falling, the distance between them is $25\, \text{m}$. What is the time interval between their departures? Neglect air resistance.
Answer
$\tau \approx 1$ s.
Hint
Let: $\tau$ be the time interval between the detachment of the 1st and 2nd drops, $t$ be the time from the moment of detachment of the 2nd drop, $d$ be the distance between the drops after time $t$ (from the moment of detachment of the 2nd drop) and considering that the drops move relative to each other uniformly, we can write the equation to determine $\tau$: $d = \dfrac{g\tau^2}{2} + g\tau t.$
45. A body is thrown vertically upward. An observer notes a time interval $t_0$ between two moments when the body passes point $B$ at height $h$. Find the initial speed $v_0$ and total motion time $t$.
Answer
$v_0 = \dfrac{g}{2} t_0 + \dfrac{8h}{t_0}$; $t = \sqrt{t_0^2 + \dfrac{8h}{g}}$.
Hint
See problem 38. Solve the problem using another method.
46. From points $A$ and $B$, vertically aligned ($A$ above) and $l = 100\, \text{m}$ apart, two bodies are thrown simultaneously at $10\, \text{m/s}$: from $A$ downward, from $B$ upward. When and where will they meet?
Answer
5 s; 75 m below point B.
Hint
The relative speed of the bodies is constant and equal to $2v_0$. Both bodies approach each other with this speed. Therefore, the time to meeting is $l/(2v_0) = 5$ s.
47. A body is thrown upward with initial speed $v_0$. At its peak, a second body is thrown from the same point at the same speed. At what height $h$ will they meet?
Answer
$h = (3/4)h_{\text{max}} = (3/4)v_0^2/(2g)$.
Hint
The problem can be solved beautifully if you realize that the moment of meeting divides the ascent time, as well as the fall time of the bodies, into equal parts. The paths traveled by a body falling without initial velocity in successive equal time intervals relate as 1:3. Therefore, the meeting will occur at 3/4 of the height.
48. Two bodies are thrown upward from the same point at $v_0 = 19.6\, \text{m/s}$, with a time interval $\tau = 0.5\, \text{s}$. After what time $t$ and at what height $h$ will they meet?
Answer
$t = \dfrac{v_0}{g} - \dfrac{\tau}{2} = 1.75$ s; $h = \dfrac{v_0^2}{2g} - \dfrac{g\tau^2}{8} \approx 19.3$ m.
Hint
See problem 38. Solve the problem graphically as well.
49. A balloon rises vertically from Earth at $a = 2\, \text{m/s}^2$. After $\tau = 5\, \text{s}$, an object falls out. How long $t$ until it hits the ground?
Answer
$t \approx 3.4$ s.
Solution
Let's take the coordinate axis directed vertically upwards, with the origin on the Earth's surface. Then the kinematic equation of motion of the object has the form $y = y_0 + v_0 t - g\dfrac{t^2}{2},$ where $y_0 = a\tau^2/2$ and $v_0 = a\tau.$ Substituting the coordinate value of the object at the moment of fall $y=0$ into this equation, we find $t$.
50. A balloon descending at speed $u$ throws an object upward at speed $v_0$ relative to Earth. What will be the distance $l$ between them when the object reaches its peak? What is the maximum distance $l_{\text{max}}$? How long until they are level again?
Answer
$l = v_0^2 + 2uv_0 / (2g)$; $h_{\text{max}} = (u+v_0)^2 / (2g)$; $t = 2(v_0+u)/g$.
Hint
The kinematic equation of motion of the body is conveniently written in the coordinate system associated with the moving aerostat. Here $v_0+u$ is the initial velocity of the body; $g$ is the acceleration; $h_{\text{max}}$ is the coordinate of the body when the velocity of the body relative to the aerostat is zero; $t$ is its coordinate at the moment $t_1$, when its velocity $v$ relative to the Earth is zero. Since $v = v_0 - gt$, then $v=0$ at $t_1 = v_0/g$. At $t = \tau$, the coordinate of the body is zero.
51. A body at point $B$, $H = 45\, \text{m}$ above Earth, starts falling freely. Simultaneously, another body is thrown upward from point $A$, $h = 21\, \text{m}$ below $B$, at speed $v_0$. Find $v_0$ if both bodies hit the ground simultaneously. Neglect air resistance. Take $g = 10\, \text{m/s}^2$.
Answer
$v_0 = 7$ m/s.
Solution
1st method. Taking the Earth's surface as the origin, let's write the equations of motion for both bodies:
$x_1 = H - \dfrac{gt^2}{2}; \tag{1}$
$x_2 = H - h + v_0 t - \dfrac{gt^2}{2}.\tag{2}$
At the moment of landing $x_1 = x_2 = 0$. Substituting the values $x_1$ and $x_2$ into equations (1) and (2) and solving them for $v_0$, we find $v_0 = h\sqrt{\dfrac{g}{2H}}.$
2nd method. Both bodies approach each other, moving uniformly relative to each other. The initial distance between them is $h$. Therefore, the velocity $v_0$ can be found from the equation of uniform motion $v_0 = h/t$, where $t$ is the fall time of the first body from height H. Since $t = \sqrt{2H/g}$. We find $v_0 = h/\sqrt{2H/g} = h\sqrt{g/(2H)}$.
52. A body falls freely from height $h$. Simultaneously, another body is thrown downward from height $H (H > h)$. Both hit the ground simultaneously. Find the initial speed $v_0$ of the second body. Verify with $h = 10\, \text{m}$, $H = 20\, \text{m}$, and $g = 10\, \text{m/s}^2$.
Answer
$v_0 = \dfrac{H-h}{2h} \sqrt{2gh} \approx 7$ m/s.
53. A stone is thrown horizontally from a mountain slope at angle $\alpha$. What speed $v_0$ is needed for the stone to land on the mountain at distance $L$ from the peak?
Answer
$v_0 = \sqrt{\dfrac{Lg \cos^2 \alpha }{2 \sin \alpha}}$.
Solution
Writing the coordinate equations for the stone (see figure): $x = v_0 t;\quad y =\dfrac{gt^2}{2}$ and considering that at the moment of fall of the stone $x = L \cos \alpha,\quad y = L \sin \alpha,$ we get after eliminating $t$, that $v_0 = \sqrt{\dfrac{Lg \cos^2 \alpha}{2 \sin \alpha}}$.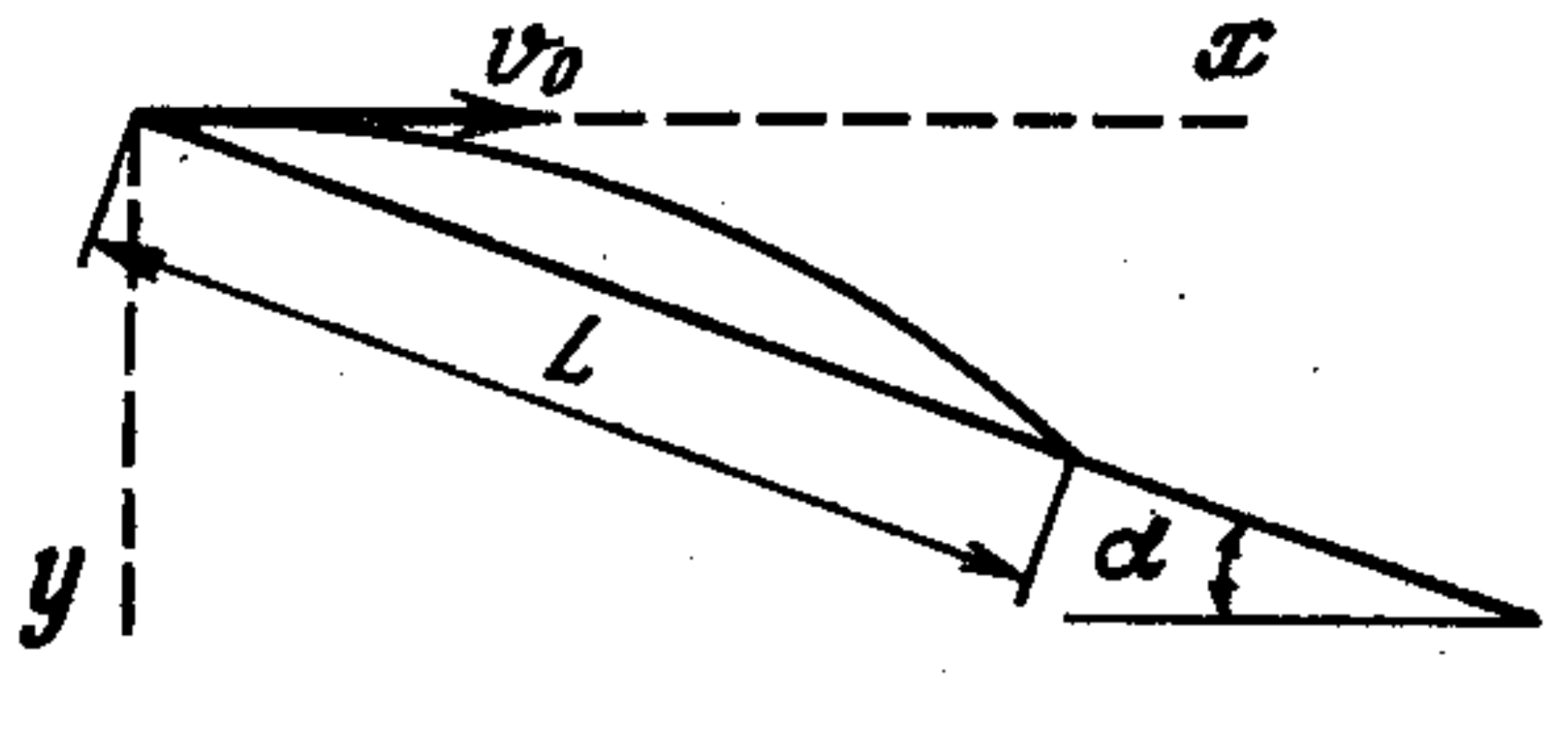
54. Two people play catch with a ball. What is the maximum height the ball reaches if it takes 2 seconds to travel from one person to the other?
Answer
4.9 m.
Hint
The ascent time of the ball is 1 s.
55. An airplane flies at constant altitude $h$ in a straight line at speed $v$. The pilot must drop a bomb on a target ahead. At what angle to the vertical must the pilot see the target at the moment of release? What is the horizontal distance from the target to the point directly below the airplane? Neglect air resistance.
Answer
$\tan \alpha = v \sqrt{2/(gh)}$; $s = v \sqrt{2h/g}$.
Hint
$\tan \alpha = s/h$ (see figure). 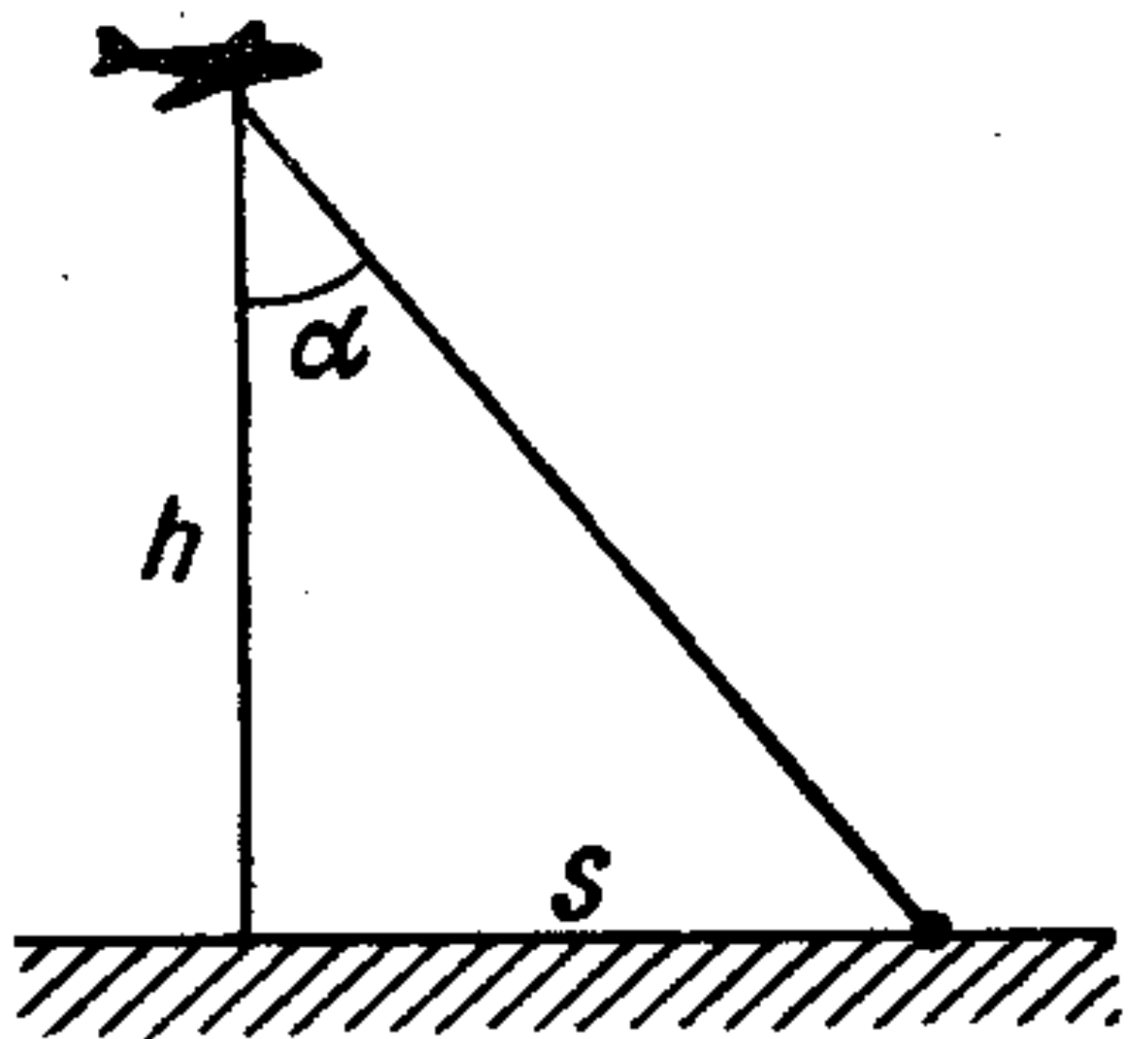
56. Two bodies fall from the same height. One encounters a platform at $45^\circ$ and rebounds elastically. How do their fall times and speeds differ?
Answer
The fall time of the first body, which did not experience a collision, is less than the fall time of the second body. The speeds of the bodies at the moments when they were at the same height are identical.
Hint
During an elastic collision, the magnitude of the velocity is conserved, only its direction changes.
57. An elevator ascends at $2\, \text{m/s}^2$. When its speed reaches $2.4\, \text{m/s}$, a bolt falls from the ceiling. The elevator is $2.47\, \text{m}$ tall. Find the bolt's fall time and distance traveled relative to the shaft.
Answer
0.64 s; 0.52 m.
Hint
In the coordinate system associated with the lift, the acceleration of the bolt is $9.8 \text{ m/s}^2 + 2 \text{ m/s}^2 = 11.8 \text{ m/s}^2$. Relative to the shaft, the initial velocity of the bolt is 2.4 m/s, and the acceleration is $9.8 \text{ m/s}^2$.
58. Two bodies are thrown simultaneously from the same height at $20\, \text{m/s}$, one downward and one upward, both at $45^\circ$ to the vertical. Find their height difference $\Delta h$ after 2 seconds. How do they move relative to each other?
Answer
$\Delta h \approx 56.4$ m; the bodies move apart with constant velocity.
Hint
In the vertical direction, both bodies move away from each other with a velocity equal to $v_0 \cos \alpha - (-v_0 \cos \alpha) = 2v_0 \cos \alpha$.
59. Prove that for freely moving bodies near Earth's surface, their relative speed is constant.
Answer
Solution
If the initial velocities of the bodies are $\vec{v}_0$ and $\vec{u}_0$, then after time $t$ their velocities are respectively $\vec{v} = \vec{v}_0 + \vec{g}t$ and $\vec{u}=\vec{u}_0+\vec{g}t$ ($\vec{g}$ is the acceleration vector of the bodies). The velocity of the second body relative to the first is $\vec{v}_{\text{rel}} = \vec{u} - \vec{v} = \vec{u}_0 - \vec{v}_0.$
60. A body falls freely from point $A$. Simultaneously, another body is thrown from point $B$ at angle $\alpha$ to the horizon so they collide mid-air (see figure). Show that $\alpha$ is independent of the initial speed $v_0$ and determine $\alpha$ if $H/l = \sqrt{3}$. Neglect air resistance. 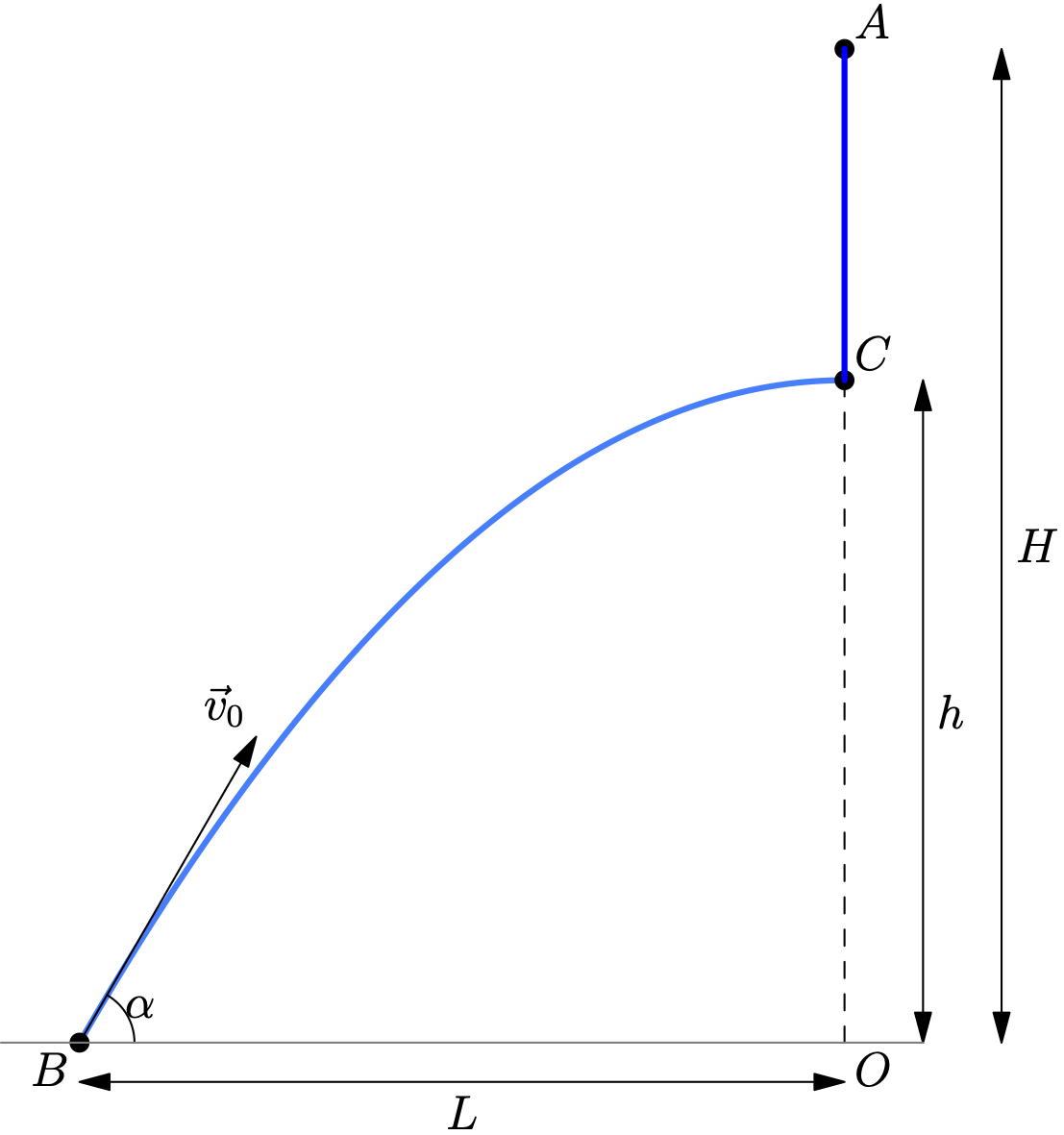
Answer
$\tan \alpha = \sqrt{3}$; $\alpha = 60^\circ$.
Solution
1st method. Both bodies can meet on the line AO (see figure above) at point C (it can also lie below the line BO).
Let's resolve the initial velocity $v_0$ of the body thrown from point B into horizontal $v_{0x}$ and vertical $v_{0y}$ components: $v_{0x} = v_0 \cos \alpha,\quad v_{0y} = v_0 \sin \alpha.$ From the start of motion until the moment of meeting, the elapsed time is: $t = l/v_{0x} = l/(v_0 \cos \alpha).\tag{1}$ During this time, body A will descend by $H-h = gt^2/2, \tag{2}$ and body B will rise to height $h = v_{0y} t - gt^2/2 = v_0 \sin \alpha t - gt^2/2. \tag{3}$ Solving equations (2) and (3) together, we find $H = t v_0 \sin \alpha. \tag{4}$ Substituting the value of $t$ from expression (1) into equation (4), we get $\tan \alpha = \dfrac{H}{l},$ i.e., the throwing angle $\alpha$ does not depend on the initial velocity, only the location of the meeting point C on the line AO depends on its value.
2nd method. Let's switch to the coordinate system associated with the body falling from point A. Here the velocity of the body thrown from point B is constant (see the previous problem). Therefore, it is clear that the bodies will meet if the velocity vector of the body is directed towards point A, i.e., $\tan \alpha = {l}. \tag{4}$
61. A body is thrown at angle $\alpha$ to the horizon with speed $v_0$. Find its speed $v$ at height $h$. Does this speed depend on $\alpha$? Neglect air resistance.
Answer
$v = \sqrt{v_0^2 - 2gh}$ and does not depend on the throwing angle.
62. A body is thrown at $\alpha = 60^\circ$ with $v = 20\, \text{m/s}$. After how long $t$ will it move at $\beta = 45^\circ$ to the horizon? Neglect friction.
Answer
$t = v (\sin \alpha - \cos \alpha \tan \beta)/g \approx 0.75$ s.
63. Water jets from three pipes on the ground have the same speed but angles $60^\circ$, $45^\circ$, and $30^\circ$ to the horizon. Find the ratios of their maximum heights $h$ and ranges $l$. Neglect air resistance.
Answer
$h_1:h_2:h_3 = 3:2:1$; $l_1:l_2:l_3 = \sqrt{3}:\sqrt{2}:1$.
Hint
Maximum ascent height $h = v_0^2 \sin^2 \alpha / (2g)$ and range of water flight $l = t v_0 \cos \alpha$, where $t$ is the time of water movement, equal to twice the ascent time to height $h$; $t = 2v_0 \sin \alpha / g$, whence $l = v_0^2 \sin 2\alpha / g$.
64. From a point at the top of a vertical diameter $d$ of a circle, weights slide without friction along chords of various inclinations (see figure below). Find the time $t$ for them to reach the circle. How does $t$ depend on the chord's angle to the vertical? 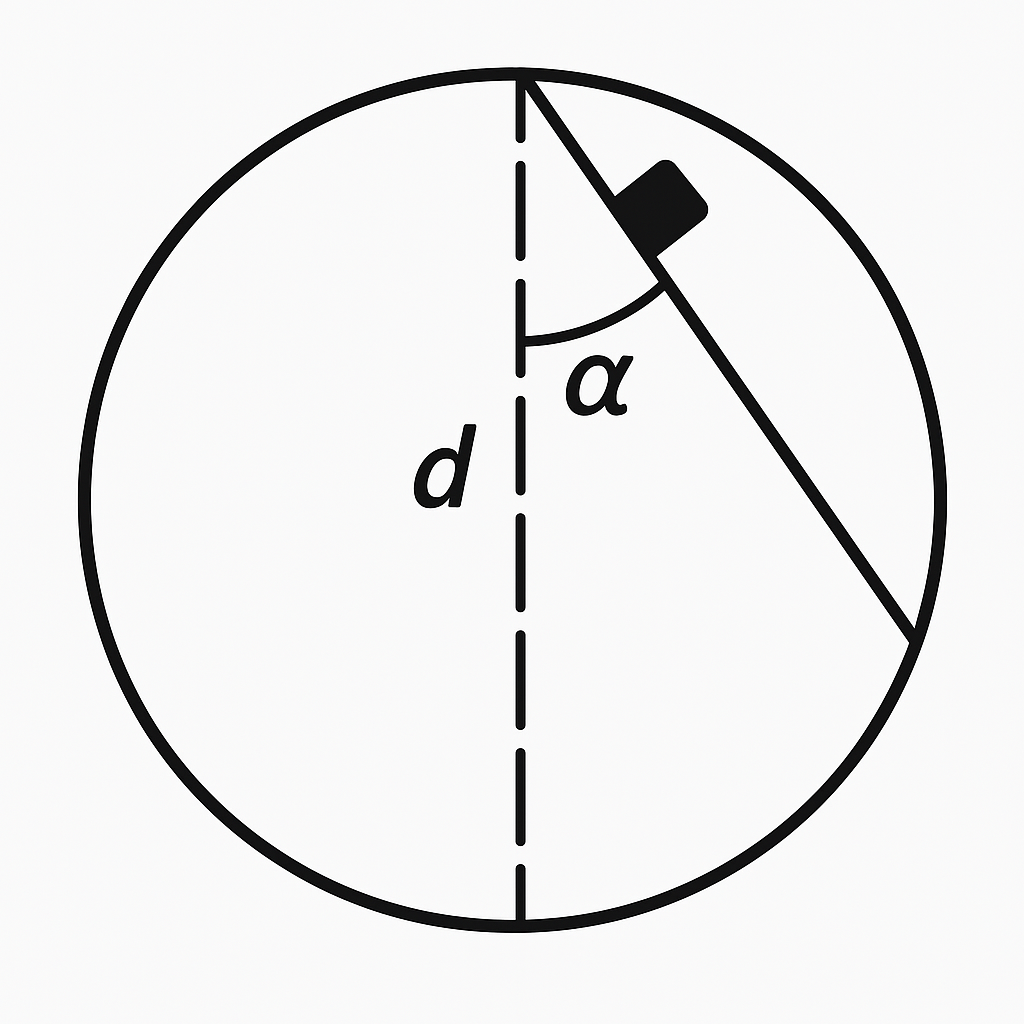
Answer
$t = \sqrt{2d/g}$; does not depend on the angle.
Solution
Along the grooves, the weights will move under the action of the component of gravity $mg \cos \alpha$ and, consequently, with acceleration $a = g \cos \alpha$; the length of the groove $l = d/\cos \alpha$ (see the above figure). The travel time $t$ of the weight is $t = \sqrt{\dfrac{2l}{a}} = \sqrt{\dfrac{2d}{g}}.$ From the formula, it is clear that $t$ does not depend on the angle.
65. A stone's initial speed is $v_0 = 10\, \text{m/s}$. After $t = 0.5\, \text{s}$, its speed is $v = 7\, \text{m/s}$. What is its maximum height above the initial level?
Answer
$H_{\text{max}} \approx 2.8$ m.
Solution
Obviously, the stone is thrown upwards at an angle, because if it were thrown vertically, its speed after 0.5 s would be $v_0 - gt = 5.1$ m/s. The height to which the stone rises, $H_{\text{max}} =\dfrac{v_{0y}^2}{2g}, \tag{1}$ where $v_{0y}$ is the vertical component of $v_0$; $v_{0y}$ can be determined from the following system of equations: $v_0^2 = v_x^2 + v_{0y}^2, \tag{2}$ $v^2 = v_x^2 + (v_{0y} - gt)^2, \tag{3}$ where $v_x$ is the horizontal projection of $v_0$. Subtracting equation (2) from equation (3), we get $v_{0y} = \dfrac{v_0^2 - v^2 + g^2 t^2}{2gt}.\tag{4}$ Substituting expression (4) into equation (1), we get $H_{\text{max}} = \dfrac{(v_0^2 - v^2 + g^2 t^2)^2}{8g^3 t^2}.$
66. Balls are thrown simultaneously from the same point at the same speed in all directions. What is the geometric locus of their positions at any time? Neglect air resistance.
Answer
A sphere with radius $v_0 t$, whose center lies below the initial point by $gt^2/2$.
Hint
As the reference body, choose a body that starts falling down from the same point at the moment the balls are thrown. Relative to it, the balls will move (disperse in possible directions) uniformly with speed $v_0$.
67. A target on a hill is visible from a cannon at angle $\alpha$ to the horizon. The horizontal distance is $L$. The cannon fires at elevation angle $\beta$ (see figure below). Find the initial speed $v_0$ to hit the target. Neglect air resistance. For what angle $\beta_0$ is the range along the slope maximized? 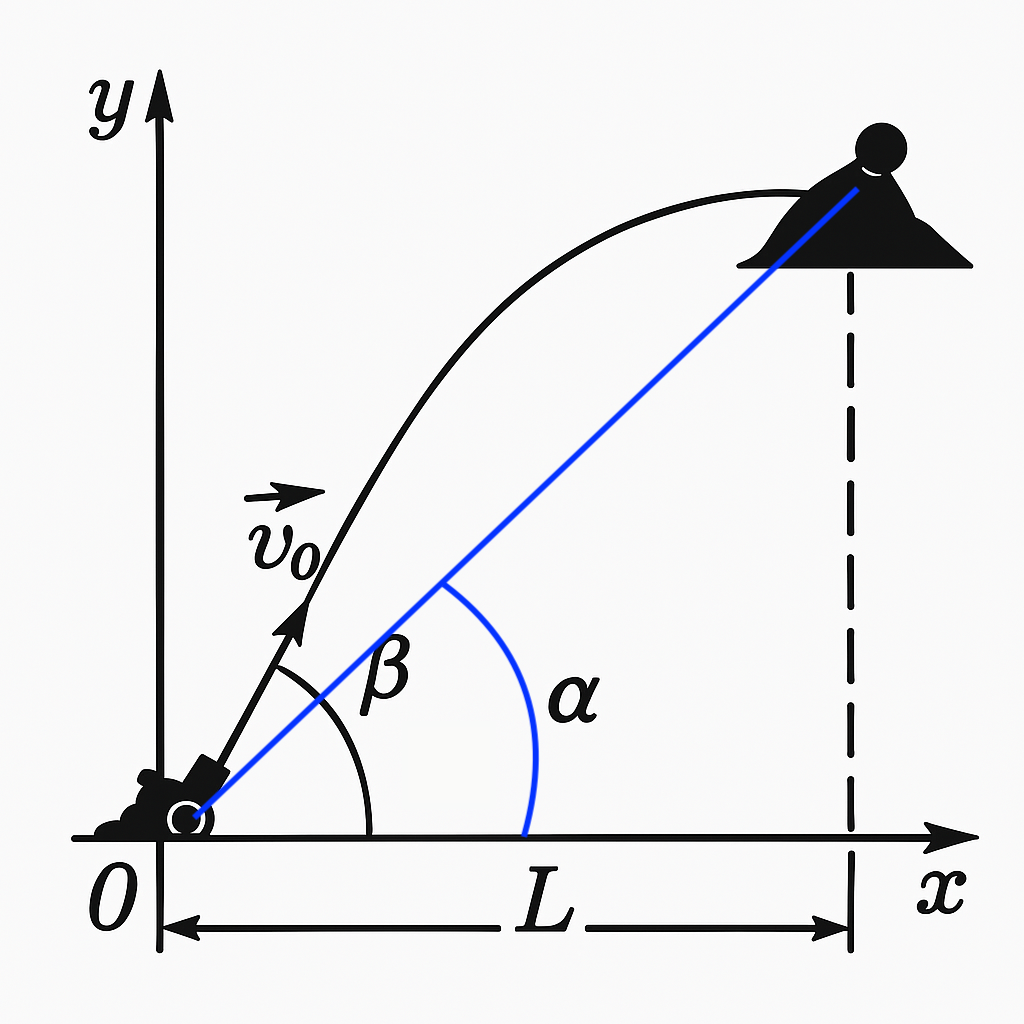
Answer
$v_0 = \sqrt{\dfrac{gL \cos \alpha}{2 \cos \beta \sin(\beta - \alpha)}}$; $\beta_0 = \dfrac{\pi}{4} + \dfrac{\alpha}{2}$.
Solution
Let's choose the coordinate $xy$ system, whose origin is at the location of the gun (see the above figure). Then the kinematic equations of motion of the projectile in coordinates x, y will be expressed as follows: $x = v_0 t \cos \beta,\quad y = v_0 t \sin \beta - gt^2/2.$ Substituting the coordinates of the target $x=L$; $y=L \tan \alpha$ into these equations, eliminating $t$, we get $v_0 = \sqrt{\dfrac{gL \cos \alpha}{2 \cos \beta \sin(\beta - \alpha)}}.$ The range $l$ of the projectile along the slope is $l = L/\cos \alpha$. Therefore, the formula we obtained can be written as: $v_0 = \sqrt{\dfrac{gl \cos^2 \alpha}{2 \cos \beta \sin(\beta - \alpha)}}.$ Hence $l = \dfrac{2 v_0^2 \cos \beta \sin(\beta - \alpha)}{g \cos^2 \alpha}.$ This expression is maximum at the maximum product $\cos \beta_0 \sin(\beta_0 - \alpha) = \dfrac{1}{2} [\sin(2\beta_0 - \alpha) - \sin \alpha].$ Therefore, $l$ is maximum at the maximum value $\sin(2\beta_0 - \alpha) = 1$ or $\beta_0 = \dfrac{\pi}{4} + \dfrac{\alpha}{2}$ (for $\alpha = 0$ we get the answer $\beta_0 = \pi/4 = 45^\circ$).
68. An elastic body falls from height $h$ onto an inclined plane. How long $t$ after bouncing will it hit the plane again? How does $t$ depend on the plane's angle?
Answer
$t = 2\sqrt{2gh}/g$; does not depend on the angle.
Solution
Let's take the coordinate system xOy, whose origin is located at the point of the first contact of the body with the inclined plane, the x-axis is directed along the inclined plane, and the $y$-axis is perpendicular to it (see figure below). With this choice of coordinate system, the solution of the problem is significantly simplified. The initial velocity $v_0$ of the body after the collision will be $v_0 = \sqrt{2gh}$ and forms an angle $\alpha$ with the $y$-axis. The equation of motion of the body along the $y$-axis will be expressed as follows: $y = v_{0y} t + a_y t^2 / 2,$ where $v_{0y} = v_0 \cos \alpha\text{ and } a_y = -g \cos \alpha$ are the projections of the velocity $v_0$ and acceleration $g$ onto the $y$-axis. At the moment the body falls onto the inclined plane $y=0$. Substituting $y=0$ into the equation written above, we get $t = 2v_{0y}/a_y = 2v_0/g = 2\sqrt{2gh}/g.$ The fall time does not depend on the angle of inclination of the plane. This time will remain unchanged for subsequent falls after the first reflection onto the inclined plane. 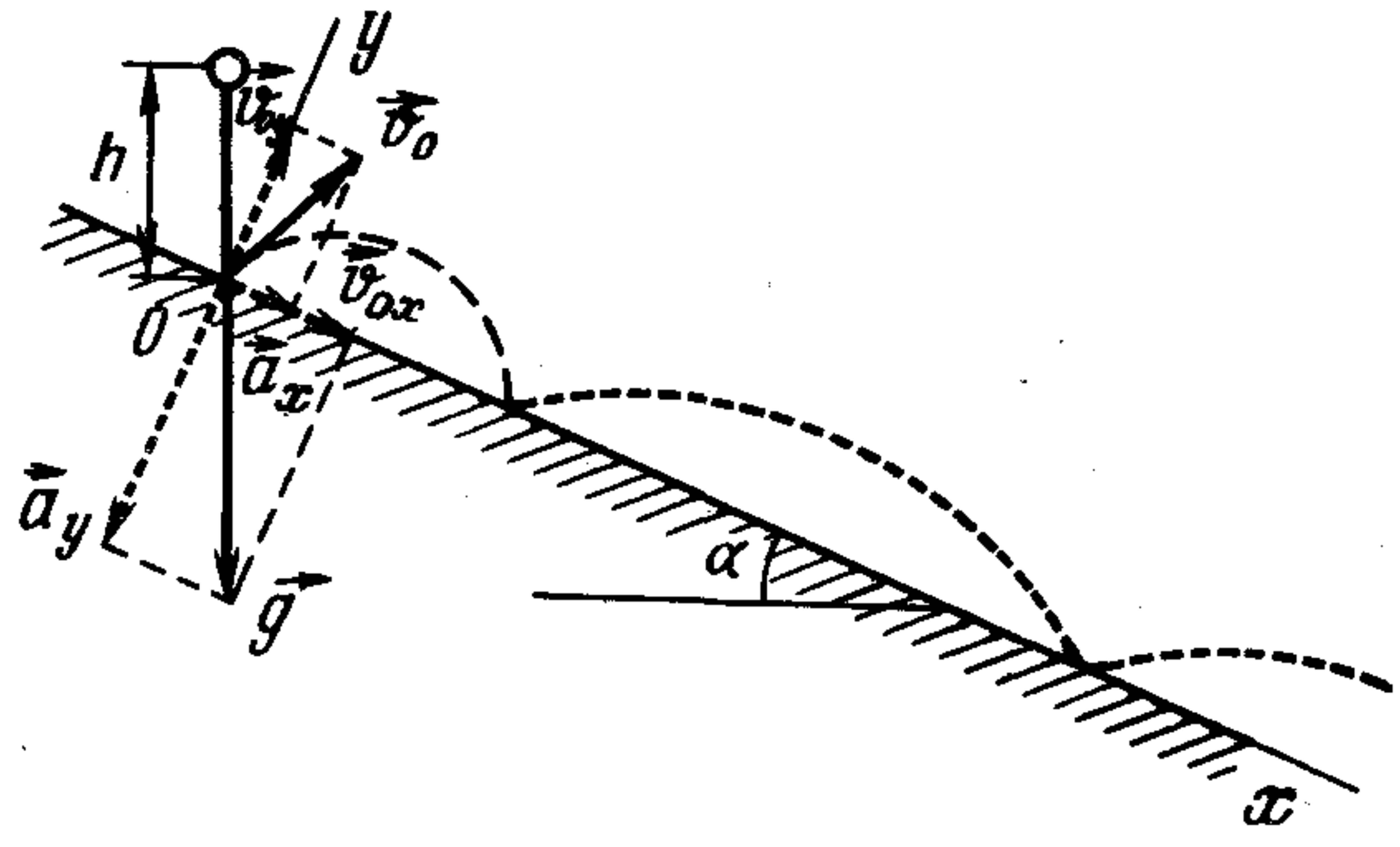
69. A ball falls freely from height $H$ onto a $45^\circ$ inclined plane and bounces elastically at the same speed. Find the distances between successive bounces. Solve for any angle $\alpha$.
Answer
$4H\sqrt{2}$; $s_1 = 8H \sin \alpha$; $s_1:s_2:s_3 = 1:2:3$.
Solution
See the previous problem. The distance from the place of the first impact to the second will be determined from the relation $x = v_{0x} t + a_x t^2 / 2$, where $v_{0x} = v_0 \sin \alpha$ and $a_x = g \sin \alpha$ (see figure). Substituting the value $t$ obtained in the previous problem, we find that $ \begin{aligned} s_1 &= v_0 \dfrac{2v_0}{g} \sin \alpha + \dfrac{g}{2} (\dfrac{2v_0}{g})^2 \sin \alpha \\ &= \dfrac{4v_0^2}{g} \sin \alpha \\ &= 8H \sin \alpha; \end{aligned} $ and for the components of the velocity of the body $v_{2x}$ and $v_{2y}$ at the moment of the second collision, respectively: $v_{2y} = v_{0y} - a_y t = v_0 \cos \alpha - g \dfrac{2v_0}{g} \cos \alpha = -v_{0y};$ $ \begin{aligned} v_{2x} &= v_{0x} + a_x t \\ &=v_0 \sin \alpha + g \dfrac{2v_0}{g} \sin \alpha \\ &= 3v_0 \sin \alpha, \end{aligned} $ and at the moment of the n-th collision: $v_{ny} = -v_{0y},$ $v_{nx} = (2n-1)v_0 \sin \alpha.$ The average velocities along the $x$-axis between impacts are respectively equal: $2v_0 \sin \alpha,\quad 4v_0 \sin \alpha,\quad 6v_0 \sin \alpha,$ i.e., they relate as 1:2:3, and since the time of motion between impacts is the same, then $s_1:s_2:s_3... = 1:2:3.$ 
70. A mountain's distance is determined by the time between a gunshot and its echo. What error $\tau$ is acceptable in timing if the distance is at least 1 km and must be determined within 3%? Sound speed $c = 330\, \text{m/s}$.
Answer
$\tau \le 0.09$ s.
Solution
The error in determining the time between the shot and the arrival of the echo is $2\tau$ seconds. This leads to an error in determining the distance traveled by sound, equal to $2\tau c$ meters. The path traveled by sound is equal to twice the distance to the mountain $2x$, therefore the relative error in determining this distance is $2\tau c / (2x) = \tau c / x$. This is also the relative error in determining the distance to the mountain. Since $\tau c / x \le 0.03$, then $\tau \le 0.03 (x/c)$. Considering that $x \ge 1000$ m, we find that the error in determining the moments of the shot and the arrival of the echo should not exceed 0.09 s.
71. A well's depth is measured by dropping a stone and timing the splash sound. For what minimum time $\tau$ must sound travel time be accounted for? Sound speed $c = 330\, \text{m/s}$.
Answer
$\tau \approx 1.77$ s.
Solution
If we do not take into account the time of sound propagation, we get that the depth of the well is $h_1 = g\tau^2/2$. Taking into account the time of sound propagation $\tau = t_1 + t_2$, where $t_1 = \sqrt{2h/g}$ is the time of the stone's fall, and $t_2 = h/c$ is the time of sound propagation ($h$ is the true depth of the well): $\tau = \dfrac{h}{c} + \sqrt{\dfrac{2h}{g}}.\tag{1}$ The error in measuring the depth of the well is $\dfrac{\Delta h}{h} =\dfrac{h_1 - h}{h} = 0.05.$ Hence $h = 0.95 h_1 = 0.95 \dfrac{g\tau^2}{2}.$ Substituting this expression into equation (1) and solving the resulting equation, we find $\tau = \dfrac{2(1 - 1/\sqrt{0.95})c}{0.95 g} \approx 1.77\text{ s}.$