1. Find the linear speed $v$ of the Earth during its orbital motion. The average radius of the Earth's orbit is $R = 1.5 \times 10^8$ km.
Answer
$v \approx 30$ km/s.
2. An airplane propeller with a radius of 1.5 m rotates during landing with a frequency of 2000 min$^{-1}$. The landing speed of the airplane relative to the Earth is 162 km/h. Determine the speed of a point on the tip of the propeller. What is the trajectory of motion of this point?
Answer
$v \approx 316$ m/s; the point describes a helical line with a pitch $h \approx 1.35$ m.
3. A disk of radius $R$ rolls without slipping with a constant speed $v$. Find the geometric locus of points on the disk that currently have a speed $v$.
Answer
The velocity $v$ at this moment is possessed by points lying on an arc of radius $R$, whose center is at the point of contact between the disk and the plane (instantaneous center of rotation).
4. A cylindrical roller of radius $R$ is placed between two parallel rails. The rails move in the same direction with speeds $v_1$ and $v_2$ (see figure). Determine the angular velocity of rotation of the roller and the speed of its center, assuming no slipping. Solve the problem for the case where the speeds of the rails are directed in opposite directions. 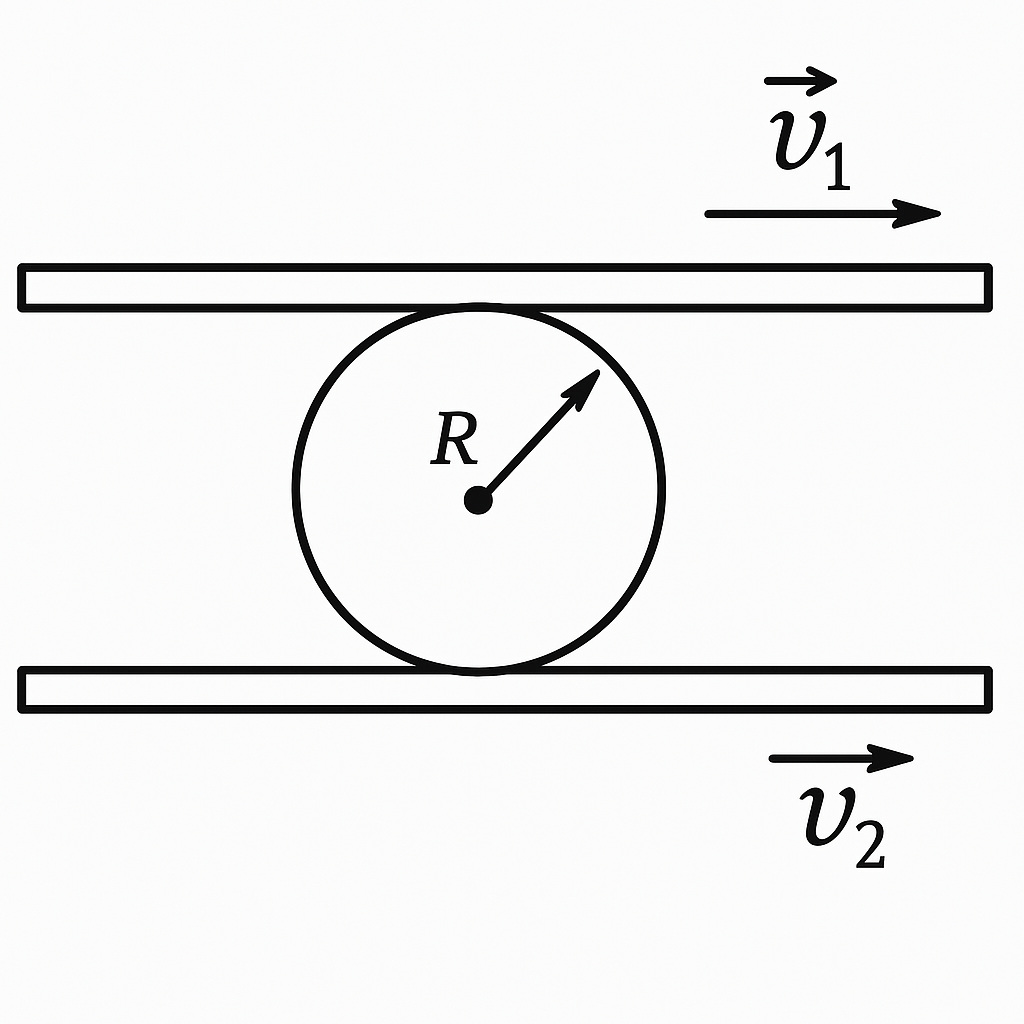
Solution
Let the roller move translationally with velocity $v$ and rotate about its axis with angular velocity $\omega$. The linear velocity of points on the roller in the coordinate system associated with its axis is $\omega R$. The points of contact between the roller and the racks also have this velocity. Since there is no slipping, this is also the velocity of the racks. In the coordinate system associated with the Earth, the velocities of the racks are equal to the sum of their velocities relative to the cylinder axis and the velocity of the cylinder axis relative to the Earth. Therefore, $v_1 = v + \omega R,\qquad v_2 = v - \omega R.$ From this, $v = \frac{1}{2}(v_1 + v_2),\qquad \omega = \frac{1}{2R}(v_1 - v_2).$ For the case where the rack velocities are directed in opposite directions ($v_1 = v + \omega R$, $v_2 = \omega R - v$), we get: $v = \frac{1}{2}(v_1 - v_2);\qquad \omega = \frac{v_1 + v_2}{2R}.$
5. A hoop of radius $R$ rolls without slipping along a horizontal plane with a constant speed $v_c$. What are the speeds and accelerations of various points on the hoop relative to the Earth? Express the speed as a function of the angle between the vertical and the line drawn between the point of contact of the hoop with the plane and the given point on the hoop.
Answer
$v_A = 2v_c \cos \alpha$. The accelerations of all points on the rim are centripetal and equal to $a_{cp} = v_c^2/R$.
Solution
The angular velocities of rotation of all points on the rim relative to the axis passing through the point of contact of the hoop with the plane (instantaneous center of rotation) are identical and equal to $\omega = v_c/R$. The linear velocity of point $A$ is $v_A = \omega r = \omega (2R \cos \alpha) = \frac{v_c}{R} 2R \cos \alpha = 2v_c \cos \alpha$ and is perpendicular to OA (see figure). Since the translational motion of the hoop is uniform, its points only have centripetal acceleration. This becomes obvious when considering the motion of the hoop in an inertial frame of reference moving with velocity $v_c$. 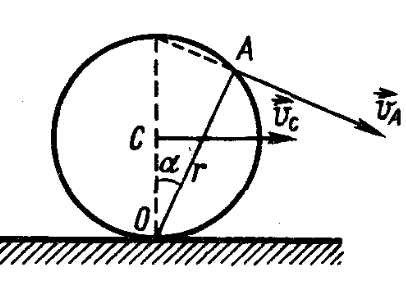
6. A car moves with a speed $v = 60$ km/h. With what frequency $n$ do its wheels rotate if they roll on the highway without slipping, and the outer diameter of the tires is $d = 60$ cm? Find the centripetal acceleration $a_{cp}$ of the outer layer of rubber on its tires.
Answer
$n \approx 8.84 \text{ s}^{-1}$;
$a_{cp} \approx 926 \text{ m/s}^2$ (this acceleration is 94.4 times greater than $g$).
7. A thin-walled cylinder, rotating with speed $\omega_0$ about its axis, is placed on a horizontal plane. What will be the speed of the cylinder's axis when the slipping of the cylinder relative to the plane stops?
Answer
$v = v_0/2$.
Solution
1st method. When slipping, a constant friction force acts on the cylinder from the plane, which accelerates its translational motion and decelerates its rotational motion. After time $t$, the translational velocity will be $v = at$, and the linear velocity of rotational motion relative to the cylinder axis will be $v_r = v_0 - at$ (since the cylinder is thin-walled, all elementary masses have the same acceleration $a$ relative to the cylinder axis, equal in magnitude to the acceleration of the translational motion).
The velocity of the point on the cylinder touching the plane is equal to the difference in velocities $v_r - v$. Slipping will stop when this velocity becomes zero:
$v_r - v = (v_0 - at) - at = 0,$
whence $at = v_0/2$. Thus, the translational velocity (velocity of the cylinder axis) at this moment will be $v_0/2$ and will not change further.
2nd method. While slipping, the cylinder performs work against the friction force $F$ applied to it: $A = F S_{sl},$
where $S_{sl}$ is the path traveled by the point (more precisely, the line) of application of the friction force on the cylinder surface during its sliding on the plane over time $t$: from the moment of contact, when the sliding velocity $v_{sl} = v_0$, until the moment slipping stops ($v_{\text{sl}} = 0$). Since the motion is uniformly accelerated, the average sliding velocity is $v_0/2$. Thus,
$A = F S_{\text{sl}} = F v_0 \frac{t}{2}.$
According to the work-energy theorem, the work $A$ equals the decrease in the kinetic energy of the cylinder:
$\frac{mv_0^2}{2} - (\frac{mv^2}{2} (\text{trans}) + \frac{mv^2}{2} (\text{rot})) = F \frac{v_0 t}{2}$
(cylinder is thin-walled, therefore $T_{trans} = T_{rot}$, see problem 50). The friction force $F$, which brakes the cylinder's rotation to velocity $v$ over time $t$, simultaneously imparts translational motion with the same velocity $v$. Writing Newton's second law for the translational motion in impulse form $Ft = mv$ and substituting $Ft$ with $mv$ in equation (1), we obtain an equation from which we find $v = v_0/2$.
8. Does the resultant of all forces applied to a body moving uniformly in a circle perform work?
Answer
No. This force, according to the problem statement, ensures the uniform rotation of the body, is a constant magnitude centripetal force, which at each moment in time is directed perpendicular to the displacement of the body and does no work.
9. A load of mass $m$ can slide without friction along a horizontal rod, which rotates around a vertical axis passing through one of its ends. The load is connected to this end of the rod by a spring with spring constant $k$. At what angular velocity $\omega$ will the spring stretch by 50% of its original length?
Answer
$\omega = \sqrt{\frac{1}{3} \frac{k}{m}}$.
Solution
The centripetal acceleration $a_{\text{cp}} = \omega^2 (l_0 + \Delta l) = 1.5 l_0 \omega^2$ ($l_0$ is the initial length of the spring; $\Delta l$ is its extension) is imparted to the mass by the tension force of the spring, which, according to Hooke's law, is $F = k \Delta l = 0.5 l_0 k.$ Therefore, $1.5 m \omega^2 l_0 = 0.5 l_0 k.$ Hence $\omega = \sqrt{\frac{1}{3} \frac{k}{m}}.$
10. Two point masses $m_1$ and $m_2$ are attached to strings and are located on a perfectly smooth table. The distances from them to the fixed end of the string are $l_1$ and $l_2$ respectively (see figure). The system rotates in a horizontal plane around the axis passing through the fixed end, with an angular velocity $\omega$. Find the tension forces in the sections of the string $T_1$ and $T_2$. 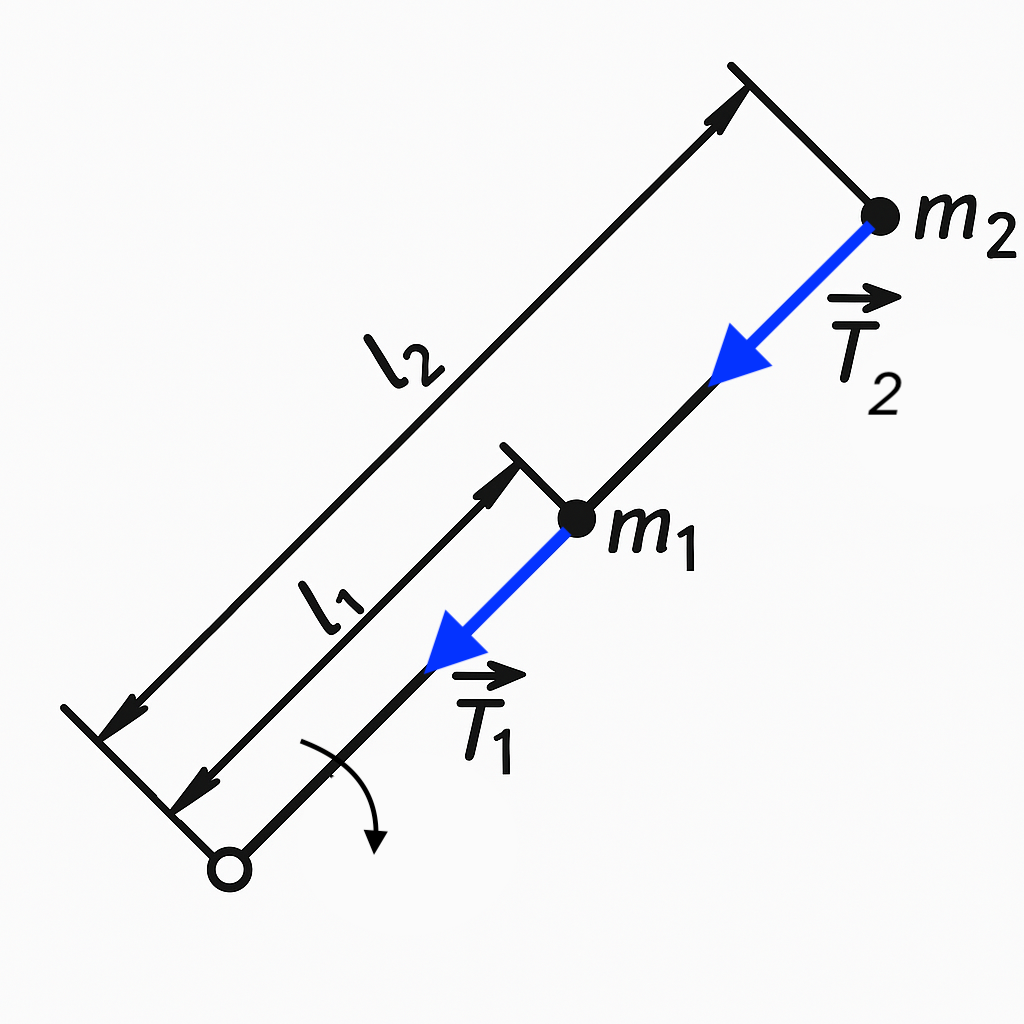
Answer
$T_1 = (m_1 l_1 + m_2 l_2) \omega^2$;
$T_2 = m_2 \omega^2 l_2$.
Hint
The force $T_2$ imparts centripetal acceleration to the outermost mass; the force $(T_1 - T_2)$ imparts it to the other mass (see the following figure). 
11. A person sits on the edge of a circular horizontal platform of radius $R = 4$ m. With what frequency $n$ must the platform rotate around a vertical axis so that the person cannot stay on it with a coefficient of friction $k = 0.27$?
Answer
$n = 6.75 \text{ min}^{-1}$.
Solution
A person cannot stay on the platform if the maximum possible static friction force with the platform is insufficient to provide the necessary centripetal acceleration, i.e., $F_{fr} = kmg < m\omega^2 R$ or $n = \omega/(2\pi) > \frac{1}{2\pi} \sqrt{kg/R}.$
12. A body of mass $m$ is on a horizontal disk at a distance $r$ from the axis. The disk begins to rotate with a small acceleration. Construct a graph of the dependence of the radial component of the friction force acting on the body on the angular velocity of the disk's rotation. At what value of the angular velocity will the body begin to slide?
Answer
See the following figure. 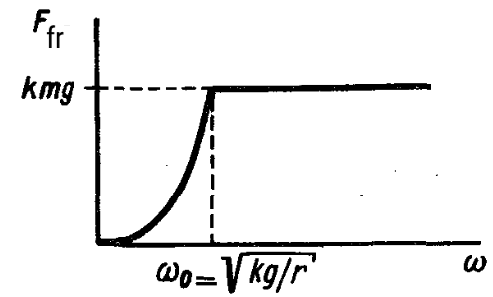
Hint
Before the body starts sliding, the friction force provides it with centripetal acceleration $a = \omega^2 r.$ Therefore, considering the smallness of the tangential acceleration according to the condition, $F_{fr} \approx m\omega^2 r \le kmg.$ The body starts sliding at $\omega = \omega_0$, such that $F_{\text{cp}} = kmg$, i.e., when $\omega_0^2 r = kg$.
13. A stone of mass $m = 0.5$ kg, tied to a rope of length $l = 50$ cm, rotates in a vertical plane. The tension force in the rope when the stone passes the lowest point of the circle is $T = 44$ N. To what height $h$ above the lowest point of the circle will the stone rise if the rope is cut at the moment when its velocity is directed vertically upwards?
Answer
$h = l(T - mg)/(2mg) \approx 2.0$ m.
Hint
The kinetic energy of the stone at the lowest point of the circle completely converts into its potential energy during the ascent: $mv^2/2 = mgh$, where $h$ is the height of ascent above the lowest point of the circle. Further, write the equation of dynamics of rotational motion for the moment of passing the lowest point $mv^2/l = T - mg$ and solve both equations together to find the answer.
14. An athlete throws a hammer (a weight on a cable) a distance $l = 70$ m along a trajectory providing maximum range. What force $T$ acts on the athlete's hands at the moment of release? The mass of the hammer is $m = 5$ kg. Assume the athlete spins the hammer in a vertical circle of radius $R = 1.5$ m. Neglect air resistance.
Answer
$T = mg[\frac{l}{R} - (1 + \frac{\sqrt{2}}{2})] \approx 2205$ N.
Hint
The flight distance $l$ will be maximum if the hammer's velocity is directed at an angle $\alpha = 45^\circ$ to the horizontal. In this case (see problem 63 in Chapter: Kinematics) $l_0 = \sqrt{v_0^2/g}$, where $l_0$ is the flight distance when the points of takeoff and landing are at the same height above the Earth's surface. In our case (see figure) $l_0 = l - R$. 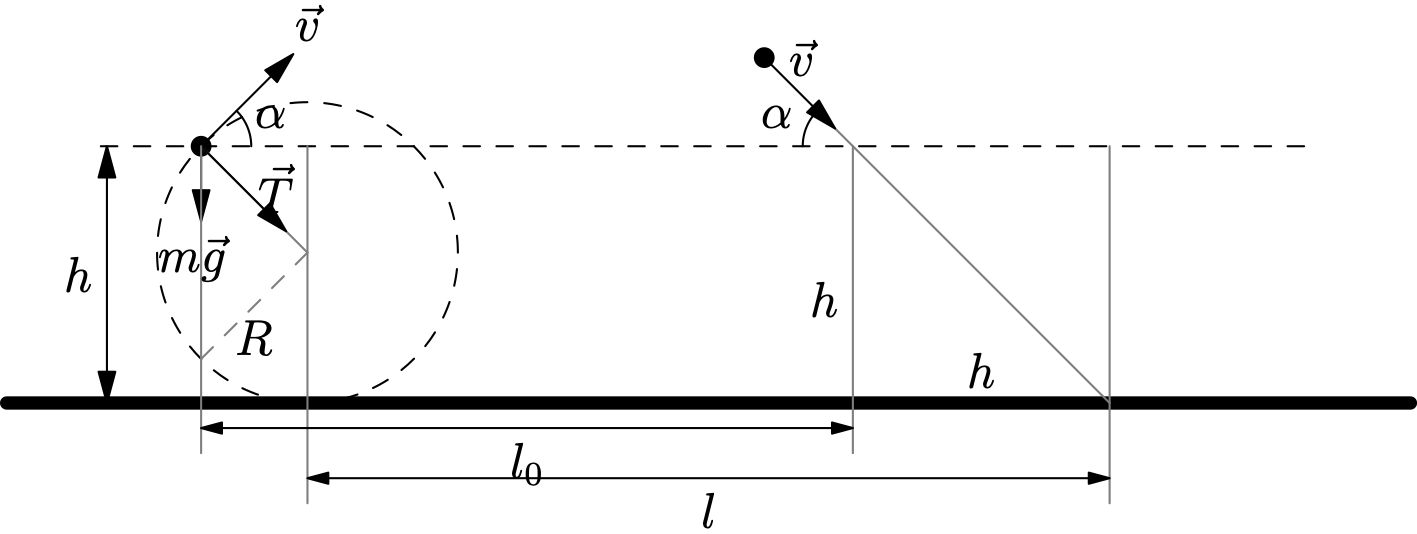
15. A car of mass $M = 3 \times 10^3$ kg moves with a constant speed $v = 36$ km/h: a) over a horizontal bridge; b) over a convex bridge; c) over a concave bridge. The radius of curvature of the bridge in the last two cases is $R = 60$ m. With what force does the car press on the bridge (in the last two cases) at the moment when the line connecting the center of curvature of the bridge with the car makes an angle $\alpha = 10^\circ$ with the vertical?
Answer
a) $F_1 = mg \approx 29400$ N;
b) $F_2 = mg (\cos \alpha - \frac{v^2}{gR}) \approx 24000$ N;
c) $F_3 = mg (\cos \alpha + \frac{v^2}{gR}) \approx 34000$ N.
At the moment the car passes the middle of the bridge, $F_2 = 24400$ N; $F_3 = 34400$ N.
Hint
Two forces act on the car: the force of gravity $F_t = mg$ and the normal reaction force of the bridge $N$, which, according to Newton's third law, is equal in magnitude to the force $F$ of the car's pressure on the bridge. Along the curved bridge, the car moves with centripetal acceleration, imparted to it by the resultant of the force $N$ and the radial component of the gravity force, equal to $mg \cos \alpha$ (see figure). In accordance with Newton's second law, one can write $mv^2/R = mg \cos \alpha - N_2$ for a convex bridge and $mv^2/R = N_3 - mg \cos \alpha$ for a concave bridge. 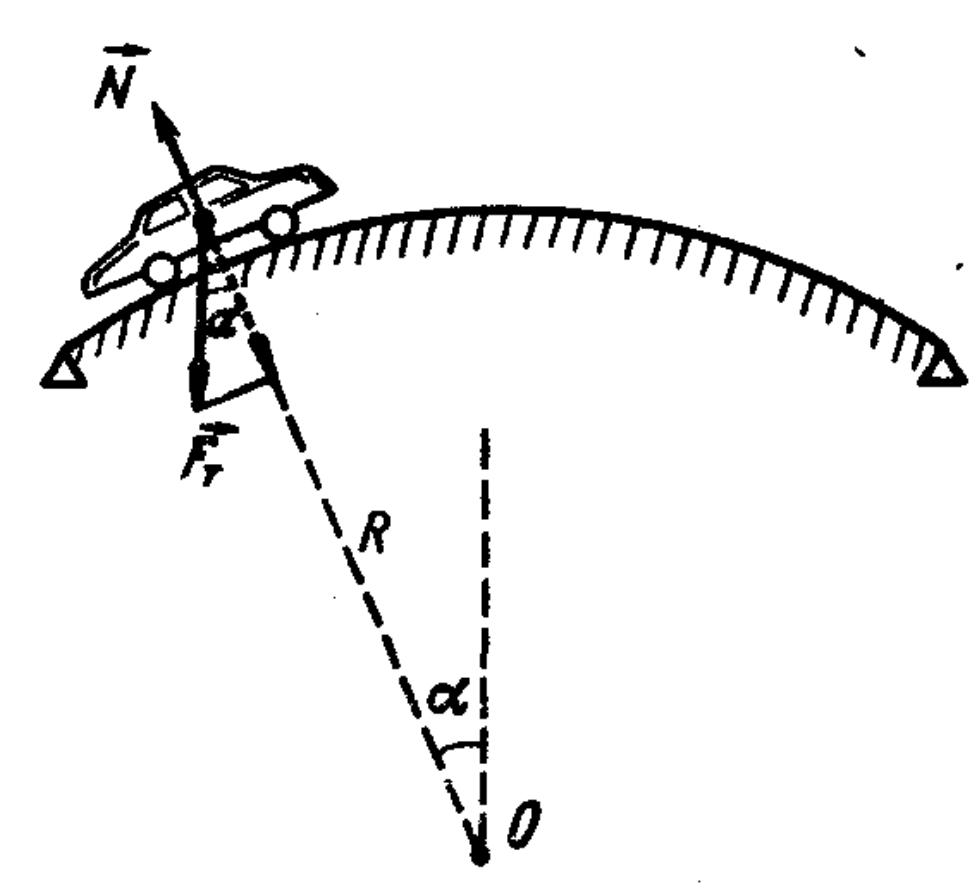
16. A car of mass $m = 2$ t moves over a convex bridge with radius of curvature $R = 90$ m at a speed $v = 54$ km/h. At a point on the bridge, the direction to which from the center of curvature makes an angle $\alpha$ with the direction to the top of the bridge, the car exerts a force $F = 14400$ N. Determine the angle $\alpha$.
Answer
$\alpha = \arccos (\frac{F}{mg} + \frac{v^2}{gR}) \approx 8.2^\circ$.
17. A ball of mass $m = 100$ g is suspended on a string of length $l = 1$ m. The ball was spun so that it began to move in a circle in a horizontal plane. In doing so, the angle formed by the string with the vertical is $\alpha = 60^\circ$. Determine the total work done in spinning the ball.
Answer
$A = mgl (1 + \frac{1}{2} \tan \alpha \sin \alpha - \cos \alpha) \approx 1.23$ J.
Hint
The work goes into increasing the potential and kinetic energy. The speed of the ball is found from the condition $mv^2/(l \sin \alpha) = mg \tan \alpha$, and $h = l (1 - \cos \alpha)$.
18. What is the maximum speed at which a car can move on a turn with a radius of curvature $R = 150$ m, so that it does not skid, if the coefficient of sliding friction of the tires on the road is $k = 0.42$?
Answer
$v = \sqrt{kgR} \approx 89$ km/h.
Hint
See problem 11.
19. 1. What must be the maximum coefficient of sliding friction $k$ between the tires of a car and asphalt for the car to be able to negotiate a curve of radius $R = 200$ m at a speed $v = 100$ km/h?
- A car with all driving wheels, starting from rest, uniformly gains speed while moving along a horizontal section of road representing an arc of a circle $\alpha = 30^\circ$ with radius $R = 100$ m. What is the maximum speed at which the car can exit onto the straight section of the path? The coefficient of friction between the wheels and the ground is $k = 0.3$.
Answer
1. $k = v^2/(gR) \approx 0.4$.
- $v = \dfrac{\sqrt{2kgR\alpha}}{\sqrt{1 + 4\alpha^2}} \approx 14.5$ m/s.
Hint and Solution
- See problem 11.
The acceleration $a$ of the car is composed of the constant tangential acceleration $a_t$, which provides the car's acceleration, and the centripetal acceleration $a_{cp} = v^2/R$ ($v$ is the car's speed). Therefore
$a = \sqrt{a_t^2 + \frac{v^4}{R^2}}.$
The external force providing acceleration to the car is the friction force of the wheels on the road. Since the friction force cannot exceed $kmg$ ($m$ is the mass of the car), the maximum acceleration $a$ at the moment the car transitions to the horizontal section of the road cannot be greater than $kg$:
$\sqrt{a_t^2 + \frac{v^4}{R^2}} = kg.$
Since
$v = \sqrt{2a_t l}$
($l = R\alpha$ is the path traveled by the car; $\alpha = \pi/6$), then
$a_t = \frac{v^2}{2l} = \frac{v^2}{2R\alpha},$
and after substitution we get
$\frac{v^2}{R} \sqrt{\frac{1}{4\alpha^2} + 1} = kg.$
Hence $v = \frac{\sqrt{2kgR\alpha}}{\sqrt{1 + 4\alpha^2}}$.
20. A train moves along a curve of radius $R = 800$ m with a speed $v = 72$ km/h. Determine how much higher the outer rail must be than the inner rail so that no lateral force arises on the wheels. The distance between the rails horizontally is taken as $d = 1.5$ m.
Answer
$\Delta h \approx 7.65$ cm.
Hint
The resultant force $\vec{F}$ of the wagon's weight $m\vec{g}$ and the reaction force of the rails $\vec{N}$ imparts centripetal acceleration $a_{cp}$ to the wagon; $m a_{\text{cp}} = m\vec{g} + \vec{N};$ the resultant is directed horizontally (since its direction must coincide with the direction of the train's acceleration) and is equal to $mg \tan \alpha$ (see figure): $mv^2/R = mg \tan \alpha.$ Hence $\tan \alpha = \frac{v^2}{gR}.$ The upper rail exceeds the lower one by the amount $\Delta h = d \tan \alpha = d v^2/(gR).$
- In this section, the dimensions of the bodies are considered much smaller than the radius of rotation, i.e., the entire mass of the body is considered concentrated at one point - its center of mass.
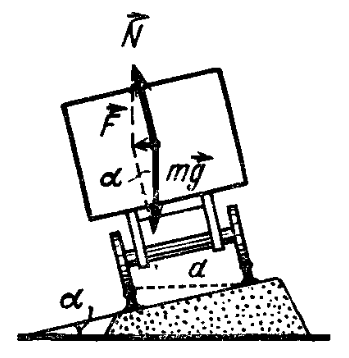
21. A motorcyclist rides on a horizontal road at a speed of 72 km/h, making a turn with a radius of curvature of 100 m. By how much must he lean in this case so as not to fall on the turn?
Answer
$\alpha \approx 22^\circ$.
Solution
For a motorcyclist to move in a circle, he must lean so that the resultant of the three forces applied to him: gravity $m\vec{g}$, normal reaction force of the road $\vec{N}$, and friction force with the road $\vec{F}_{fr}$ (see figure) - provides him with centripetal acceleration. Since the center of mass of the motorcyclist does not move vertically, $N = mg$. The centripetal acceleration is ultimately provided by the friction force: $mv^2/R = F_{fr}$.
The resultant $\vec{R} = \vec{N} + \vec{F}{fr}$, obviously, must pass through the center of mass of the motorcyclist (the moment of the resultant relative to the center of mass must be zero). Therefore
$\cot \alpha = N/F{fr} = mg / (mv^2/R) = gR/v^2.$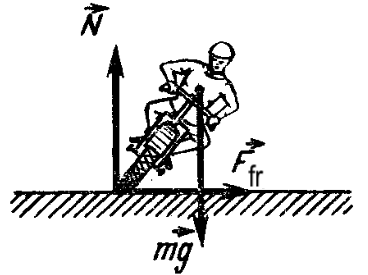
22. 1. What is the maximum speed $v$ at which a motorcyclist can ride on a horizontal plane, describing an arc of radius $R = 90$ m, if the coefficient of sliding friction $k = 0.4$?
- At what angle $\phi$ from the vertical direction must he lean in this case?
- What will be the maximum speed of the motorcyclist if he rides on a banked track with an angle of inclination $\alpha = 30^\circ$ at the same radius of curvature and coefficient of friction?
- What must be the angle of inclination $\alpha_0$ of the track so that the speed of the motorcyclist can be arbitrarily large?
Answer
1. $v \approx 18.8$ m/s.
- $\phi \approx 21.8^\circ$.
- $v_{\text{max}} \approx 33.5$ m/s.
- $\alpha_0 = \arctan (1/k)$.
Solution
- Centripetal acceleration is provided by the friction force (see previous problem), therefore $mv^2/R = F_{fr}$. But the friction force cannot exceed the value
$F_{\text{fr.max}} = kN = kmg,$
meaning the motorcyclist's speed cannot be greater than some limiting value, determined by this maximum possible value of the friction force:
$mv_{\text{max}}^2/R = kmg.$
Hence $v_{\text{max}} = \sqrt{kgR}.$ - The angle of inclination of the motorcyclist at this speed must be equal to:
$\phi = \arctan \frac{v_{\text{max}}^2}{gR} = \arctan k.$ - In creating the centripetal acceleration, the horizontal components of the friction force and the track reaction force will participate (see figure):
$mv_{\text{max}}^2/R = F_{fr.max} \cos \alpha + N \sin \alpha. \tag{1}$
The sum of the vertical components of the forces acting on the motorcycle must be zero (there is no acceleration in the vertical direction):
$F_{fr.max} \sin \alpha + mg - N \cos \alpha = 0.\tag{2}$
Maximum friction force
$F_{fr.max} = kN.\tag{3}$
Solving equations (1), (2), and (3) together, we get
$v_{\text{max}} = \sqrt{gR \frac{k + \tan \alpha}{1 - k \tan \alpha}}.$ Hint. From part 3, it follows that
$v_{\text{max}} \to \infty$ when $1 - k \tan \alpha \to 0$, whence
$\alpha_0 = \arctan (1/k).$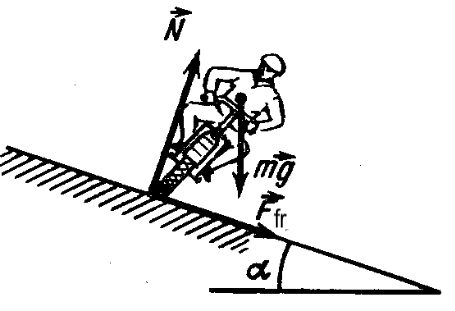
23. An airplane performs a turn, moving along an arc of a circle with a constant speed $v = 360$ km/h. Determine the radius $R$ of this circle if the body of the airplane is turned around the direction of flight by an angle $\alpha = 10^\circ$.
Answer
$R \approx 5780$ m.
Solution
The aircraft changes its direction of flight by transitioning to motion along an arc of a circle by banking its fuselage around the direction of flight. In this case, the centripetal acceleration is imparted to the aircraft by the resultant of the gravity force and the lift force, perpendicular to the plane of the wings. This resultant is equal to $mg \tan \alpha$ (see figure). According to Newton's second law $mg \tan \alpha = mv^2/R,$ whence $R = v^2/(g \tan \alpha).$ 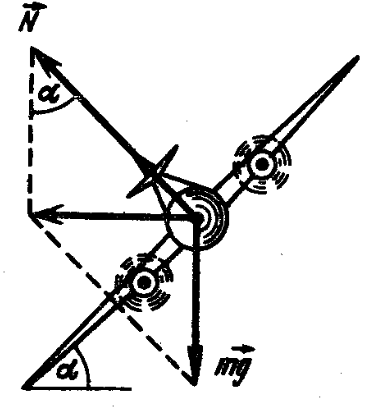
24. A car moves uniformly on a road turn of radius $R = 100$ m. The center of gravity of the car is at a height $h = 1$ m, the width of the car's track is $a = 1.5$ m. Determine the speed $v$ at which the car might tip over. The car does not slide in the transverse direction.
Answer
$v \approx 26.1$ m/s.
Solution
When the car turns, the pressure on its wheels, and hence the forces acting on the car wheels from the road, are redistributed. At the maximum permissible speed of the car, the forces acting on it from the road will be applied to the outer wheels and are equal to: a) the reaction force $N = mg$ (numerically equal to the gravity force acting on the car, as there is no acceleration in the vertical direction) and b) the friction force $F_{fr} = mv^2/R$ (as it provides the car with centripetal acceleration). The car will overturn if the direction of the resultant of these forces passes below the center of mass of the car - in this case, there is an overturning moment of force relative to the center of mass. At the critical speed, this resultant passes through the center of mass of the car and therefore (see figure) $N/F_{fr} = \tan \alpha = (a/2)/h = a/(2h),$ or $mg / (mv^2/R) = a/(2h),$ whence $v = \sqrt{gRa/(2h)}.$ 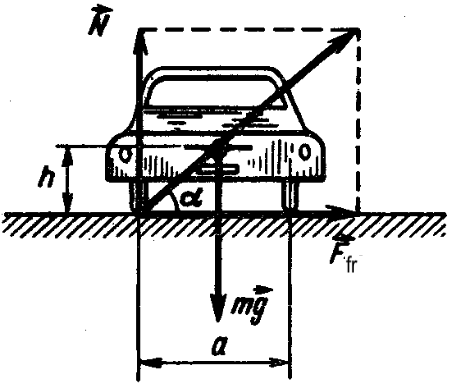
25. A driver, driving a car, suddenly noticed a fence ahead, perpendicular to the direction of his movement. What is more advantageous to do to prevent an accident: brake or turn aside?
Answer
Brake.
Solution
During braking, the friction force $F_{fr}$ must perform work $A = F_{fr} x$ ($x$ is the braking distance), equal to the kinetic energy the car had before braking: $F_{fr} x = mv^2/2$. Hence the braking distance $x = mv^2/(2 F_{fr})$. If the driver, without braking, turns aside, the car will move along an arc of a circle, and the centripetal acceleration $a_{cp} = v^2/R$ ($R$ is the radius of curvature) will be provided to the car by the same friction force. From the equation of motion $F_{fr} = mv^2/R$, we find that the turning radius will be $R = mv^2/F_{fr}$, i.e., it is twice the 'braking distance'. This means it is more advantageous to brake than to turn.
26. In a train car, moving uniformly along a curved path with a speed $v = 72$ km/h, a load is weighed on a spring scale. The mass of the load is $m = 5$ kg, and the radius of curvature of the path is $R = 200$ m. Determine the reading of the spring scale (the tension force of the spring $T$).
Answer
$T \approx 51$ N.
Solution
Centripetal acceleration is imparted to the suspended mass by the resultant of the gravity force and the tension force $T$ of the spring. This resultant is equal to $mg \tan \alpha$ (see figure). According to Newton's second law $mg \tan \alpha = mv^2/R$, hence $\tan \alpha = v^2/(gR)$. The tension force of the spring $T = mg/\cos \alpha = mg \sqrt{1 + \tan^2 \alpha} = mg \sqrt{1 + \frac{v^4}{g^2 R^2}}.$ 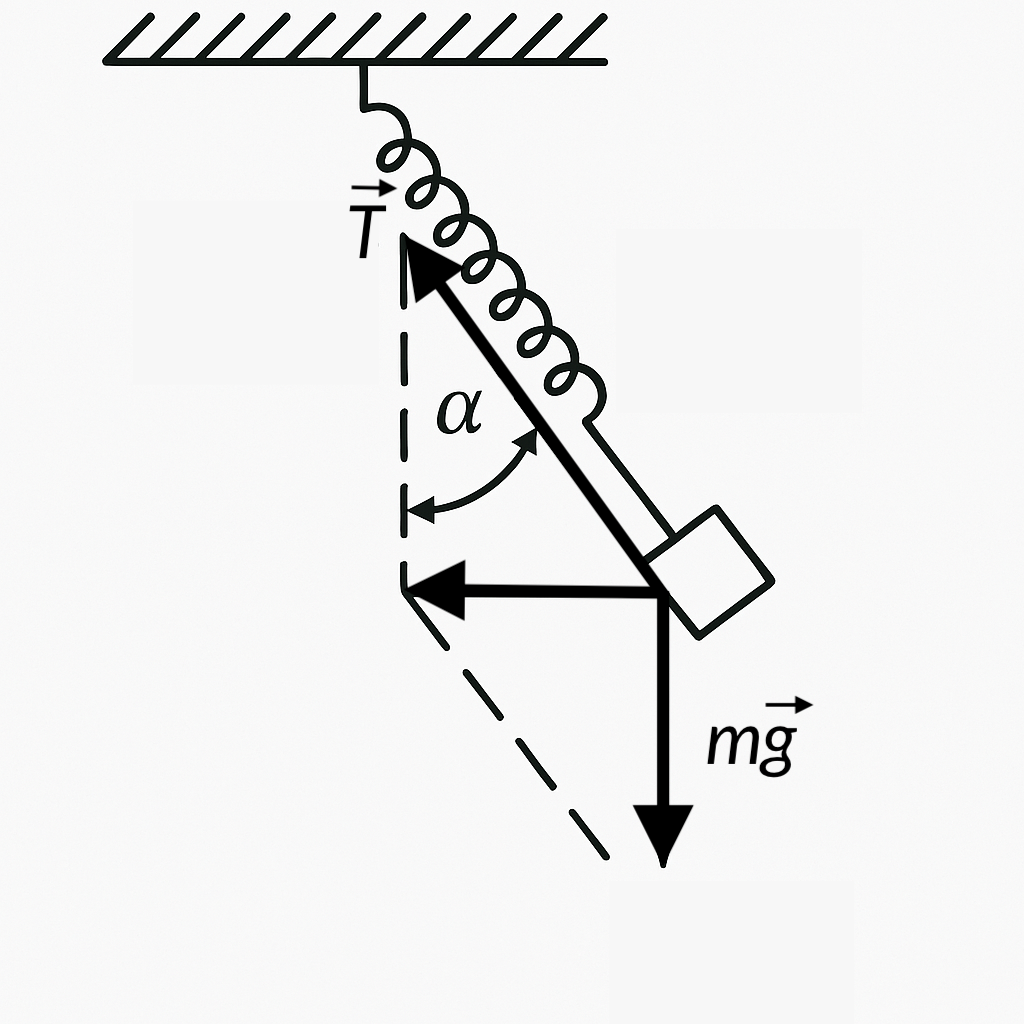
27. Find the separating force $F_{sep}$ acting on cream (density $\rho_c = 0.93$ g/cm$^3$) from skim milk ($\rho_m = 1.03$ g/cm³) per unit volume, if the separation occurs:
a) in a stationary container;
b) in a centrifugal separator rotating with a frequency of 6000 min$^{-1}$, if the liquid is at a distance $r = 10$ cm from the axis of rotation.
Answer
a) $F_{sep} = (\rho_m - \rho_c) g \approx 980 \text{ N/m}^3$;
b) $F_{sep} = (\rho_m - \rho_c) \omega^2 r \approx 3.94 \times 10^6 \text{ N/m}^3$.
Hint
a) In a stationary vessel, the separating force is the Archimedean (buoyant) force.
b) If the volume $V$, occupied by a particle of cream, were occupied by milk, it would be in equilibrium. This means that a force $F_1 = \rho_m \omega^2 r V,$ directed towards the axis of rotation, acts on the cream particle from the surrounding milk. This force turns out to be greater than the force required for the circular motion of the cream particle, which is $F_2 = \rho_c \omega^2 r V.$
The difference between these forces is the separating force.
28. An airplane performs a 'loop-the-loop' with a radius $R = 100$ m and moves along it with a speed $v = 280$ km/h. With what force $F$ will the pilot's body of mass $M = 80$ kg press on the seat of the airplane at the top and bottom points of the loop?
Answer
$F_{\text{top}} = \frac{Mv^2}{R} - Mg \approx 4030$ N, $F_{\text{bottom}} = \frac{Mv^2}{R} + Mg \approx 5630$ N.
Hint
See problem 15. The centripetal acceleration at the top and bottom points of the 'dead loop' is imparted to the pilot by the resultant of the gravity force and the reaction force of the seat.
29. Determine the tension force $T$ of the giant swing cable, if the mass of the person is $M = 70$ kg and the cable forms an angle $\alpha = 45^\circ$ with the pole during rotation. With what angular velocity $\omega$ will the giant swings rotate if the length of the suspension is $l = 5$ m?
Answer
$T = Mg/\cos \alpha \approx 990$ N; $\omega = \sqrt{g/(l\cos\alpha)} \approx 1.68$ rad/s.
Hint
Centripetal acceleration is imparted to the person by the resultant of the gravity force and the tension force of the rope; this resultant is horizontal.
30. Find the period $T$ of rotation of a conical pendulum performing circular motions in a horizontal plane. The length of the string is $l$. The angle formed by the string with the vertical is $\alpha$.
Answer
$T = 2\pi \sqrt{l\cos\alpha/g}$. For small angles $T \approx 2\pi \sqrt{l/g}$.
Solution
Centripetal acceleration is imparted to the pendulum by the resultant of the gravity force $m\vec{g}$ and the tension force of the string $\vec{T}$ (see figure). This resultant lies in the plane of motion of the pendulum and is equal to $mg \tan \alpha$. According to Newton's second law, $m\omega^2 R = mg \tan \alpha$ or $\frac{4\pi^2}{T^2} l \sin \alpha = g \tan \alpha$ (since $R = l \sin \alpha$ and $\omega = 2\pi/T$). Hence $T = 2\pi \sqrt{l \cos \alpha / g}.$ 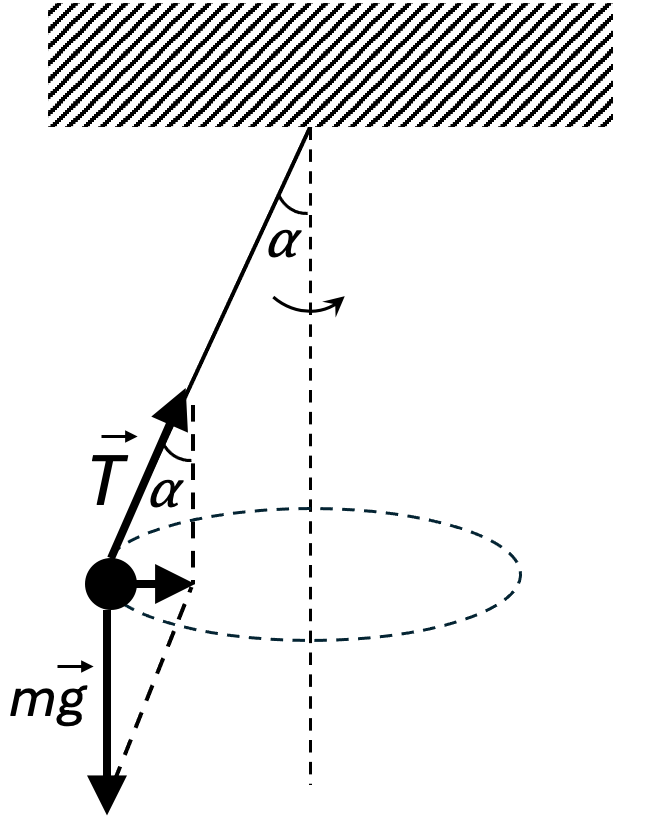
31. A small weight, suspended on a string, rotates in a horizontal plane such that the distance from the suspension point to the plane in which the rotation occurs is $h$. Find the frequency $n$ of rotation of the weight, considering it constant.
Answer
$n = \frac{1}{2\pi} \sqrt{g/h}$. (The answer does not depend on the length of the suspension.)
32. A chandelier of mass $m = 100$ kg is suspended from the ceiling on a metal chain of length $l = 5$ m. Determine the height $h$ to which the chandelier can be deflected so that the chain does not break during subsequent swings. It is known that the chain breaks when the tension force $T > 1960$ N.
Answer
$h \le (T - mg) l / (2mg) \approx 2.5$ m.
Solution
Two forces act on the chandelier at any point of the trajectory (see figure): the force of gravity $mg$ and the tension force of the chain $T$. When the chandelier passes the equilibrium position (point A), the forces are directed along the same line. Let's write the equation of Newton's second law for the chandelier at the moment it passes point A: $ma_{cp} = T - mg,$ where $a_{cp} = v^2/l$ is the centripetal acceleration. Then $mv^2/l = T - mg.\tag{1}$ From the law of conservation of energy, we find the speed of the chandelier at point A: $mgh = mv^2/2,$ or $v^2 = 2gh.\tag{2}$ Substituting expression (2) into equation (1), we have $m(2gh)/l = T - mg,$ whence $h = (T - mg) l / (2mg).$ According to the condition, $T < 2mg$, therefore, $h < 2.5 \text{ m}$. 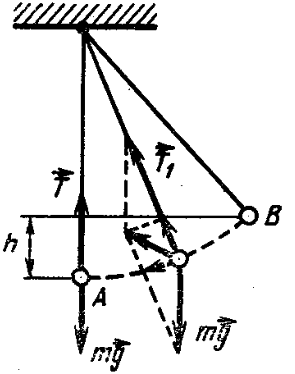
33. A ball of mass $m$ is suspended on an inextensible string. To what minimum angle $\alpha_{\text{min}}$ must the ball be deflected so that the string breaks during subsequent motion, if the maximum possible tension force of the string is $1.5 mg$?
Answer
$\alpha_{\text{min}} = \arccos 0.75 \approx 41.4^\circ$.
Hint
See the previous problem.
34. A pendulum is deflected to a horizontal position and released. At what angle $\alpha$ with the vertical will the tension force of the string be equal in magnitude to the force of gravity acting on the pendulum bob? Consider the pendulum as simple.
Answer
$\alpha = \arccos (1/3)$.
35. A load of mass $m$, tied to an inextensible string, rotates in a vertical plane. Find the maximum difference in the tension forces of the string.
Answer
$6mg$.
Hint
See the hint for problem 28. The relationship between the speeds of the mass at the top $v_t$ and bottom $v_b$ points is determined by the law of conservation of energy: $\frac{mv_b^2}{2} - \frac{mv_t^2}{2} = mg \cdot 2R.$
36. A gymnast 'swings the giant' on the high bar. The mass of the gymnast is $m$. Assuming that his entire mass is concentrated at the center of gravity, and the speed at the highest point is zero, determine the force acting on the gymnast's hands at the lowest point.
Answer
$5mg$.
Hint
See the previous problem and problem 28.
37. One weight is suspended on an inextensible string of length $l$, and another on a rigid weightless rod of the same length. What minimum speeds must be imparted to these weights so that they rotate in a vertical plane?
Answer
$v_{\text{min}} = \sqrt{5gl}$ for the string; $v_{\text{min}} = 2\sqrt{gl}$ for the rod.
Hint
In the case of a massless rod, the minimum speed $v_{\text{min}}$ of the mass at the lowest point is determined by the condition: the change in its potential energy upon rising from the lowest to the highest point equals the initial kinetic energy of the mass: $mg \cdot 2l = mv^2/2.$ The speed of the mass at the highest point is zero. In the case where the mass rotates on an inextensible string, this condition is insufficient; another condition is needed: the string must remain taut up to the highest point. The speed of the mass at the highest point cannot be zero, but must be such that the centripetal acceleration is provided to the mass only by the force of gravity: $mv_{top}^2/l = mg$. At this moment $T = 0$, which is the condition for the minimum speed.
38. A ball of mass $M$ is suspended on a string. In the taut state, the string was positioned horizontally and the ball was released. Derive the dependence of the string tension force $T$ on the angle $\alpha$ that the string currently makes with the horizontal direction. Check the derived formula by solving the problem for the case of the ball passing through the equilibrium position, when $\alpha = 90^\circ$.
Answer
$T = 3Mg \sin \alpha$; $T = 3Mg$.
Hint
See problem 32.
39. A simple pendulum of length $l$ and mass $M$ was deflected by an angle $\phi_0$ from the equilibrium position and given an initial velocity $v_0$, directed perpendicular to the string upwards. Find the tension force of the pendulum string $T$ as a function of the angle $\phi$ of the string with the vertical.
Answer
$\displaystyle T = Mg(3 \cos \phi - 2 \cos \phi_0 + \frac{v_0^2}{gl})$ until it comes to rest.
Hint
See problem 32. Consider the initial kinetic energy of the pendulum.
40. A weight, suspended on a string, is pulled aside so that the string assumes a horizontal position, and released. What angle $\alpha$ with the vertical does the string form at the moment when the vertical component of the weight's velocity is maximum?
Answer
$\cos \alpha = \sqrt{3}/3$; $\alpha \approx 54.7^\circ$.
Solution
The vertical component of the bob's velocity will increase until the vertical component of the resultant of the applied forces, gravity $m\vec{g}$ and string tension $\vec{T}$ (see figure), becomes zero: $T \cos \alpha - mg = 0.\tag{1}$ After this, the vertical component of the bob's velocity will decrease. Since the bob moves in a circle, according to Newton's second law $mv^2/R = T - mg \cos \alpha.$ Substituting the bob's velocity found from the law of conservation of energy: $mv^2/2 = mgR \cos \alpha$ [assuming release from horizontal position], into this equation, and solving the resulting equation together with equation (1), we find: $\cos \alpha = 1/\sqrt{3}.$ 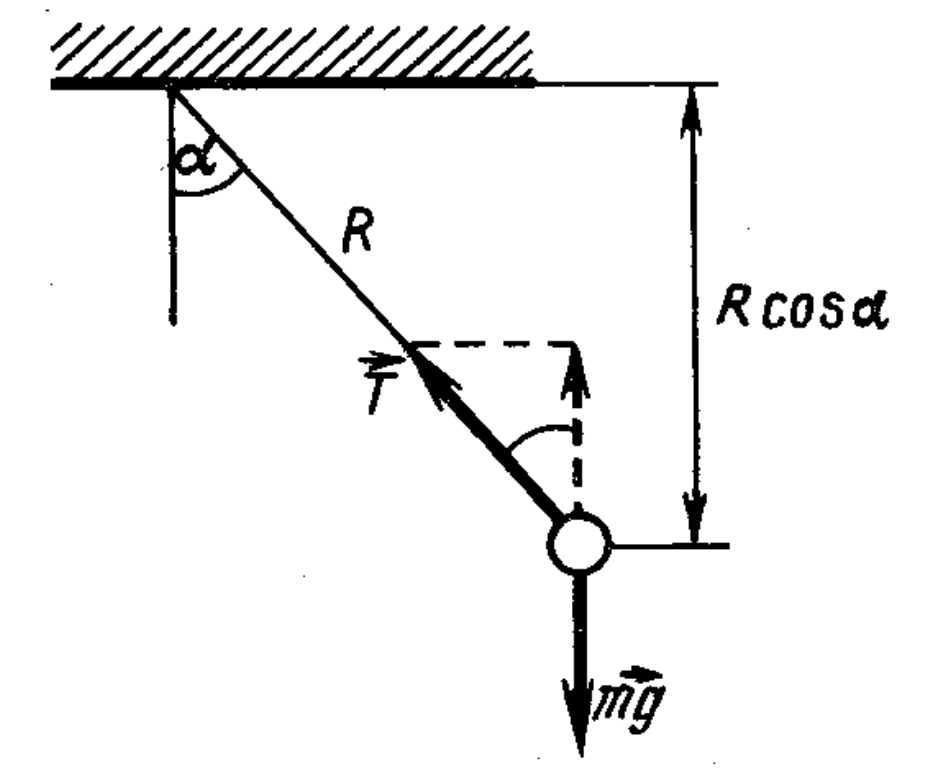
41. Identical elastic balls of mass $m$, suspended on strings of equal length to one hook, are deflected to different sides from the vertical by an angle $\alpha$ and released. The balls collide and bounce off each other. What is the force $F$ acting on the hook:
a) at the extreme positions of the strings;
b) at the initial and final moments of the balls' impact;
c) at the moment of maximum deformation of the balls?
Answer
a) $F = 2mg \cos^2 \alpha$;
b) $F = 2mg (3 - 2 \cos \alpha)$;
c) $F = 2mg$.
Hint
a) The resultant of the string tension force and the ball's weight force is directed perpendicular to the string and imparts an initial acceleration $a = g \sin \alpha$ to the ball.
b) The speed of each ball at the initial moment of impact can be found using the law of conservation of mechanical energy. Then, from the laws of conservation of energy and momentum, it follows (see problems 28 and 39 in Chapter: Conservation of Energy) that the speeds of the balls at the final moment of impact will be equal in magnitude to their speeds at the initial moment of impact and directed in opposite directions. Knowing the speeds of the balls, it is easy to find the tension forces of the strings (see, for example, problem 32).
c) At the moment of maximum deformation of the balls, the speed of each ball is zero.
42. A simple pendulum with a flexible inextensible string of length $l$ is given a horizontal velocity $v_0 = \sqrt{3gl}$ from the equilibrium position. Determine the maximum height $h$ of its rise when moving in a circle, if $v_0^2 = 3gl$. What trajectory will the pendulum bob follow after it reaches the maximum height $h$ on the circle? Determine the maximum height $H$ reached during this motion of the pendulum.
Answer
$h = \sqrt{3}l$; parabolic trajectory (trajectory of a body thrown at an angle to the horizon); $H = 40l/27$.
43. A small ball is suspended at point A on a string of length $l$. At point O at a distance $l/2$ below point A, a nail is driven into the wall. The ball is pulled aside so that the string occupies a horizontal position, and released. At what point in the trajectory does the tension force of the string disappear? How will the ball move further? To what maximum height will the ball rise?
Answer
Below the suspension point by $l/6$; parabolic; $2l/27$ below the suspension point.
Hint
See the previous problem.
44. A vessel, having the shape of an expanding truncated cone with a bottom diameter $D = 20$ cm and a wall inclination angle $\alpha = 60^\circ$, rotates around the vertical axis $OO_1$. At what angular velocity of rotation $\omega$ of the vessel will a small ball lying on its bottom be thrown out of the vessel? Neglect friction.
Answer
$\omega > \sqrt{2g\tan\alpha/D} \approx 13$ rad/s.
Hint
Two forces act on the ball located on the wall of the rotating vessel: the force of gravity $mg$ and the reaction force $N$ of the vessel wall (see figure). At equilibrium of the ball relative to the vessel, the resultant of these forces provides the ball with centripetal acceleration, i.e., $m\omega^2 R = mg \tan \alpha.$ From this, it follows that the ball can be in equilibrium at a distance $R$ from the axis of rotation of the vessel if the vessel rotates with angular velocity $\omega = \sqrt{g\tan\alpha/R}.$ At the bottom of the vessel, the ball is still in equilibrium, but no longer presses on the bottom at $\omega_{cr} = \sqrt{2g\tan\alpha/D};$ if $\omega$ is increased, then from the equation given above, it follows that for no $R \ge D/2$ will it be in equilibrium and will be ejected. 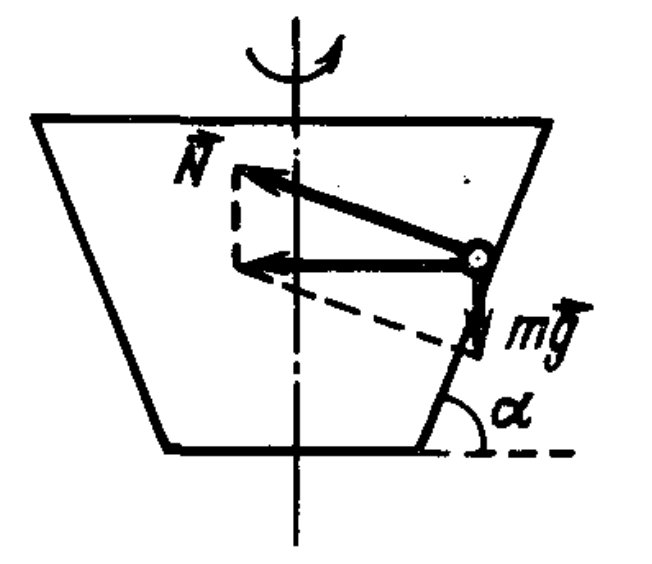
45. A sphere of radius $R = 2$ m rotates uniformly around its axis of symmetry with a frequency of 30 min⁻¹. Inside the sphere, there is a ball of mass $m = 0.2$ kg. Find the height $h$ corresponding to the equilibrium position of the ball relative to the sphere, and the reaction force $N$ of the sphere.
Answer
$h \approx 1$ m; $N \approx 0.4$ N.
Solution
At equilibrium of the ball relative to the sphere, the resultant of the reaction force $N$ of the sphere and the gravity force $mg$ of the ball is directed towards the axis of rotation and provides the ball with centripetal acceleration. The magnitude of this resultant $Q = mg \tan \alpha$ (see figure).
According to Newton's second law $m\omega^2 l = mg \tan \alpha,$ where $l = R \sin \alpha$ is the distance of the ball from the axis of rotation;
$\omega^2 R \sin \alpha = g \tan \alpha.$
This equation has two roots for $\alpha$:
- $\sin \alpha = 0$, $\alpha = 0$;
- $\cos \alpha = g/(\omega^2 R)$.
The position of the ball with $\alpha = \arccos\left(\frac{g}{\omega^2 R}\right)$ is possible only when
$\omega \ge \sqrt{g/R}.$
The position $\alpha = 0$ is possible at any angular velocity of the sphere, but for $\omega < \sqrt{g/R}$ the equilibrium is stable, and for $\omega \ge \sqrt{g/R}$ it is unstable. In our case $\omega > \sqrt{g/R} \approx 2.2 \text{ s}^{-1}$. Height $h = R - R \cos \alpha = R\left(1 - \frac{g}{\omega^2 R}\right)$, and the reaction force of the sphere
$N = mg/\cos \alpha = m\omega^2 R.$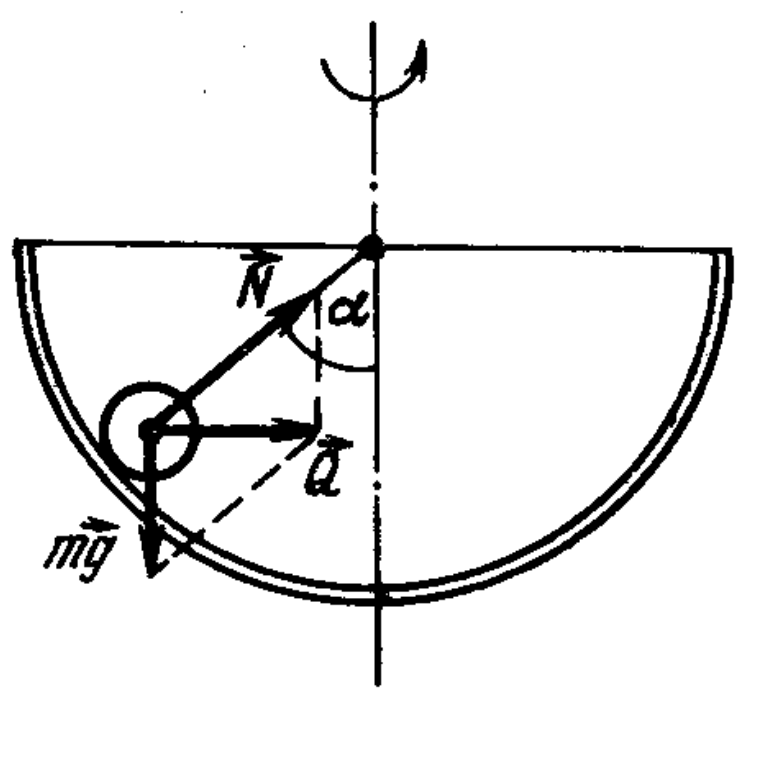
46. Inside a conical surface, moving with acceleration $a$, a ball rotates along a circle of radius $R$. Determine the period $T$ of the ball's motion along the circle. The angle at the apex of the cone is $2\alpha$.
Answer
$T = 2\pi \sqrt{R\tan\alpha/(a + g)}$.
Solution
The forces acting on the ball must provide it with both horizontal and vertical acceleration. Let's resolve the force $F$, acting on the ball from the side of the conical surface, into vertical $F' = F \sin \alpha$ and horizontal $F'' = F \cos \alpha$ components (see figure). The resultant of the vertical component of the force $F'$ and the gravity force provides the ball with acceleration $a$ upwards. The horizontal component of the force $F''$ provides the ball with centripetal acceleration $a_{cp} = \omega^2 R$ ($\omega$ is the angular velocity of rotation). Therefore, according to Newton's second law $ma = F \sin \alpha - mg$ and $m\omega^2 R = F \cos \alpha$. Eliminating $F$ from these equations, we find: $\omega = \sqrt{(a + g)/(R\tan\alpha)},$ $T = 2\pi/\omega = 2\pi \sqrt{R\tan\alpha/(a + g)}.$ 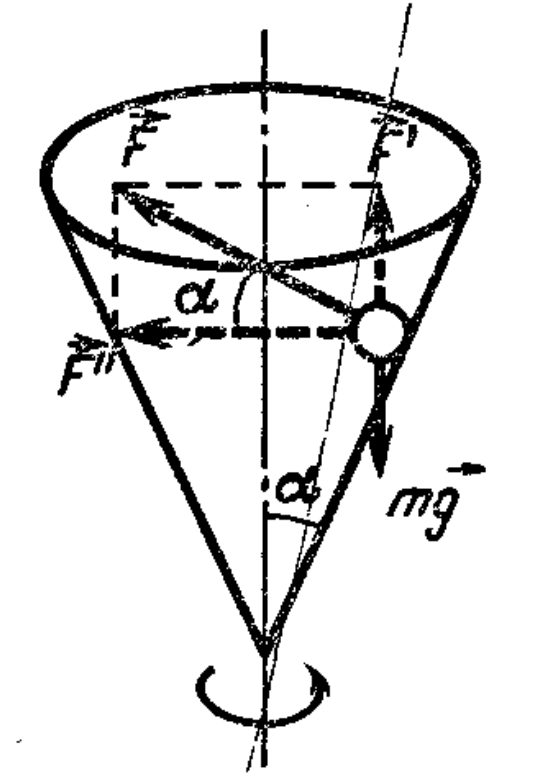
47. A small body of mass $m$ slides down an inclined chute that transitions into a loop-the-loop of radius $R$ (see figure). Friction is negligible. Determine:
a) what must be the minimum height $h$ of the chute so that the body makes a complete loop without falling;
b) what pressure $F$ does the body exert on the support at the point whose radius vector makes an angle $\alpha$ with the vertical?
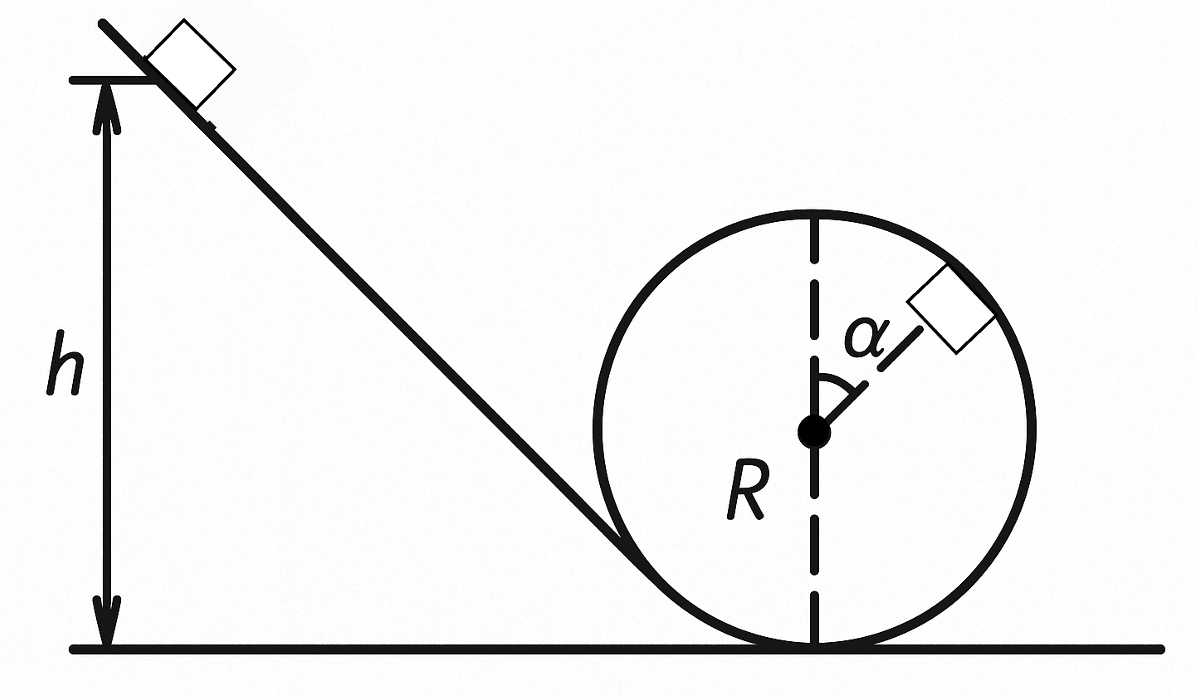
Answer
a) $h = 2.5R$;
b) $F = 3mg (1 - \cos \alpha)$.
Solution
a) The body will not detach from the loop if at the highest point it has a speed $v \ge \sqrt{gR}$ (see problem 37). Writing the law of conservation of energy $\frac{1}{2}mv^2+ mg \cdot 2R = mgh,$ we find that the body must slide down from a height $h = 2.5 R$.
b) At the point whose radius vector makes an angle $\alpha$ with the vertical (see figure), the centripetal acceleration will be provided to the body by the resultant of the reaction force $N$ of the platform and the radial component of the gravity force $(mg)_r = mg \cos \alpha$.
According to Newton's second law
$mv^2/R = N + mg \cos \alpha.$
The speed of the body at this point can be easily determined using the law of conservation of energy:
$\frac{5}{2} mgR = \frac{mv^2}{2} + mg (R + R \cos \alpha),$
$v = \sqrt{gR (3 - 2 \cos \alpha)}.$
Substituting this expression for $v$ into Newton’s second law, we get:
$
N = \frac{m}{R} \left[ gR(3 - 2\cos\alpha) \right] - mg \cos\alpha = 3mg(1 - \cos\alpha)
$
The normal force $F$ exerted by the body on the track numerically equals the normal reaction $N$.
(Determine the value of $N$ for $\alpha = 0$ and $\alpha = \pi$.)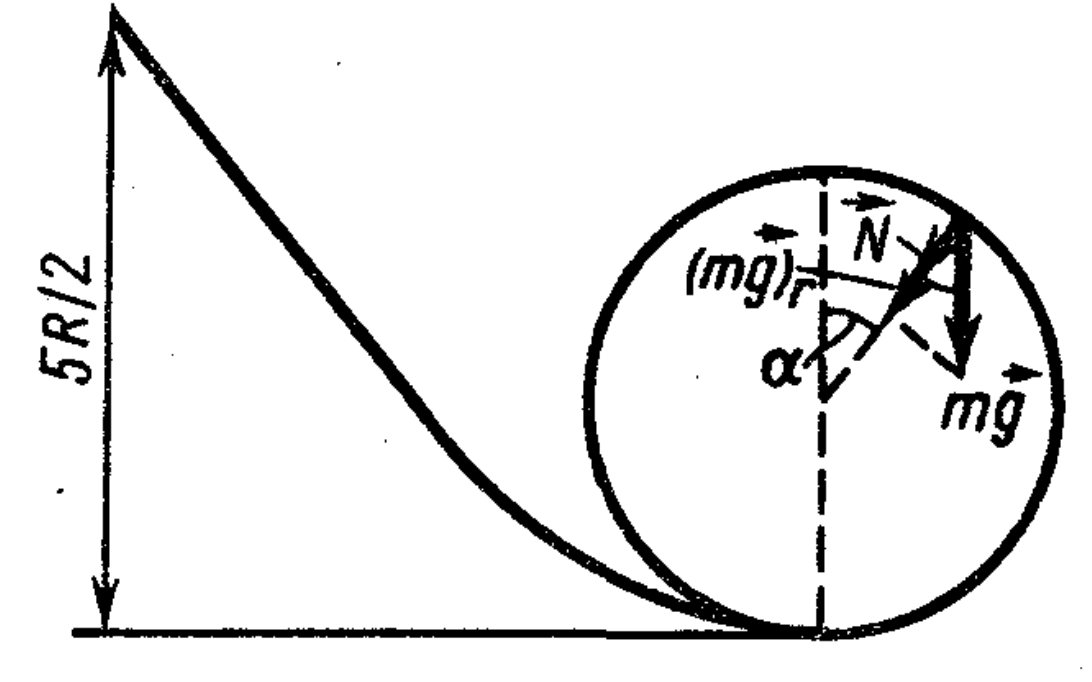
48. A conveyor belt is inclined to the horizontal at an angle $\alpha$. Determine the minimum speed $v_{\text{min}}$ of the belt at which a particle of ore lying on it separates from the surface of the belt at the point where it runs onto the drum, if the radius of the drum is $R$.
Answer
$v_{\text{min}} = \sqrt{gR \cos \alpha}$.
Hint
Separation of the ore from the belt means that the ore has lost contact with the belt and only the force of gravity acts on the ore. Its radial component provides the ore particles with centripetal acceleration at the moment the belt runs onto the drum (see figure) $mv^2/R = mg \cos \alpha.$ 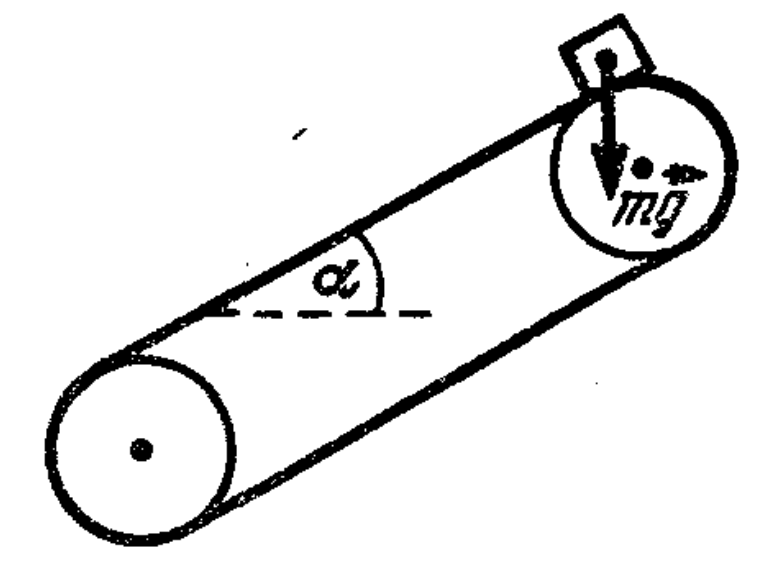
49. A small body slides from the top of a sphere downwards. At what height $h$ from the top will the body detach from the surface of the sphere of radius $R$? Neglect friction.
Answer
$h = R/3$.
Solution
Before detaching from the surface of the sphere, the body is acted upon by its weight $mg$ and the reaction force of the support $N$. The resultant of the radial component of the weight force and the support reaction force provides the body with centripetal acceleration $mv^2/R = mg \cos \alpha - N.$ As the body slides down, the component of the weight force $mg \cos \alpha$ (where $\alpha$ is the angle between the vertical and the direction from the center of the sphere to the body) decreases, and its speed increases, which leads to an even faster decrease in the support reaction force (the support reaction force depends on the nature of the body's motion). At the moment of detachment, $N$ becomes zero and then $mv^2/R = mg \cos \alpha.\tag{1}$ Based on the law of conservation of energy $mv^2/2 = mgh.\tag{2}$ Also, it is obvious that $\cos \alpha = (R - h)/R$. (3) Solving equations (1), (2), (3) together, we get $h = R/3.$
50. Find the kinetic energy of a hoop of mass $m$ rolling with speed $v$. There is no slipping.
Answer
$mv^2$.
Solution
Each point of the hoop participates in two motions: translational motion with velocity $v$ and rotational motion with angular velocity $\omega$ about the center of the hoop. The linear velocity of rotational motion is $v_{rot} = \omega R$. In the absence of slipping $\omega = v/R$ and therefore $v_{rot} = v$. Consider two diametrically opposite identical small elements of the hoop, having mass $\Delta m$ (see figure). Their velocities are equal to the vector sum of the velocities of translational and rotational motions, and therefore: $v_A^2 = v^2 + v_{rot}^2 - 2vv_{rot} \cos \alpha = 2v^2 (1 - \cos \alpha);$ $v_B^2 = v^2 + v_{rot}^2 + 2vv_{rot} \cos \alpha = 2v^2 (1 + \cos \alpha).$ The total kinetic energy of these elements of the hoop is $\frac{\Delta m v_A^2}{2} + \frac{\Delta m v_B^2}{2} = 2 \Delta m v^2.$ This relationship does not depend on $\alpha$, i.e., on the choice of the diameter at the ends of which the chosen elements of the hoop lie. Therefore, the kinetic energy of the entire hoop will be equal to $mv^2$. 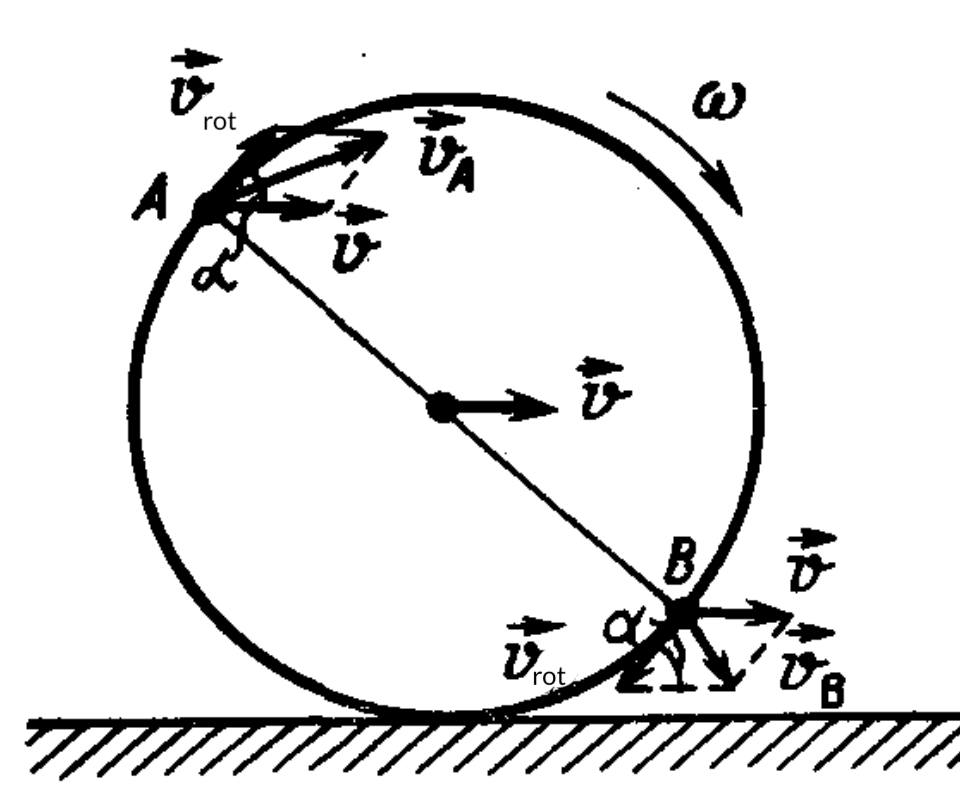
51. A thin hoop rolls without slipping into a pit having the shape of a hemisphere. At what depth $h$ is the normal pressure force of the hoop on the wall of the pit equal to its weight? The radius of the pit is $R$, the radius of the hoop is $r$.
Answer
$h = (R - r)/2$.
Solution
Sliding down, the hoop moves along a circle. Centripetal acceleration is imparted to it by the sum of the radial components of the forces applied to the hoop (see figure), equal to $N - mg \cos \alpha$ ($N$ is the reaction force of the hemisphere, $m$ is the mass of the hoop, and $\alpha$ is the angle formed by the radius vector of the hoop with the vertical). According to Newton's second law $mv^2/(R - r) = N - mg \cos \alpha,\tag{1}$ where $v$ is the velocity of the center of the hoop. From the law of conservation of energy, it follows that $mg(R-r)(1-\cos\alpha) = \frac{mv^2}{2} + \frac{I\omega^2}{2}.$ For a hoop $I=mr^2$. With no slip $v=\omega r$. So $mg(R-r)(1-\cos\alpha) = \frac{mv^2}{2} + \frac{m(v/r)^2 r^2}{2} = mv^2.\tag{2}$ Here $mv^2/2$ corresponds to the kinetic energy of the translational motion of the center of mass of the hoop; $\frac{m(\omega r)^2}{2}$ corresponds to the kinetic energy of rotation of the hoop relative to the center of mass (see previous problem); $mg(R-r)(1-\cos\alpha)$ is the change in potential energy. From equation (2) we find $v^2 = g (R - r) (1-\cos \alpha)$. Substituting this expression for $v^2$ into equation (1) and setting $N = 0$ (condition for detachment), we finally get $\cos \alpha = 1/2$ and $h = (R - r) \cos \alpha = (R - r)/2.$ 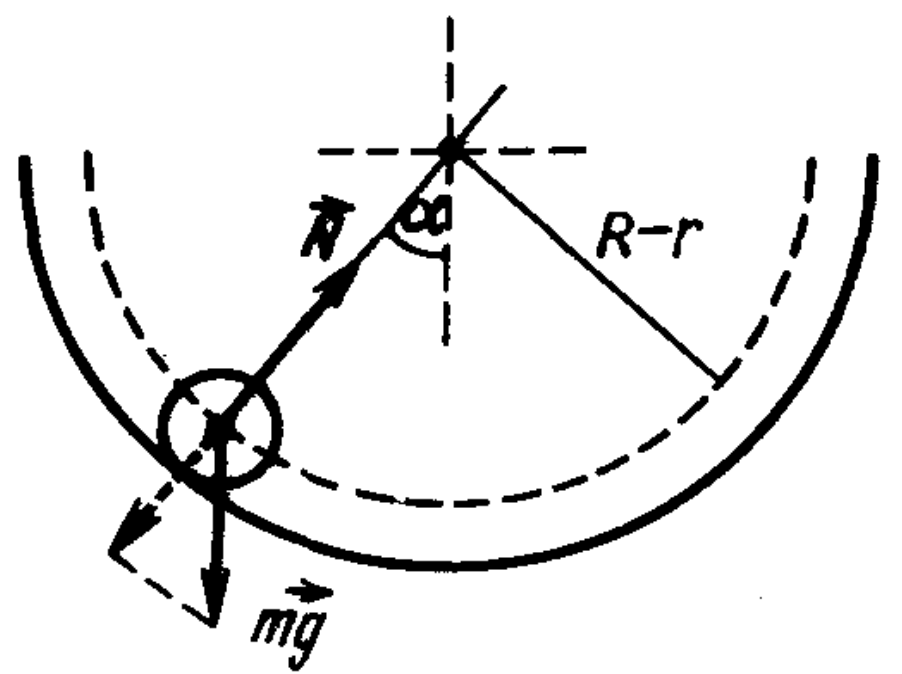
52. A small hoop rolls without slipping on the inner surface of a large hemisphere. At the initial moment, the hoop was at rest at its upper edge. Determine:
a) the kinetic energy of the hoop at the lowest point of the hemisphere;
b) what fraction of the kinetic energy is accounted for by the rotational motion of the hoop around its axis;
c) the normal force pressing the hoop to the lowest point of the hemisphere. The mass of the hoop is $m$, the radius of the hemisphere is $R$.
Answer
a) $mgR$;
b) half;
c) $2mg$.
53. Water flows through a pipe located in a horizontal plane and having a bend of radius $R = 2$ m. Find the lateral pressure of the water. The diameter of the pipe is $d = 20$ cm. $M = 300$ tonnes of water flows through the cross-section of the pipe in one hour.
Answer
$p = \frac{4M^2}{\pi \rho a^3 R t^2} \approx 1.2 \times 10^5$ Pa.
Solution
The centripetal acceleration of the mass of the selected volume of water (see figure) is provided by the force of lateral pressure $F$ from the pipe walls: $mv^2/R = F.$ The force $F$ is equal to the product of the pressure $p$ and the area of the diametral section ABCD, perpendicular to the radius of the ring, i.e., $F = pdl.$ The mass of the selected volume $m = \rho \pi d^2 l / 4.$ The flow velocity of water is determined from the formula $M = \rho \pi d^2 v t / 4\quad (\tex{time } t = 1 \text{ h}),$ whence $v = \frac{4M}{\rho \pi d^2 t}.$ Substituting the values of $m$ and $v$ into the formula for $F$, we get the answer. 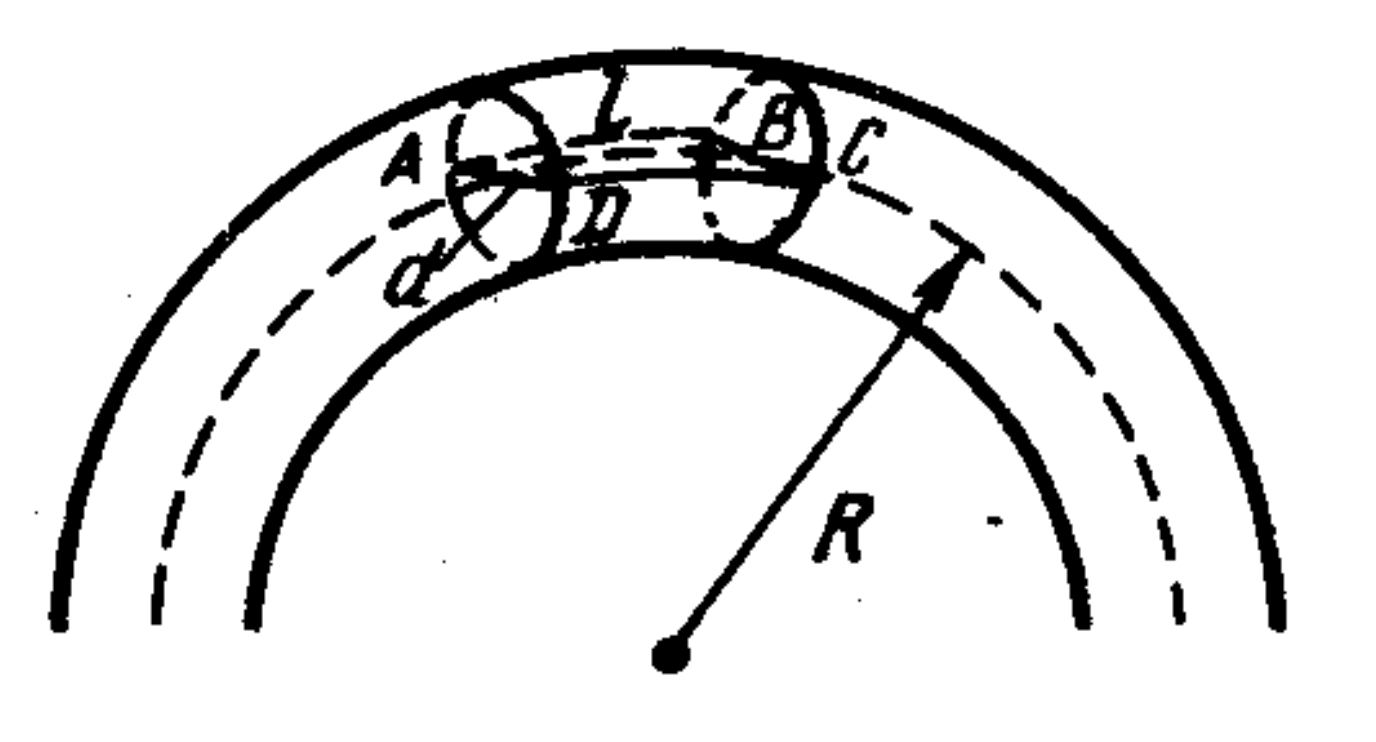
54. A body slides from point A to point B along two inclined surfaces, passing through points A and B once along a convex arc, the second time along a concave one. Both arcs have the same radius of curvature and the coefficient of friction in both cases is the same (see figure). In which case is the speed of the body at point B greater? 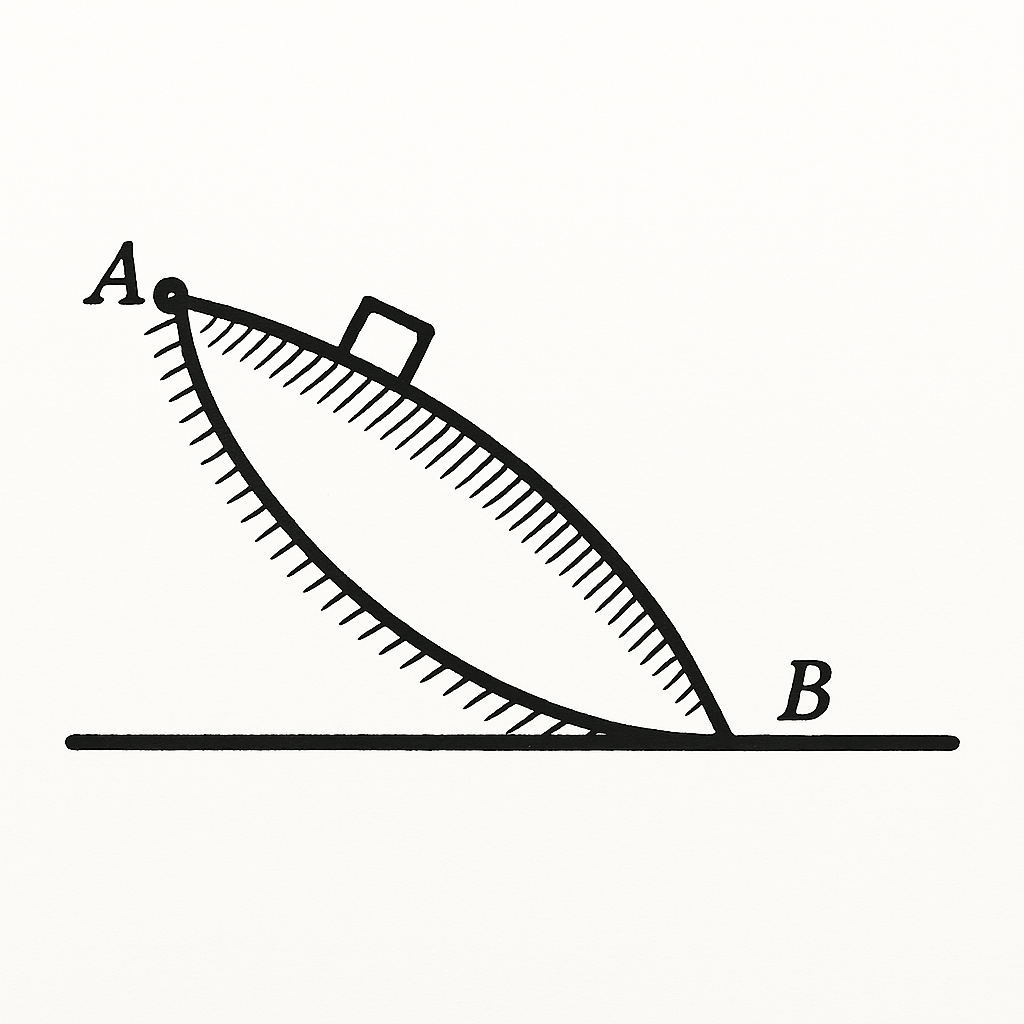
Answer
When moving along a convex arc.
Solution
Indeed, in this case, the pressure of the body on the surface at each point is less than the pressure on the surface at a point located at the same distance from point A, in the case of the body moving along a concave arc (see problem 15). This means that the friction force acting on the body at each point, and consequently, the work done against friction over the entire path, is less than when moving along the concave arc, and the body at point B has a greater kinetic energy in this case.
55. A rod of negligible mass and length $l$ with two small balls $m_1$ and $m_2$ ($m_1 > m_2$) at the ends can rotate about an axis passing through the center of the rod perpendicular to it. The rod is brought into a horizontal position and released. Determine the angular velocity $\omega$ and the pressure force $F$ on the axis at the moment the rod passes through the equilibrium position with the balls.
Answer
$\omega = 2 \sqrt{\dfrac{(m_1 - m_2)g}{(m_1 + m_2)l}}$;
$F = g \dfrac{3(m_1^2 + m_2^2) - 2m_1 m_2}{m_1 + m_2}$.
Solution
The two masses move with the same angular velocity. Let us choose the potential energy reference level at the height where the mass $m_1$ is located at the moment it passes through the equilibrium position. Then, by the law of conservation of energy, we can write: $ (m_1 + m_2)g\frac{l}{2} = m_2 g l + \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 $
Substituting $v_1 = v_2 = \omega \frac{l}{2}$, we find:
$
\omega = 2 \sqrt{ \frac{(m_1 - m_2)g}{(m_1 + m_2)l} }
$
The force $F$ exerted on the axis equals the sum of the tension forces $T_1$ and $T_2$ in each half of the rod. We assume both rods are under tension. Then, according to Newton’s second law:
$
T_1 - m_1 g = m_1 \omega^2 \frac{l}{2}, \quad m_2 g + T_2 = m_2 \omega^2 \frac{l}{2}
$
Substituting the expression for $\omega$ at the moment both masses pass through the equilibrium position and solving these equations for $T_1$ and $T_2$, we obtain:
$
T_1 = \frac{m_1 g}{m_1 + m_2}(3m_1 - m_2), \quad T_2 = \frac{m_2 g}{m_1 + m_2}(m_1 - 3m_2)
$
(When $m_1 < 3m_2$, we get $T_2 < 0$. This means that the half of the rod to which the mass $m_2$ is attached is under compression rather than tension, contrary to our assumption.)
The total force on the axis (assuming both rods are in tension):
$
F = T_1 - T_2 = \frac{3\left(m_1^2 + m_2^2\right) - 2m_1 m_2}{m_1 + m_2} g
$
56. A small ring of mass $m$ is placed on a turn of a cylindrical spiral whose axis is vertical. The ring starts sliding down the spiral without friction. With what force $F$ will the ring press on the spiral after it has completed $n$ full turns? The radius of the turn is $R$, the distance between adjacent turns is $h$ (pitch of the spiral). Assume $h \ll R$.
Answer
$F \approx mg \sqrt{1 + \dfrac{4h^2 n^2}{R^2}}$.
Solution
After making $n$ revolutions, the ring descends by a height $nh$, and from the law of conservation of energy $mghn = \frac{1}{2}mv^2$, it follows that at this point the ring will have a speed: $ v = \sqrt{2ghn} $
This speed is directed tangent to the spiral and can be considered as the sum of a vertical component $v_0$ and a horizontal (rotational) component $v_1$.
In particular:
$
v_1 = v \cos\alpha,
$
where $\alpha$ is the inclination angle of the spiral;
$\alpha \approx \sin\alpha = \frac{h}{2\pi R}$.
Since $h \ll R$, we can take $\cos\alpha \approx 1$ and $v_1 \approx v$.
The horizontal component of the spiral’s reaction force must provide the ring with centripetal acceleration:
$
a_{\text{cp}} = \frac{v_1^2}{R} \approx \frac{2ghn}{R}
$
Therefore, the horizontal reaction force is:
$
F_{\text{hor}} = ma_{\text{cp}} = \frac{2mghn}{R}
$
The ring presses on the spiral with the same force in the horizontal direction.
Thus, the total pressure force $F$ of the ring on the spiral consists of the horizontal component $F_{\text{hor}}$ and the vertical component of gravity, $mg \cos\alpha \approx mg$:
$
F \approx \sqrt{(mg)^2 + \left(\frac{2mghn}{R}\right)^2}
= mg \sqrt{1 + \frac{4h^2 n^2}{R^2}}
$
57. A closed metal chain lies on a smooth horizontal disk, being freely placed on its centering ring, coaxial with the disk. The disk is set into rotation. Assuming the shape of the chain is a horizontal circle, determine the tension force $T$ along the chain if its mass is $m = 150$ g, length $l = 20$ cm, and the chain rotates with a frequency $n = 20$ s⁻¹.
Answer
$T \approx m n^2 l \approx 12$ N.
Solution
Consider a small element of the chain of length $\Delta l = R \Delta \alpha$. The mass of this element $\Delta m = m \Delta l / l = m R \Delta \alpha / l.$ During the rotation of the chain, the centripetal acceleration is imparted to the selected element by the tension forces acting on it from the rest of the chain. The resultant of these forces is $2T \sin (\Delta \alpha / 2)$ (see figure).
According to Newton's second law
$2T \sin (\Delta \alpha / 2) = (\Delta m) \omega^2 R.$
Substituting $\omega = 2\pi n$ here and taking into account that for small angles $\sin (\Delta \alpha / 2) \approx \Delta \alpha / 2$, we get
$2T \Delta \alpha / 2 \approx m R^2 \Delta \alpha (2\pi n)^2 / l,$
whence $T \approx m n^2 (2\pi R)^2 / l = m n^2 l.$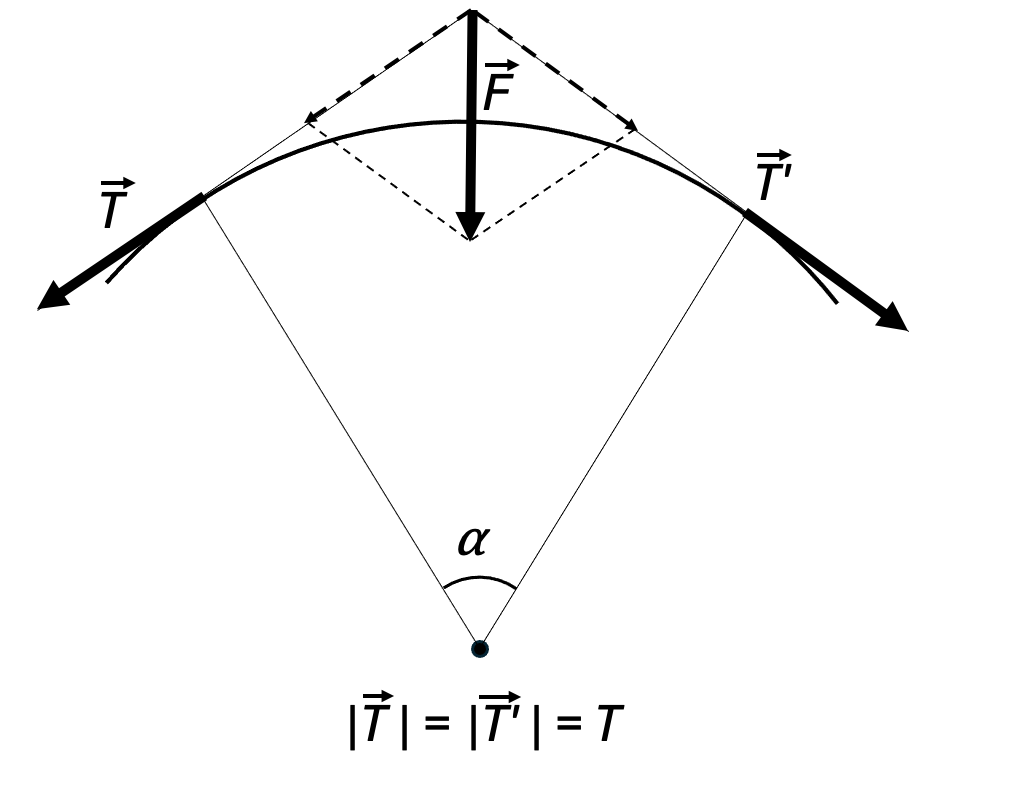
58. A jet airplane $m = 30$ t flies along the equator from west to east with a speed $v = 1800$ km/h. By how much will the lift force acting on the airplane change if it flies with the same speed from east to west?
Answer
$\Delta F_{lift} \approx 1.74 \times 10^3$ N.
Solution
The resultant of the gravity force of the aircraft and the lift force $F_{lift}$ provides it with centripetal acceleration. When moving from west to east, the velocities of the aircraft and the Earth add up. Therefore, we can write $m (\omega R + v)^2 / R = mg - F_{1lift}\tag{1}$ where $\omega$ is the angular velocity of the Earth; $R$ is its radius. If the aircraft flies in the opposite direction, then $m (\omega R - v)^2 / R = mg - F_{2lift}. \tag{2}$ From equations (2) and (1) we find the change in lift force: $\Delta F_{lift} = F_{2lift} - F_{1lift} = 4mv\omega = 4m (2\pi v / T),$ where $T$ is the period of rotation of the Earth, i.e., one day.