Let us now take up the question of physical observations in an accelerating bus or streetcar. A peculiarity of this example distinguishing it from the preceding one consists in the following. In the example with the elevator, the additional weight and the Earth’s gravitation were directed along a single line. In a decelerating or accelerating streetcar, the additional weight is directed at right angles to the Earth’s gravitation. This induces distinctive, although customary, sensation in the passenger. If the streetcar increases its speed, there arises an additional force opposite in direction to that of motion.

Let us add this force to that of the Earth’s gravitation. The resultant force acting on a person in the car will be directed at an obtuse angle to the direction of the motion. Standing, as usual, face forward in the car, we sense that our “upwards” has moved. In order not to fall, we shall want to become “vertical”—as shown in Figure 1 (a). Our “vertical” is slanting. It is inclined at an acute angle to the direction of the motion. If a person stands at right angles to the motion without holding on to any- thing, he will be sure to fall backwards.

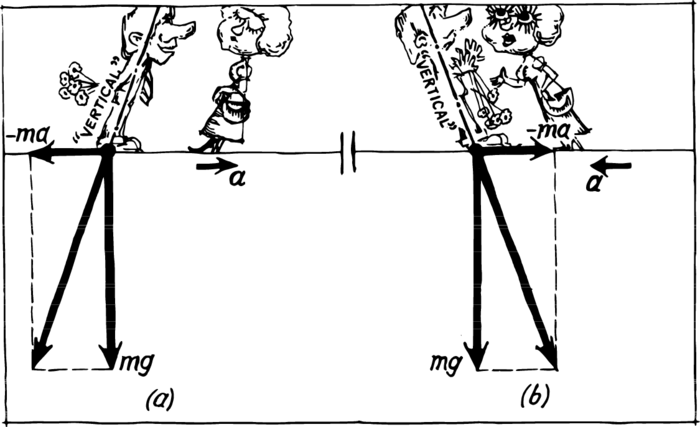
Finally, the motion of the streetcar becomes uniform, and we can stand calmly. However, we are drawing close our to the next stop. The driver applies the brakes and “vertical” is deviating. It is now directed, as can be seen from the drawing in Figure 1 (b), at an obtuse angle to the motion. In order not to fall, the passenger leans backwards. However, he won’t remain long in such a position. The car comes to a halt, the deceleration disappears, and the “vertical” is now directed at right angles to the Earth. The position of one’s body must again be changed. Check your sensations. Isn’t it true that when the deceleration began you seemed to be pushed from behind, and when the car came to a halt you seemed to be pushed in your chest.

Similar phenomena also occur when a streetcar moves around a curve. We know that motion around a circle, even with a constant speed, is accelerated. The faster the streetcar moves and the smaller the radius of curvature \(R\), the greater the acceleration \(v^{2} /R\). The acceleration of such a motion is directed along a radius towards the centre. But this is equivalent to the appearance of an additional force directed outwards from the centre. Therefore, an additional force of \(mv^{2}/R\) will be acting on a streetcar passenger during a turn throwing him out towards the external side of the curve. The radial force \(mv^{2}/R\) is called centrifugal. We have already met this force before (true, considered from a somewhat different point of view).

The action of a centrifugal force during the turning of a streetcar or a bus can only lead to a slight unpleasantness. The force \(mv^{2}/R\) is not large in this case. However, during a speedy motion around a curve, the centrifugal force can become great enough to pose a threat to one’s life. Pilots come across large values of \(mv^{2}/R\) when their airplanes “loop-the-loop”. While the airplane is describing a circle, the centrifugal force acts on the pilot pinning him to his seat. The smaller the circumference of the loop, the greater the additional force with which the pilot is pinned to the seat. If this “weight” becomes large enough, a person can be “torn” because tissues of living organism possess limited strength and cannot withstand an arbitrary weight.

But how much weight can a person “put on” without seriously endangering his life? That depends on the duration of the overload. If it lasts a fraction of a second, a person is capable of withstanding an overload from \(7g\) to \(9g\). During ten seconds a pilot can withstand an overload from \(3g\) to \(5g\). Cosmonauts are interested in the kind of overload a person is able to bear for tens of minutes and even, perhaps, hours. In such cases, it is likely that the overload should be considerably lighter.

Let us compute the radii of a loop which an airplane flying at various speeds can describe without any danger to the pilot. We shall use the acceleration \(v^{2}/R = 4g\). Then \(R = v^{2}/4g\), and for a speed of 360 km/h = 100 m/s the radius of the loop is 250 m. But if the speed is four times greater, i.e. 1440 km/h (and such speeds have already been surpassed by modern jet airplanes), the radius of the loop should be increased by a factor of 16. The minimum radius of the loop becomes equal to 4 km.

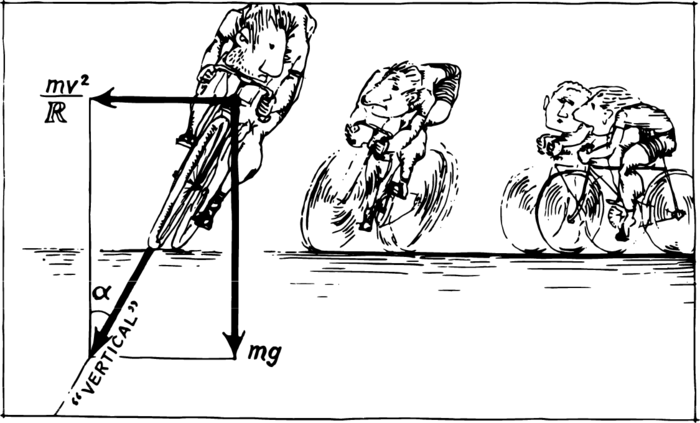
Nor shall we leave a more modest form of transportation—the bicycle—without attention. Everyone has seen how a cyclist inclines while rounding a turn. Let us suggest to a cyclist that he should ride around a circle of radius \(R\) with speed \(v\), i.e. move with an acceleration \(v^{2} / R\) directed towards the centre. Then besides the Earth’s gravitation an additional centrifugal force directed horizontally outwards from the centre of the circle will act on the cyclist. These forces and their sum are shown in Figure 2. It is clear that the cyclist should hold himself “vertically”, or else he will fall down. But … his vertical does not coincide with that of the Earth. It can be seen from the figure that the vectors \(mv^{2}/R\) and \(mg\) are the legs of a right triangle.

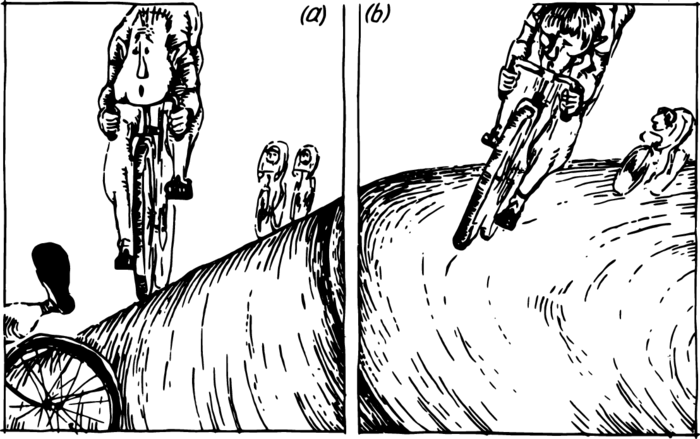
The ratio of the leg opposite angle \(\alpha\) to the adjacent one is called the tangent of angle \(\alpha\) in trigonometry. We have \(\tan \alpha = v^{2} /R g\); the mass has been cancelled out in full agreement with the equivalence principle. Hence, the cyclist’s angle of inclination does not depend on his mass-both a stout and a thin riders must incline identically. The formula and the triangle drawn in the figure show the dependence of the incline on the speed of motion (it grows as the latter increases) and the radius of the circle (it increases as the latter decreases). We have explained why the vertical of the cyclist does not coincide with that of the Earth. What then will he feel? We must rotate Figure 2 in order to find it out. The road now looks like the slope of a mountain (Figure 3 (a)), and it becomes clear to us that if the force of friction between the tires and the asphalt is insufficient (for example, when the road is wet), the bicycle may slip and a sharp turn may end with a fall into a ditch.

In order to forestall this, highways are built with sharp turns inclined, i.e. horizontal for a cyclist—as shown in Figure 3 (b). In this way, the tendency to slip can be greatly diminished, or even entirely eliminated. This is precisely how turns are constructed in bicycle tracks and superhighways.