If a point moves around a circle, the motion is accelerated, if only because the velocity is changing its direction all the time. The speed may remain constant, and we shall confine our attention to precisely such a case.

We shall draw the velocity vectors at successive time intervals and transfer their initial points to a single point. (We have the right to do this.) If a velocity vector is rotated through a small angle, the change in velocity, as we know, will be represented by the base of an isosceles triangle. Let us construct the changes in velocity during the course of a complete revolution of the body (Figure 1).

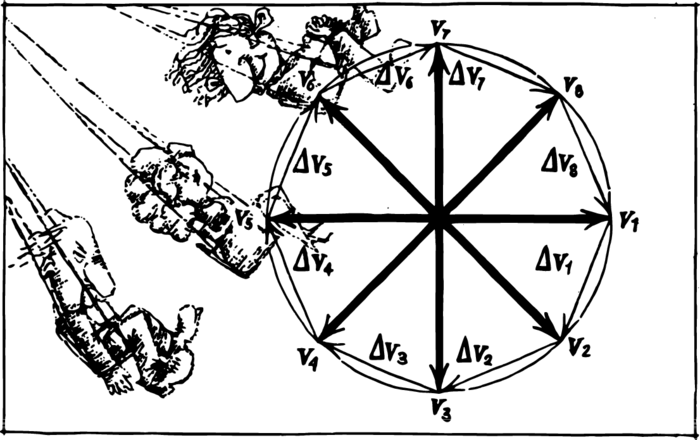
The sum of the magnitudes of the changes in velocity during a complete revolution will be equal to the sum of the sides of the depicted polygon. In constructing each small triangle, we have implicitly assumed that the velocity vector changed by jumps, but its direction is actually changing continuously. It is perfectly clear that the smaller we take the vertex angles of the small triangles, the less will be our error. The smaller the sides of our polygon, the closer will they cling to the circle of radius \(v\). Consequently, the exact value of the sum of the magnitudes of the changes in velocity during the course of the revolution of a point will be the circumference \(2\pi v\) of the circle. The magnitude of the acceleration is found by dividing it by the time of a complete revolution \(T\): \[a = \frac{2\pi v}{T}\]

The time of a complete revolution in motion around a circle of radius \(R\) can be expressed in the form \(T = 2 \pi R/v\). Substituting this expression in the preceding formula, we obtain the following for the acceleration: \(a = v^{2}/R\).

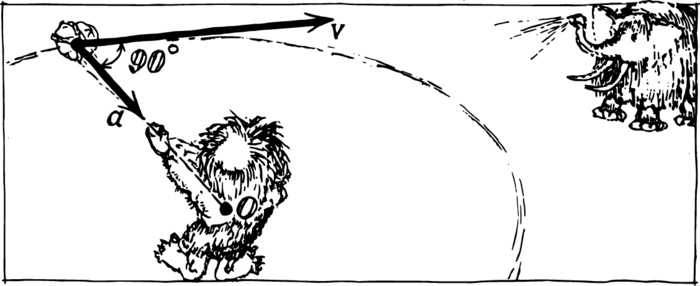
For a constant radius of rotation, the acceleration is proportional to the square of the speed. For a given speed, the acceleration is inversely proportional to the radius. This same reasoning shows us how the acceleration of a circular motion is directed at each given instant. The smaller the vertex angle of the isosceles triangles which we used for our proof, the nearer the angle between the increment in velocity and the velocity will be to 90°.

Therefore, the acceleration of a uniform circular motion is directed perpendicular to the velocity; and how are the velocity and acceleration directed relative to the trajectory? Since the velocity is tangent to the path, the acceleration is directed along the radius towards the centre of the circle. These relationships are clearly seen in Figure 2.

Try to twirl a stone on a string. You will clearly feel the need for muscular exertion in order to do this. And why is force necessary? After all, isn’t the body moving uniformly? The whole point here is that it isn’t! The body is moving with a constant speed, but the continuous change in the direction of the velocity makes this motion accelerated. Force is necessary in order to deflect the body from an inertial straight path. Force is needed in order to create the acceleration \(v^{2}/R\), which we have just computed.

According to Newton’s law, force is always pointed in the direction of the corresponding acceleration. Consequently, a body revolving around a circle with a constant speed should be subject to the action of a force directed along a radius towards the centre of the circle. The force acting on the stone exerted by the string is called centripetal; it is just this force that supplies the acceleration \(v^{2}/R\). Hence, the magnitude of this force is \(m v^{2}/R\).

The string pulls the stone; the stone pulls the string. In these two forces we recognize “an object and its mirror image”—forces of action and reaction. The force with which the stone acts on the string is frequently called centrifugal. The centrifugal force is, of course, equal to \(m v^{2}/R\) and directed along the radius out from the centre of the circle. The centrifugal force acts on the body counteracting the tendency of the revolving body to move rectilinearly.

What we have said applies also to the case when the role of the string is played by gravity. The Moon revolves around the Earth. What is it that retains our satellite? Why doesn’t it go off, following the law of inertia, in an interplanetary trip? The Earth is holding on to the Moon with an “invisible string”—a gravitational force. This force is equal to \(m v^{2}/R\), where \(v\) is the speed of the motion along the lunar orbit, and \(R\) is the distance to the Moon. The centrifugal force in this case acts on the Earth, but, because of the Earth’s great mass, it only slightly influences the character of our planet’s motion.

Suppose that it is required to send an artificial Earth satellite into a circular orbit at a distance of 300 km from the Earth’s surface. What should be the speed of such a satellite? At a distance of 300 km, the acceleration of free fall is somewhat less than on the surface of the Earth, and is equal to \(8.9~\mathrm{m/s^2}\). The acceleration of a satellite moving in a circle is equal to \(v^{2}/R\), where \(R\) is the distance from the centre of the circle (i.e. from the centre of the Earth)—about \(6,600~\mathrm{km} = 6.6\times 10^6~\mathrm{m}\). On the other hand, this acceleration is equal to the acceleration of free fall, \(g\). Consequently, \(g = v^{2}/R\), from which we find the speed of the satellite’s orbital motion: \begin{align} v & = \sqrt{gR} = \sqrt{8.9 \times 6.6\times 10^6} \\ & = 7700~\mathrm{m/s} = 7.7~\mathrm{km/s} \end{align} The minimum speed necessary for a body thrown horizontally to become an Earth satellite is called the orbital velocity. It is clear from the example we have given that this speed is close to 8 km/s.