In mathematics we need to refer to some certain sets of numbers so often that we denote them by special symbols (in particular by \(\mathbb{N},\mathbb{Z},\mathbb{Q},\mathbb{R}\) , and \(\mathbb{C}\) ). These double struck letters (sometimes called blackboard bold letters) are used to distinguish these specific sets (defined below) from some other sets that happen to be denoted by the the same letters, for example by \(R\) .
The most common numbers are the numbers 1, 2, 3,... which are used for counting are called natural numbers or positive integers . The set of all natural numbers is often denoted by \(\mathbb{N}\) \[\mathbb{N}=\{1,2,3,...\}\]
- The three dots, known as an ellipsis, signify that the pattern continues indefinitely.
The numbers \(-1,-2,-3,...\) are called negative integers. The set of all integers (positive and negative and zero) is denoted by \(\mathbb{Z}\) (standing for the German word Zahlen that means “numbers”): \[\mathbb{Z}=\{...,-3,-2,-1,0,1,2,3,...\}\] which can also be written as \[\mathbb{Z}=\{0,\pm1,\pm2,\pm3,\pm4,...\}.\]
A rational number is a number that can be written as a fraction, or quotient, of two integers. For example, \(-3/4\) is a rational number. All integers are rational numbers because they can be written as a fraction with denominator 1; for example, \(-3\) can be written as \(-3/1\) . Other examples of rational numbers include numbers that have decimal representations that either terminate (for example \(3.89\) can be written as \(389/100\) ) or do not terminate but have repeating blocks of digits (for example \(0.3333...\) is the same as \(1/3\) ). The set of all rational numbers is denoted by \(\mathbb{Q}\) \[\mathbb{Q}=\left\{ \left.\frac{p}{q}\right|\ p,q\in\mathbb{Z}\right\} .\]
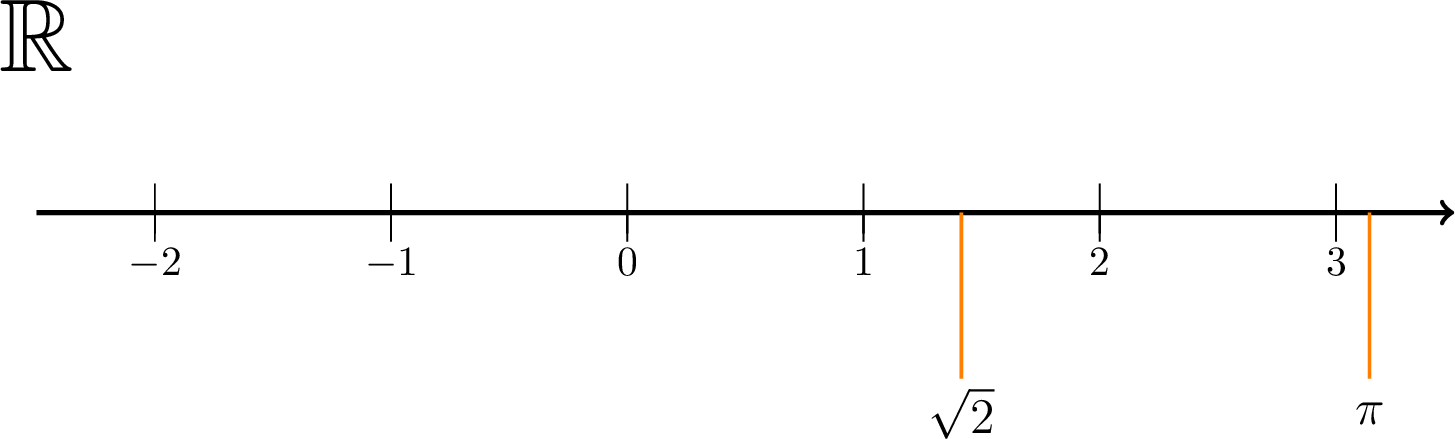
The ancient Greeks knew that the lengths of some lines in simple figures cannot be expressed as the ratio of integers. For example, from the Pythagorean theorem they knew that the diagonal of a square with sides of unit length is \(\sqrt{2}\) , but \(\sqrt{2}\) cannot be written in the form of \(p/q\) where \(p\) and \(q\) are integers. Another well-known example that cannot be expressed as the ratio of two integers is \(\pi=3.141592\ldots.\) Such numbers are called irrational numbers . The decimal digit representation of an irrational number goes on forever and never repeats. The set of all rational and irrational numbers is called the set of real numbers and is denoted by \(\mathbb{R}\) .
- Note that \[\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}\subset\mathbb{R}.\]
The set of all numbers in the form \(a+ib\) where \(a\) and \(b\) are real numbers and \(i=\sqrt{-1}\) is called the set of complex numbers and is denoted by \(\mathbb{C}\) \[\mathbb{C}=\{a+ib|\ a,b=\mathbb{R}\}.\]
Why is \(\sqrt{2}\) irrational?
Geometric Interpretation of Real Numbers as Points on a Line
Real numbers can be visualized on a straight line called the real number line or real line . Each real number corresponds to a unique point on the line, and each point on the real line corresponds to a unique number.
The geometric representation of real numbers as points on a straight line is a familiar concept. In this representation, a specific point is designated as 0, while another point to its right is chosen to represent 1, as illustrated below. This selection establishes the scale for the line. Positive numbers lie to the right of the origin (0), while negative numbers lie to the left. The point twice the distance from 0 to 1 is labeled 2, while the point the same distance to the left of 0 is labeled \(-1\) , and so on. This way, every real number corresponds to a unique point on the line, and conversely, every point on the line corresponds to a unique real number, called its coordinate . Because of this one-to-one correspondence, the line is often referred to as the real number line or the real line , and it’s customary to use the terms "real number" and "point" interchangeably. We often say "the point \(x\) " instead of specifying "the point corresponding to the real number \(x\) ."
Basic Rules of Algebra
Basic properties of the fundamental operations— addition, subtraction, multiplication and division — that are often called the basic rules of algebra are summarized in the following table. These properties are true for real numbers, variables, and algebraic expressions.
| Name | Math | Description | Example |
|---|---|---|---|
| Commutative Property of Addition | \(a+b=b+a\) | We can add numbers in any order | \(2+3=3+2\) \[4+2x=2x+4\] |
| Commutative Property of Multiplication | \(ab=ba\) | We can multiply in any order | \(2\cdot3=3\cdot2\) \[x\cdot4=4\cdot x\] |
| Associative Property of Addition | \(a+(b+c)=(a+b)+c\) | We can group numbers in a sum any way we want and get the same answer. | \(2+(3+5)=(2+3)+5\) \[x+(5+7)=(x+5)+7\] |
| Associative Property of Multiplication | \(a(bc)=(ab)c\) | We can group numbers in a product any way we want and get the same answer. | \(2\cdot(3\cdot4)=(2\cdot3)\cdot4\) \[(-4y)\cdot x=-4(yx)\] |
| Distributive Property | \(a(b+c)=ab+ac\) \[a(b-c)=ab-bc\] | We can distribute multiplication over all terms of the sums or differences within parentheses | \(2\cdot(3\pm7)=2\cdot3\pm2\cdot7\) \[x\cdot(3\pm5)=3x\pm5x\] |
| Additive Identity Property | \(a+0=0+a=a\) | Adding zero to any number yields the same number | \(2+0=0+2=2\) \[3x+0=0+3x\] |
| Multiplicative Identity Property | \(a\cdot1=1\cdot a=a\) | Multiplying any number by 1 yields the same number | \(3\cdot1=1\cdot3=3\) \[1\cdot x=x\] |
| Additive Inverse Property | \(a+(-a)=0\) | If we add a number and its opposite, we will get 0 | \(3+(-3)=0\) \[2x+(-2x)=0\] |
| Multiplicative Inverse Property | \(a\cdot\dfrac{1}{a}=1\quad(a\neq0)\) | If we multiply a nonzero number and its reciprocal, we will get 1 | \(3\cdot\dfrac{1}{3}=1\) \[(x+1)\cdot\dfrac{1}{x+1}=1\] \[(\text{if }x\neq-1)\] |
Here are some properties of real numbers:
The product of any number and 0 is 0 \[0\cdot a=0\qquad\text{for all }a.\]
Proof
We know \[\begin{align} a=a\cdot 1&=a\cdot (1+0)\\ &=a\cdot 1 + a\cdot 0\\ & = a +a\cdot 0 \end{align}\] Comparing \(a=a+a\cdot 0\) and \(a=a+0\) , we conclude that \(a\cdot 0 =0\) .
- Note that \(0\) has no multiplicative inverse because if \(1/0 = b\) , it would imply \(1 = 0 \cdot b\) , but \(0 \cdot b = 0 \neq 1\) . This demonstrates that we cannot assign a definite value to \(1/0\) . Therefore, division by zero is not a valid operation , and if \(a\) is any number, \(a/0\) has no meaning.
- If \(a\neq0\) , then \(\dfrac{0}{a}=0\) because \(a\cdot0=0\) . (again \(a/0\) has no meaning).
Zero-Product Property
If \(ab=0\) , then either \(a=0\) or \(b=0\) (or both equal \(0\) ).
Proof
We consider two cases. If \(a=0\) then there is nothing more to prove. However, if \(a\neq 0\) , then \(a^{-1}\) exists and we can multiply both sides of the equation by \(a^{-1}\) , giving \(b=0\cdot a^{-1}=0\) .