Consider a particle which is free to move in any direction, and which is held in equilibrium by some general system of forces whose resultant is zero. In Fig. 1 one of the forces of the system, \(\mathbf{F}\), is shown, along with its three rectangular components.

We now imagine that the particle is given some arbitrary infinitesimal displacement \(\delta \mathbf{s}\). This displacement is arbitrary in the sense that it can be in any direction.

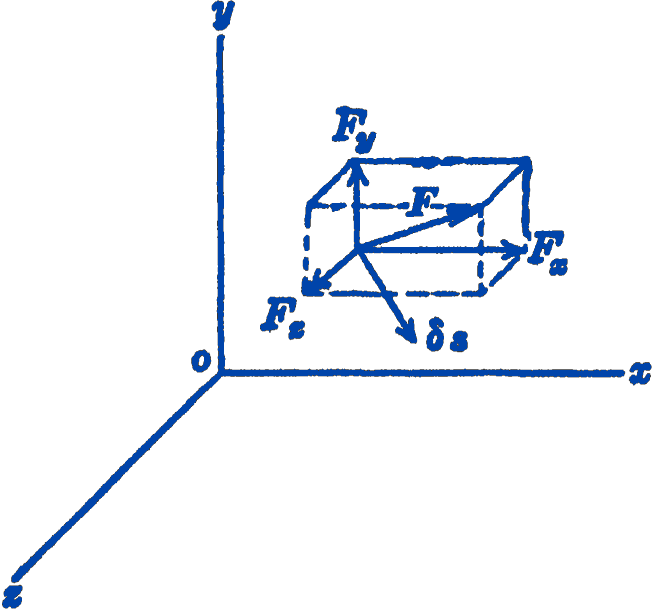
We next compute the work \(\delta W\) which is done by the force \(\mathbf{F}\) during the displacement \(\delta s\). This work \(\delta W\) is the scalar product of \(\mathbf{F}\) and \(\delta \mathbf{s}\). \[ \delta W=\mathbf{F} \cdot \delta \mathbf{s}. \]

For all of the forces in the system: \[ \delta W=\sum F \cdot \delta \boldsymbol{s}. \]

Writing this in terms of components along a system of rectangular coordinates, we have: \[ \begin{aligned} \delta W&=\sum\left(F_{x}\,\mathbf{i}+F_{y}\,\mathbf{j}+F_{z}\, \mathbf{k}\right) \cdot(\delta x\, \mathbf{i}+\delta y\, \mathbf{j}+\delta z\, \mathbf{k}) \\ \delta W&=\sum\left(F_{x} \delta x+F_{y} \delta y+F_{z} \delta z\right)\\ &=R_{x} \delta x+R_{y} \delta y+R_{z} \delta z \end{aligned} \] where \(R_{x}, R_{y}\), and \(R_{z}\) are the rectangular components of the resultant of the system.

If we consider the case in which the forces acting on the particle form a system in equilibrium, we have: \(R_{x}=0 ; R_{y}=0 ; R_{z}=0\). Thus \(\delta W=0\), for any values of \(\delta x, \delta y, \delta z\).

We next examine the conditions under which the converse statement is true, i.e., the conditions under which the statement \(\delta W=0\) is both necessary and sufficient for the equilibrium of the system. It will be seen that the only case in which \(\delta W=0\) would not be sufficient to insure equilibrium would be that in which one of the displacement components would be zero. If, for example, \[ \delta x \neq 0 ; \quad \delta y \neq 0 ; \quad \delta z=0 \] then \(\delta W\) could be zero in the presence of a force component \(F_{z}\). If, however, in our definition of the displacement \(\delta s\) we require that \(\delta x, \delta y\), and \(\delta z\) be all different from zero, which we imply by the word “arbitrary,” then the expression \(\delta W=0\) becomes both necessary and sufficient for the equilibrium of a particle.

We therefore define a virtual displacement of a free particle as any arbitrary, infinitesimal displacement for which \(\delta x, \delta y\), and \(\delta z\) are different from zero. We use the notation \(\delta \mathbf{s}\) instead of \(d\mathbf{s}\) to indicate that the displacement is arbitrary, and can be taken in any direction.

The principle of virtual displacements¹ thus states that the condition for the equilibrium of a free particle is that the work done upon any virtual displacement of the particle should be equal to zero. \[ \delta W=\sum\left(F_{x} \delta x+F_{y} \delta y+F_{z} \delta z\right)=0 \] The quantity \(\delta W\) is called the virtual work of the system, and the above principle is often called “the principle of virtual work.”