We define the potential energy of a system¹ as follows: The change in the potential energy of a system which is moved from one configuration \(A\) to another configuration \(B\) is the negative of the work which is done by the forces of the system as the system is moved from \(A\) to \(B\).

We can define a potential energy \(V\) only for those cases in which the forces acting on the system are functions only of the position of the system and are independent of the path followed by the system on going from one configuration to another. Consider the two situations shown in Fig. 1.

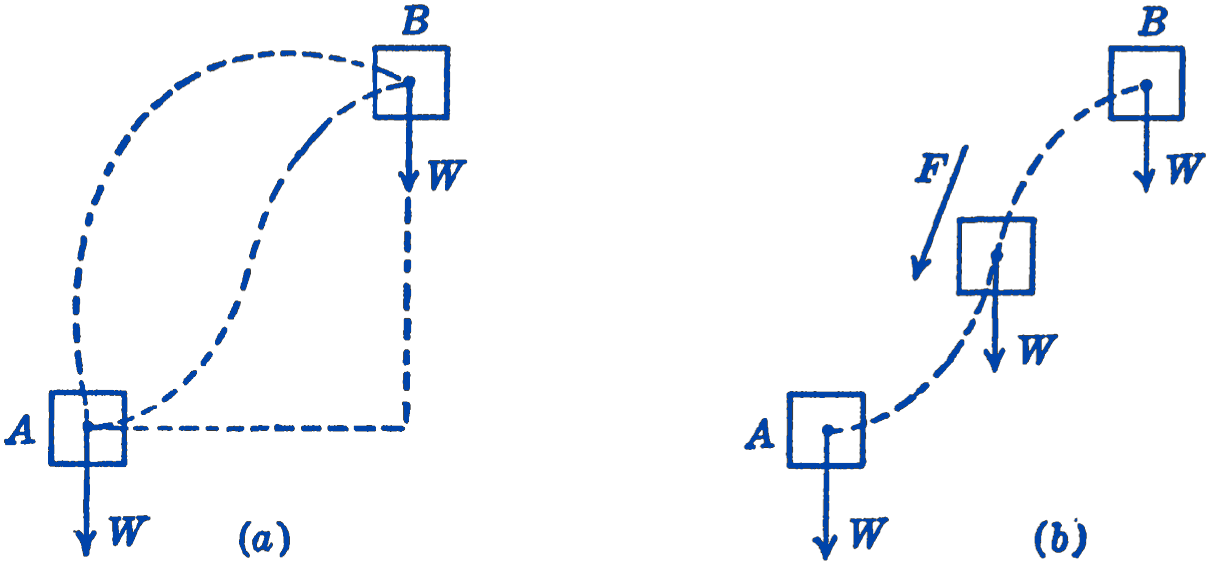
In Fig. 1a we have shown a system acted upon only by gravity forces. The total work done by the forces during the motion from \(A\) to \(B\) will be independent of the path that is followed and will depend only upon the locations of the points \(A\) and B. In Fig. 1b, we have added air resistance forces to the system. In this case the work done will depend upon the path chosen, since more work would be done for a longer path. The air resistance forces would also increase as the velocity of the body increases, so that the work done would thus also depend upon velocity. It will be seen that it is possible to define a potential energy as a unique determinate quantity only for cases such as (a). Such systems are said to be conservative systems. Systems of the type shown in (b), in which there are such effects as frictional dissipations which make it impossible to define a potential energy, are called non-conservative systems. We shall restrict ourselves in the following discussion to conservative systems.

With the above definition of a potential energy, the condition that the virtual work should disappear for an equilibrium position can thus also be stated as \[ \delta V=0 \] i.e., for equilibrium of a force system the potential energy has a stationary value. Under various conditions, this stationary value might be a minimum, a maximum, or a point of inflection. We will now investigate the physical significance of these different possibilities.