The Principle of Virtual Displacements

In general, I believe that I may assert that all the general principles which may still be discovered in the science of equilibrium will be only this same principle of virtual velocities, looked at from different points of view, and differing from it only in the form of statement.—Lagrange, Mécanique Analytique (1788).

In the development of the principles of statics outlined in the preceding pages, we have adopted only one of several possible points of view concerning the basic elements of the subject. In considering such a problem as the equilibrium of two weights, Fig. 1a, we have emphasized the fact that the significant quantities involved are the magnitudes \(W_{1}\) and \(W_{2}\) of the forces and the distances \(a\) and \(b\) of the forces from the pivot point. The development of these ideas, starting with Archimedes, and brought to their modern form by Varignon, finally culminated in the concept of the moment of a force about a point. In the problem of Fig. 1, this concept of a moment would lead to the following equilibrium equation: \(\left(W_{1}\right)(a)=\left(W_{2}\right)(b)\). It was perceived, however, by Galileo and Stevinus, that it would be just as logical to focus the attention upon another significant quantity. Suppose (Fig. 1b) that we imagine that the lever and weight system has tipped through some small angle, thus raising \(W_{1}\) through a distance \(c\) and lowering \(W_{2}\) through a distance \(d\). From similar triangles we can say that \(a / c=b / d\); substituting this in the above equilibrium equation, we find \(\left(W_{1}\right)(c)=\left(W_{2}\right)(d)\). We may now consider as the significant quantities in the problem, the forces \(W_{1}\) and \(W_{2}\) and the distances \(c\) and \(d\), through which the weights have moved.

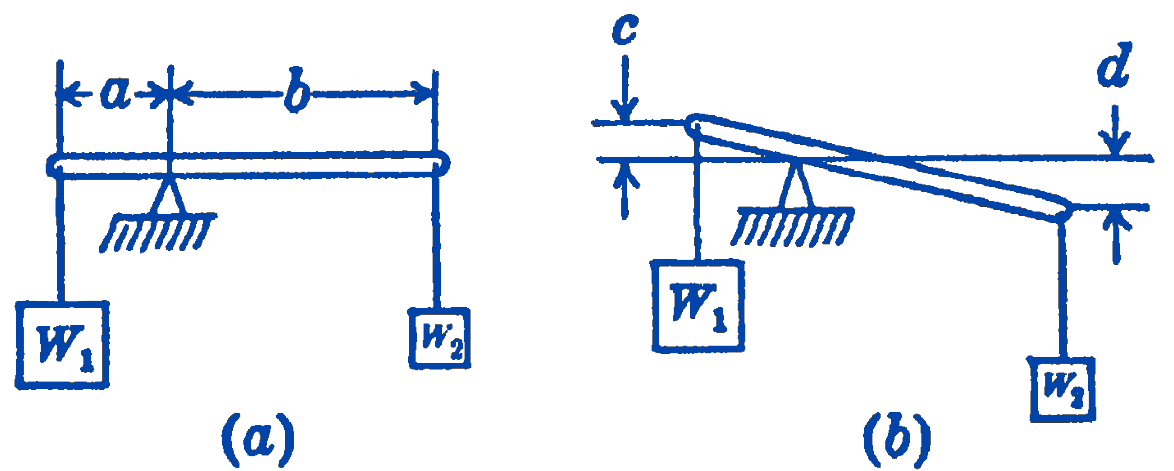
This second form of the equation is equivalent to the previous statement, so far as any practical solution of the problem is concerned. We have, however, approached the problem in a somewhat different way. In the first case we balance the moments of the system about the pivot point; in the second case we examine the work which is done by the forces of the system during some possible motion of the system. The universal applicability of this second point of view to the problems of mechanics was first indicated in 1717 by John Bernoulli, and this Principle of Virtual Displacements was taken as the foundation for the science of mechanics by Lagrange in his Mécanique Analytique.

Since the principle of virtual displacements introduces no new information into the science of mechanics, we cannot, by its use, solve problems which we would be unable to solve by the methods previously discussed. For certain types of problems, however, the principle leads directly to particularly simple results, and it is for this reason, and for the additional reason that the principle is the starting point for several important developments in dynamics, that we shall here consider the principle of virtual displacements.