In Fig. 1 are shown two vectors \(\mathbf{a}\) and \(\mathbf{b}\), which make an angle \(\theta < 180^\circ\) measured in the plane of the two vectors. The vector product \(\mathbf{a} \times \mathbf{b}\) is defined as a vector along line \(OB\) normal to the plane of the vectors \(\mathbf{a}\) and \(\mathbf{b}\), with such a direction that, if one looks in the direction \(OB\), a clockwise turn will bring the direction of \(\mathbf{a}\) into that of \(\mathbf{b}\). The rule for direction may also be stated by saying that the direction is that of the advance of a right-handed screw turned from \(\mathbf{a}\) to \(\mathbf{b}\). The magnitude of the vector product is defined as \((a)(b) \sin \theta\). The magnitude is thus equal to twice the area of the triangle shown shaded in Fig. 1. Because of the form in which it is written the vector product \(\mathbf{a} \times \mathbf{b}\) is often called the cross product.

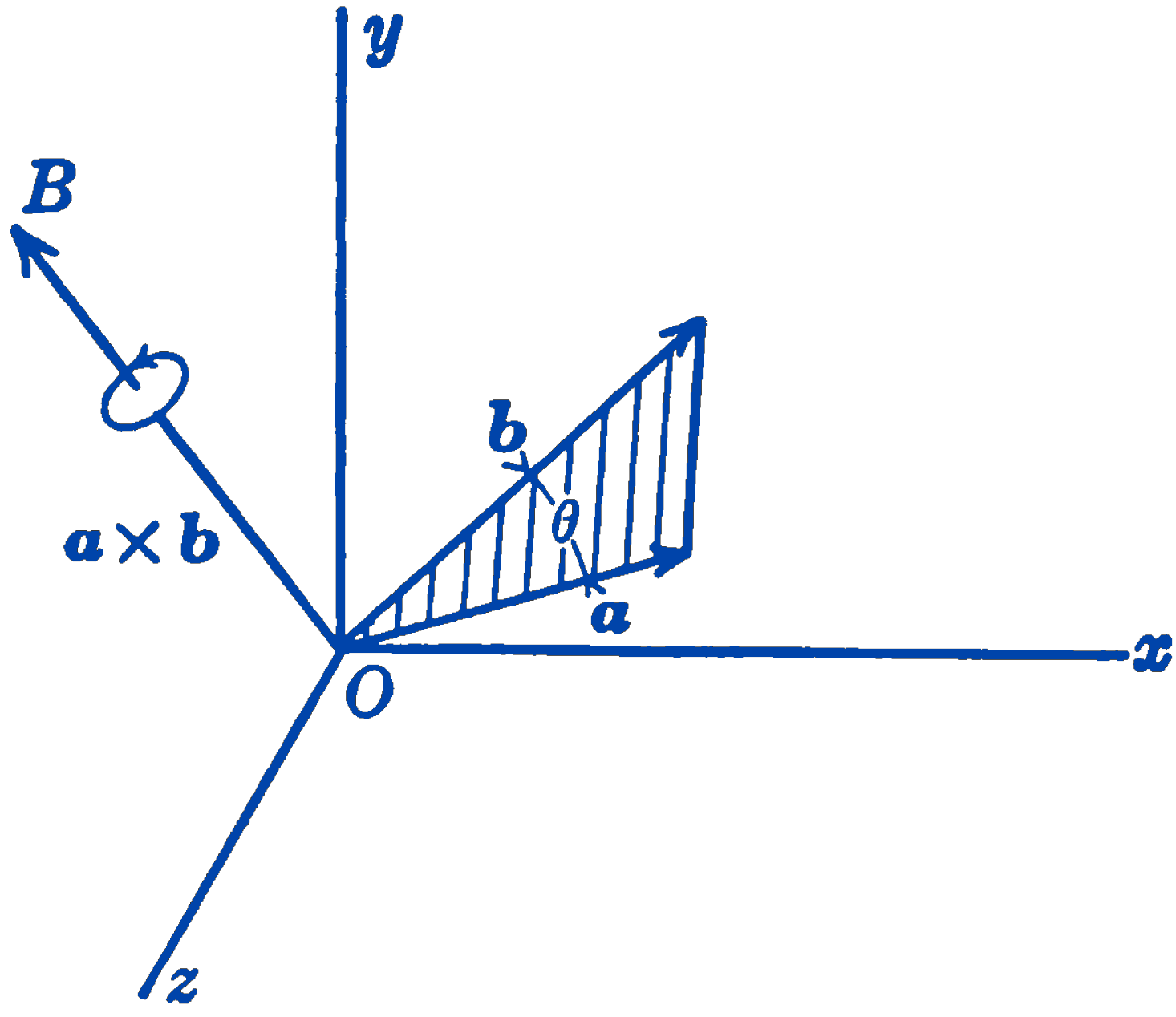
From the above definition it is seen that the vector product depends upon the order in which the vectors are taken. The vector product \(\mathbf{b} \times \mathbf{a}\) would have the same magnitude as \(\mathbf{a} \times \mathbf{b}\), but would have the opposite direction so that \[ \mathbf{b} \times \mathbf{a} = - \mathbf{a} \times \mathbf{b} \] i.e., vector products are not commutative.

Writing the vector product in the form of components, we have: \[ \begin{aligned} \mathbf{a} \times \mathbf{b} =& (a_x \mathbf{i} + a_y \mathbf{j} + a_z \mathbf{k}) \times (b_x \mathbf{i} + b_y \mathbf{j} + b_z \mathbf{k})\\ =& a_x b_z (\mathbf{i} \times \mathbf{i}) + a_x b_y (\mathbf{i} \times \mathbf{j}) + a_x b_z (\mathbf{i} \times \mathbf{k}) \\ &+ a_y b_x (\mathbf{j} \times \mathbf{i}) + a_y b_y (\mathbf{j} \times \mathbf{j}) + a_y b_z (\mathbf{j} \times \mathbf{k}) \\ &+ a_z b_x (\mathbf{k} \times \mathbf{i}) + a_z b_y (\mathbf{k} \times \mathbf{j}) + a_z b_z (\mathbf{k} \times \mathbf{k}) \end{aligned} \]

From the definition of the vector product, we have the following relations between the unit vectors \(\mathbf{i}, \mathbf{j}, \mathbf{k}\): \[ \mathbf{i} \times \mathbf{i} = \mathbf{j} \times \mathbf{j} = \mathbf{k} \times \mathbf{k} = 0 \] \[ \mathbf{i} \times \mathbf{j} = - \mathbf{j} \times \mathbf{i} = \mathbf{k} \] \[ \mathbf{i} \times \mathbf{k} = - \mathbf{k} \times \mathbf{i} = - \mathbf{j} \] \[ \mathbf{j} \times \mathbf{k} = - \mathbf{k} \times \mathbf{j} = \mathbf{i} \] hence: \[ \mathbf{a} \times \mathbf{b} = (a_y b_z - a_z b_y) \mathbf{i} + (a_z b_x - a_x b_z) \mathbf{j} + (a_x b_y - a_y b_x) \mathbf{k} \]