Given two vectors \(\mathbf{a}\) and \(\mathbf{b}\) at an angle \(\theta\) (Fig. 1)¹, the scalar product of the two vectors is defined as a scalar quantity having the magnitude \((a)(b) \cos \theta\). The scalar product is thus equal to the magnitude of one vector multiplied by the component of the second vector in the direction of the first vector. The scalar product is written \(\mathbf{a} \cdot \mathbf{b}\), with a dot between the two vectors, and hence it is often called the dot product.

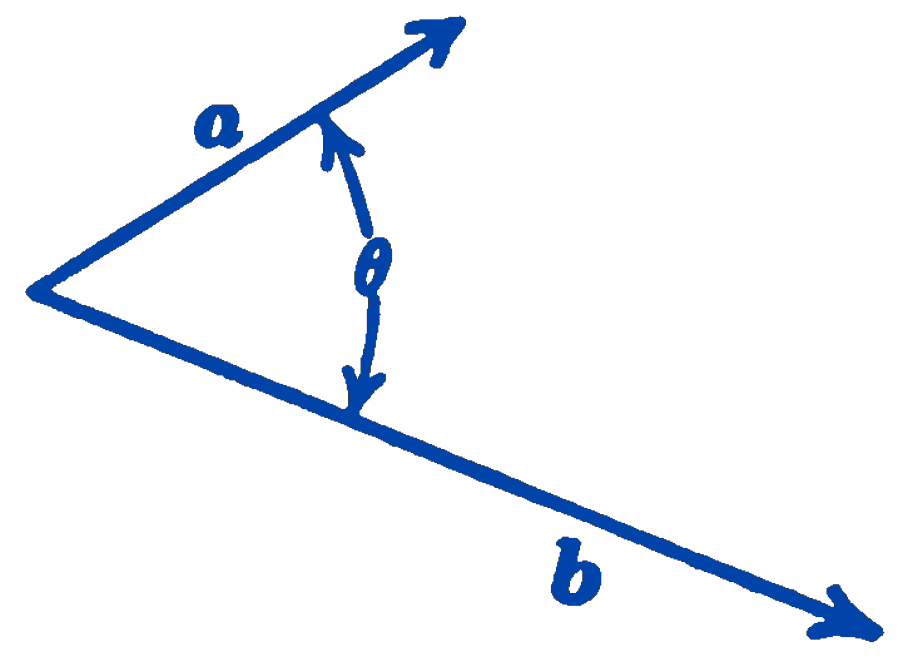
The same magnitude of the scalar product will result whether \(\mathbf{a}\) is multiplied by the component of \(\mathbf{b}\) in the direction of \(\mathbf{a}\), or \(\mathbf{b}\) is multiplied by the component of \(\mathbf{a}\) in the direction of \(\mathbf{b}\), since:

\[ (a)(b \cos \theta) = (b)(a \cos \theta) \]

so we may say:

\[ \mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a} \]

i.e., scalar multiplication is a commutative process.

If the angle between the two vectors is greater than \(90^\circ\), but less than \(270^\circ\), the scalar product will be negative.

The most common example of scalar products in mechanics is in connection with the work done by a force. If a force \(\mathbf{F}\) of constant magnitude has its point of application moved through some displacement \(\mathbf{S}\) then the work done by the force is defined as the scalar quantity which is equal to the displacement multiplied by the component of the force in the direction of the displacement, hence:

\[ \text{Work} = \mathbf{F} \cdot \mathbf{S} \]

We shall make use of the concept of work in later chapters.