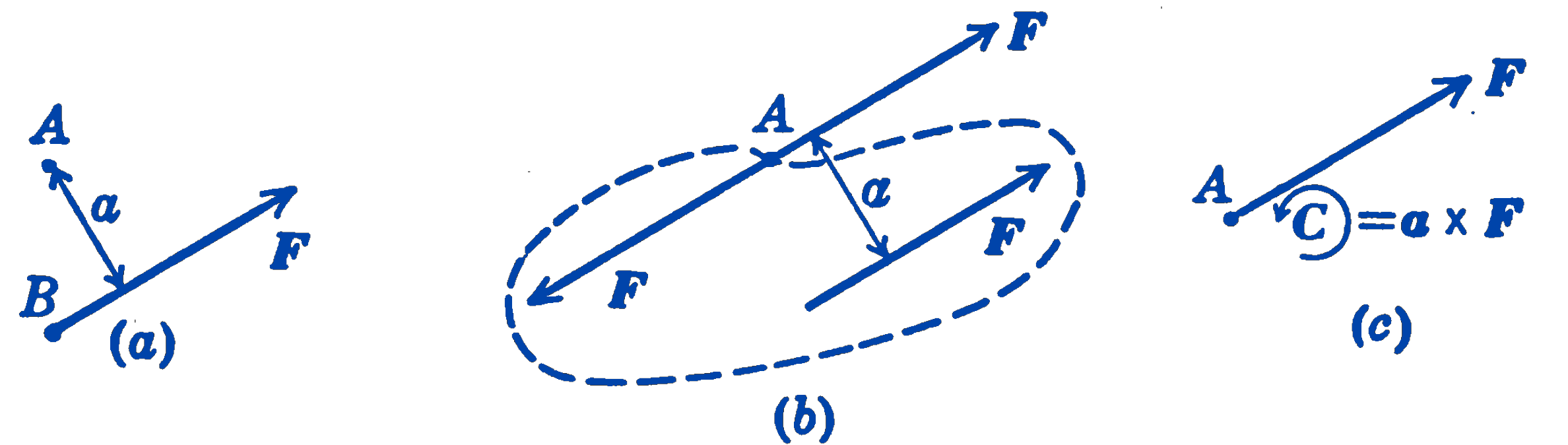
The action of a single force can always be duplicated by an equal parallel force plus a couple. Suppose that it is desired to resolve the force \(\mathbf{F}\) of Fig. 1a, whose point of action is \(B\), into a parallel force \(\mathbf{F}\) passing through the point \(A\), plus a couple. We introduce into the system the two equal and opposite forces \(\mathbf{F}\) and \(-\mathbf{F}\) acting at the point \(A\). Since these two forces form a system in equilibrium they can be added without altering the motional effects of the original \(\mathbf{F}\) upon the system. The circled forces in Fig. 1b can now be treated as a couple \(\mathbf{C} = \mathbf{a} \times \mathbf{F}\), and the original single force has been resolved into an equal parallel force and a couple.