The mutual influences between bodies, which are responsible for the motions of the bodies, are called forces. The idea of a force can be formed only with reference to the consequence of the action of the force upon a material body. The action of a force upon a body may be manifested in two different ways, as can be seen from the following example.

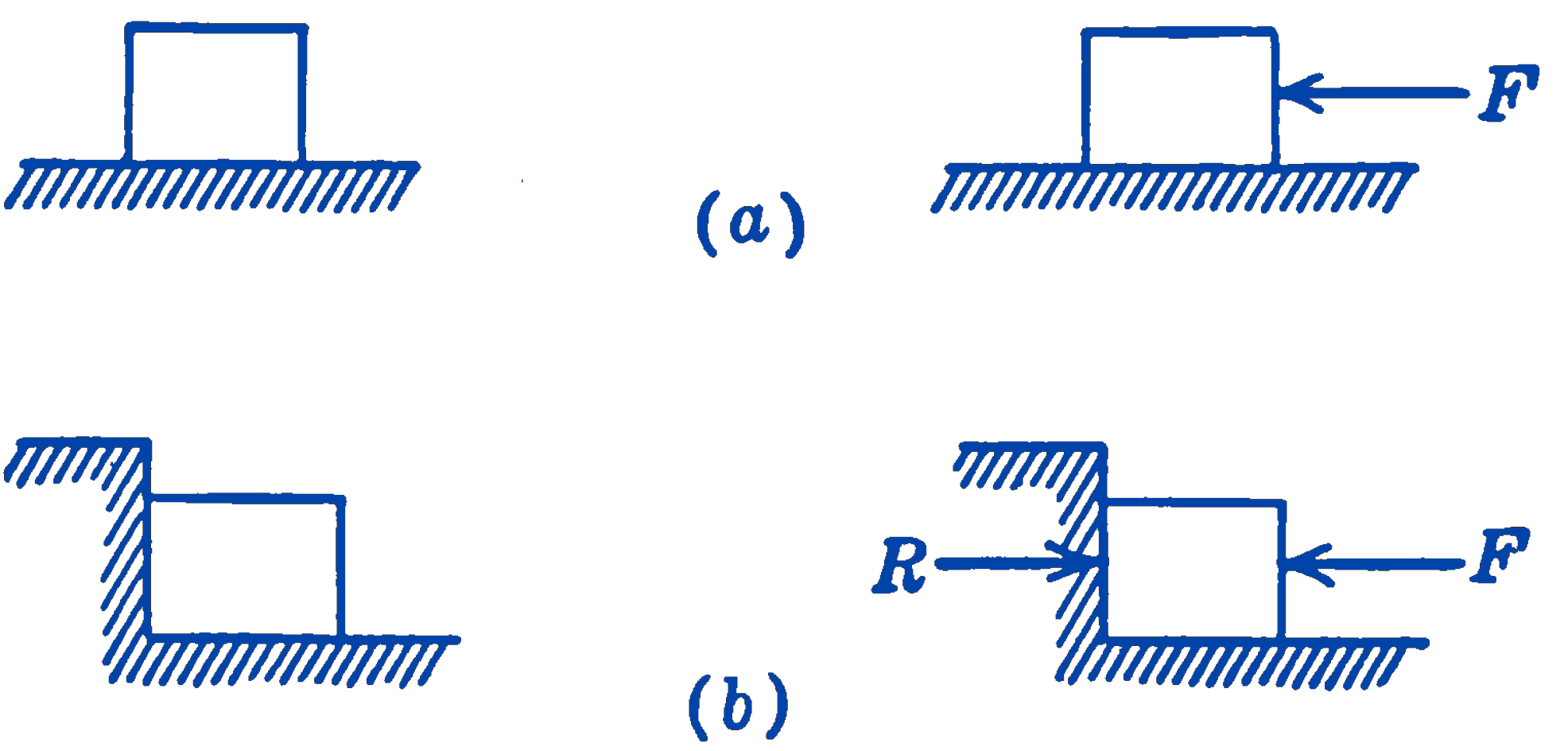
Consider the two situations illustrated in Fig. 1. A mass rests on a smooth horizontal plane. In (a) it is free to move either to the left or right whereas in (b) it is constrained so that it cannot move to the left. We now apply the force \(F\) as shown and note the results in each instance. In (a) the mass acquires an acceleration equal to the force divided by the mass, but in (b) the active force \(F\) is opposed by a reactive force \(R\), in such a way that \(R = -F\) and equilibrium of the system results. Thus in case (a) the effect of the force has been to change the motion of the mass, while in case (b) the effect of the force has been to set up a reactive force which maintains the system in equilibrium. The effect of the two forces \(R\) and \(F\) in case (b) on any actual body would be to cause a deformation of the body, in this case a compression. We may thus say that there are two effects of the action of a force on a material body—a motional effect and a deformational effect.

Either one of these effects could be used to define and to measure a force and in practice both are used. A common method of measuring the magnitude of a force is to measure the deformation which the force will set up in a calibrated spring balance. This method clearly makes use of the deformational effect of the force, since the system as a whole is in equilibrium.

It is also customary to define and to measure a force by means of its motional effects. The relation between the force exerted on a body and the motion which results is given by Newton’s Laws, which may be taken as a definition of a force. For our present purpose in statics, however, we need only emphasize that aspect of a force which we imply when we say “a force is a push or a pull,” and which is thus directly related to our muscular sense.

To specify completely the action of a force upon a body, the magnitude, direction, and point of application of the force must be given. A force may thus be represented by a vector which gives the magnitude and direction of the force and which indicates, by its location, the line of action and the point of application of the force.