When a number of forces act upon a body they form a force system. By the resultant force of a system we mean the vector sum of the forces of the system. To specify completely the motional effect of a system of forces, the line of action of the resultant force vector must also be known. The vector sum can be determined by any of the several methods for adding vector quantities. Analytical methods will be used for the most part in the present book, but graphical methods will be used when appropriate.

Consider a system of two forces in equilibrium. This situation can occur only if the two forces lie along the same straight line and are equal in magnitude and opposite in direction (Fig. 1a).

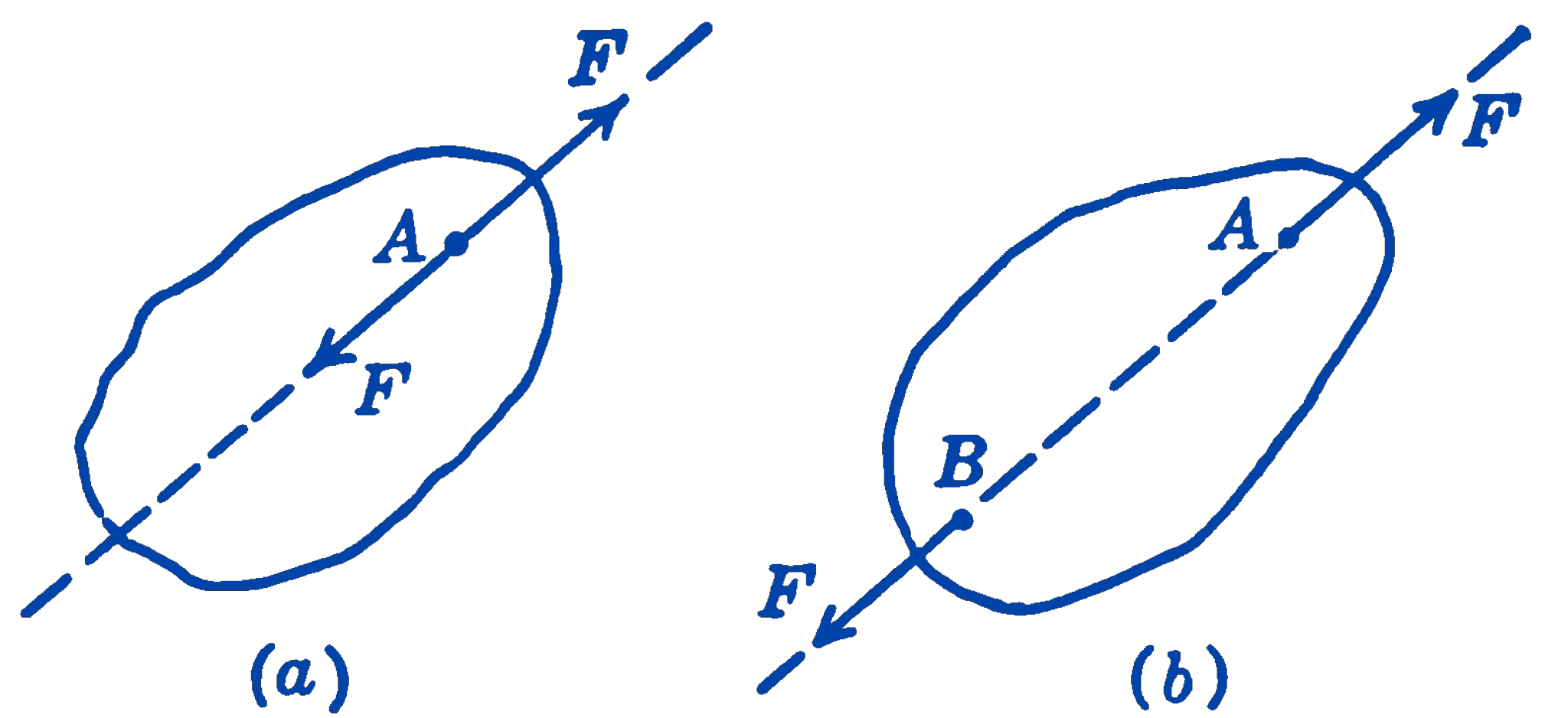
Suppose the system of Fig. 1a is changed so that the two forces which originally acted at the same point A now act at two different points, A and B, on the line of action of the two forces.

The system is still in equilibrium so far as the motion of the body is concerned, but the deformations of the system will have been altered. In general we mean by a force system in equilibrium, one whose resultant motional effect on a material body is zero. We thus conclude that the force \(F\) in Fig. 1b can be moved along its line of action from A to B without changing the conditions of equilibrium of the system. This conclusion can be given in the form of the principle of transmissibility, which states that a force can be considered to act at any point along its line of action, so far as the conditions of equilibrium are concerned.

A simplification often introduced into mechanics is the idea of a rigid body, defined as a body in which every particle maintains fixed distances from all of the other particles of the body. It follows that there can be no deformation of a rigid body, and only the motional effects of force systems which act upon a rigid body need to be considered. For rigid bodies, the principle of transmissibility is seen to be completely true, and in this sense the principle is more properly considered as a property of a rigid body than as a property of a force. The principles of statics, however, as they relate to systems in equilibrium and to the motional effects of forces, need not be restricted to rigid bodies. In fact, in many engineering problems in which the equations of equilibrium are used, it will be necessary to account for the deformations of the system in order to arrive at a complete solution.

In many problems it is desired to replace a single force by two or more forces which are equivalent to it. This problem occurs, for example, when a force may be exerted in a certain direction only, while it is desired to have a resultant force in some other direction. The two or more forces which replace the given force are called components of the force, and the process of finding the components is called the resolution of a force into components.