A couple has been defined as a system of two parallel forces equal in magnitude but opposite in direction. We shall now show that the sum of the moments of the forces of a couple is independent of the point about which the moments are taken.
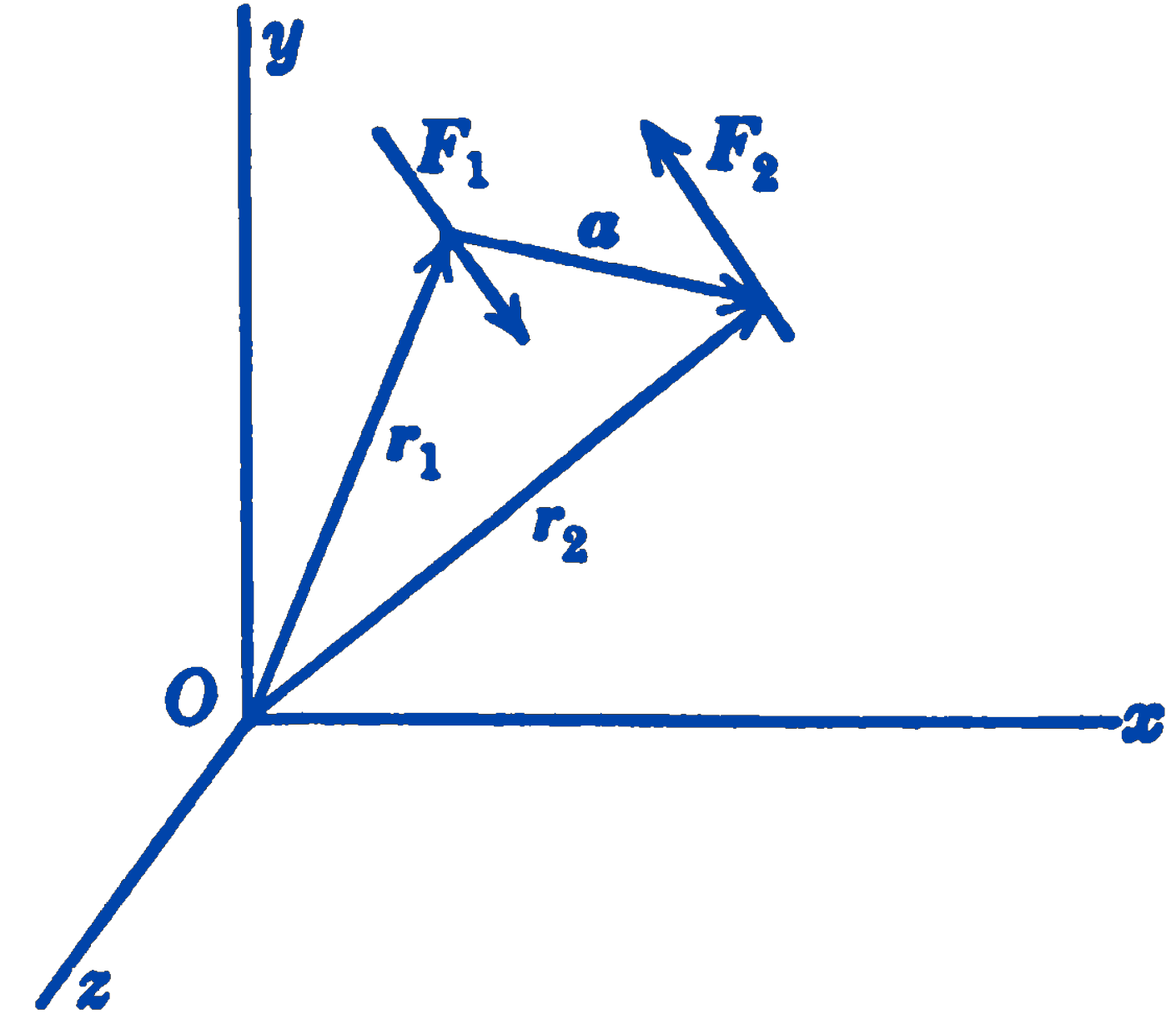
Consider two equal and opposite forces \(\mathbf{F_1}\) and \(\mathbf{F_2}\); \(\mathbf{F_1} + \mathbf{F_2} = 0\) (Fig. 1). Let \(\mathbf{r_1}\) and \(\mathbf{r_2}\) be vectors drawn from any point \(O\) to points on the lines of action of \(\mathbf{F_1}\) and \(\mathbf{F_2}\). \(\mathbf{a}\) is the vector \((\mathbf{r_2} - \mathbf{r_1})\). The sum of the moments of the two forces of the couple will be called the moment of the couple and will be represented by the vector \(\mathbf{C}\).
\[ \mathbf{C} = \mathbf{r_1} \times \mathbf{F_1} + \mathbf{r_2} \times \mathbf{F_2} \] Since \(\mathbf{F_1} = -\mathbf{F_2}\), this becomes:
\[ \mathbf{C} = (\mathbf{r_2} - \mathbf{r_1}) \times \mathbf{F_2} = \mathbf{a} \times \mathbf{F_2} \] Since \(O\) can be taken as any point without altering the vector \(\mathbf{a}\), the moment of the couple is independent of the center about which the moments are taken. The moment is thus a property of the couple itself and can be taken as a quantitative measure of the magnitude of the couple. A couple, therefore, is specified completely by the couple vector \(\mathbf{C} = \mathbf{a} \times \mathbf{F}\). The magnitude of the couple vector is equal to \((\mathbf{F})(\mathbf{a} \sin \theta) = (\mathbf{F})(d)\), where \(d\) is the perpendicular distance between the forces of the couple. The direction is normal to the plane containing the two forces and the sense corresponds to the direction of advance of a right-handed screw rotated by the forces of the couple.
Since \(\mathbf{C}\) is independent of any particular point, the couple vector does not have a unique line of action as does a force vector.
From the above definition of a couple as a vector, a number of characteristics follow directly:
- Two couples are equivalent (have the same motional effect upon a body) if their moments and directions are the same. The particular values of the force and the moment arm are not significant; it is only the product of the two which determines the action of the couple.
- The forces of a couple can be rotated through any angle in their plane, or translated to any position in the plane, without changing the motional effect of the couple upon a body.
- The forces of a couple can be translated into any parallel plane without changing the motional effect of the couple upon a body.
PROBLEMS
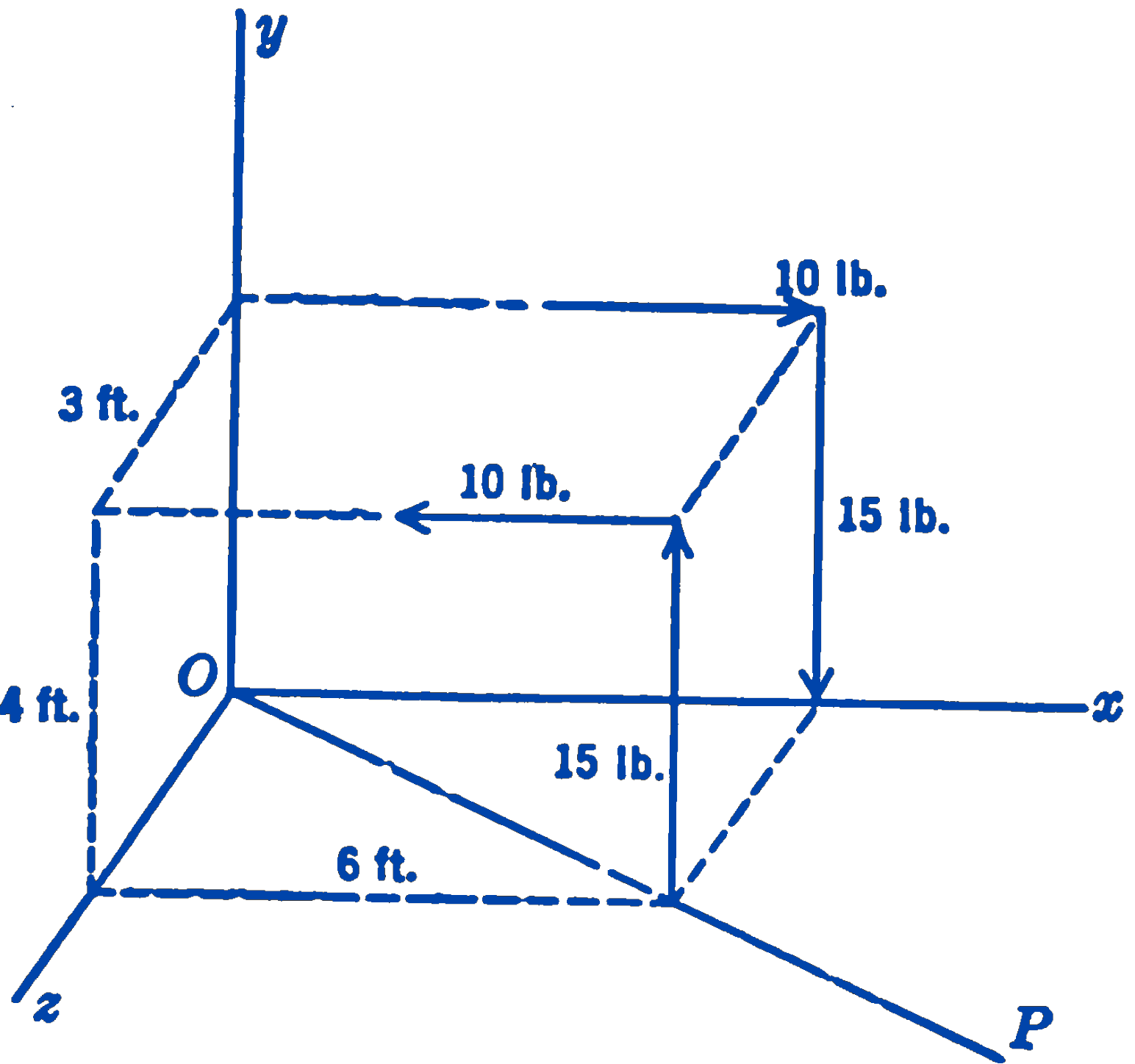
1. Given the two couples as shown in the diagram, find their sum:
(a) By adding the couple forces directly and thus forming a new couple.
(b) By adding the couple vectors.
answer
\(54.0\ \mathrm{ft}\cdot\mathrm{lb}\)
2. Referring to the diagram in the preceding problem, find the sum of the moments of the forces of the system about the line \(OP\) which lies in the \(xz\) plane. Do this by first taking moments directly about the line \(OP\), and then by finding the component of the resultant couple vector, as found in the preceding problem, along the line \(OP\).

answer
\(-40.1\ \mathrm{ft}\cdot\mathrm{lb}\)
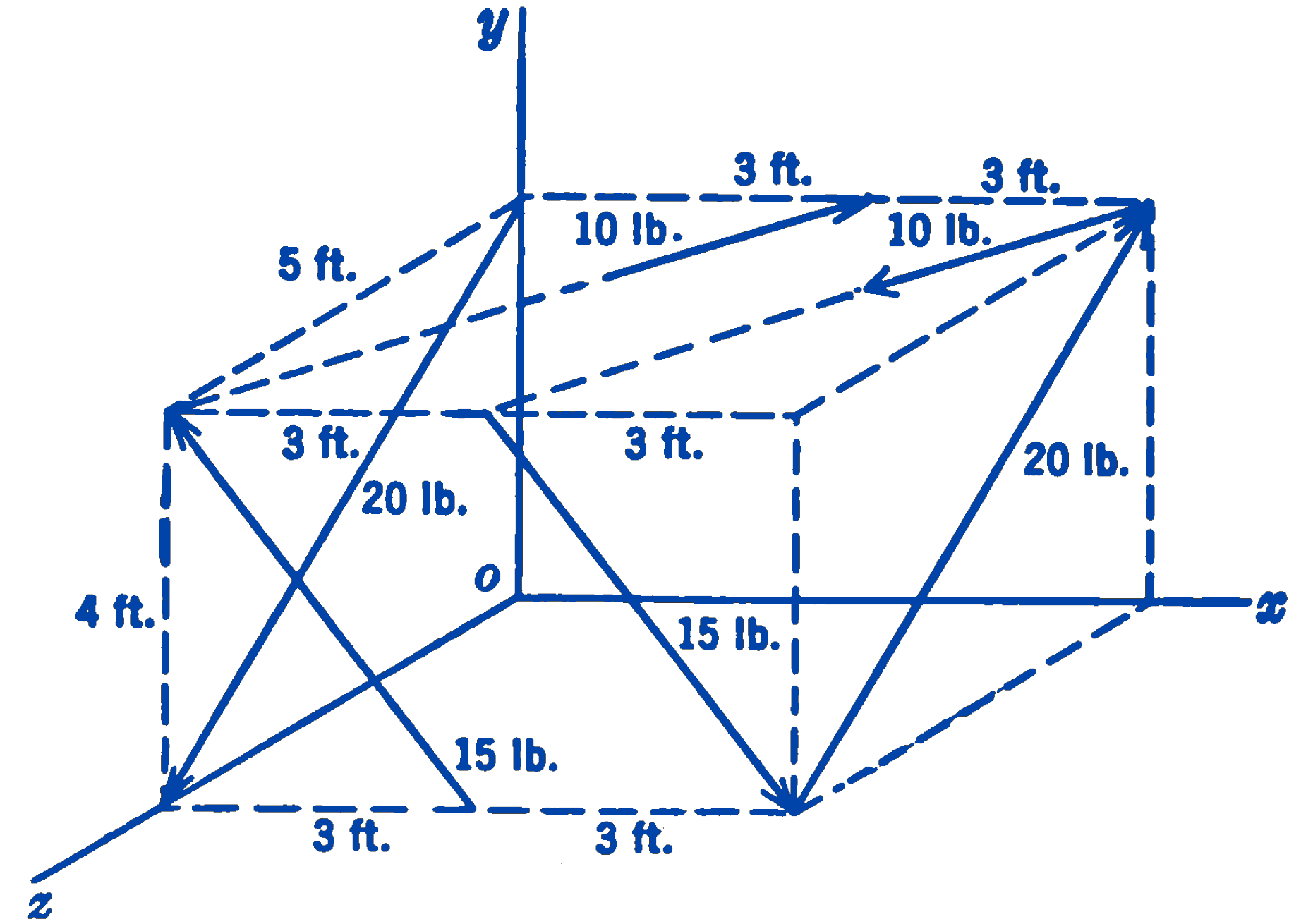
3. Find the resultant of the system of three couples shown in the diagram.
answer
\(68\mathbf{j} + 39\mathbf{k}\)
4. Find the resultant couple of the three space couples shown in the figure.
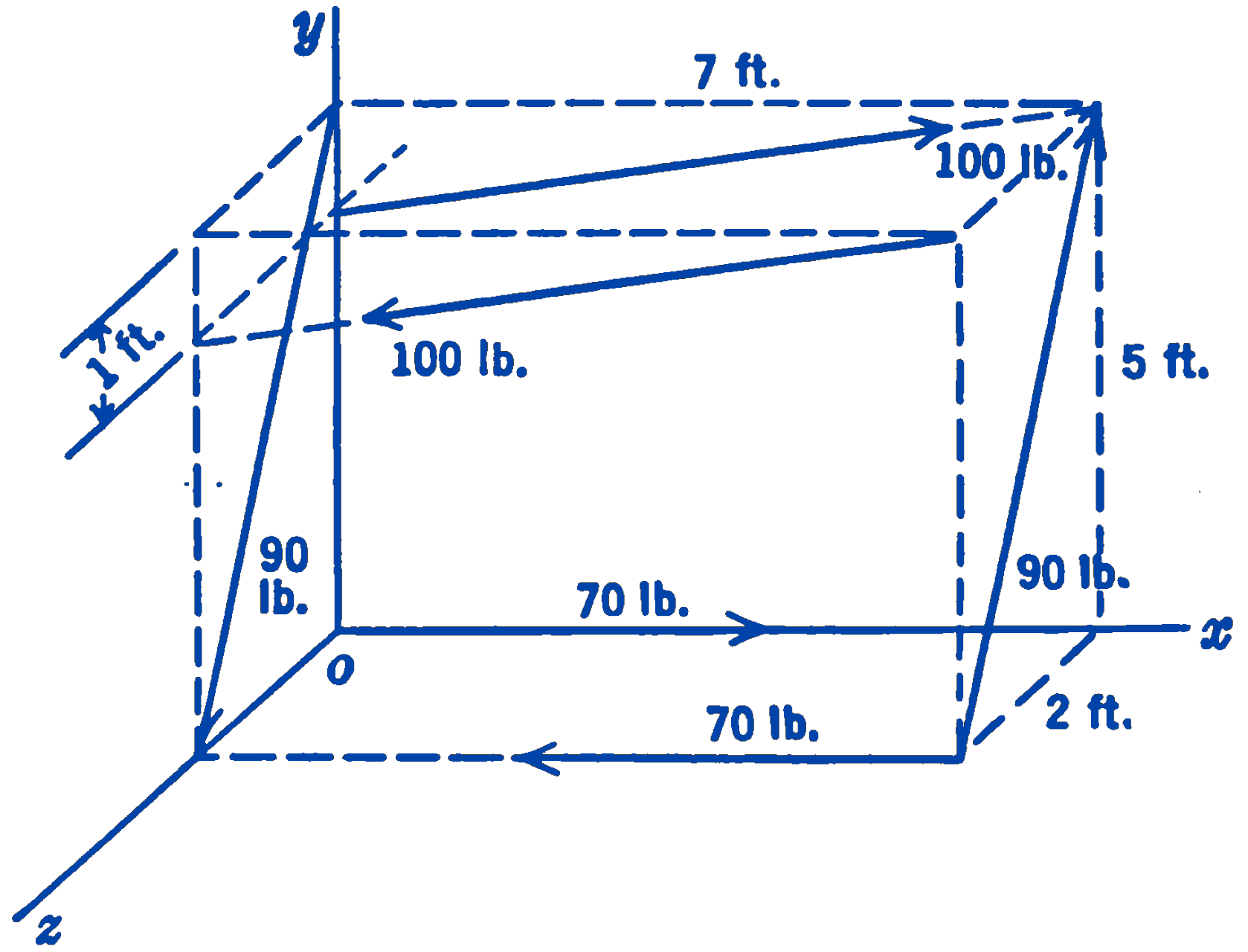
answer
\(28.3\mathbf{i} - 104\mathbf{j} - 585\mathbf{k}\)
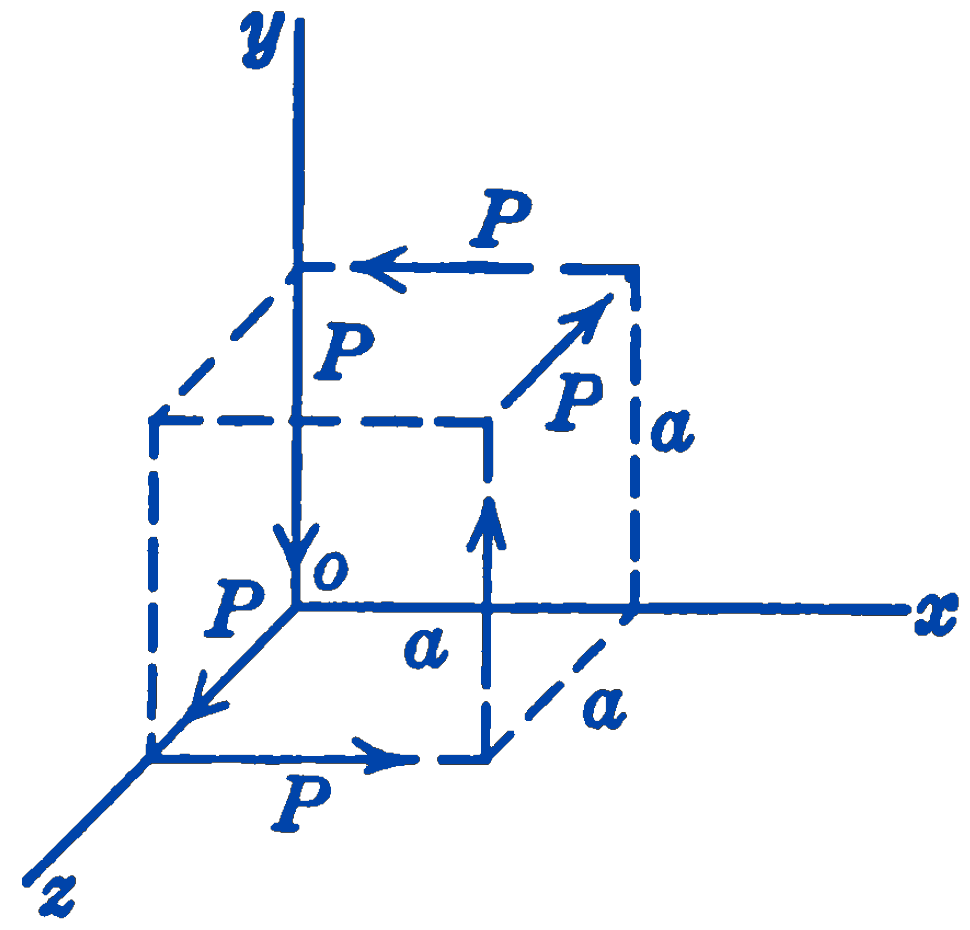
5. Six forces of equal magnitude act along the edges of a cube as shown in the diagram. Find the resultant of the system.