The description of a vector by means of its rectangular components is a convenient method, as we have already seen in the particular case of force vectors. The conventions with respect to a rectangular coordinate system may be seen in Fig. 1.

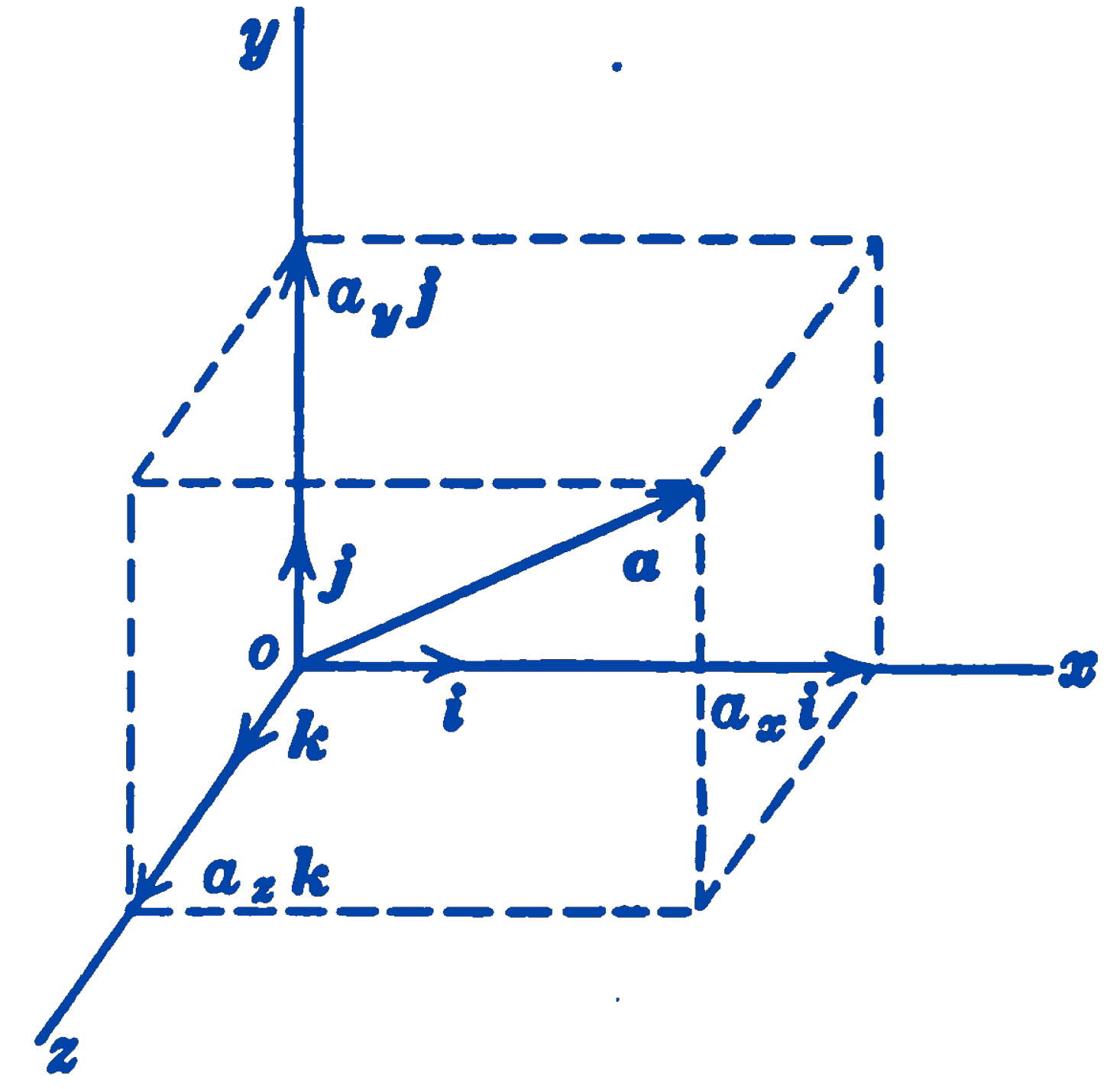
The unit vectors \(\mathbf{i}, \mathbf{j}, \mathbf{k}\) are defined as vectors having magnitudes of unity and the directions of the \(x, y, z\) coordinate axes respectively. The vector component along one of the coordinate axes can thus be indicated by giving the magnitude of the component with the proper unit vector. For example, in Fig. 1, the \(x\)-component of the vector \(\mathbf{a}\) would be written as \(a_x \mathbf{i}\) and the vector \(\mathbf{a}\) would be written as \(\mathbf{a} = a_x \mathbf{i} + a_y \mathbf{j} + a_z \mathbf{k}\).

We may write the scalar product of two vectors as follows:

\[ \mathbf{a} = a_x \mathbf{i} + a_y \mathbf{j} + a_z \mathbf{k} \] \[ \mathbf{b} = b_x \mathbf{i} + b_y \mathbf{j} + b_z \mathbf{k} \] \[ \begin{aligned} \mathbf{a} \cdot \mathbf{b} =& (a_x \mathbf{i} + a_y \mathbf{j} + a_z \mathbf{k}) \cdot (b_x \mathbf{i} + b_y \mathbf{j} + b_z \mathbf{k})\\ =& a_x b_x (\mathbf{i} \cdot \mathbf{i}) + a_x b_y (\mathbf{i} \cdot \mathbf{j}) + a_x b_z (\mathbf{i} \cdot \mathbf{k}) \\ &+ a_y b_x (\mathbf{j} \cdot \mathbf{i}) + a_y b_y (\mathbf{j} \cdot \mathbf{j}) + a_y b_z (\mathbf{j} \cdot \mathbf{k}) \\ &+ a_z b_x (\mathbf{k} \cdot \mathbf{i}) + a_z b_y (\mathbf{k} \cdot \mathbf{j}) + a_z b_z (\mathbf{k} \cdot \mathbf{k}) \end{aligned} \] From the definition of a scalar product, we have the following relations between the unit vectors: \[ \mathbf{i} \cdot \mathbf{i} = \mathbf{j} \cdot \mathbf{j} = \mathbf{k} \cdot \mathbf{k} = 1 \] since in each case the vectors have magnitudes of 1 and are in the same direction. Also: \[ \mathbf{i} \cdot \mathbf{j} = \mathbf{j} \cdot \mathbf{k} = \mathbf{k} \cdot \mathbf{i} = \mathbf{i} \cdot \mathbf{k} = \mathbf{j} \cdot \mathbf{i} = \mathbf{k} \cdot \mathbf{j} = 0 \] since the two vectors of the respective sets are perpendicular. The dot product is, therefore,

\[ \mathbf{a} \cdot \mathbf{b} = a_x b_x + a_y b_y + a_z b_z \]