Dry friction, of the kind discussed above, is most usually found in those machines in which the frictional force is a useful element, such as brakes and clutches, since in these cases it is desirable to have large coefficients of friction. In another large class of applications, however, it is desired to have as low a coefficient of friction as possible, since the friction is an undesirable element and represents a loss of power in the machine. For such applications one uses thick-film lubrication or a rolling action to reduce the frictional forces. The friction forces involved in these types of support are entirely different from the dry friction problem discussed above.

In thick-film lubrication the two contact surfaces are separated by a film of lubricant, such as oil, which is thick enough so that there is no metal-to-metal contact. In this case, the tangential forces necessary to cause motion are only those required to shear the layers of oil, and these frictional forces then depend upon the properties of the lubricating substance rather than on the material or the surface finish of the metals.

Consider two surfaces which are separated by a volume of fluid, as in Fig. 1. If we imagine that the oil film is maintained when the surfaces are stationary, then it will be seen that the coefficient of friction for such a situation would be zero, since a fluid at rest by definition is not able to support any tangential forces. In this event any small force \(F\) would suffice to set the upper body into motion. The coefficient of kinetic friction, however, is not zero, since it requires a definite force to shear a fluid at a given rate. The magnitude of this force is related to the velocity and the areas involved and also depends on the viscosity of the fluid, which we now proceed to define. Consider a horizontal layer of the fluid, of thickness \(d y\), as shown in Fig. 1. The lower surface of the layer moves with a velocity \(u\) and the upper surface moves with a velocity \(u+d u\). To maintain this steady flow requires a resultant force \(F\) on both surfaces, as shown in the free-body diagram. It was assumed by Newton that this drag force \(F\) was directly proportional to the surface area \(A\) of the layer, and the velocity gradient \(d u/ d y\) : \[ F=\mu A \frac{d u}{d y}. \] The validity of this assumption is checked by experiment, and it is found for a given fluid at a given temperature that \(\mu\) is a constant.

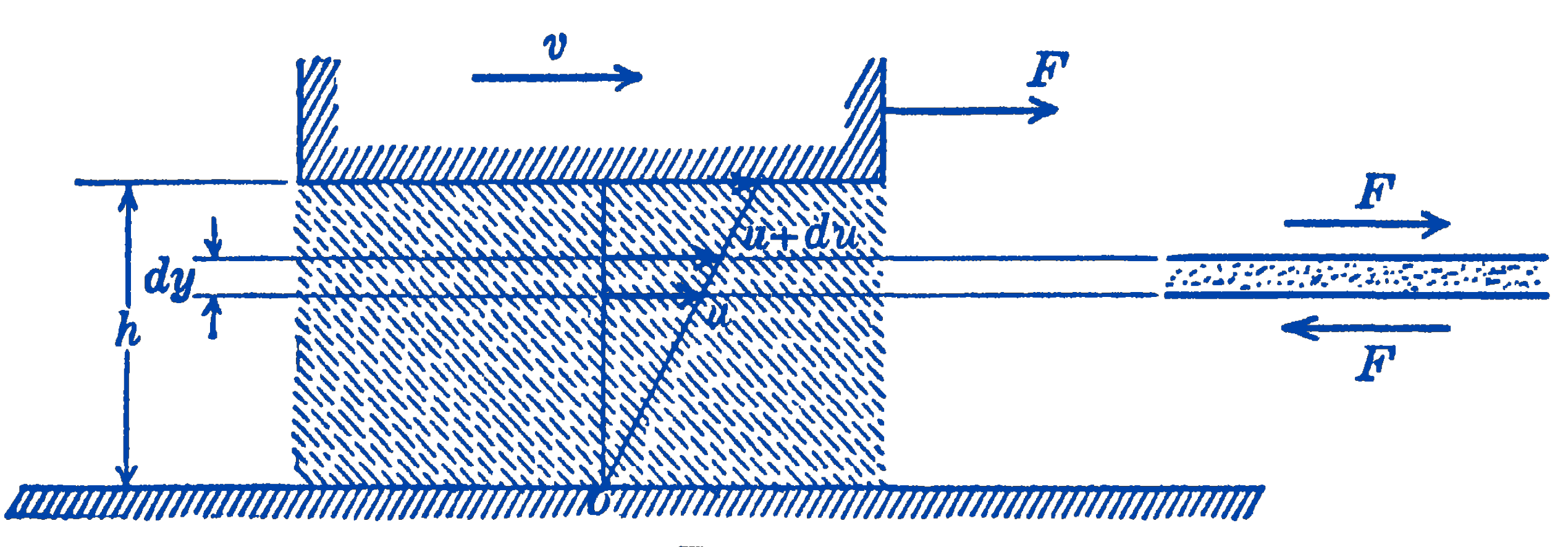
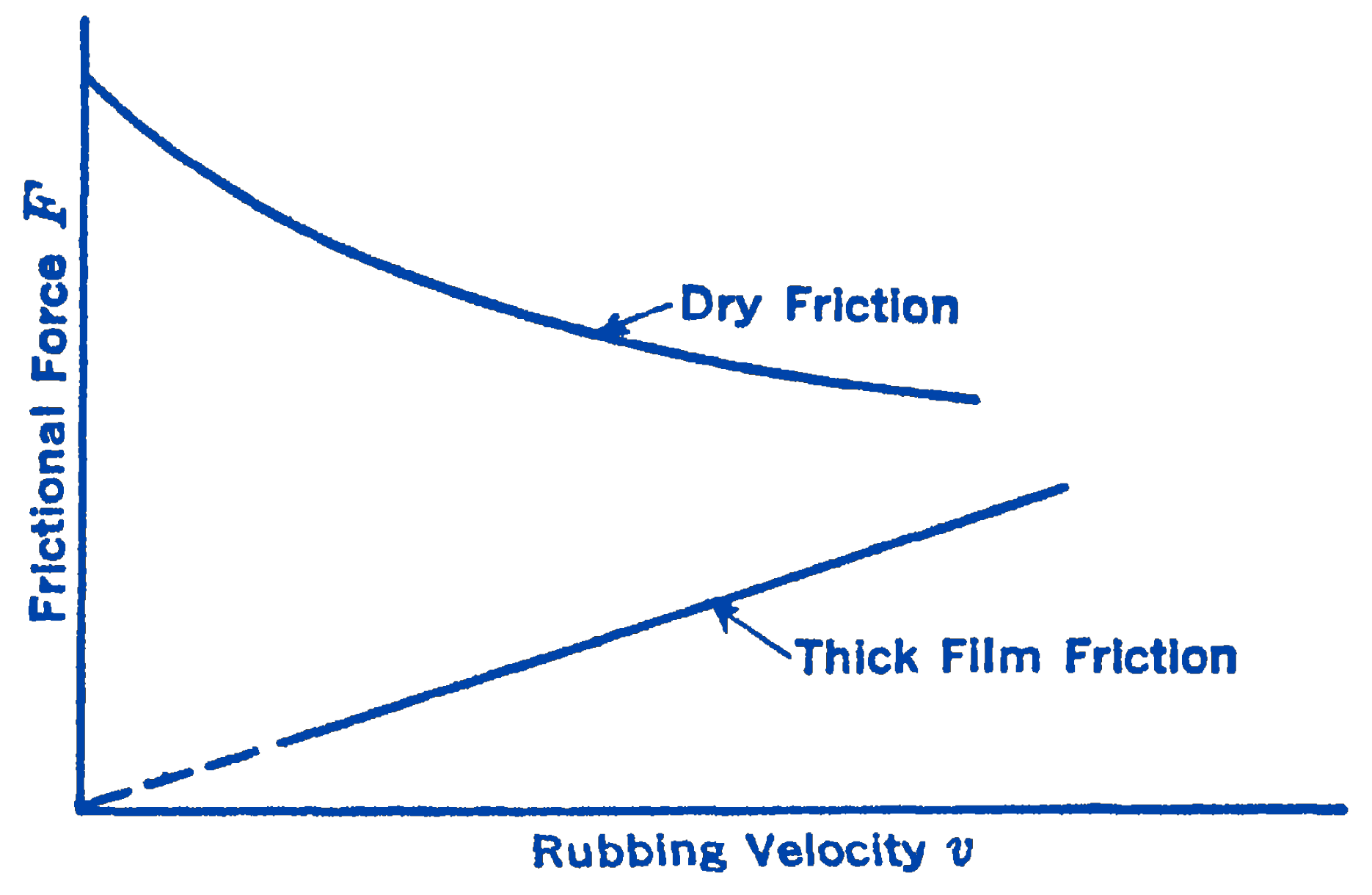
In Fig. 1 we may find the force \(F\) necessary to move the upper surface with a velocity \(v\) with respect to the lower surface, where \(h\) is the total fluid thickness. If we assume that the fluid elements directly adjacent to the moving surface have a velocity \(v\) while the fluid elements directly adjacent to the stationary surface are at rest, and that the velocity distribution across the fluid layer is linear, we have \[ \frac{d u}{d y}=\frac{v}{h} \] and \[ F=\frac{\mu A}{h} v. \] Thus, for thick-film lubrication the total frictional force is directly proportional to the velocity of the body. There is thus seen to be a great difference between thick-film friction and dry friction, for which the frictional force decreases with velocity (Fig. 2).

One of the most common applications of thick-film lubrication is to cylindrical bearings. In Fig. 3 a shaft of diameter \(d\) rotates at \(n\) revolutions per minute in a stationary bearing. The thickness of the lubricant between the shaft and the stationary housing is, of course, greatly exaggerated in the diagram. A load \(P\) acts upon the shaft. We assume that the bearing is centered in the shaft so that the film of oil is of constant thickness \(c\), and that the velocity varies linearly across the film. Then, if \(F\) is the friction force, and \(l\) is the length of the bearing: \[ F=\mu \pi d\, l \frac{v}{c}=\mu \pi d\, l \frac{n \pi d}{c} \]

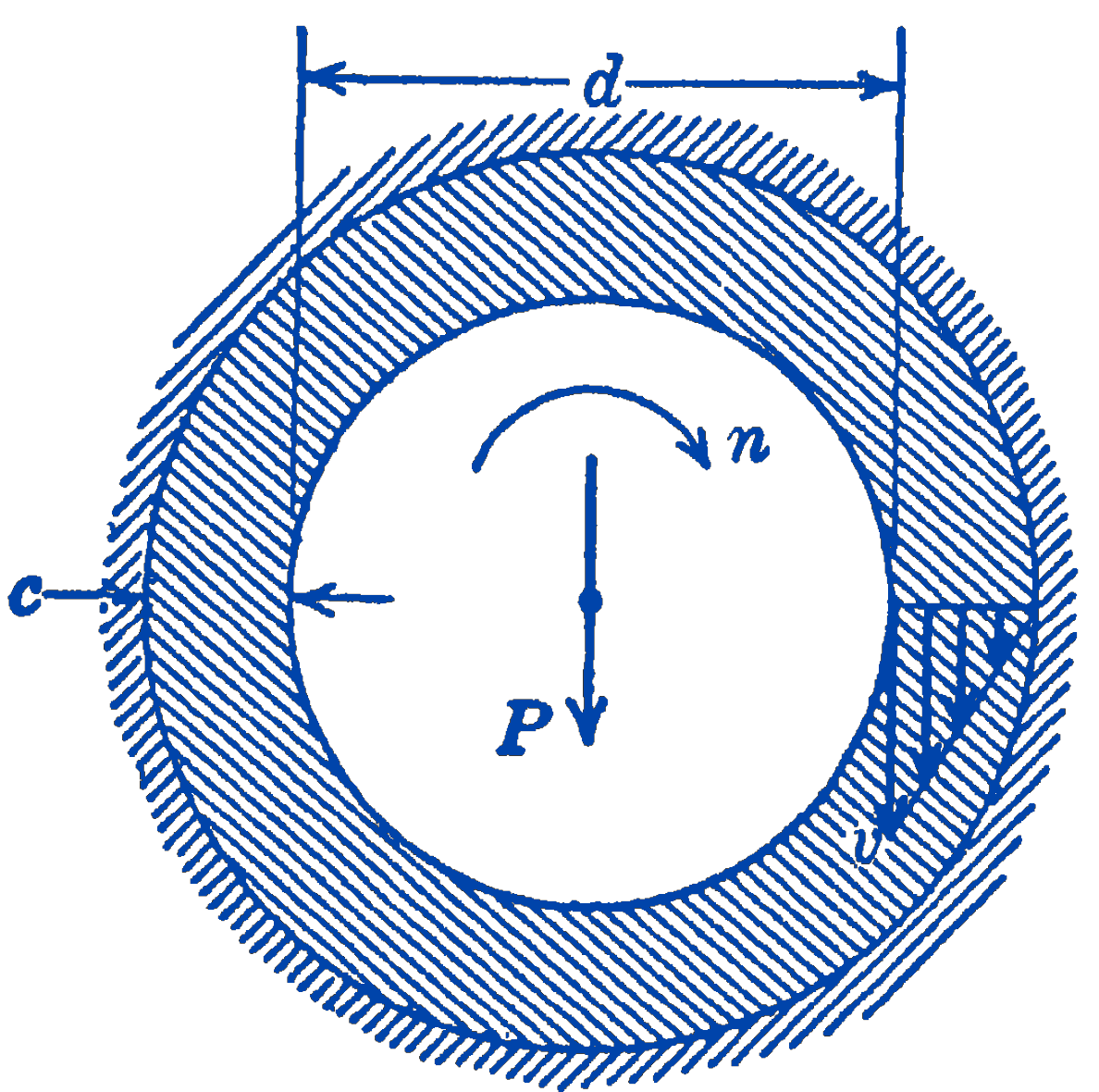
If we define the bearing pressure as the load divided by the projected area of the bearing: \[ p=\frac{P}{d\, l} \] we have: \[ F=\mu \pi \frac{P}{p} \frac{n \pi d}{c} \] The “coefficient of friction” of the bearing can be defined as the total friction force divided by the load \[ \frac{F}{P}=\pi^{2}\left(\frac{\mu n}{p}\right)\left(\frac{d}{c}\right) \] This equation thus relates all of the significant quantities involved in the design of such a bearing.

In an actual bearing, the assumption of an oil film of uniform thickness would not be true. The complete solution of the problem for a non-uniform oil film is a problem in hydrodynamics which is taken up in connection with the theory of journal bearings. The foregoing equation is accurate enough, however, to give a useful first approximation to bearing performance, and it is often used in preliminary design.

There is a third type of friction which is frequently encountered. In many cases it is not possible to maintain a perfect oil film so that there does occur a certain amount of contact between surfaces, or so that the oil film is so thin that the amount of frictional force is affected by attractive forces set up between the surfaces. This so-called boundary lubrication will thus depend not only on the lubricant properties, but also upon the surface finishes and materials. There is the additional complication that very thin films of lubricants possess special properties, and such phenomena as an adsorption of the lubricant on the metal surfaces occur. The behavior of this boundary friction is somewhere between that of dry friction and that of thick-film friction. Because of the many factors involved, the coefficients of friction for this case must be obtained experimentally under the exact operating conditions.