A commonly used machine element in which friction plays an important part is the screw thread. Such devices are used for various fastenings, for transferring motion, and for exerting large forces. We will consider a screw-jack, as shown in Fig. 1a.

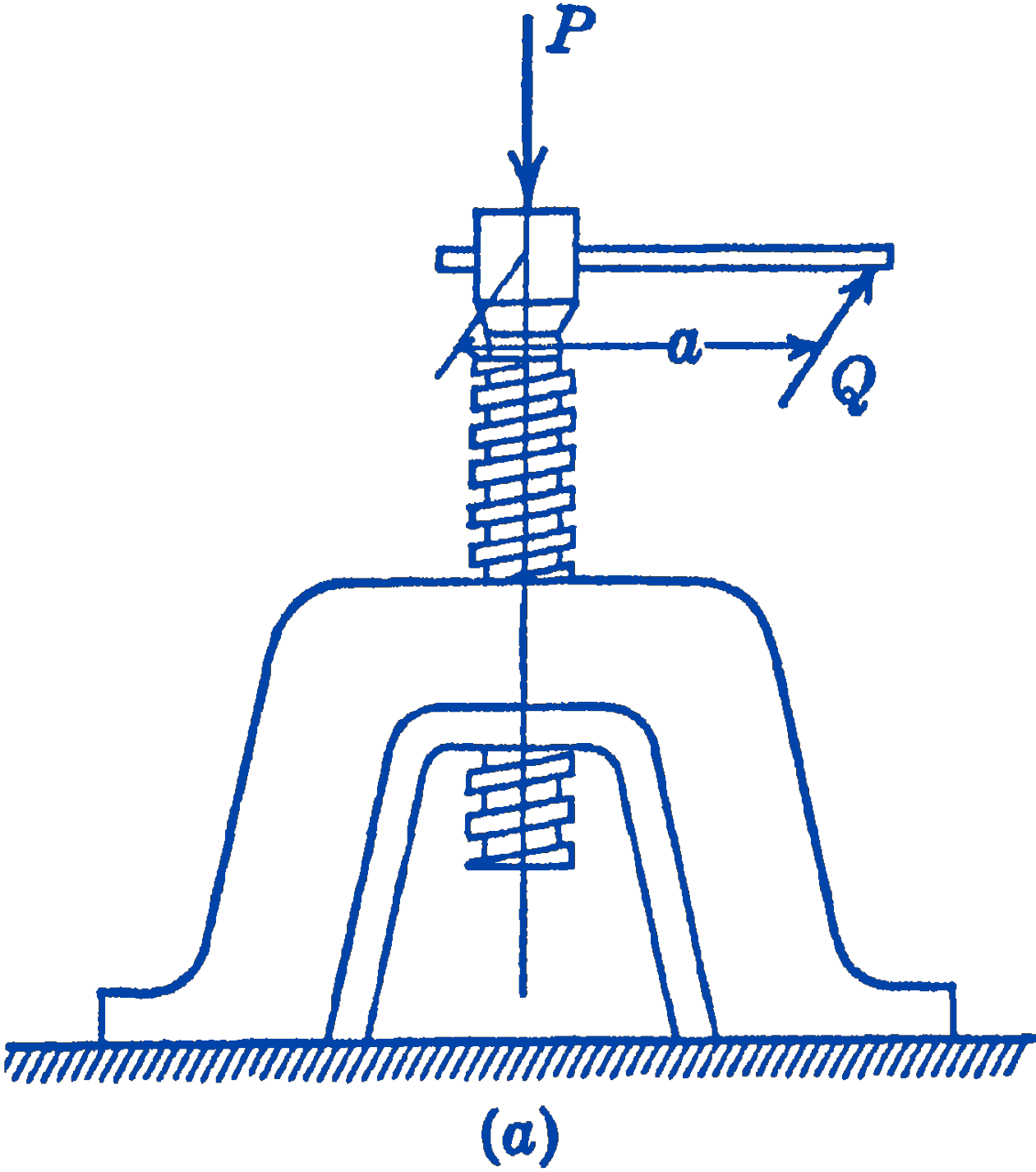
We first consider the case in which the axial load \(P\) is raised by means of the applied moment \(M=Q a\). In Fig. 1b, the forces acting on the screw thread are shown. In reality, these forces exerted on the screw thread by the nut are distributed all around the thread and usually over several threads. We show in the diagram only the forces acting on one typical element of the nut. We also limit our treatment to a square thread; thus the forces all lie in planes parallel to the axis of the screw. In Fig. 1c, the fact that a screw thread is simply an inclined plane wrapped around a cylinder may be seen. The mean radius of the thread, at which the forces are assumed to act, is \(r\) and the distance the thread advances in one revolution-the pitch of the screw-is \(p\).

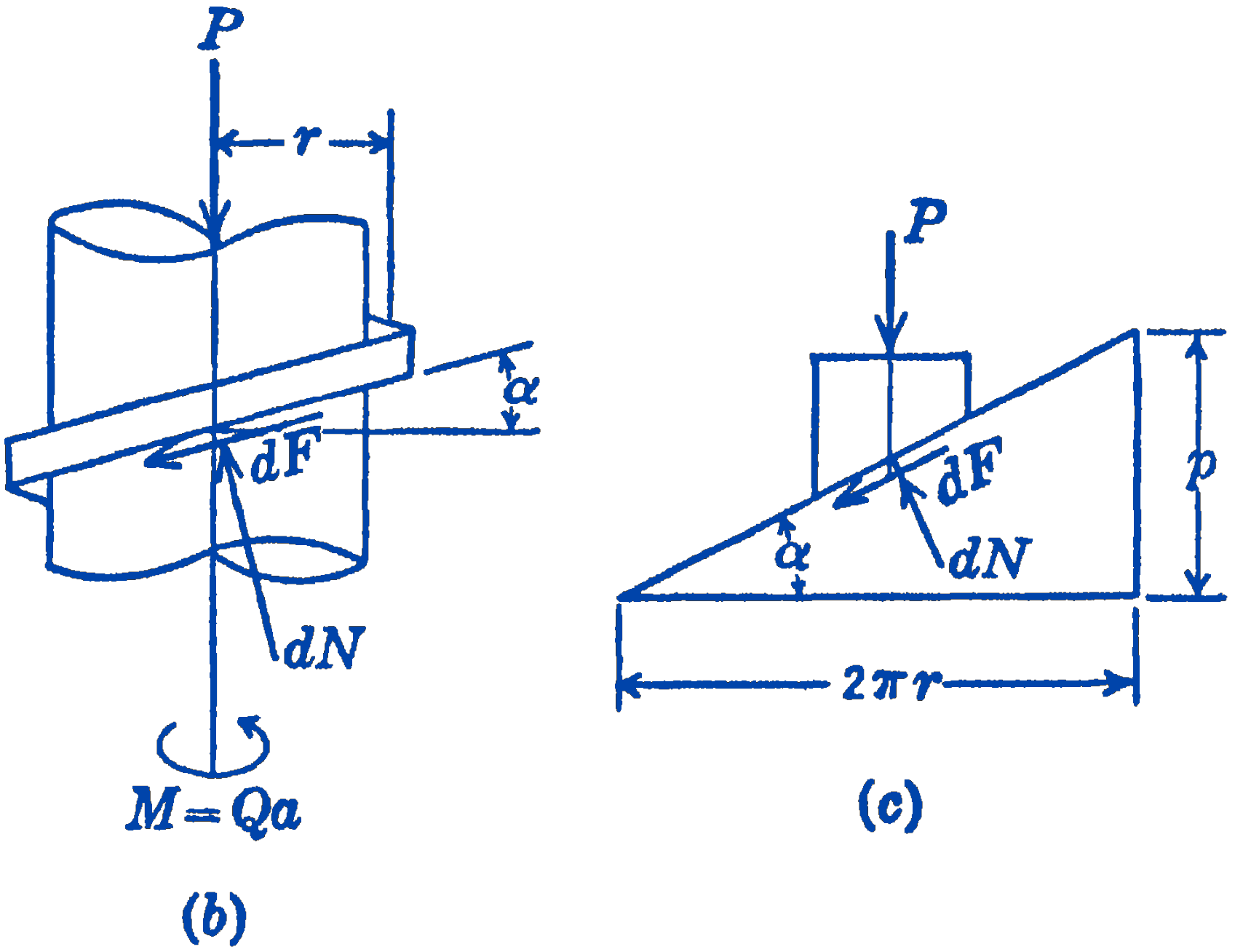
Then from the free-body diagram of Fig. 1b: \[ \begin{aligned} \sum F_{y} & =0=-P+\sum(-d F \sin \alpha+d N \cos \alpha) \\ \sum M & =0=M-r \sum(d F \cos \alpha+d N \sin \alpha) \\ M & =r \sum(d F \cos \alpha+d N \sin \alpha) \\ & =r(\mu \cos \alpha+\sin \alpha) \sum d N \\ P & =(\cos \alpha-\mu \sin \alpha) \sum d N \\ M & =Pr \frac{(\mu \cos \alpha+\sin \alpha)}{(\cos \alpha-\mu \sin \alpha)} \end{aligned} \] Dividing through by \(\cos \alpha\) and putting \(\mu=\tan \phi\), this becomes \[ M=\operatorname{Pr}\left(\frac{\tan \phi+\tan \alpha}{1-\tan \phi \tan \alpha}\right)=\operatorname{Pr} \tan (\phi+\alpha) \] If the load \(P\) is to be lowered instead of raised, the direction of the friction force changes, and the expression for the moment becomes \[ M=Pr \tan (\phi-\alpha) \] It is desirable to design a screw-jack so that it will be self-locking. By this we mean that, if we are raising a load and then stop applying the force, we do not want to have to hold the lever, i.e., to apply a moment, to prevent the load from lowering. The condition for self-locking, therefore, is that the moment required to lower the load must remain positive. From the foregoing formula for the moment required to lower the load, it will be seen that if the pitch angle \(\alpha\) is less than the friction angle \(\phi\) the screw will be self-locking.

A screw which is not self-locking is said to be an “overhauling” screw. An overhauling screw and nut system can be driven in either direction; i.e., if the nut is translated, the screw will rotate.

If a screw is to be used as a driving element, the power lost in the machine because of friction may become a relatively large figure, and the efficiency of the screw becomes of significance.

The efficiency of a machine is defined as the ratio of the output to the input. For the problem of the screw-jack discussed above, the input can be computed from the torque required to raise the load, and the output from the magnitude of the load raised. If we suppose that the screw is being rotated at \(\omega\ \mathrm{rad} / \mathrm{s}\), then the power input is equal to \(M \omega\ \mathrm{ft}\cdot\mathrm{lb} / \mathrm{s}\), if \(M\) is the applied moment in \(\mathrm{ft}\cdot\mathrm{lb}\). The velocity with which the load is raised, if the screw is rotated at \(\omega\ \mathrm{rad} / \mathrm{s}\) is (see Fig. 1c): \[ \begin{gathered} v=\frac{p\ \mathrm{ft} / \mathrm{rev}}{2 \pi\ \mathrm{rad} / \mathrm{rev}} \cdot \omega \frac{\mathrm{rad}}{\mathrm{s}}=\frac{p \omega}{2 \pi} \frac{\mathrm{ft}}{\mathrm{s}} \\ v=r \omega \tan \alpha \end{gathered} \] hence the power output is: \[P r\omega \tan \alpha\] and \[ \begin{aligned} \text { efficiency } & =\frac{\text { output }}{\text { input }}=\frac{Pr \omega \tan \alpha}{Pr \omega \tan (\alpha+\phi)} \\ & =\frac{\tan \alpha}{\tan (\alpha+\phi)} \end{aligned} \] This same conclusion can be reached from a different viewpoint by noting that the efficiency can also be defined as the ratio of the torque which would be required to raise the load if there were no friction to the torque which is actually required.

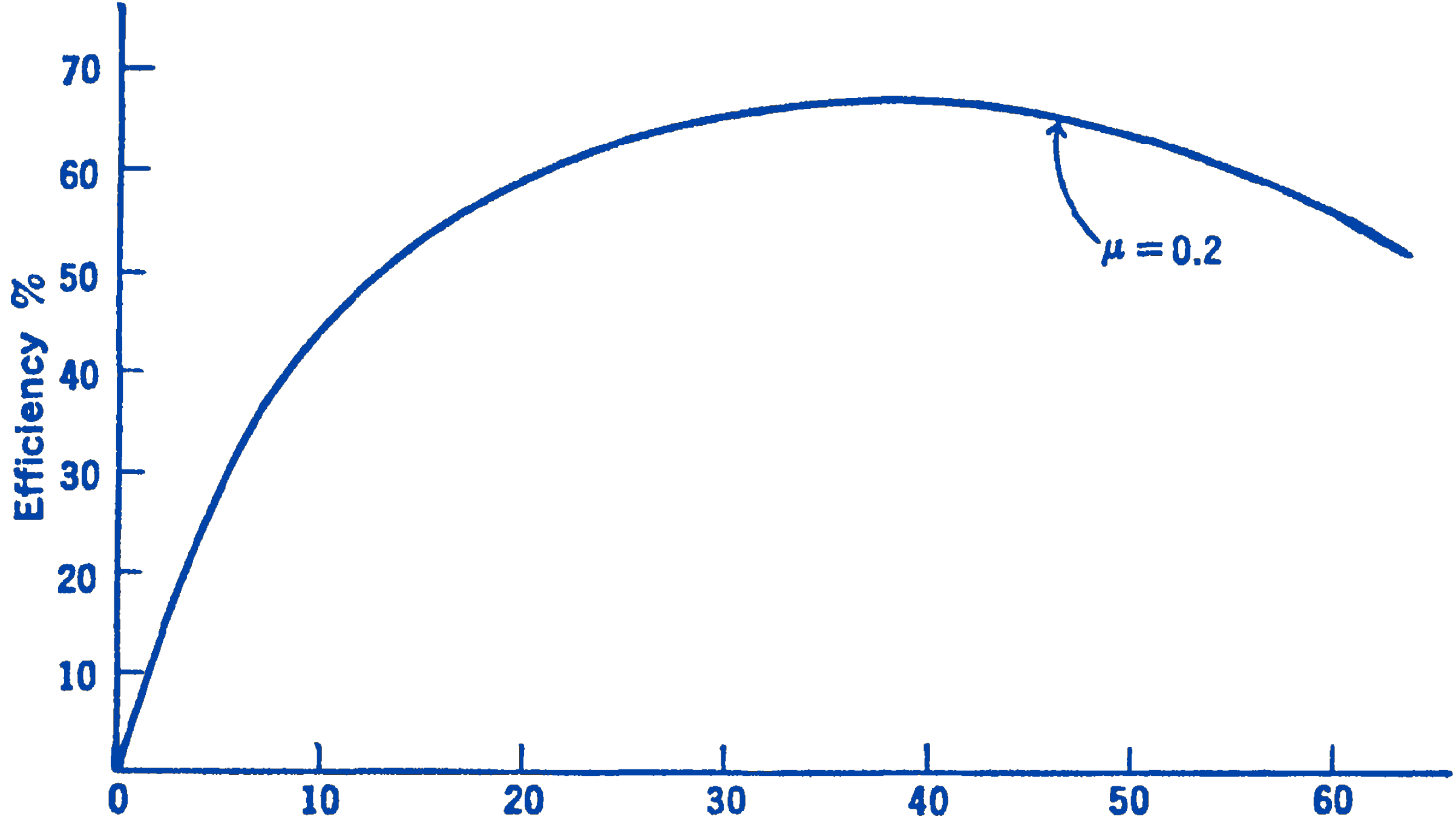
If we plot the efficiency of the screw versus the pitch angle \(\alpha\), we find that the curve has a definite maximum point, as may be seen in Fig. 2.

5.6.1 PROBLEMS