When two bodies roll together, for example when a wheel rolls on a rail or a roller in a bearing rolls against its race, a somewhat different type of frictional force is set up.
Imagine a wheel loaded by a force \(W\) moving to the left along a track with a uniform velocity, as in Fig. 1. Because of the continuous deformation of the track, a horizontal force \(F\) is required to keep the system in equilibrium, and this force is thus a measure of the rolling resistance of the wheel. The amount of rolling resistance is usually specified by giving the distance \(a\), which is sometimes called the coefficient of rolling resistance. It should be noted, however, that this distance a should not properly be called a coefficient, and that it is related to the frictional force as follows: \[ \begin{aligned} F & =N \sin \phi \\ W & =N \cos \phi \\ F & =W \tan \phi \end{aligned} \]
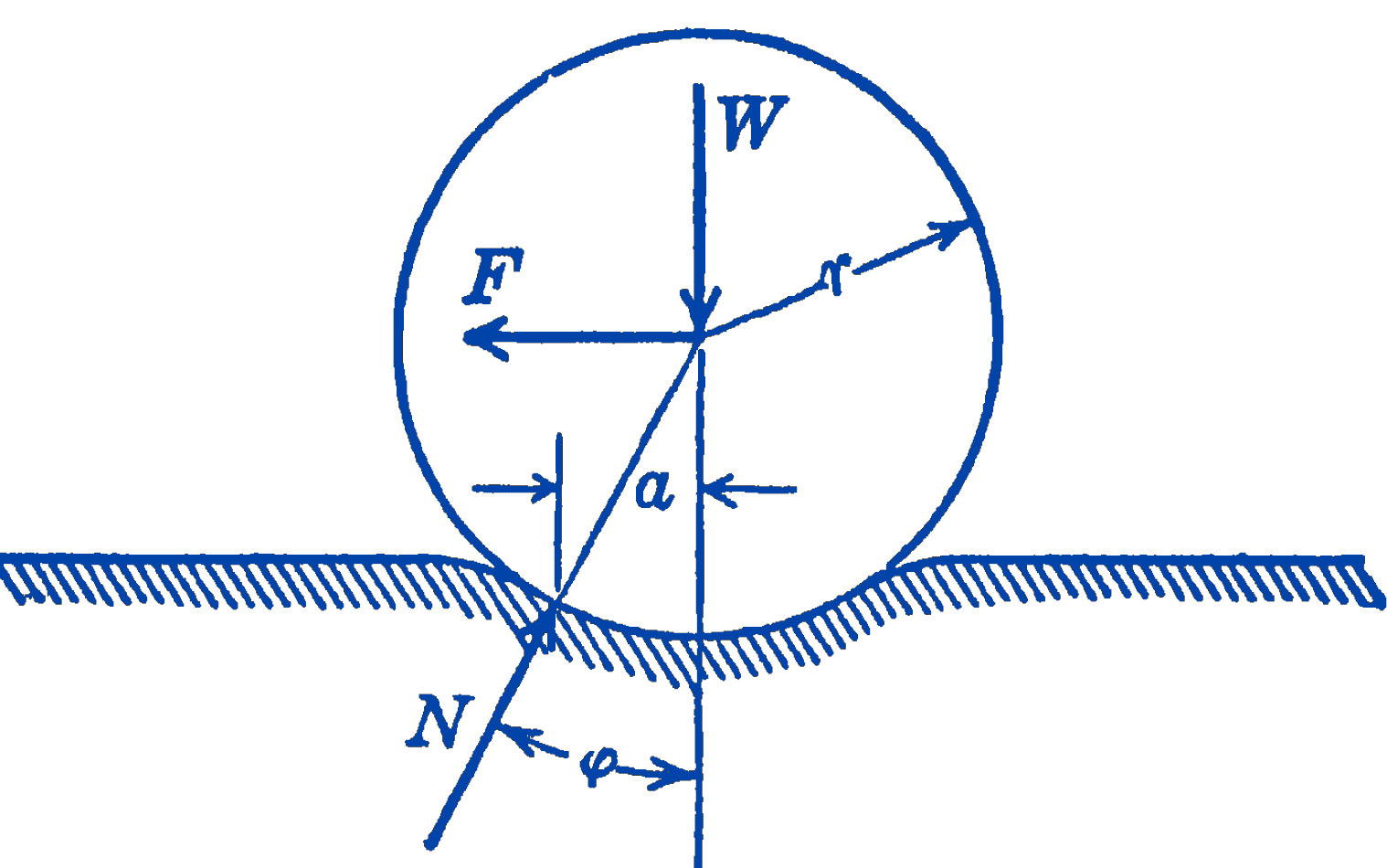
For small values of \(a\), \[\tan \phi \approx \dfrac{a}{r}\]so: \[ \bbox [5px,border:1px #f2f2f2;background-color:#f2f2f2]{F=\frac{W a}{r}} \] Some representative values of \(a\) are given in the following table:
| Materials | \(a\) (inches) |
|---|---|
| Hardened steel on hardened steel, clean smooth surfaces | 0.0002–0.0005 |
| Steel on steel | 0.002 |
| Hard wood on hard wood | 0.02 |
| Pneumatic rubber tires on smooth road | 0.02–0.03 |
It will be seen that rolling resistances are in general very much smaller than sliding resistance. This fact is made use of in many types of so-called “anti-friction” ball and roller bearings. While the coefficients of such bearings are very much less than the coefficient of friction for a bearing with dry or boundary lubrication, they are not less than those possible by means of a correctly designed thick-film lubricated bearing.
Example. A board carrying a load \(P\) at its midpoint rests on two cylindrical rollers of radius \(r\), as shown in Fig. 2. Find the force \(F\) required to move the board.
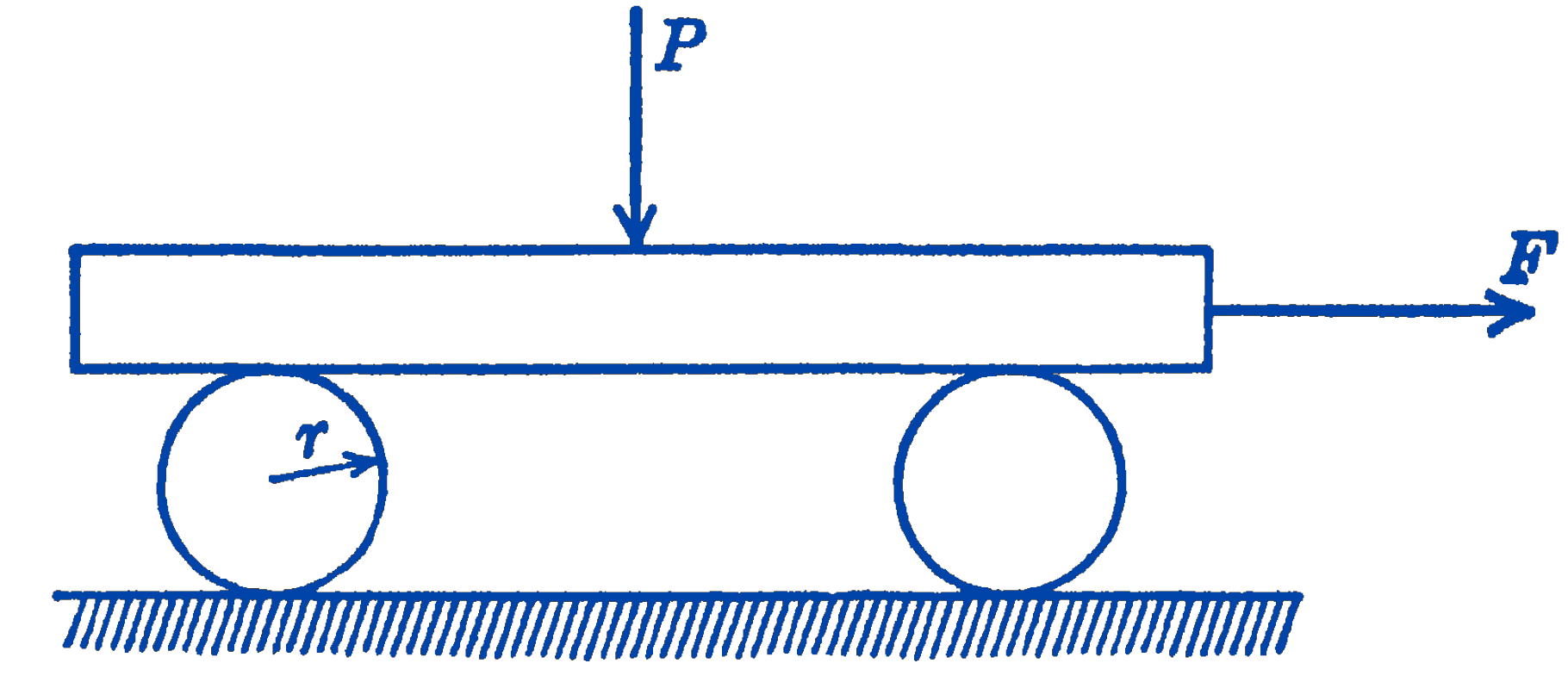
Solution. For one roller the situation is as shown in Fig. 3.
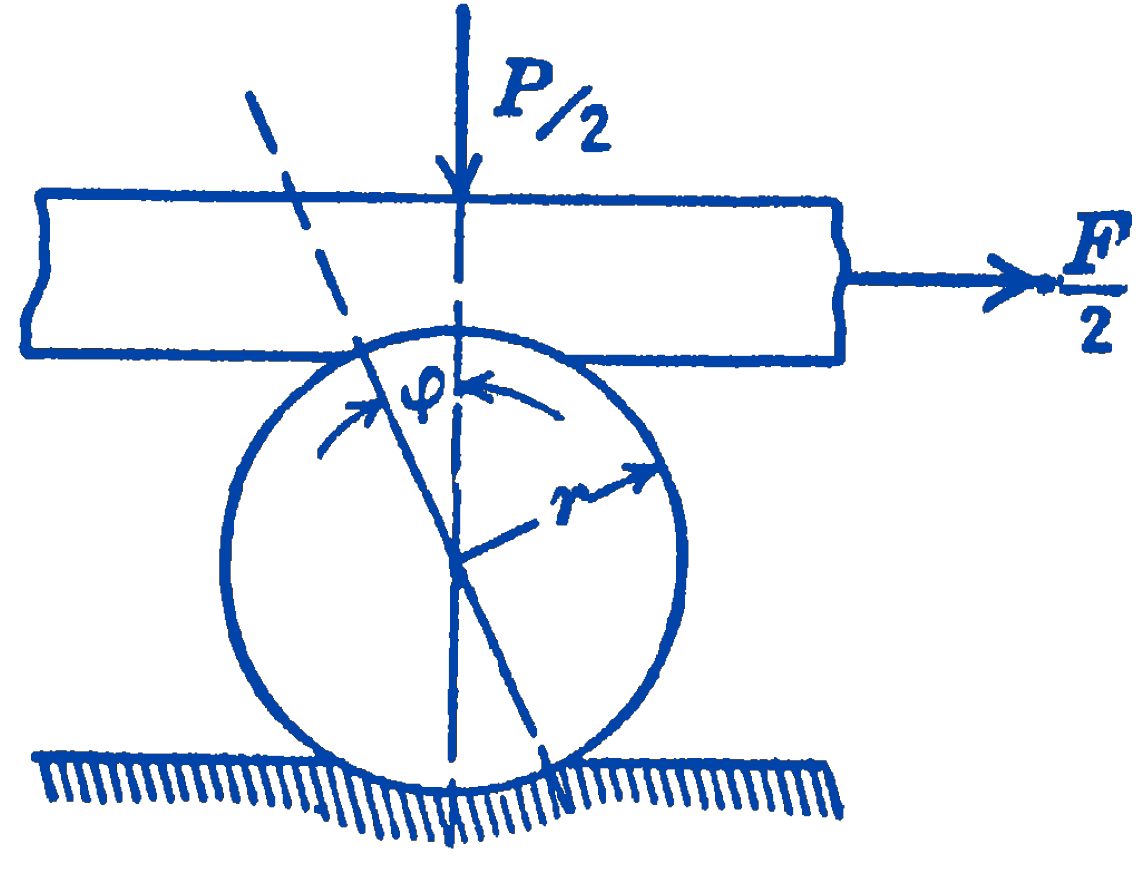
Drawing a free-body diagram (Fig. 4) of the board, we have: \[ \begin{aligned} \sum F_{x} & =0=-N \sin \phi+\frac{F}{2} \\ \sum F_{y} & =0=N \cos \phi-\frac{P}{2} \end{aligned} \]
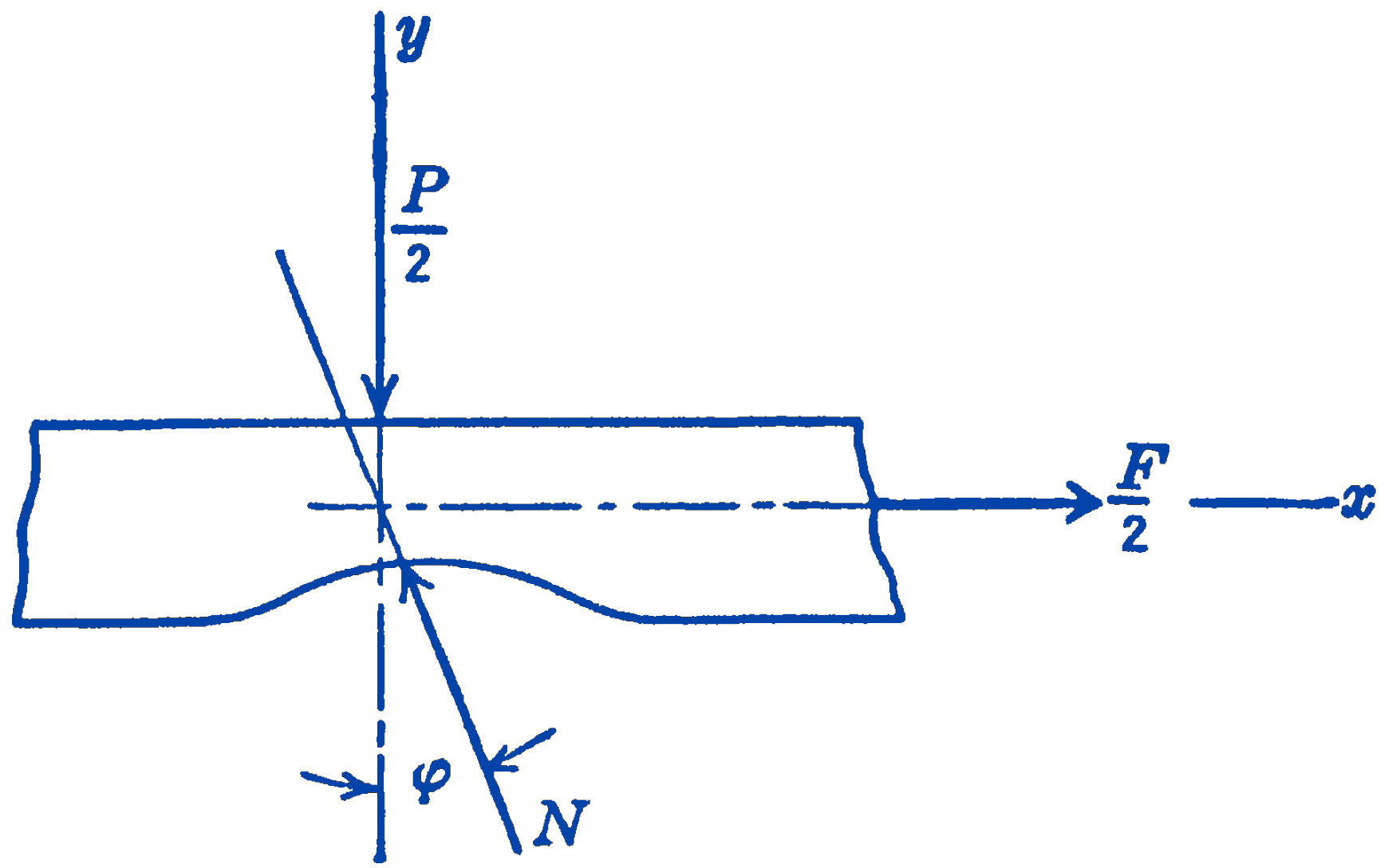
hence: \[ \begin{aligned} & N=\frac{P}{2 \cos \phi} \\ & F=2 N \sin \phi=2 \sin \phi\left(\frac{P}{2 \cos \phi}\right) \\ & F=P \tan \phi \end{aligned} \] For small values of \(\phi\) we have \(\tan \phi \approx \sin \phi\), also \(\sin \phi=\dfrac{a}{r}\), where \(a\) is the “coefficient of rolling resistance,” as defined above; thus \[ F=\frac{P a}{r} \] Note that, although we have in this problem two rolling surfaces, i.e., double-rolling, the same answer is obtained that was found above for single-rolling contact. There are twice the rolling surfaces, but the force is applied in such a position that it is twice as effective in producing rolling motion, so that the net result is the same.
5.3.1 PROBLEMS
1. A house is being moved by pulling it along on planks and wooden rollers as is shown in the diagram. If the total weight of the house is 30,000 lb, find the required horizontal force to move the house at a uniform velocity. The diameter of the rollers is one foot.
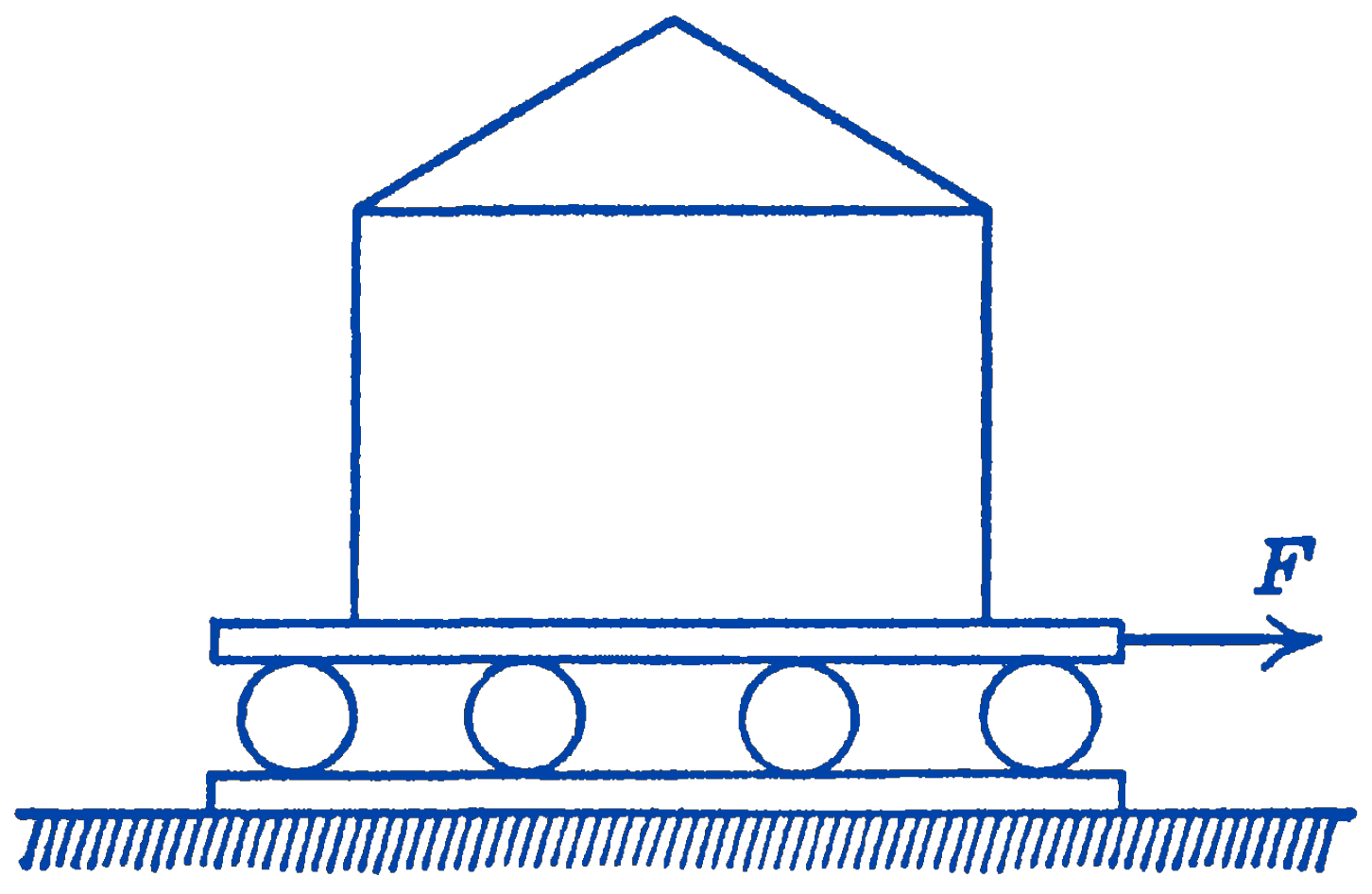
Answer
100 lb (minimum)
2. A straight board is loaded between two sets of rollers as is shown in the accompanying figure. The diameter of the rollers is 3 in., and the coefficient of rolling resistance for all surfaces in contact is 0.01 in . The whole system is loaded vertically by a uniformly distributed load of 2000 lb. Both the top and bottom surfaces are arranged so that they cannot move horizontally. What horizontal force \(F\) is required to move the board?
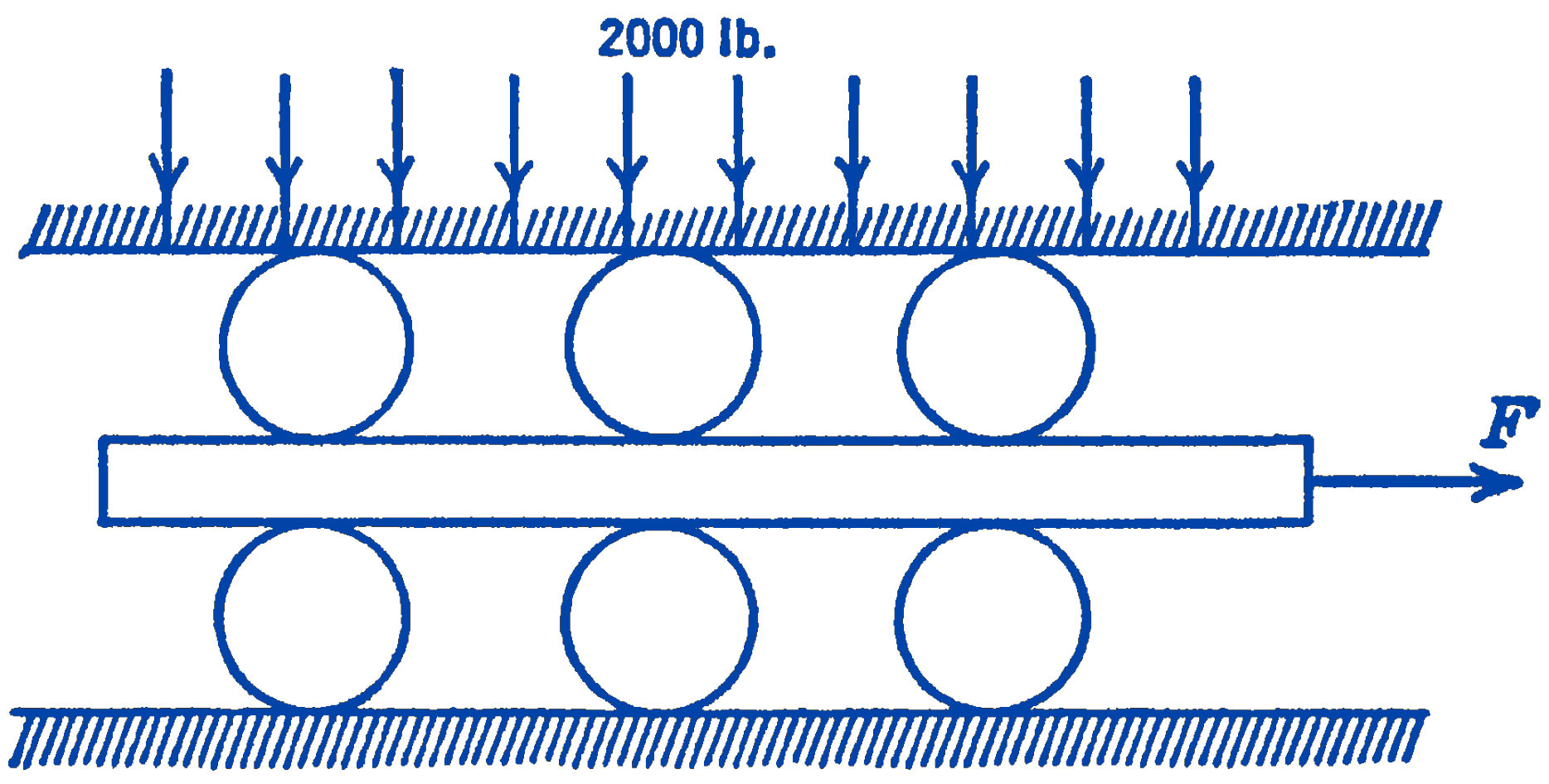
Answer
26.7 lb