Given a circular shaft of radius \(r\) which is loaded by an axial load of \(P\) and is supported by a plane surface as shown in Fig. 1. Find the friction torque set up at the surface.

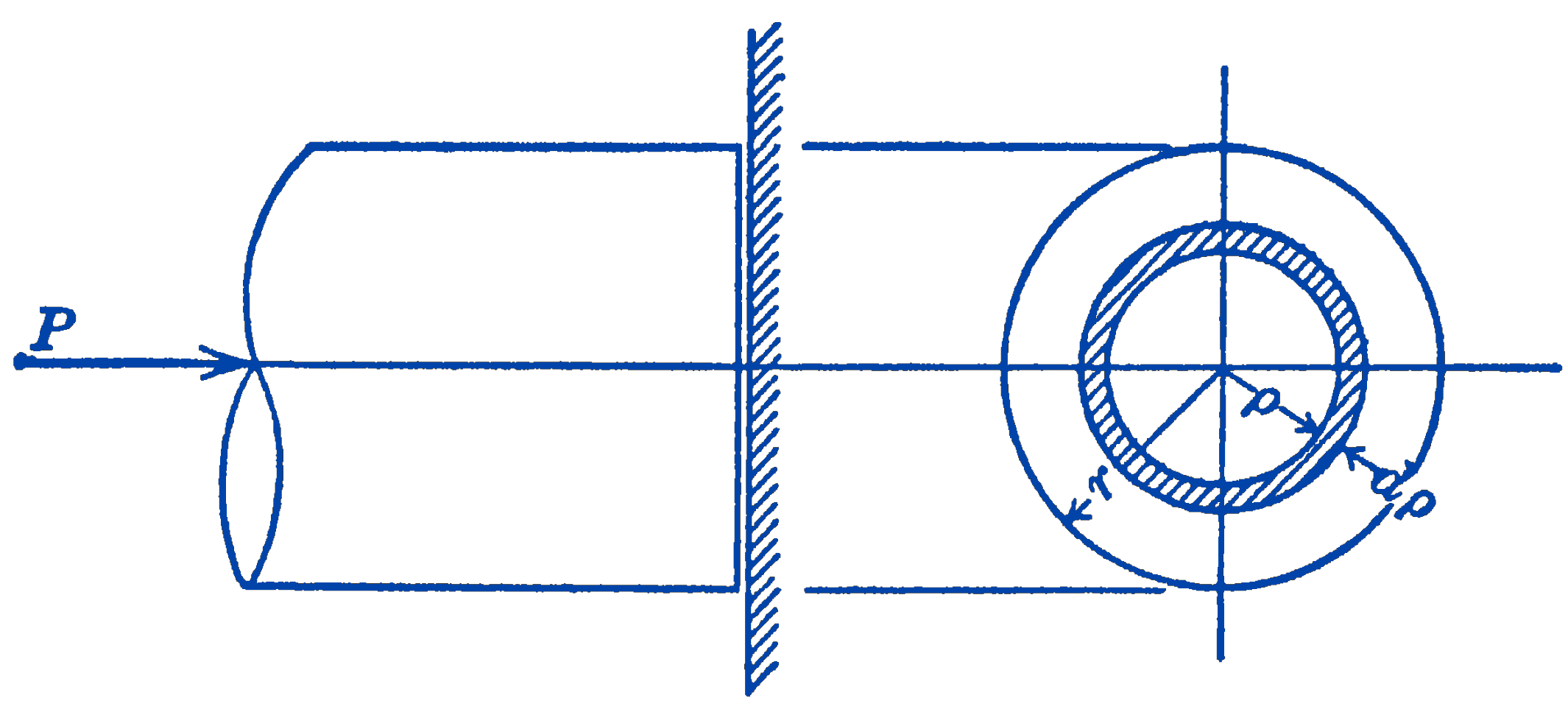
Consider an infinitesimal element in the form of an annular ring of radius \(\rho\) and thickness \(d \rho\). We must now assume some force distribution over the surface. The simplest assumption will be that of a uniform force distribution. Let us say that the unit force or pressure at any point on the surface is \(p\) per unit area. This is related to the total force \(P\) by the fact that: \[ p A=P=p \pi r^{2}. \] The normal force acting on the infinitesimal annular area \(d A\) is equal to: \[ p\, dA=(p)(2 \pi \rho\, d \rho) \] The frictional force tangent to the surface is: \[ d f=\mu p 2 \pi \rho\, d \rho \] The frictional moment about the axis of the shaft, due to the one element shown, is: \[ d M=\rho(\mu p 2 \pi \rho\, d \rho) \] To find the total friction torque we sum up the elements for the whole area: \[ \begin{aligned} M & =2 \pi \mu p \int_{0}^{r} \rho^{2} d \rho=\left.2 \pi \mu p\left(\frac{\rho^{3}}{3}\right)\right|_{0} ^{r} \\ & =2 \pi \mu \frac{P}{\pi r^{2}} \frac{r^{3}}{3}=\frac{2}{3} r \mu P \end{aligned} \] hence, the friction force acts as though it were concentrated at a distance of \(\frac{2}{3} r\) from the center.

If there is relative motion between the shaft and the support surface, for example in a thrust bearing, the above assumption of a constant pressure, which is an approximation in any event, is no longer reasonable. Since the velocity is greater at the outside of the shaft, the friction work done by the elements at large values of \(\rho\) is greater than the friction work done by the elements nearer the center. This causes the outside elements to wear more than the inside elements, and the pressure becomes non-uniform. Let us next solve for the friction torque under the assumption that it is the wear or friction work which is a constant instead of the pressure. We thus make the quantity \(p \rho\) a constant, rather than \(p\) alone. If we call \(p \rho=K\) then the above equation for the friction torque becomes: \[ M=2 \pi \mu K \int_{0}^{r} \rho d \rho=\left.2 \pi \mu K\left(\frac{\rho^{2}}{2}\right)\right|_{0} ^{r}=\pi \mu K r^{2} \] To find the value of \(K\) we note that the sum of all of the normal forces on the elements must be \(P\) : \[ P=\int_{0}^{r} p 2 \pi \rho\, d \rho=2 \pi K \int_{0}^{r} d \rho=2 \pi K r \] so: \[ K=\frac{P}{2 \pi r} \] thus: \[ M=\pi \mu r^{2} \frac{P}{2 \pi r}=\frac{r}{2} \mu P \] hence, under the assumption of constant wear, the friction force acts as though it were concentrated at a distance of \(\dfrac{r}{2}\) from the center.

In most practical problems the coefficient of friction will not be known with sufficient accuracy to justify a distinction between the above two cases.

5.5.1 PROBLEMS

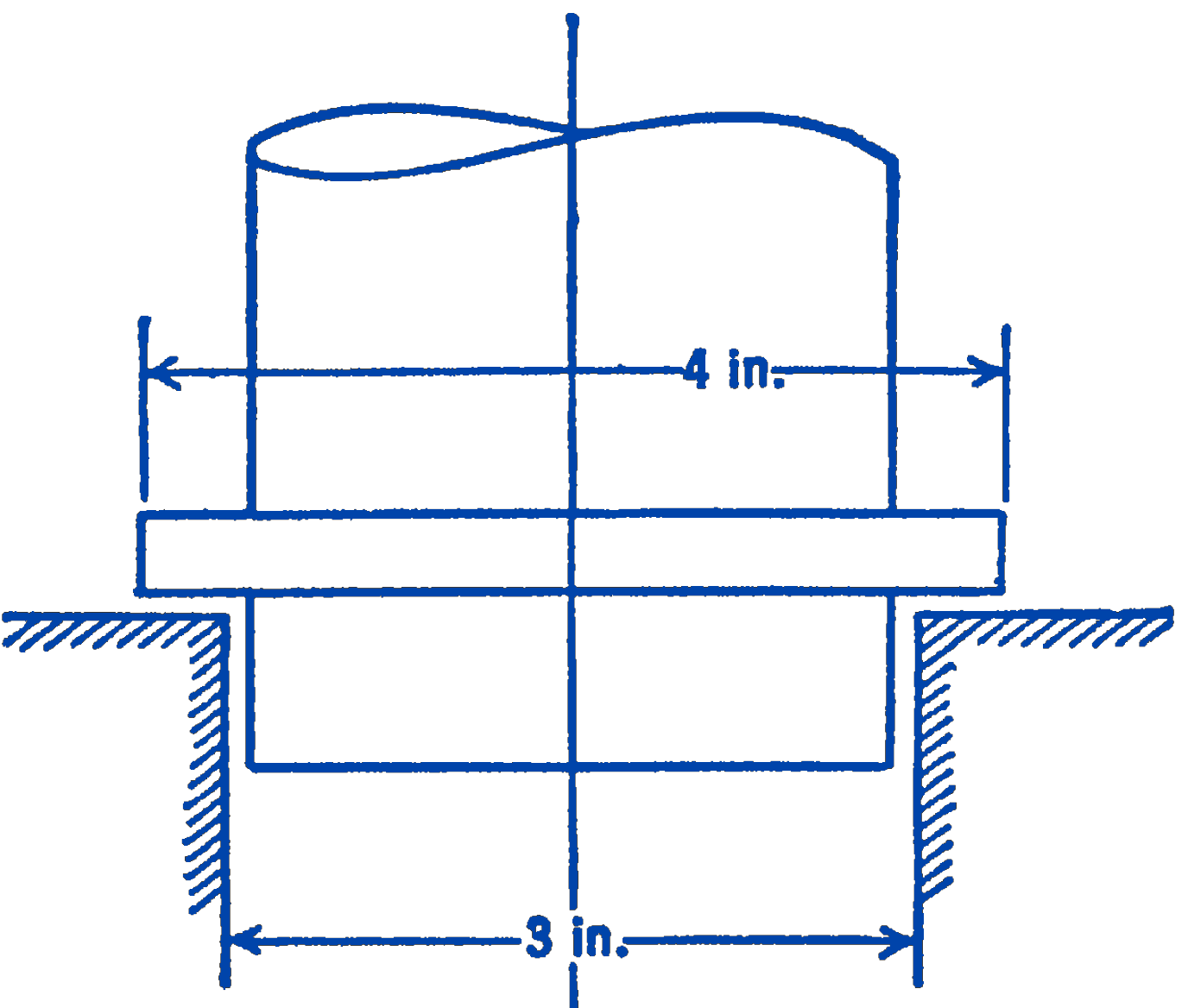
1. A step bearing has the dimensions shown in the diagram. In calculating the energy loss due to friction, how much difference is there between the conclusions based on constant wear and on constant pressure between the bearing surfaces?

Answer

Const. \(p\) gives approx. \(\frac{1}{2} \%\) greater loss

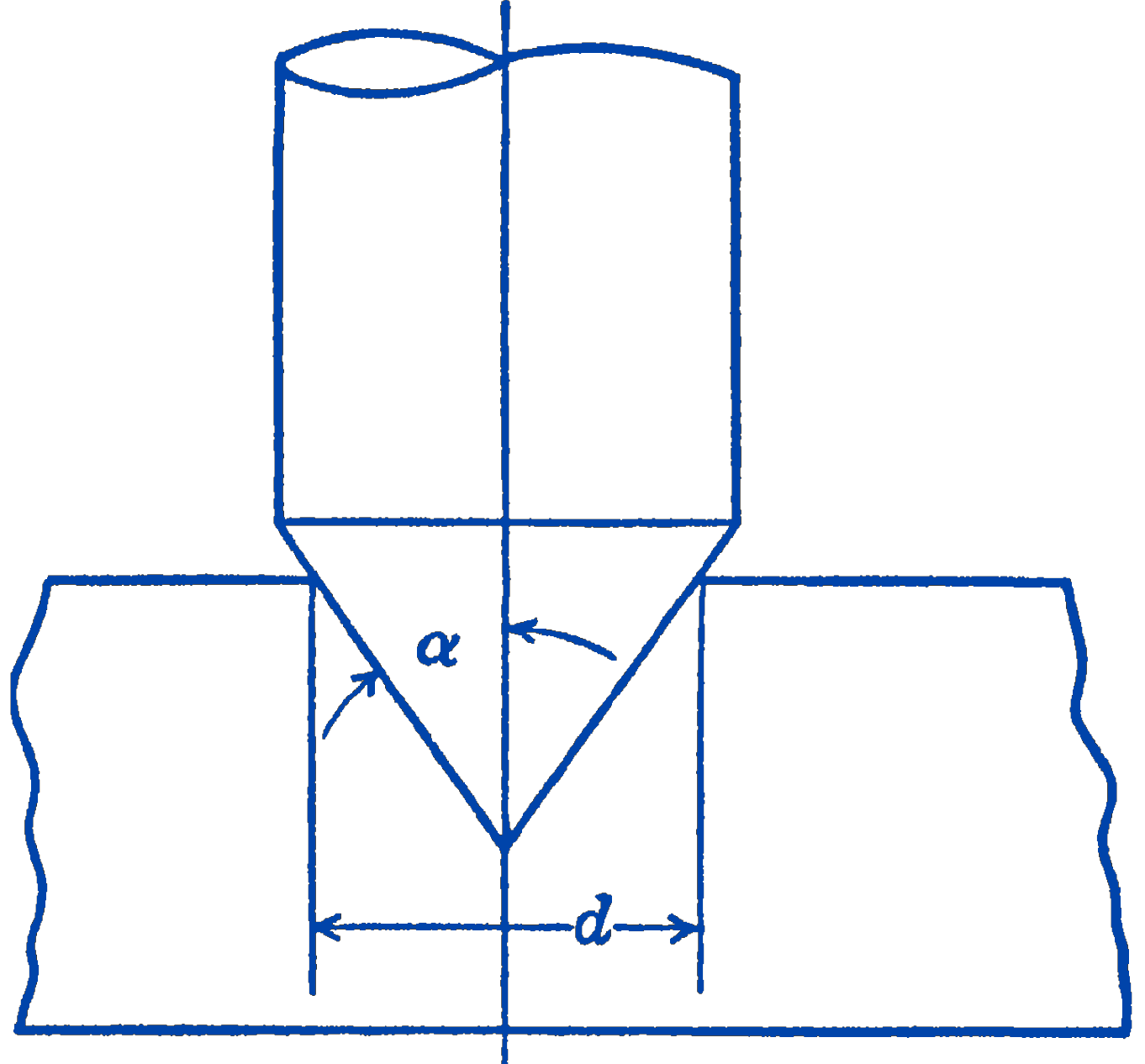
2. Find the friction torque for a conical pivot point as shown in the diagram, assuming that the pressures are uniformly distributed over the surface. Show that for the angle \(\alpha=90^{\circ}\) the result reduces to the case of a plane flat pivot as developed above.

Answer

\(\dfrac{P \mu d}{3 \sin \alpha}\)

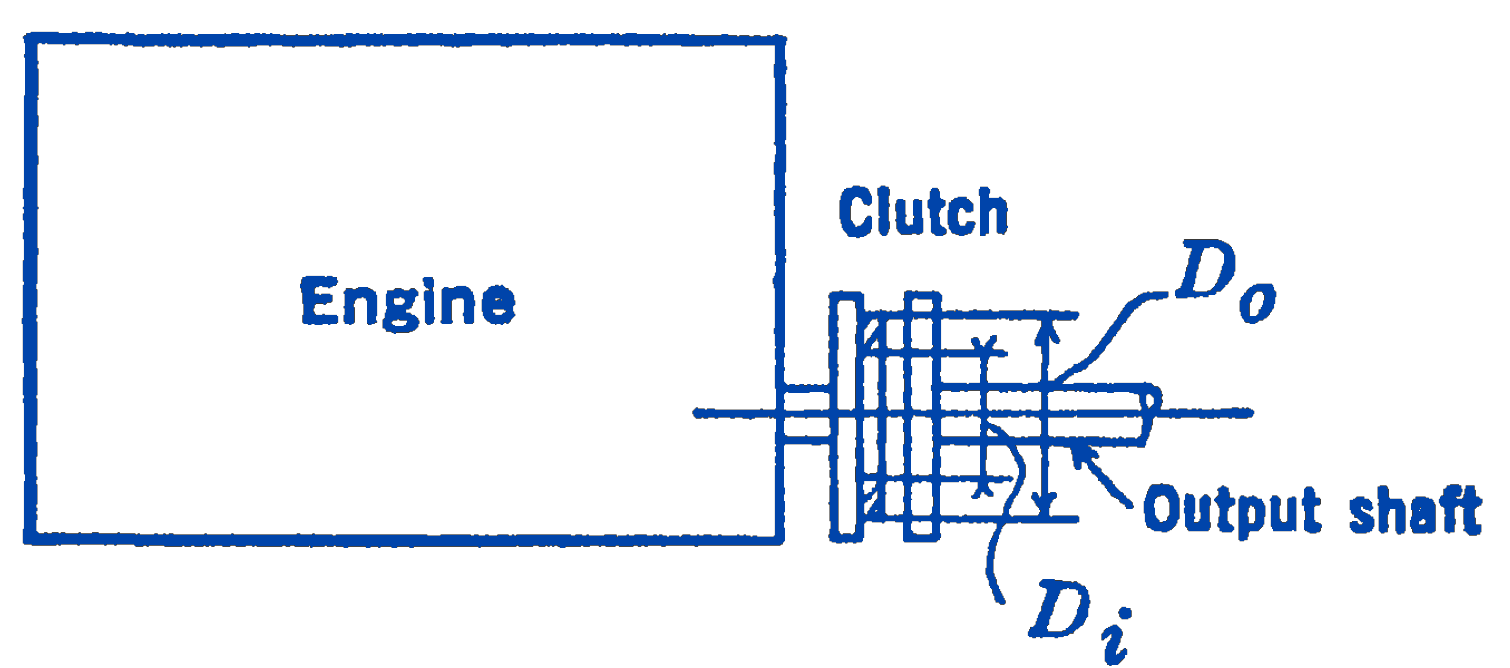
3. A certain automobile engine is capable of developing a maximum torque of 2500 in.-lb. A single plate clutch having the form shown in the diagram is to be designed for the engine.

The torque is transmitted by means of the annular friction surface having an outer diameter \(D_{o}\) and an inner diameter \(D_{i}\). The friction disk has an asbestos facing for which the coefficient of friction is 0.3. If the force per unit area of the disk (assumed to be constant) is to be limited to 30 lb per sq in, and if \(D_{i}=6\ \mathrm{in}\), what should be the value of \(D_{o}\) and what axial force is required to engage the clutch?

Answer

10.8 in., 1900 lb