Consider a block resting on a plane, as shown in Fig. 1. We suppose that the surfaces in contact are clean and dry, and that no lubricating substances are present.

If we apply some very small force \(P\) to the block, our experience tells us that under ordinary conditions the block would not move. This means that there must have been set up at the contact surfaces some reaction force \(F\), which just balances the applied force \(P\). This force \(F\) is physically possible because the surfaces in contact are not absolutely smooth, and, because of small irregularities, a reaction force having a component parallel to the surfaces can be developed. Our experience further tells us that if we increase the load \(P\) we will finally reach a value which will cause the block to move, since it will no longer be possible for a frictional force of sufficient magnitude to be established. This maximum value of frictional force which it is possible to establish, under a given set of conditions, is called the limiting friction and a system which is acted upon by this limiting frictional force is said to be in a state of impending motion, since any further increase in the applied forces would cause motion.
The magnitude of this limiting frictional force has been experimentally determined for a large number of different kinds of contact surfaces, and for various conditions of contact area and normal load.
These experimental facts have been embodied in the laws of dry or Coulomb friction, first stated in a complete way by Coulomb.
- The total amount of friction is independent of the magnitude of the area in contact.
- The total amount of friction is proportional to the normal force.
- For low velocities of sliding the total amount of friction is independent of velocity, and is less than that for impending motion.
These laws are summed up analytically by the following defining equation: \[ \bbox [5px,border:1px #f2f2f2;background-color:#f2f2f2]{F=\mu N} \] where \(F=\) total amount of frictional force parallel to the surfaces in contact, at impending motion, or during motion
\(N=\) total normal force between the surfaces in contact
\(\mu=\) coefficient of friction, which is a constant for given materials
The actual mechanism of dry friction is a complicated one, so that the above laws should be considered as approximations which are sufficiently accurate for most engineering applications.
If the value of \(F\) in the above equation is the limiting value of friction at impending motion, then \(\mu\) is called the coefficient of static friction. It is important to note that the use of this coefficient of static friction gives the maximum magnitude of the frictional force that it is possible to develop between two surfaces under a given normal load and does not necessarily give the actual frictional force present, which may be less than this maximum possible limit.
The following table will indicate some values of the coefficient of static friction which may be obtained under various conditions. It is only possible to indicate a range of values in such a table, since the surface condition plays an important part in the process. It should be emphasized that if any more exact determinations of frictional forces are required for a specific application, it will usually be necessary to determine experimentally the coefficient of static friction under conditions which are as nearly similar as possible to the actual application.
| Coefficients of Static Friction | |
|---|---|
| Wood on wood | 0.25–0.50 |
| Metal on wood | 0.20–0.60 |
| Metal on metal | 0.15–0.30 |
| Metal on leather | 0.30–0.60 |
| Wood on leather | 0.25–0.50 |
In the event that there is sliding motion between the bodies, the coefficient of kinetic friction is used to find the friction force. This coefficient of kinetic friction depends so much, however, upon the velocity, the presence of material which may act as a lubricant, etc., that it is not possible to give even approximate values in the form of a table.
Since the relationship between the dry static friction force and the normal force is known once the coefficient of static friction is known, the angle between the normal and the total reaction force at the surface of contact can be determined. The relationship between this angle of friction and the coefficient of friction is shown in Fig. 2: \[ \tan \phi=\frac{F}{N}=\mu. \] This angle of friction determines the direction of the resultant reaction force.

There are two types of problems involving dry friction which commonly occur in statics. In the first type of problem, one of the conditions of the physical problem is that motion is impending, and the relationship between the forces is required. For such problems it is known that the maximum possible static frictional forces exist, so that the relationship between the frictional forces and the normal forces is directly given by the coefficient of static friction. In the other type of problem the forces acting on the system are given, and it is desired to know whether the frictional forces can maintain equilibrium of the system. Since in this case frictional forces less than the maximum may suffice to maintain equilibrium, one does not know that the friction forces are given by the normal force times the coefficient of static friction. In this case the usual approach is to determine the coefficient of static friction necessary to maintain equilibrium. By then comparing this calculated coefficient with the coefficient which is possible for the given problem, one can tell whether or not equilibrium will be possible.
Example 1. A block of weight \(W\) rests on an inclined plane (Fig. 3). The coefficient of static friction between the block and the plane is \(\mu\). Find the angle \(\alpha\) for impending motion down the plane.
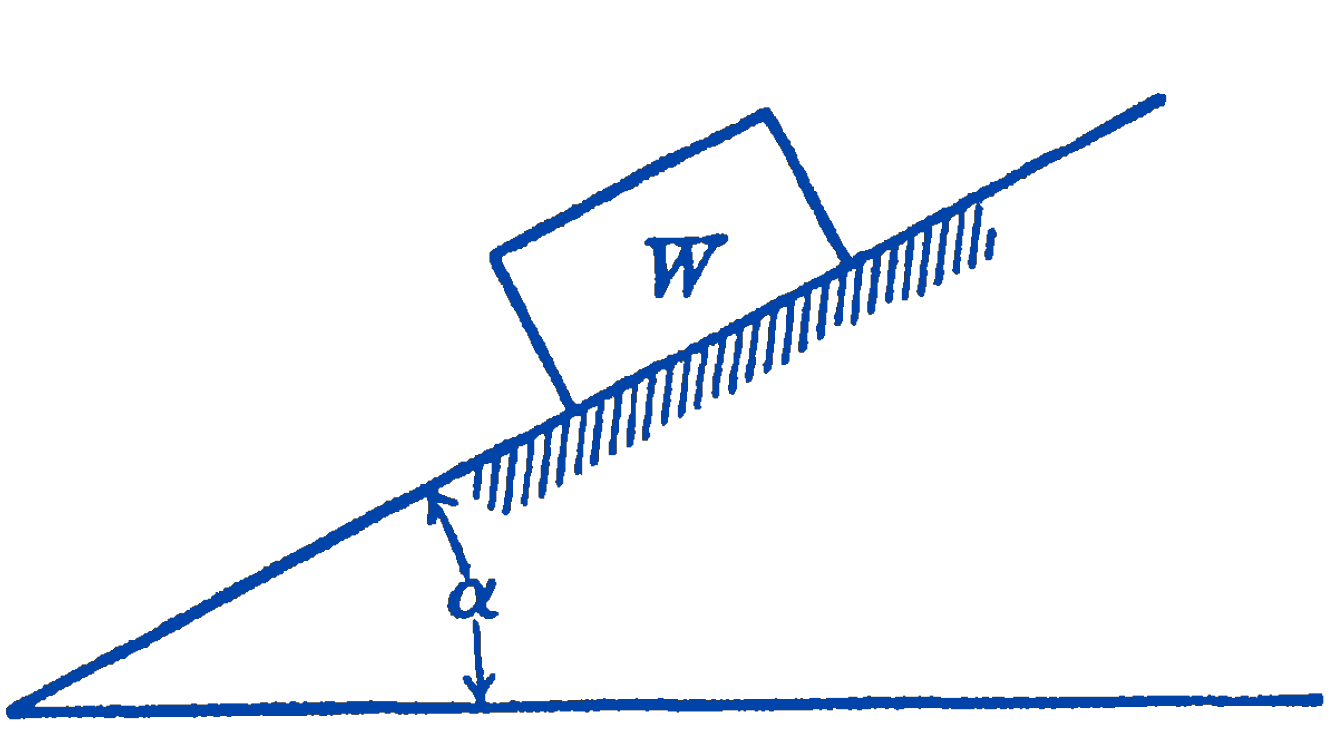
Solution. Drawing a free-body diagram (Fig. 4), and taking the coordinate system parallel and normal to the plane, we have for equilibrium: \[ \begin{aligned} & \sum F_{x}=0=F-W \sin \alpha, \\ & \sum F_{y}=0=N-W \cos \alpha. \end{aligned} \]
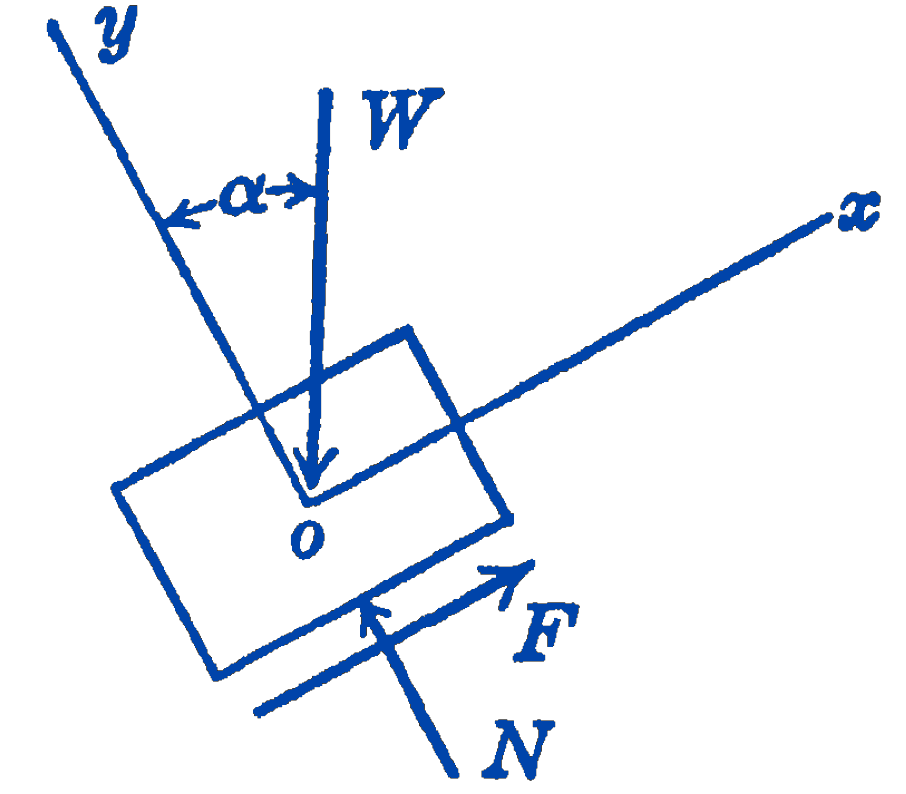
Since motion is impending \[ F=\mu N \] so \[ \frac{F}{N}=\tan \alpha=\mu \] or, since \(\mu=\tan \phi\) where \(\phi=\) the angle of friction \[ \alpha=\phi \] The angle \(\alpha\) is called the angle of repose.
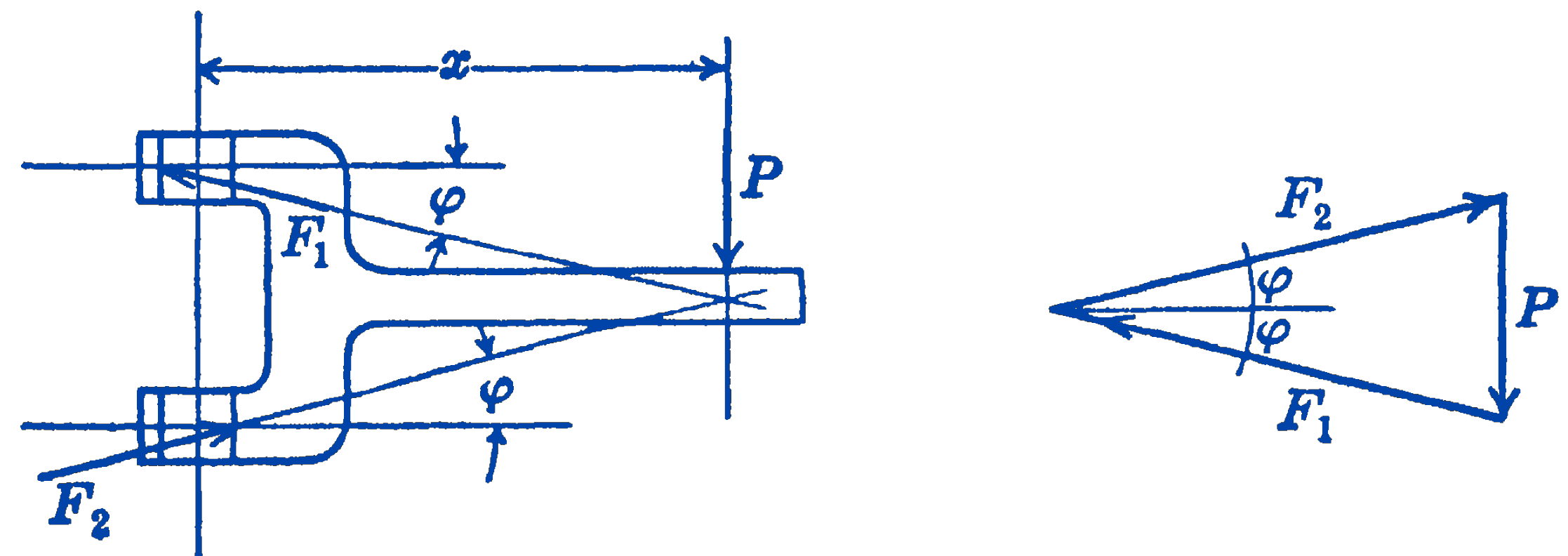
Example 2. A load \(P\) is carried on a bracket which slides on a vertical member as shown in Fig. 5. At what distance \(x\) from the support should the load be placed in order that motion shall be impending? Neglect the weight of the bracket, and assume that there is dry friction between the bracket and the support with a coefficient of static friction equal to 0.25 .
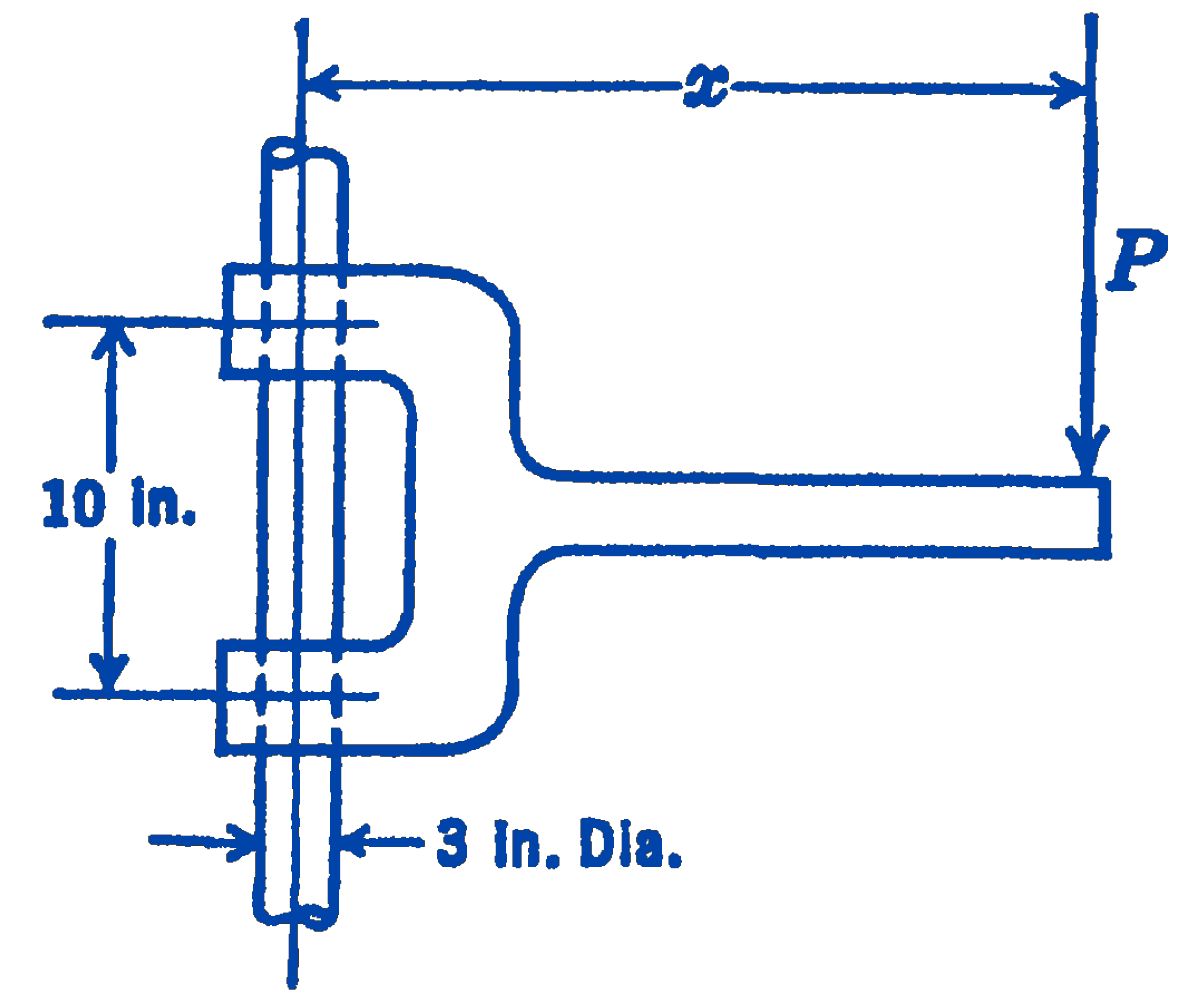
Solution. Drawing a free-body diagram (Fig. 6) and writing the equations of equilibrium, we have: \[ \begin{aligned} \sum F_{x} & =0=-N_{1}+N_{2} ; \quad N_{1}=N_{2} \\ \sum F_{y} & =0=F_{1}+F_{2}-P \\ \sum M_{O} & =0=(10)\left(N_{1}\right)-(3)\left(F_{1}\right)-(x-1.5)(P) \end{aligned} \]
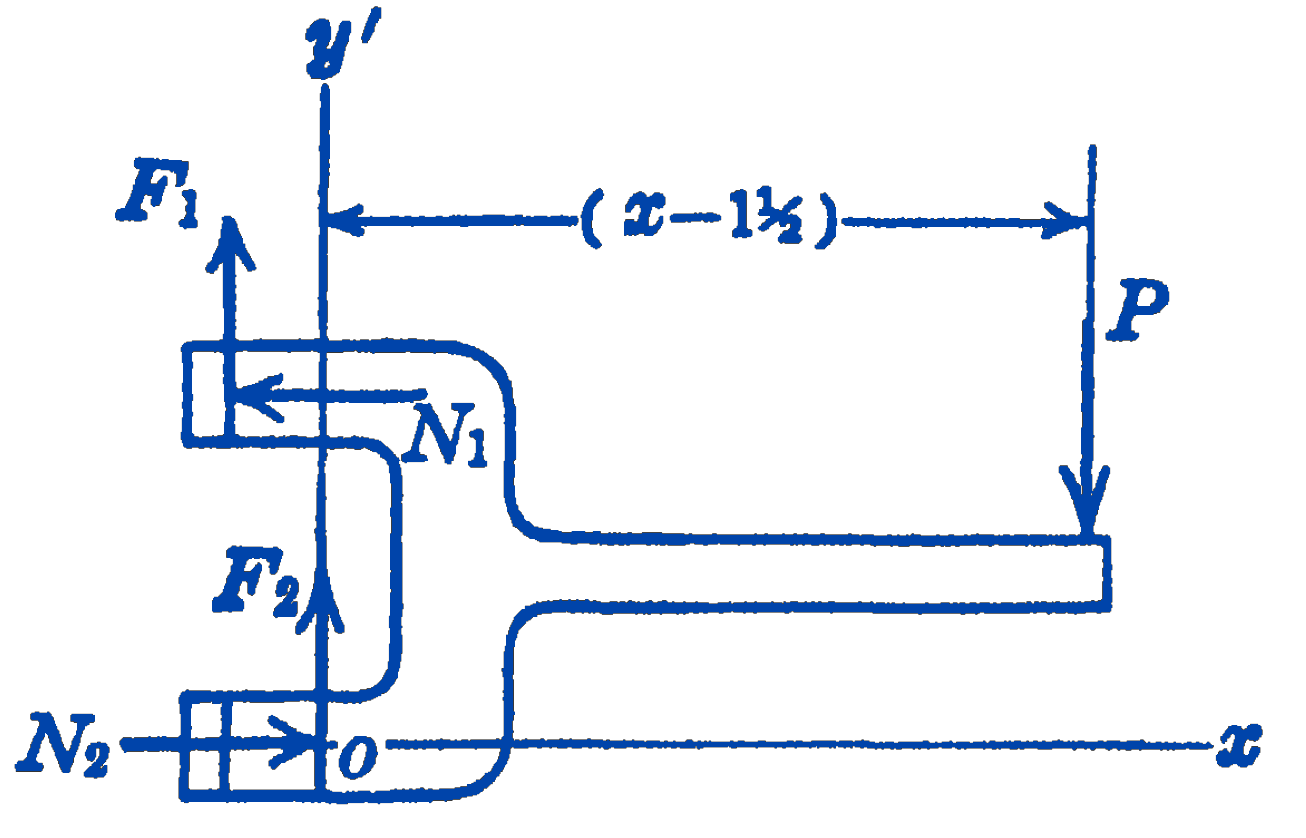
Since motion is impending, we also have: \[ \begin{aligned} & F_{1}=0.25 N_{1} \\ & F_{2}=0.25 N_{2} \end{aligned} \] Hence: \[ \begin{aligned} & P=F_{1}+F_{2}=0.5 N_{1} \\ & 10 N_{1}-0.75 N_{1}-(x-1.5)\left(0.5 N_{1}\right)=0 \\ & 10-0.75+0.75=0.5 x \\ & x=20\ \mathrm{in}. \end{aligned} \] By using the idea of the angle of friction, a graphical solution of this problem can be obtained. If the reaction forces are shown in their proper directions, instead of as two components, the force system will consist, of three non-parallel coplanar forces, which must be concurrent if they are to be in equilibrium (Fig. 7).
Example 3. The block \(W_{1}\) weighs 100 lb , and the block \(W_{2}\) weighs 50 lb (Fig. 8). The coefficient of static friction between the upper block and the lower block is 0.35 , and between the lower block and the horizontal plane is 0.1 . A horizontal force of 20 lb acts upon the upper block as shown in the diagram. Find the force in the cable \(A B\) for equilibrium of the lower block.
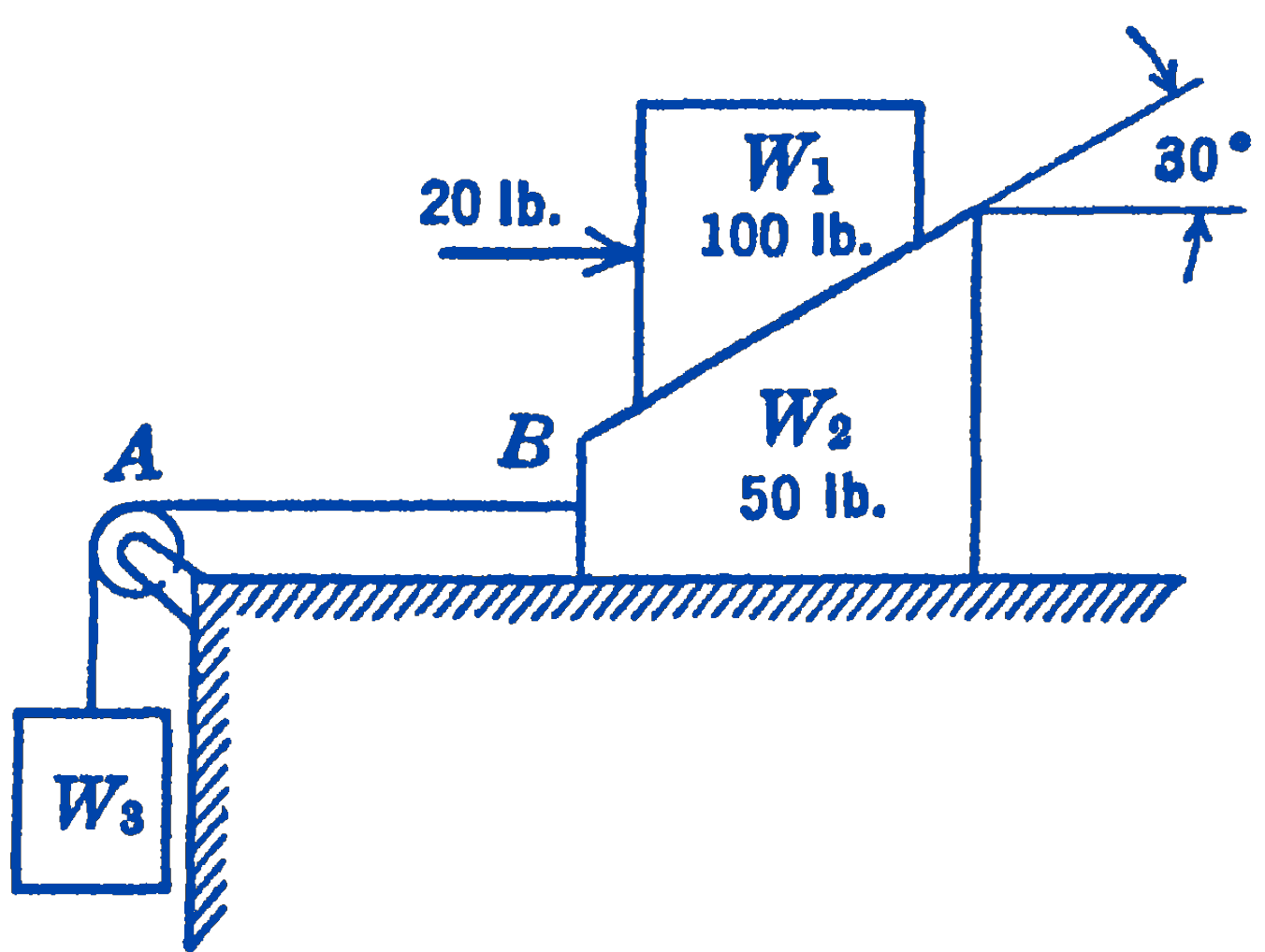
Solution. Since we do not know that the top block is in equilibrium or that motion of this top block is impending, we cannot immediately write down the equations of equilibrium. We must first check to see whether equilibrium is possible, or whether the upper block will move. Let us compute the coefficient of static friction which would just suffice to keep the upper block in equilibrium, i.e., which corresponds to impending motion. It will be seen that if there were no friction force, the upper block would move down the lower block, so that we would have impending motion downward.
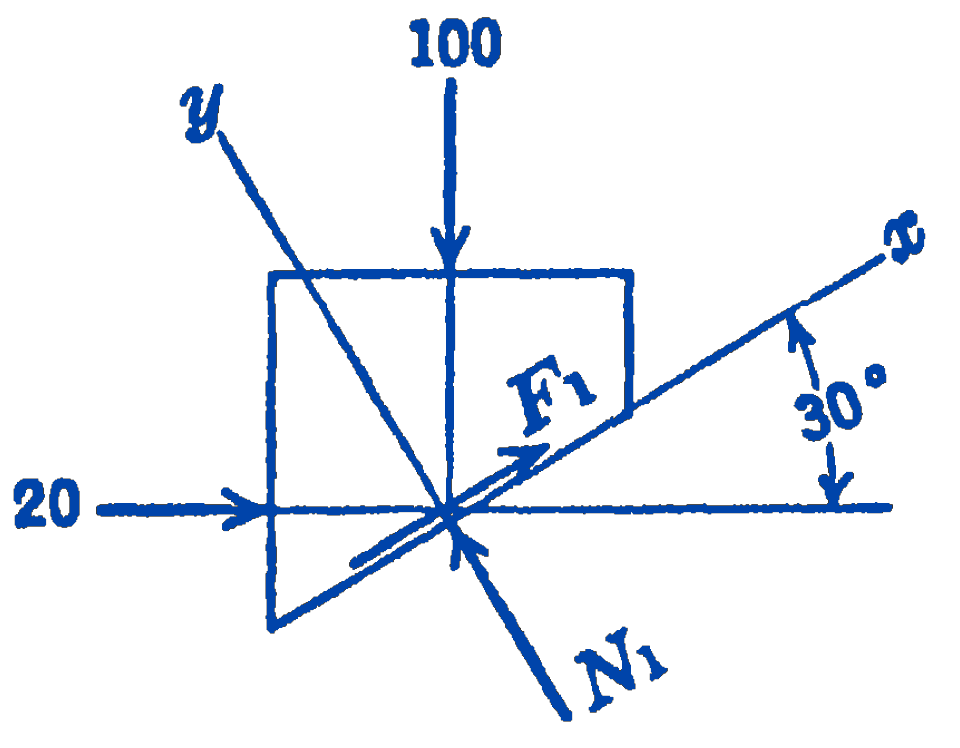
\[ \begin{aligned} \sum F_{x} & =0=20 \cos 30^{\circ}-100 \sin 30^{\circ}+F_{1} \\ \sum F_{y} & =0=-20 \sin 30^{\circ}-100 \cos 30^{\circ}+N_{1} \\ F_{1} & =\mu N_{1} \\ F_{1} & =-(20)(0.866)+(100)(0.5)=32.7\ \mathrm{lb} \\ N & =(100)(0.866)+(20)(0.5)=96.6\ \mathrm{lb} \\ \mu & =\frac{32.7}{96.6}=0.338 \end{aligned} \] Since this friction required for equilibrium is less than that actually present, we know that equilibrium exists. Furthermore, motion is not impending, and the above value of computed friction force (32.7 lb) is the actual value existing, although it is not the maximum value which could exist.
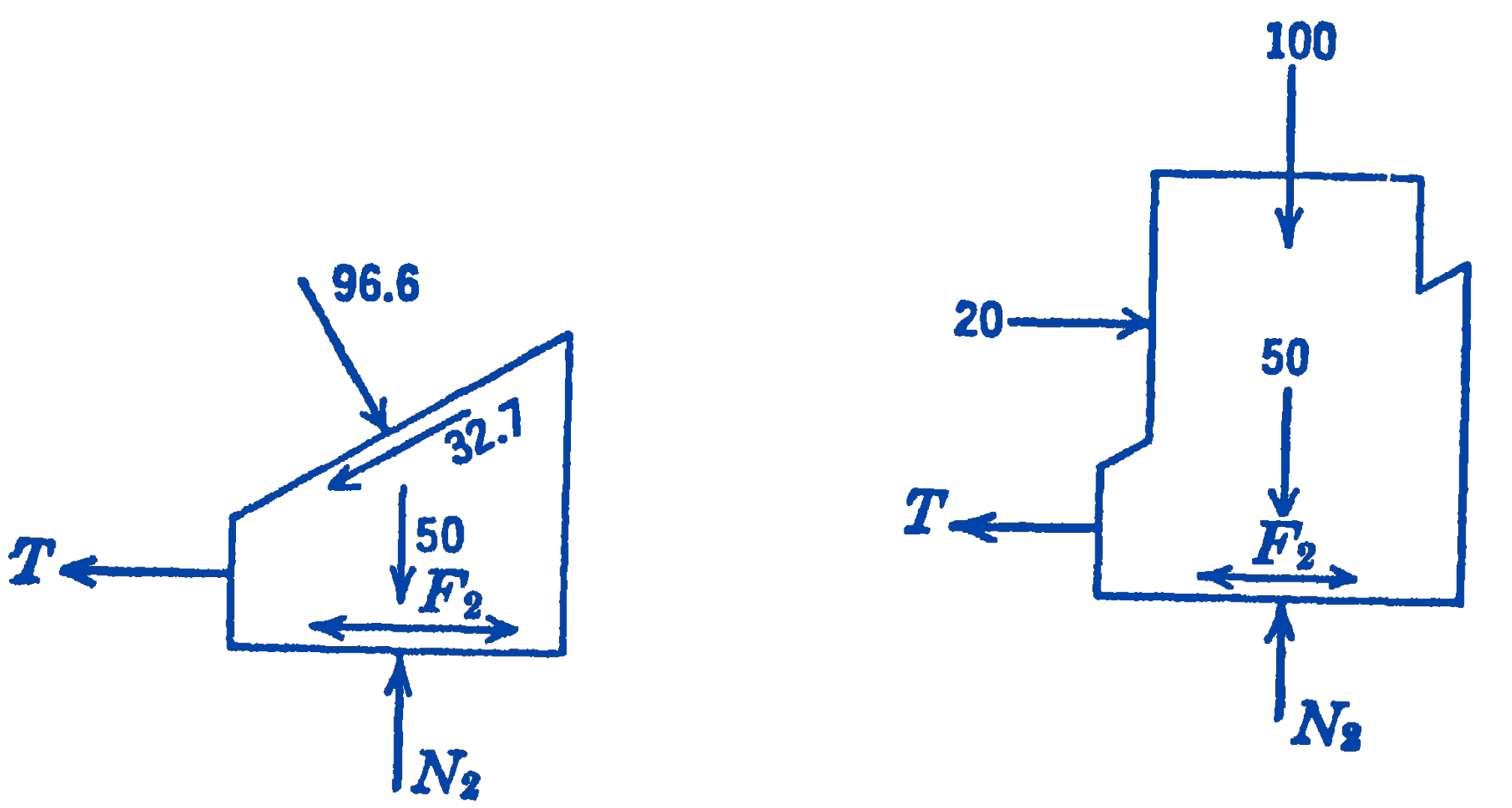
Similarly for analysis of the lower block we have the free-body diagrams shown in Fig. 10. Motion of the lower block might be impending in either direction, and still the system would be in equilibrium. There will thus be a range of values of the force \(T\) which could maintain equilibrium.
Assuming motion impending to the left, we have, considering the free-body diagram of the whole body: \[ \begin{aligned} \sum F_{x} & =0=-T+F_{2}+20 \\ \sum F_{y} & =0=N_{2}-50-100 ; \quad N_{2}=150\ \mathrm{lb} \\ F_{2} & =0.1 N_{2}=15\ \mathrm{lb} \\ T & =15+20=35\ \mathrm{lb} \end{aligned} \] Assuming motion impending to the right, we have: \[ \begin{aligned} \sum F_{x} & =0=-T-F_{2}+20 \\ T & =20-F_{2}=20-15 \\ T & =5\ \mathrm{lb} \end{aligned} \] Hence any value of \(T\) between 5 and 35 lb will keep the system in equilibrium. For intermediate values, motion will not be impending, and the magnitude of the friction force will not be its maximum possible value, but will be that required for equilibrium.
5.1.1 PROBLEMS
1. A ladder weighing 75 lb rests against a vertical wall at an angle of \(30^{\circ}\) with the wall. If the coefficient of static friction between the ladder and the wall and floor is 0.25, how far up the ladder can a 160 lb man climb without slipping of the ladder?
Answer
\(0.45 l\)
2. A 2-in thick slab is to be rolled between two 24-in diameter rolls. If the coefficient of kinetic friction between the rolls and the hot metal is 0.15 , what is the minimum spacing \(a\) between the rolls for which the forces exerted on the slab by the rolls at first contact will be in such a direction as to pull the slab into the rolls?
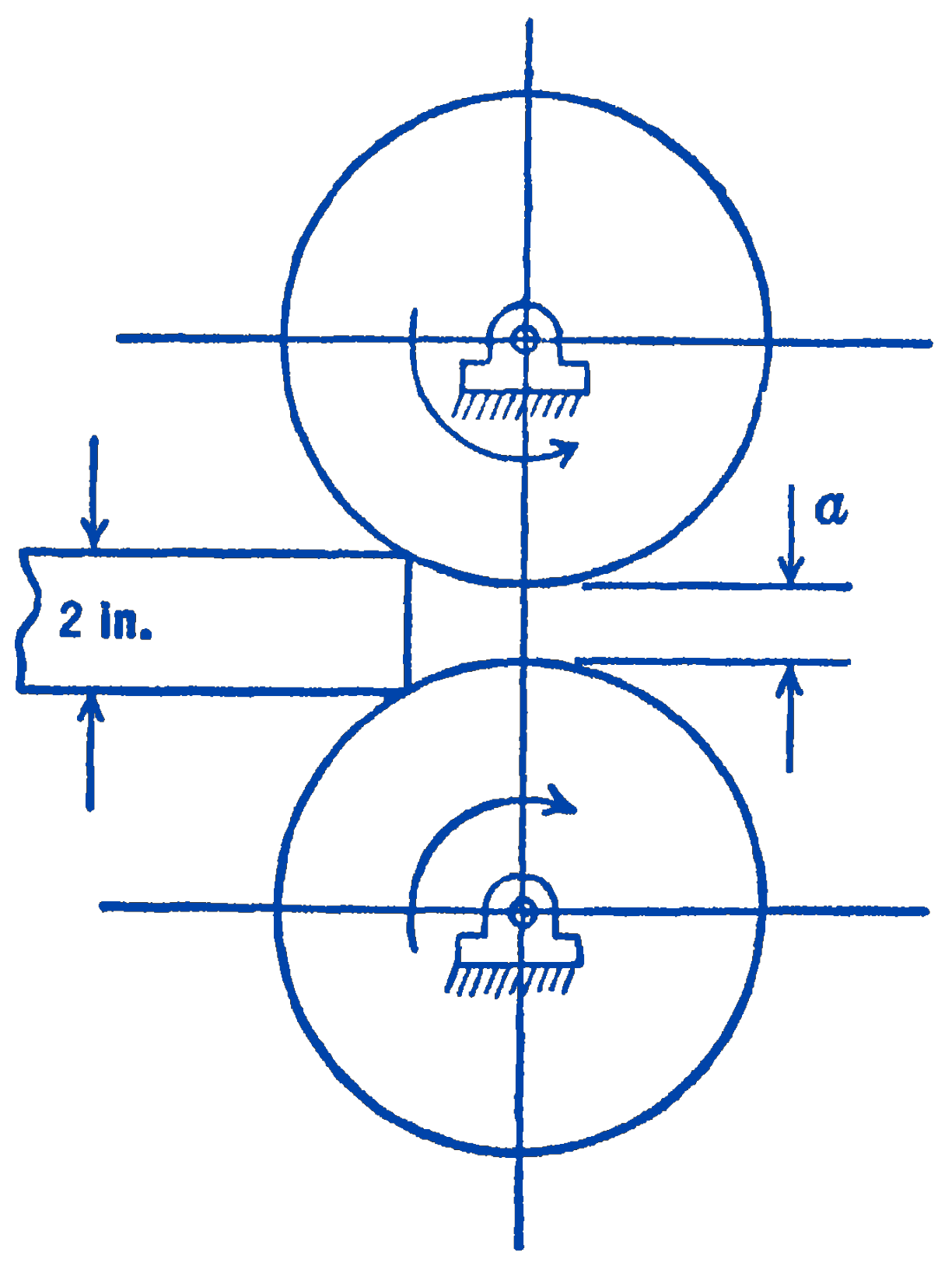
Answer
1.73 in
3. A round bar loaded with a 1000-lb weight passes through a plate and is supported by means of a “cotter key” through a slot in the round bar. Assuming that the coefficient of static friction between the key and the bar, between the key and the plate, and between the bar and the plate, is 0.25 , find the maximum angle \(\alpha\) for which the device is self-locking, i.e., for which the load does not force the key out of the slot.
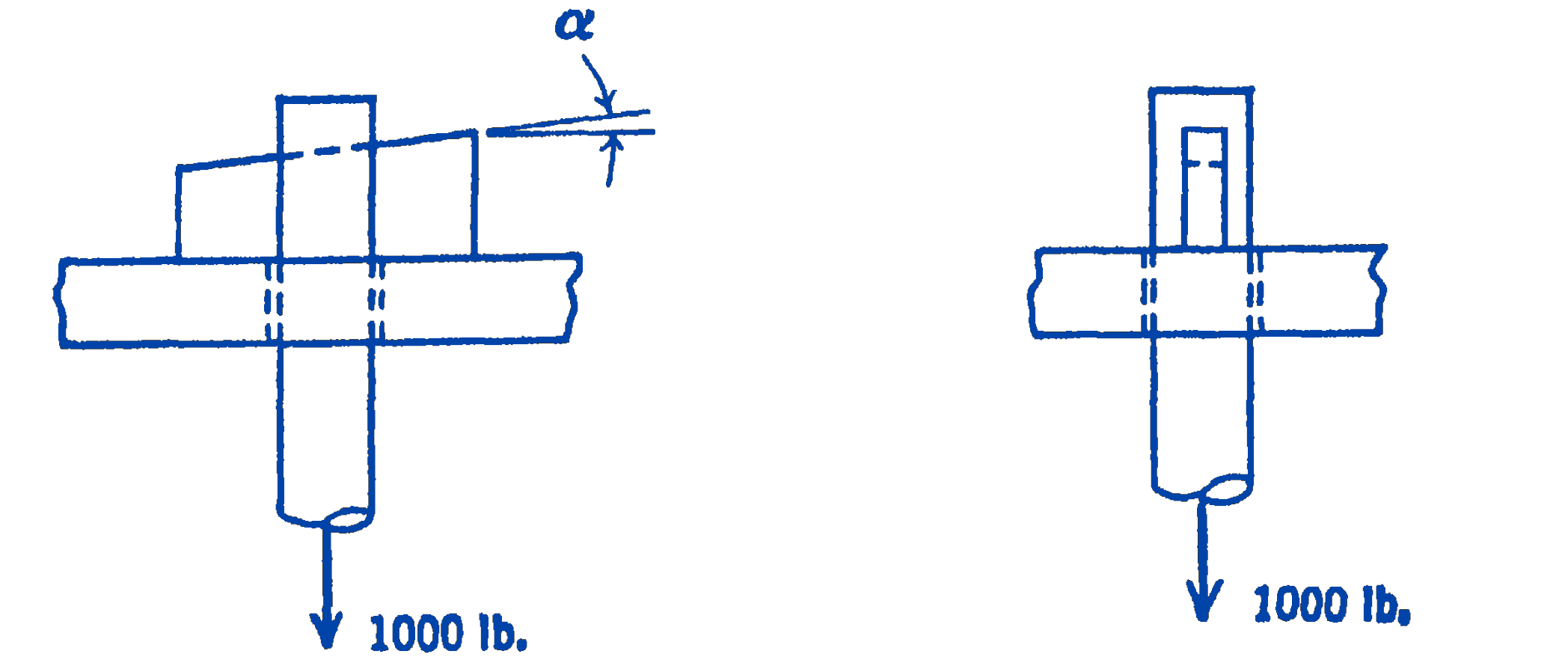
Answer
\(\alpha=\tan ^{-1}\left(\frac{8}{15}\right)\)
4. If the angle \(\alpha\) of the key in Problem 120 above is \(12^{\circ}\), find the force necessary to withdraw the key from the slot.
Answer
286 lb
5. One type of free wheeling clutch is shown in the figure. If the inside member is rotated counterclockwise, the rollers are jammed between the inclined surfaces and hence drive the outer member. If the inner member is rotated clockwise, the rollers are pulled free and do not drive the outer member. The situation for each roller is somewhat as shown in the following diagram.
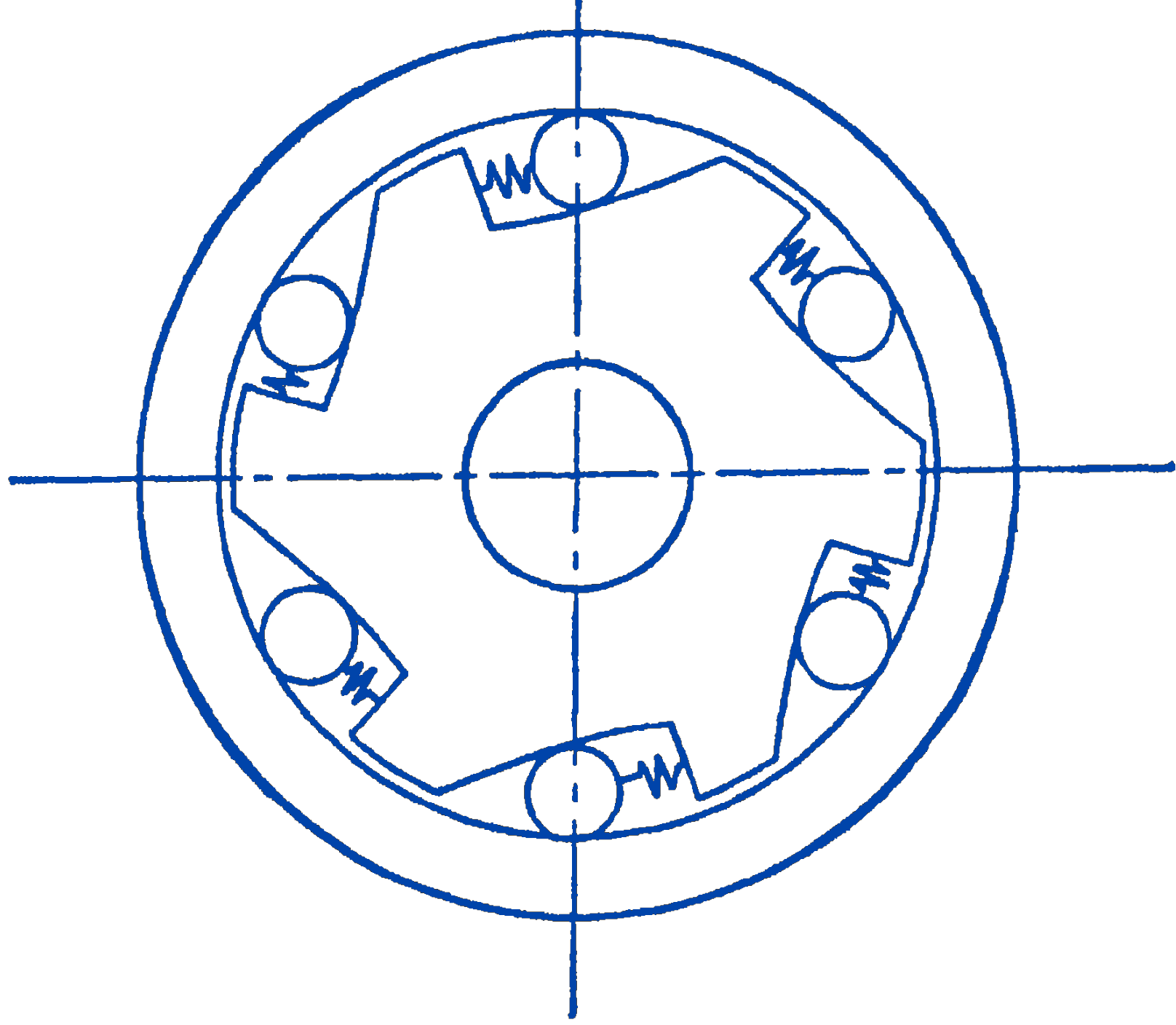
If the angle between the two surfaces is too great, as in (a), the roller would be just pushed along the lower surface. If the angle is too small, as in (b), the roller will jam itself between the two surfaces and will be difficult to release. If the coefficient of static friction for the hardened steel rollers and surfaces is 0.08 , find the maximum angle \(\alpha\) which could be used for such a clutch.
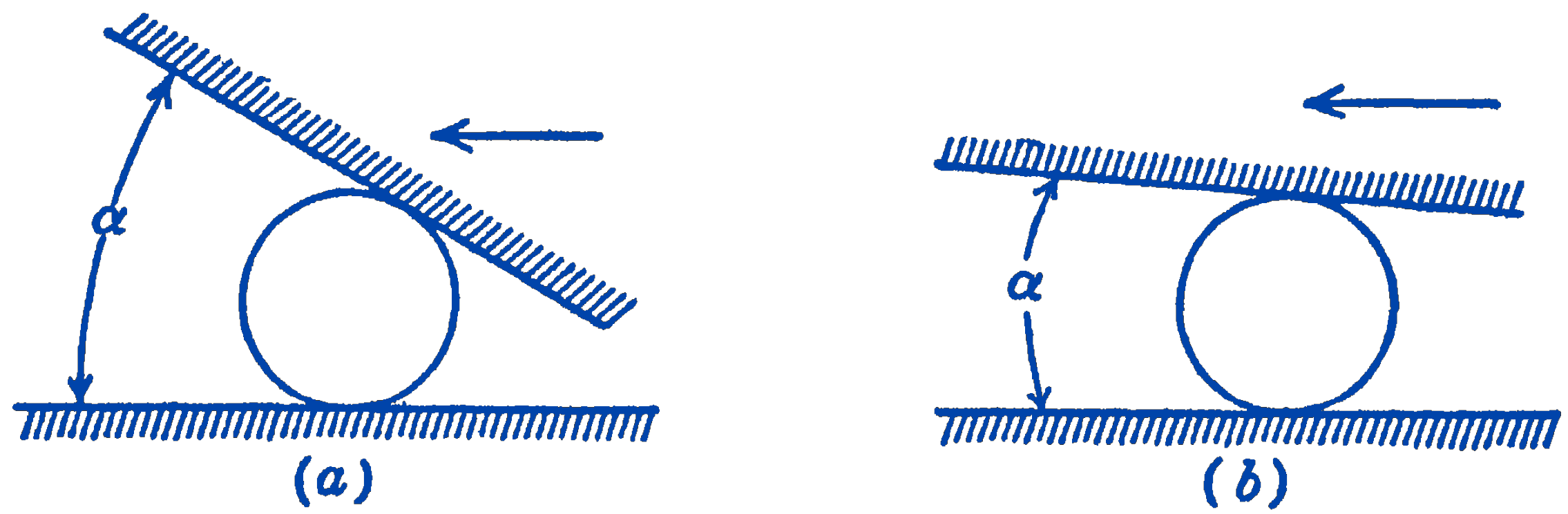
Answer
\(\alpha=2 \tan ^{-1} \mu=9^{\circ} 10^{\prime}\)
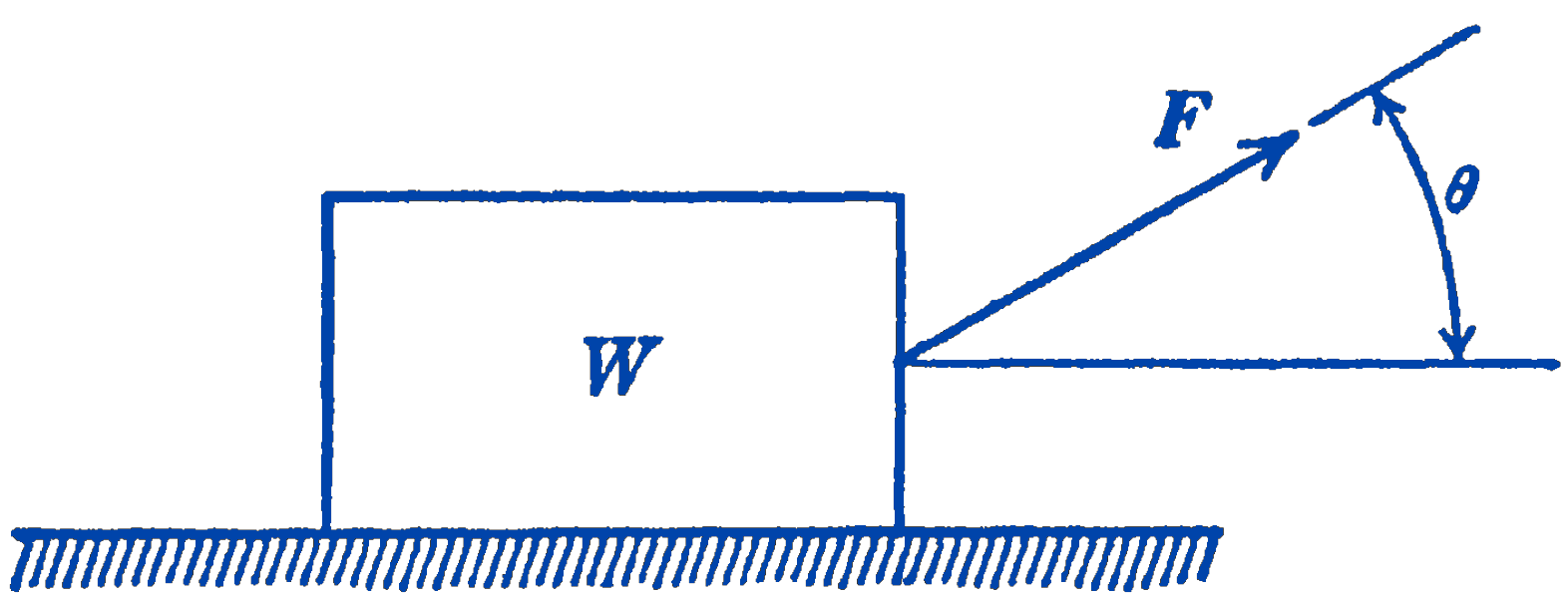
6. A block of weight \(W\) rests on a rough horizontal plane and is loaded by a force \(F\) making an angle \(\theta\) with the horizontal. Show that the minimum value of \(F\) is required for impending motion when the angle \(\theta\) is equal to the friction angle.
7. An insect climbs up the side of a hemispherical bowl. If the coefficient of static friction between the legs of the insect and the bowl is 0.30 , how high can the insect climb?
Answer
\(0.043 R\)
8. A force \(P\) is applied to one handle of a drawer. Assuming that the reactions are concentrated at the points \(A\) and \(B\), find the maximum distance a at which the drawer could be pulled open, for a given coefficient of static friction \(\mu\). Neglect friction on the bottom of the drawer.
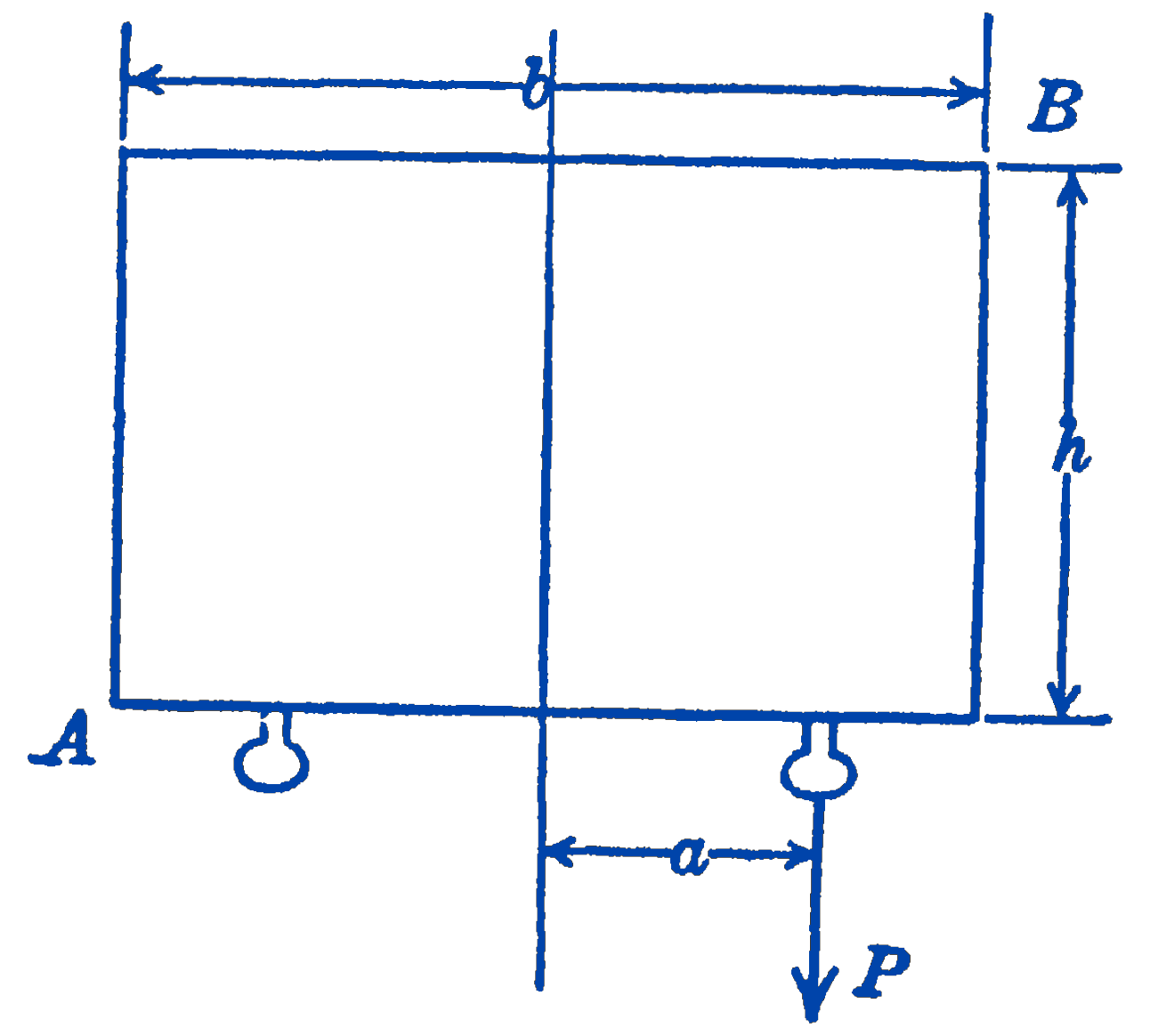
Answer
\(a=\dfrac{h}{2 \mu}\)
9. A uniform rectangular block of dimensions 4 in by 4 in by 10 in rests on a horizontal board, with the large dimension normal to the board. The coefficient of static friction between the block and the board is 0.25. If the board is gradually tilted through an increasing angle, will the block slide or tip?
Answer
Slide
10. A load \(P\) is to be raised by a system of wedges loaded by forces \(F\) as shown in the diagram. If the coefficient of static friction is 0.25 for all surfaces in contact, find the relationship between \(F\) and \(P\) to raise the load and to lower the load. Is the system self-locking; i.e., if the forces \(F\) are removed, is \(P\) supported?
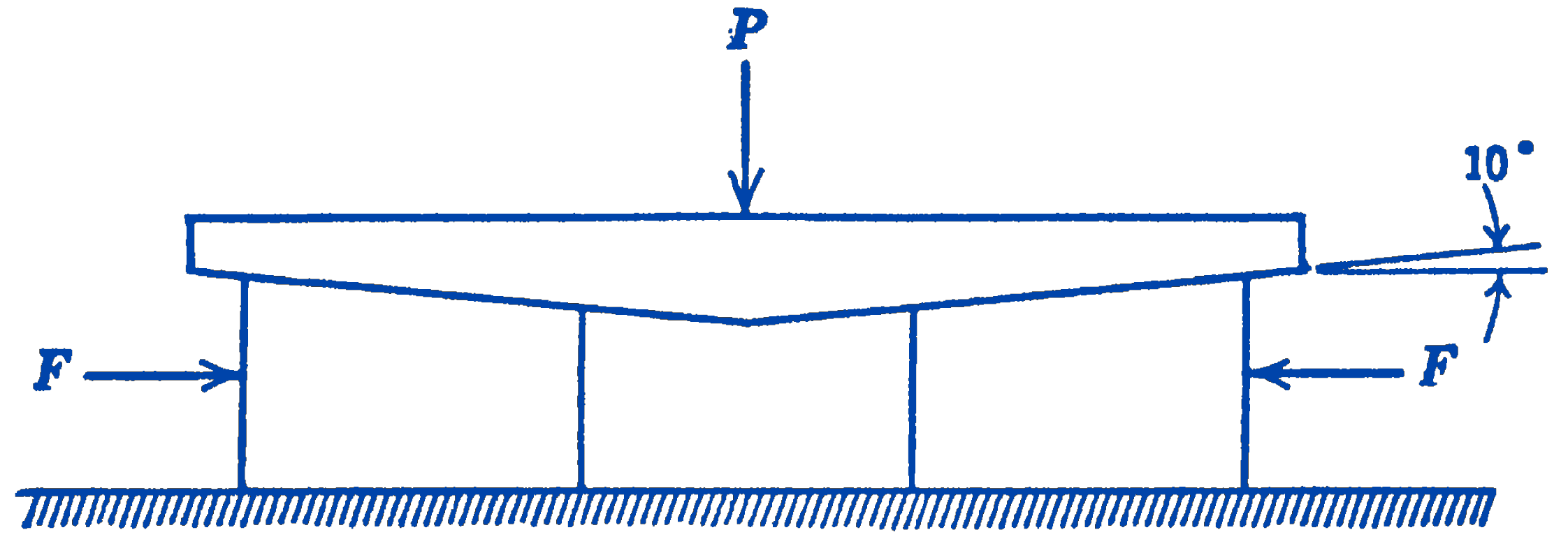
Answer
To raise, \(F=0.348 P\); self-locking