Another type of friction problem frequently occurs in machine design when a flexible member such as a brake-band, cable, or belt passes over or is wrapped around a cylinder. Three typical cases are shown in Fig. 1.
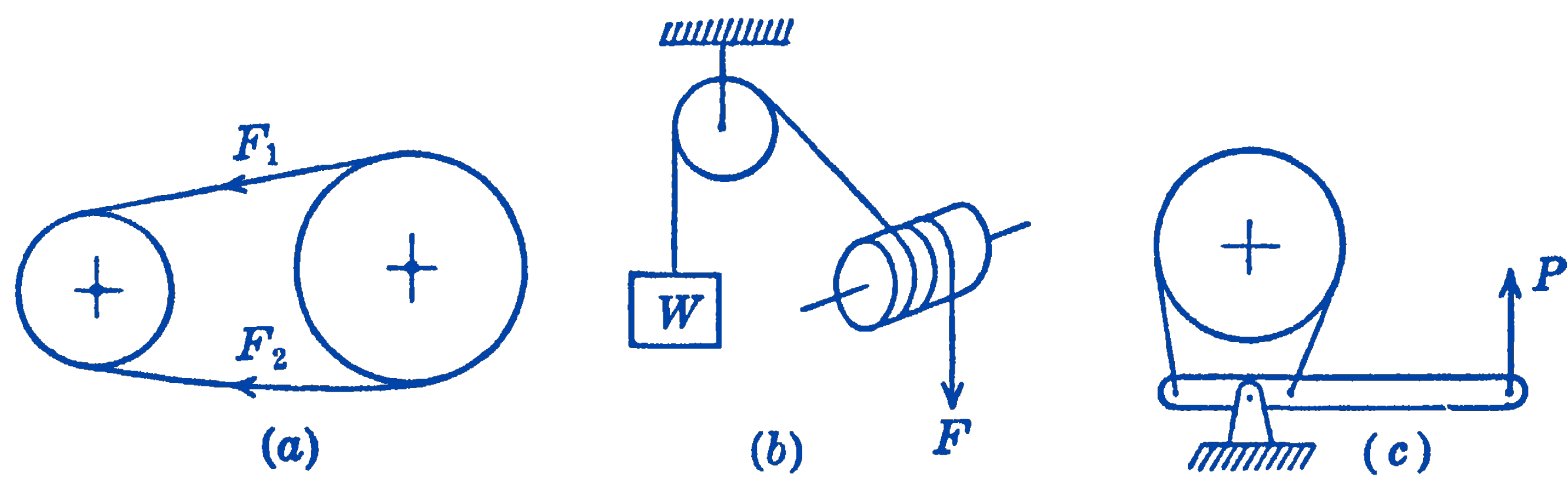
In (a) a belt is shown passing around two pulleys. If there were no friction between the pulley and the belt, the forces \(F_{1}\) and \(F_{2}\) would be equal, and there would be no resultant torque on the pulley and hence no transmitted power. In (b) a weight \(W\) is supported by a cable wrapped around a drum. If there were no friction between the cable and the drum, the force \(F\) would have to be equal to \(W\) for equilibrium. By making use of friction, however, \(W\) can be supported with a much smaller force \(F\). In (c) a rotating pulley is braked by means of a circumferential brake-band which is tightened by means of the lever system and the force \(P\). Because of the friction between the brake-band and the pulley, a torque acts on the pulley to slow it down or to keep it at rest.
In the foregoing examples it will be seen that any condition of rest, relative motion, or impending motion may exist. It is assumed that the coefficient of friction in the following analysis has been taken as the appropriate one for the particular conditions.
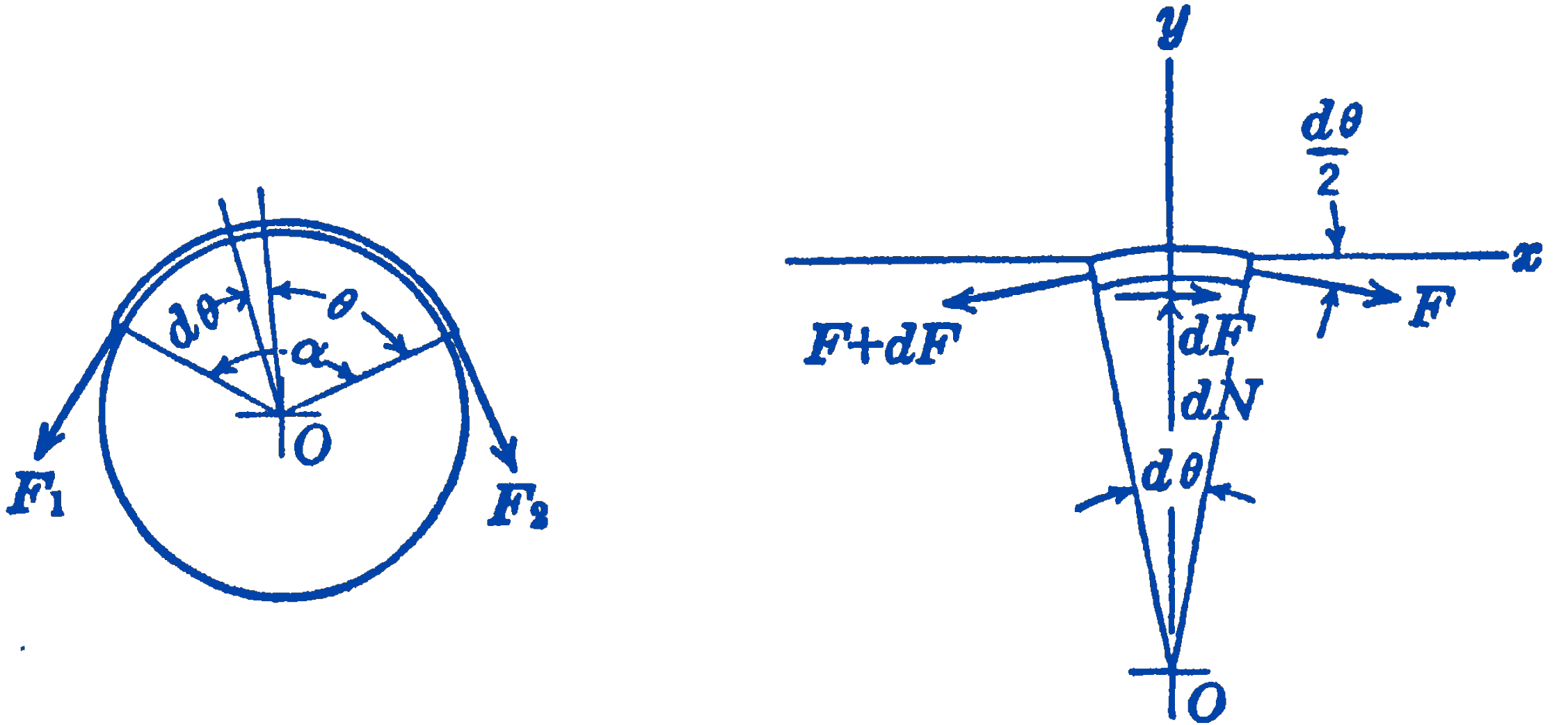
In Fig. 2 we show a portion of a belt or brake-band, and we assume that relative motion is either present or impending so that we can say \(d F=\mu\, d N\), where \(\mu\) is assumed to be constant. The total arc of contact of the band is \(\alpha\), and \(d \theta\) is the infinitesimal angle subtended by the element of the belt shown in the free-body diagram of Fig. 2b. Writing the equations of equilibrium for this element, we have: \[ \begin{aligned} & \sum F_{x}=0=F \cos \frac{d \theta}{2}-(F+d F) \cos \frac{d \theta}{2}+\mu\, d N \\ & \sum F_{y}=0=d N-(F+d F) \sin \frac{d \theta}{2}-F \sin \frac{d \theta}{2} \end{aligned} \] Putting \(\cos \dfrac{d \theta}{2} \approx 1, \sin \dfrac{d \theta}{2} \approx \dfrac{d \theta}{2}\) and dropping second-order differentials, this becomes: \[ \begin{aligned} -d F+\mu\, d N & =0 \\ d N-F\, d \theta & =0 \end{aligned} \] Eliminating \(d N\) : \[ \begin{aligned} \frac{d F}{\mu} & =F\, d \theta \\ \frac{d F}{F} & =\mu\, d \theta \end{aligned} \] Integrating this equation over the whole arc of contact, we obtain: \[ \begin{aligned} \int_{F_{2}}^{F_{1}} \frac{d F}{F} & =\mu \int_{0}^{\alpha} d \theta \\ \ln\frac{F_1}{F_2}&=\mu \alpha \end{aligned} \]
\[ \bbox [5px,border:1px #f2f2f2;background-color:#f2f2f2]{\frac{F_{1}}{F_{2}} =e^{\mu \alpha}} \]
- Notice that to use the above formula, \(\alpha\) must be measured in radians.
Example. What is the minimum force \(P\) required to support the load \(W\) by the cable as shown in Fig. 3? The coefficient of static friction between the cable and the non-rotating cylinder is 0.3.
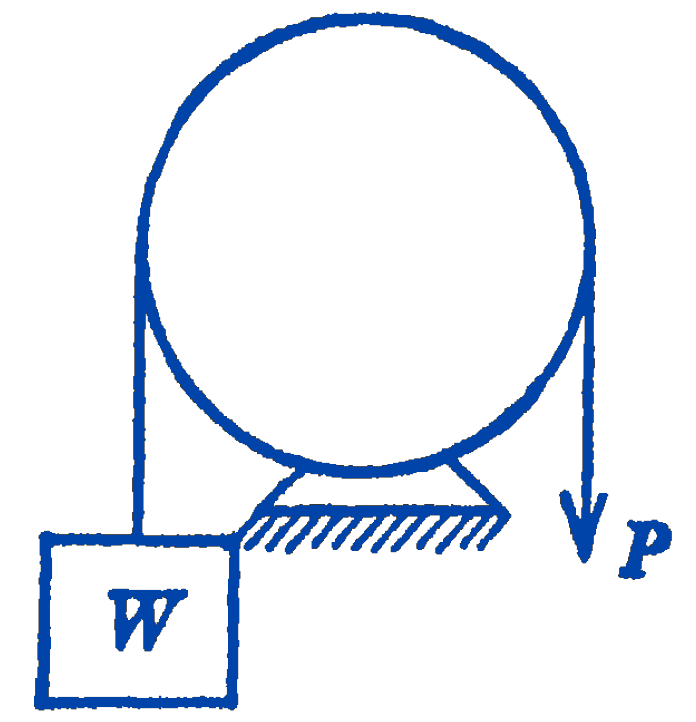
Solution. The minimum force \(P\) will be required when downward motion of \(W\) is impending; hence the coefficient of static friction applies and \(\mu=0.3\). The arc of contact \(\alpha\) is \(180^{\circ}\) or \(\pi\) radians so that: \[ \begin{aligned} \frac{W}{P} & =e^{(0.1) \pi}=2.57 \\ P & =0.389 W \end{aligned} \]
5.7.1 PROBLEMS
1. Referring to Fig. 1b, how many times should the cable be wrapped around the cylinder so that a load \(W\) of 1000 lb can be supported by a force \(F\) of 25 lb? Assume a coefficient of static friction of 0.25.
Answer
2.35 turns
2. Show that the friction torque \(M_{f}\) of a brake-band, in terms of the maximum force in the band \(F_{1}\), is given by the following expression: \[ M_{f}=F_{1} r\left(\frac{e^{\mu \alpha}-1}{e^{\mu \alpha}}\right) \]
3. A hoisting pulley is grooved as shown in the figure. Derive the relationship between the tight and loose sides of the cable, and compare with the case of the flat pulley.
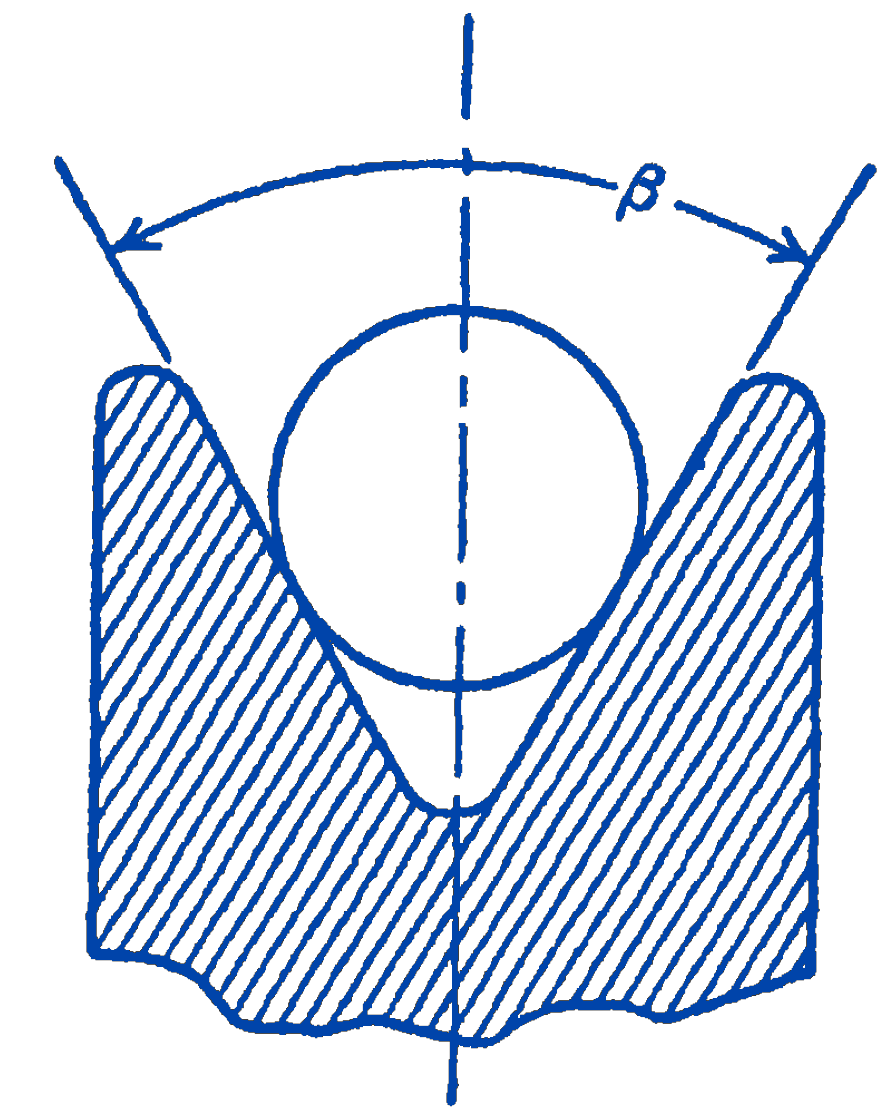
Answer
\(\displaystyle \frac{F_{1}}{F_{2}}>e^{\frac{\mu \alpha}{\left(\sin \frac{\beta}{2}+\mu \cos \frac{\beta}{2}\right)}}\)
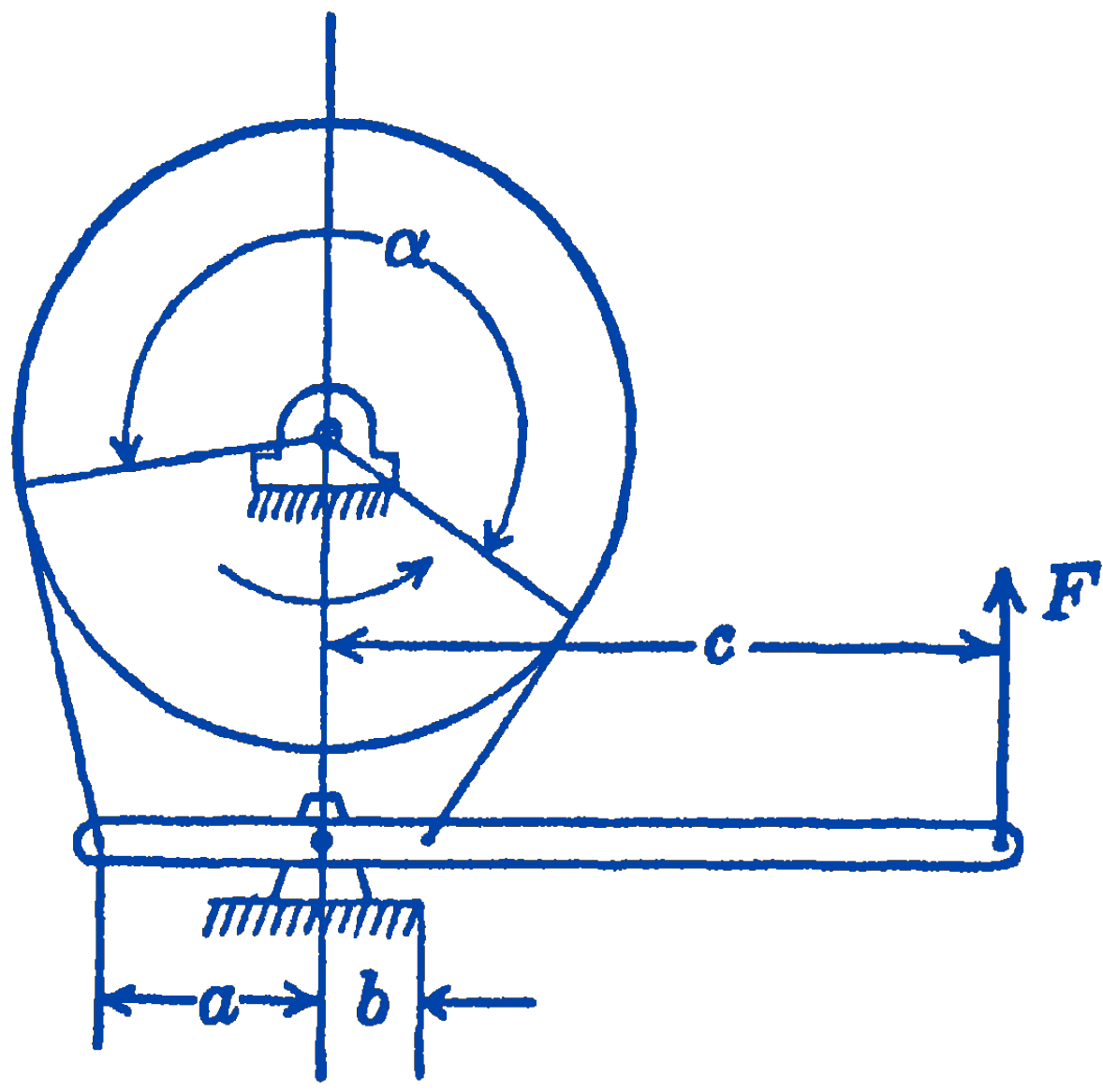
4. What braking force \(P\) is required to exert a friction moment of 1000 in.-lb to prevent clockwise rotation of the drum shown in the figure? The angle of contact is \(200^{\circ}\) and the coefficient of static friction is 0.2 . What would be the required force if the impending motion of the drum were counterclockwise?
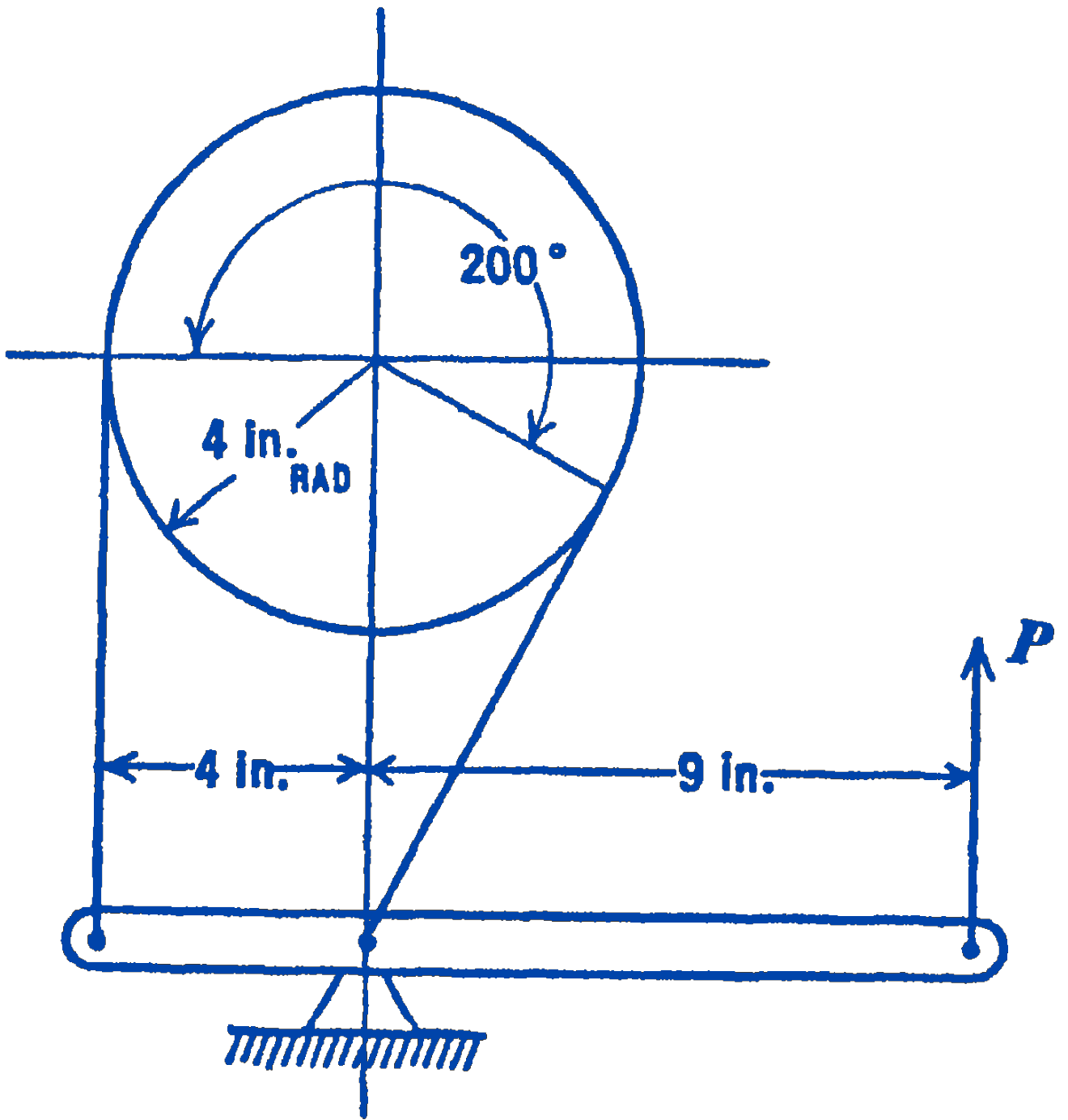
Answer
\(222 \ \mathrm{lb}, 111 \ \mathrm{lb}\)
5. In a differential band-brake, the lever arm is so arranged that the tight side of the band aids the actuating force while the loose side opposes it. Show that such a mechanism can be made so as to permit rotation of the drum in one direction only, while automatically locking in the other direction. Such a device is frequently used on hoists to prevent the load from dropping under its own weight.