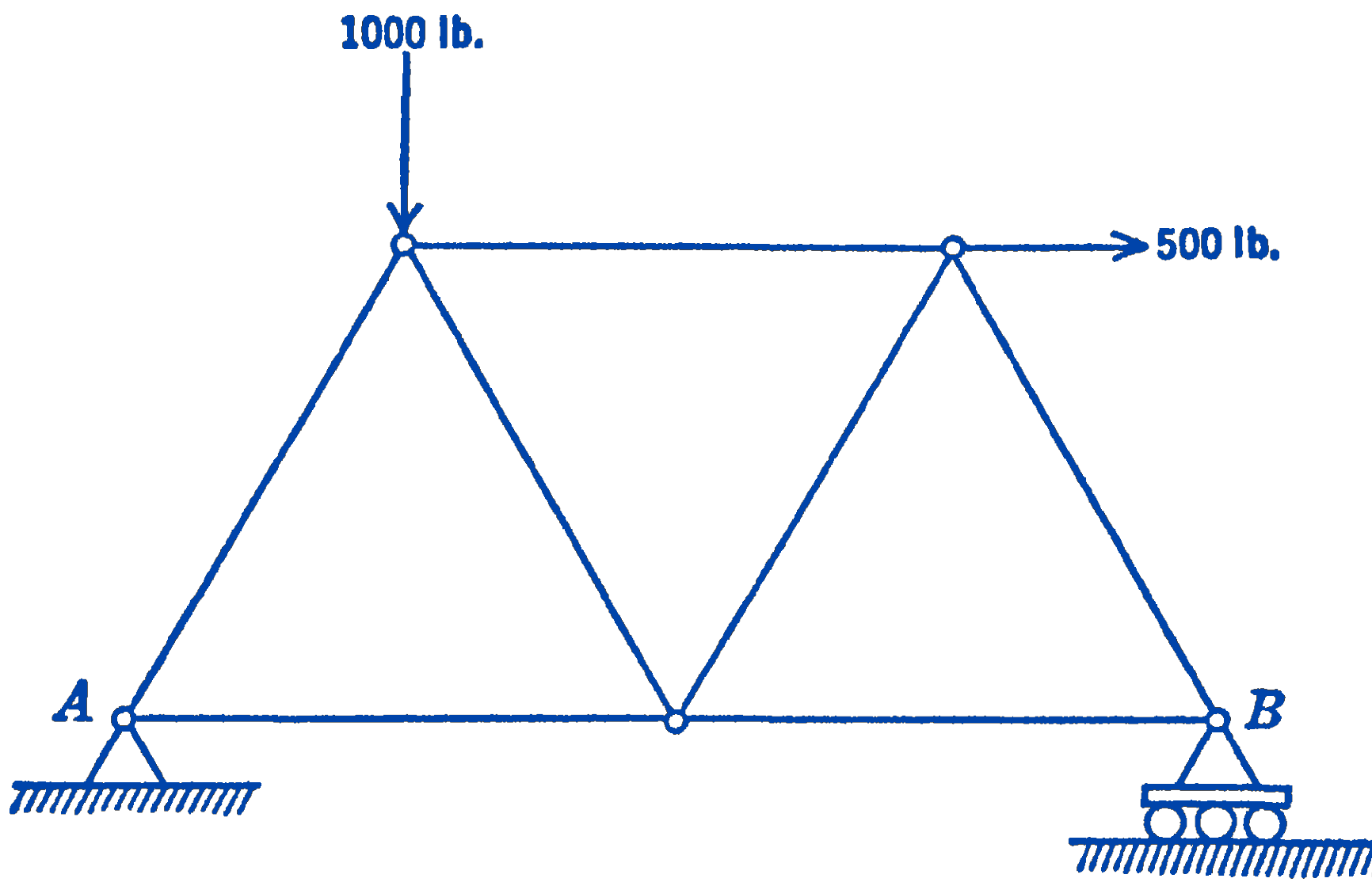
Solution. We first draw a free-body diagram (Fig. 2) of the whole structure:

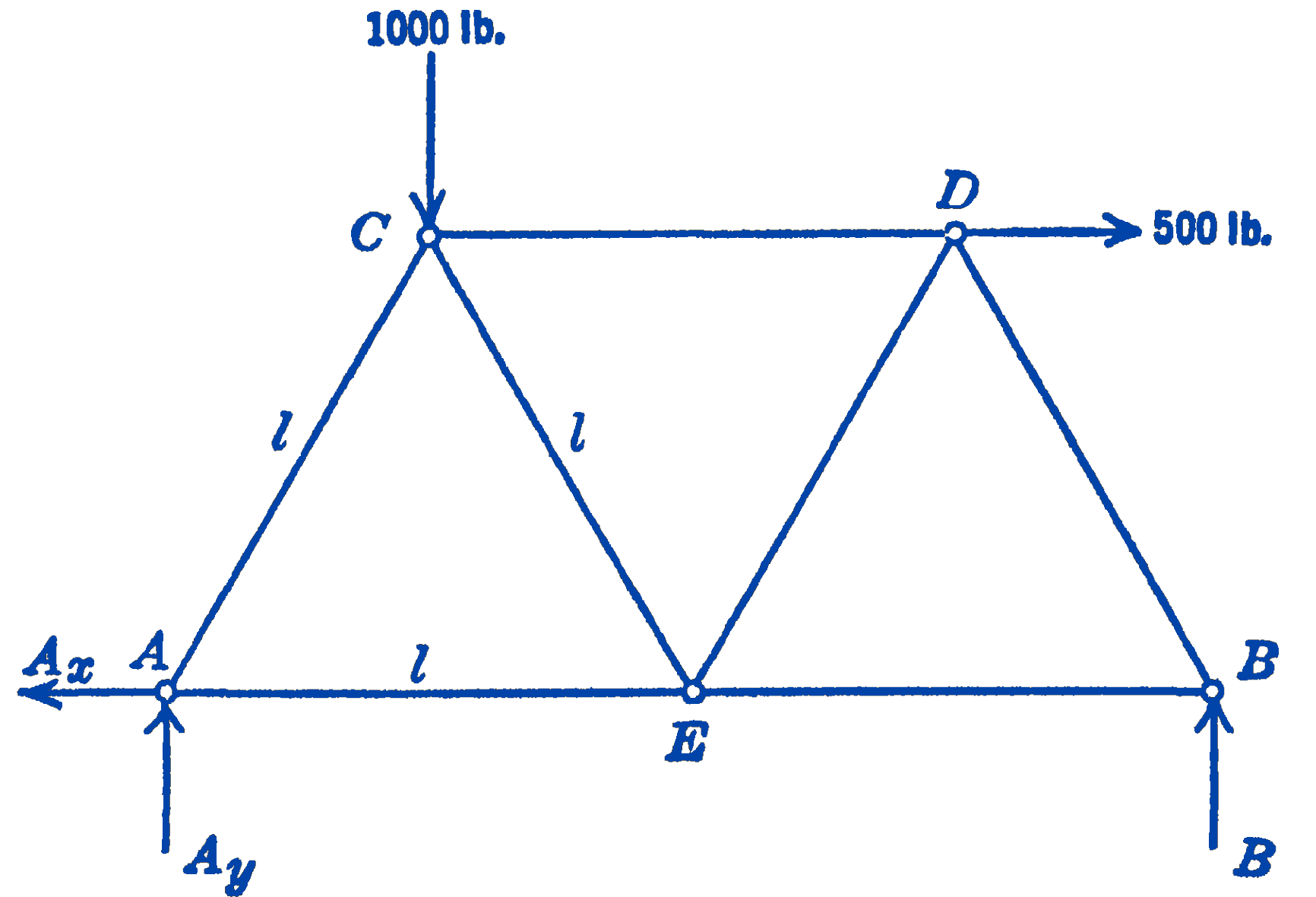
We note that there are no joints which involve only two unknown forces, so that the first step is to determine, from the complete free-body diagram, the external reactions \(A_{x}, A_{y}\), and \(B\).

\[ \begin{aligned} \sum F_{x} & =0=-A_{x}+500 ; \quad A_{x}=500 \mathrm{lb} \\ \sum M_{A} & =0=-\left(\frac{l}{2}\right)(1000)-\left(\frac{\sqrt{3}}{2} l\right)(500)+(2 l) B \\ B & =250+216=466 \mathrm{lb} \\ \sum M_{B} & =0=-(2 l) A_{y}+\left(\frac{3}{2} l\right)(1000)-\left(\frac{\sqrt{3}}{2} l\right)(500) \\ A_{y} & =750-216=534 \end{aligned} \] Check equation:

\[ \begin{gathered} \sum F_{y}=0=A_{y}-1000+B \\ 534-1000+466=0 \end{gathered} \]

Having found \(A_{x}, A_{\nu}\), and \(B\), we can now start at either joint \(A\) or \(B\), since there will be only two unknown forces at each joint. Joint \(A\) :

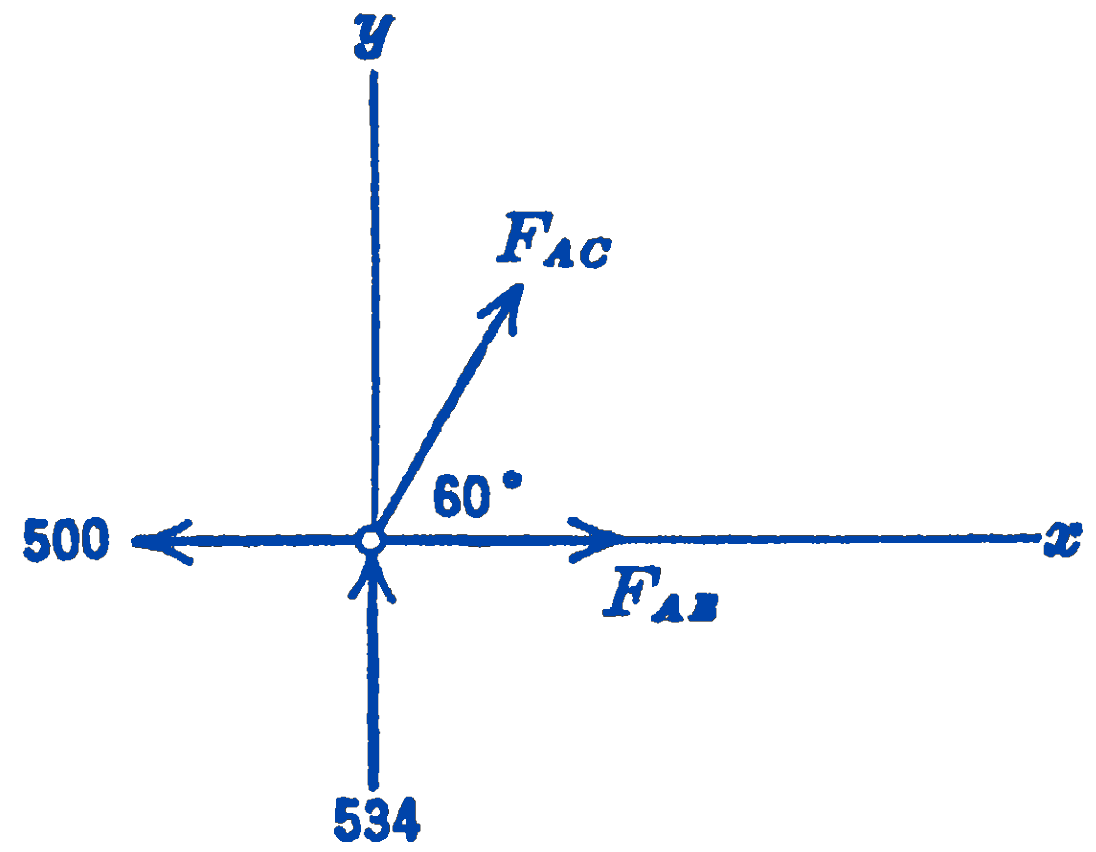
The unknown forces \(F_{A C}\) and \(F_{A B}\) may be either tensions directed away from the joint, or compressions directed toward the joint. For many trusses it will be possible to tell by inspection whether the forces are tension or compression. If this is not possible, the force can be indicated in either direction. If the force then comes out positive, the assumed direction was correct; if it comes out negative, the force was actually reversed. Another procedure, which we will adopt in the present example, is to indicate all unknown forces as tensions. Then, positive forces are tensions, and negative forces are compressions.

Writing down the equations for the free-body diagram of Joint \(A\), we have:

\[ \begin{aligned} \sum F_{x} & =0=-500+F_{A B}+F_{A C} \cos 60^{\circ} \\ \sum F_{y} & =0=+534+F_{A C} \sin 60^{\circ} \\ F_{A C} & =-\frac{534}{(0.866)}=-618\ \mathrm{lb} \text { (compression) } \\ F_{A E} & =500-(-618)\left(\frac{1}{2}\right) \\ & =500+309=809\ \mathrm{lb} \text { (tension) } \end{aligned} \]

Care must be taken to carry the negative sign on the force \(F_{A C}\) through subsequent calculations, as in the \(\sum F_{x}=0\) equation above.

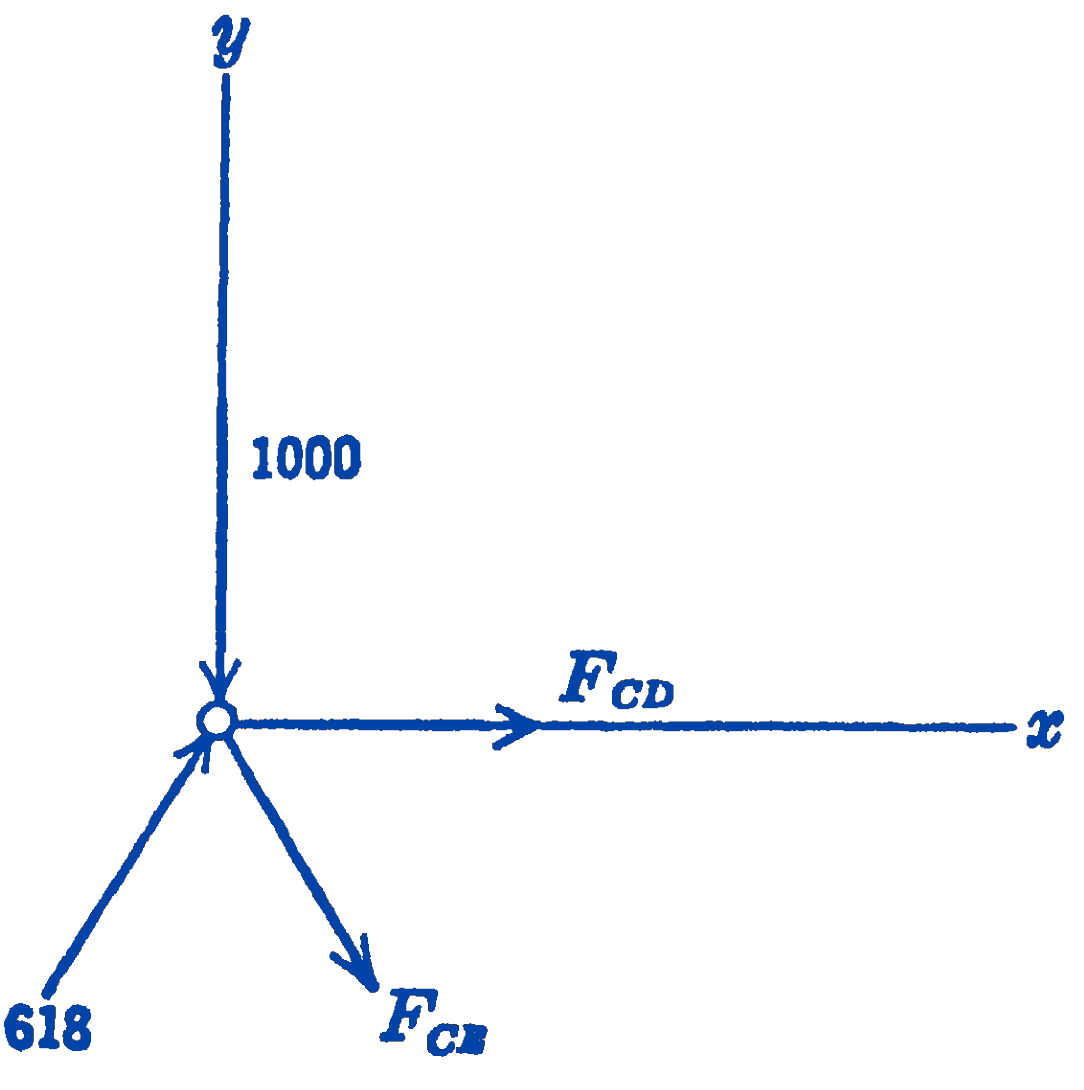
Having found the force \(F_{1 C}\), we can now proceed to the free-body diagram of the Joint \(C\), since there are only two unknown forces left at that joint. Since we now know that \(F_{A c}\) is a compressive force, we shall show it this way in the free-body diagram, rather than carry along the negative sign:

\[ \begin{aligned} \sum F_{x} & =0=F_{C D}+618 \cos 60^{\circ}+F_{C E} \cos 60^{\circ} \\ \sum F_{y} & =0=-1000+618 \sin 60^{\circ}-F_{C E} \sin 60^{\circ} \\ F_{C E} & =\frac{(618)(0.866)-1000}{0.866}=-540\ \mathrm{lb} \text { (compression) } \\ F_{C D} & =-(618)\left(\frac{1}{2}\right)-(-540)\left(\frac{1}{2}\right) \\ & =-309+270=-39\ \mathrm{lb} \text { (compression) } \end{aligned} \]

Proceeding next to Joint \(E\) :

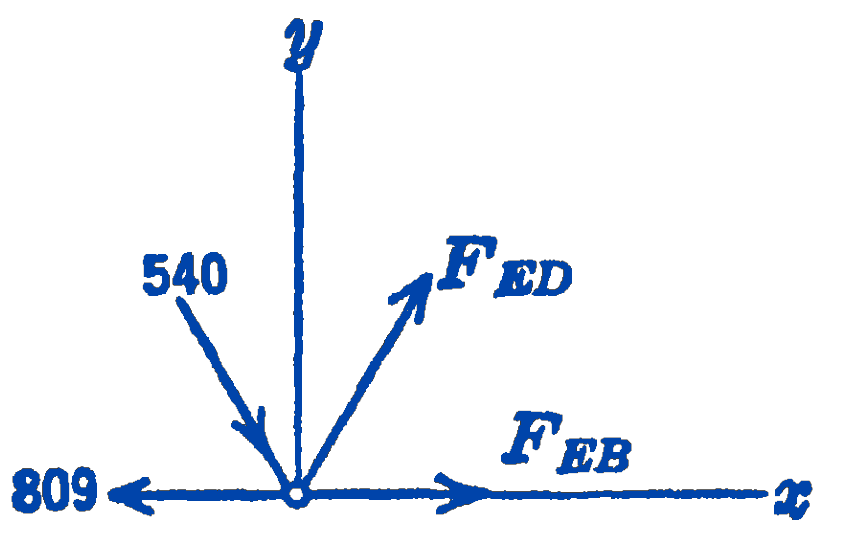
\(\sum F_{x}=0=F_{E B}+F_{E D} \cos 60^{\circ}+540 \cos 60^{\circ}-809\)

\(\sum F_y=0=-540 \sin 60^{\circ}+F_{E D} \sin 60^{\circ}\)

\(F_{E D}=540\ \mathrm{lb}\) (tension)

\(F_{E B}=-(2)(540)\left(\frac{1}{2}\right)+809=269\ \mathrm{lb}\) (tension)

Joint \(D\) :

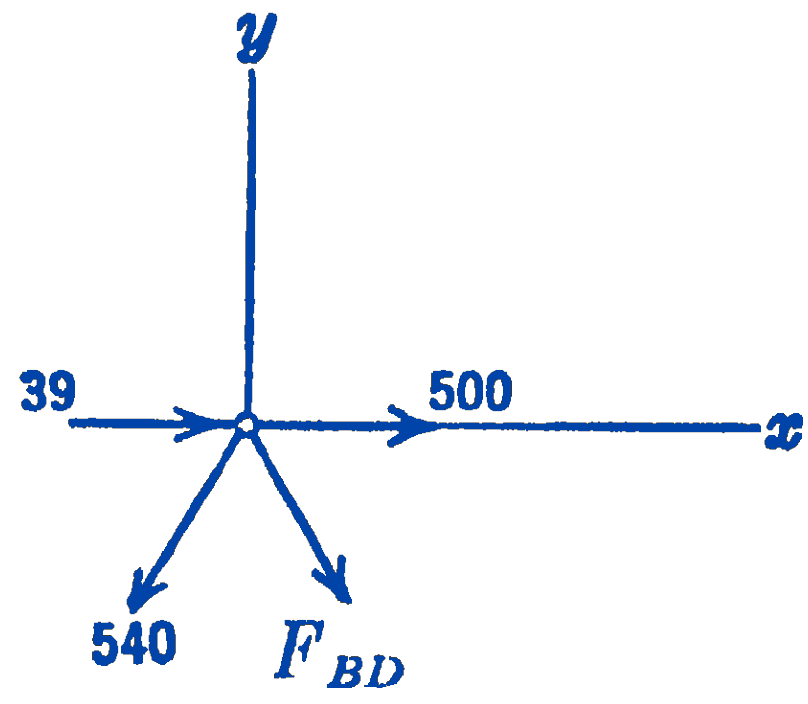
\[ \begin{aligned} & \sum F_{y}=0=-540 \sin 60^{\circ}-F_{D B} \sin 60^{\circ} \\ & F_{B D}=-540\ \mathrm{lb} \text { (compression) } \end{aligned} \]

Check equation:

\[ \sum F_{x}=0=39+500-540 \cos 60^{\circ}-540 \cos 60^{\circ} \] \[539-540 \approx 0\ \text{ checks, to slide-rule accuracy}\]

We have now found the forces in all of the members, although we have not as yet written the two equations for the Joint \(B\). These two equations will serve as additional check equations.

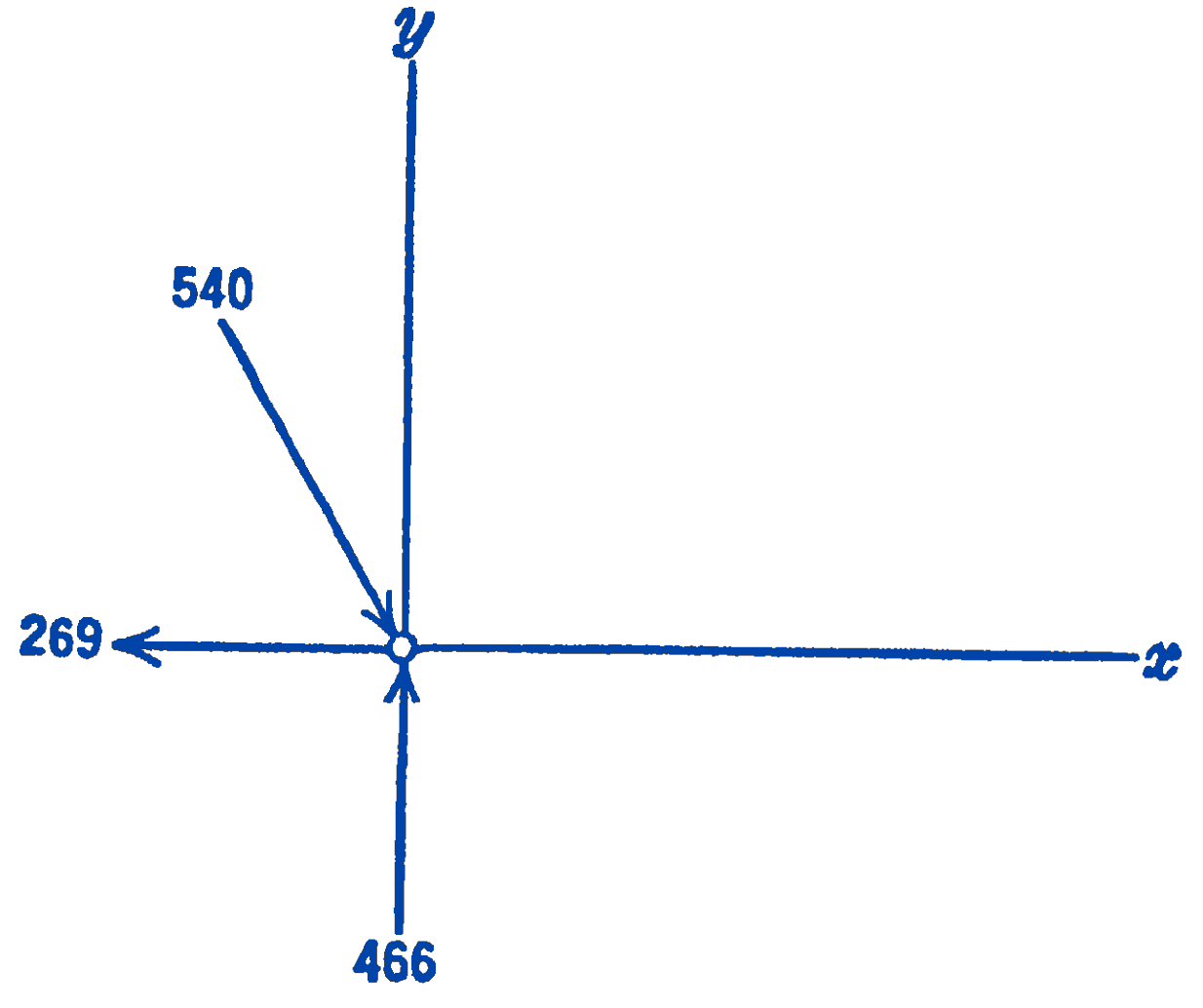
\(\sum F_{x}=0=-269+540 \cos 60^{\circ} ;-269+270 \approx 0\)

\(\sum F_{y}=0=466-540 \sin 60^{\circ} ; 466-466=0\)