If a funicular diagram is drawn for a system of forces which are in equilibrium, it will be found that not only does the force diagram form a closed polygon, but that also the two end strings of the funicular diagram will be colinear, forming a closed funicular polygon, as shown in Fig. 1.
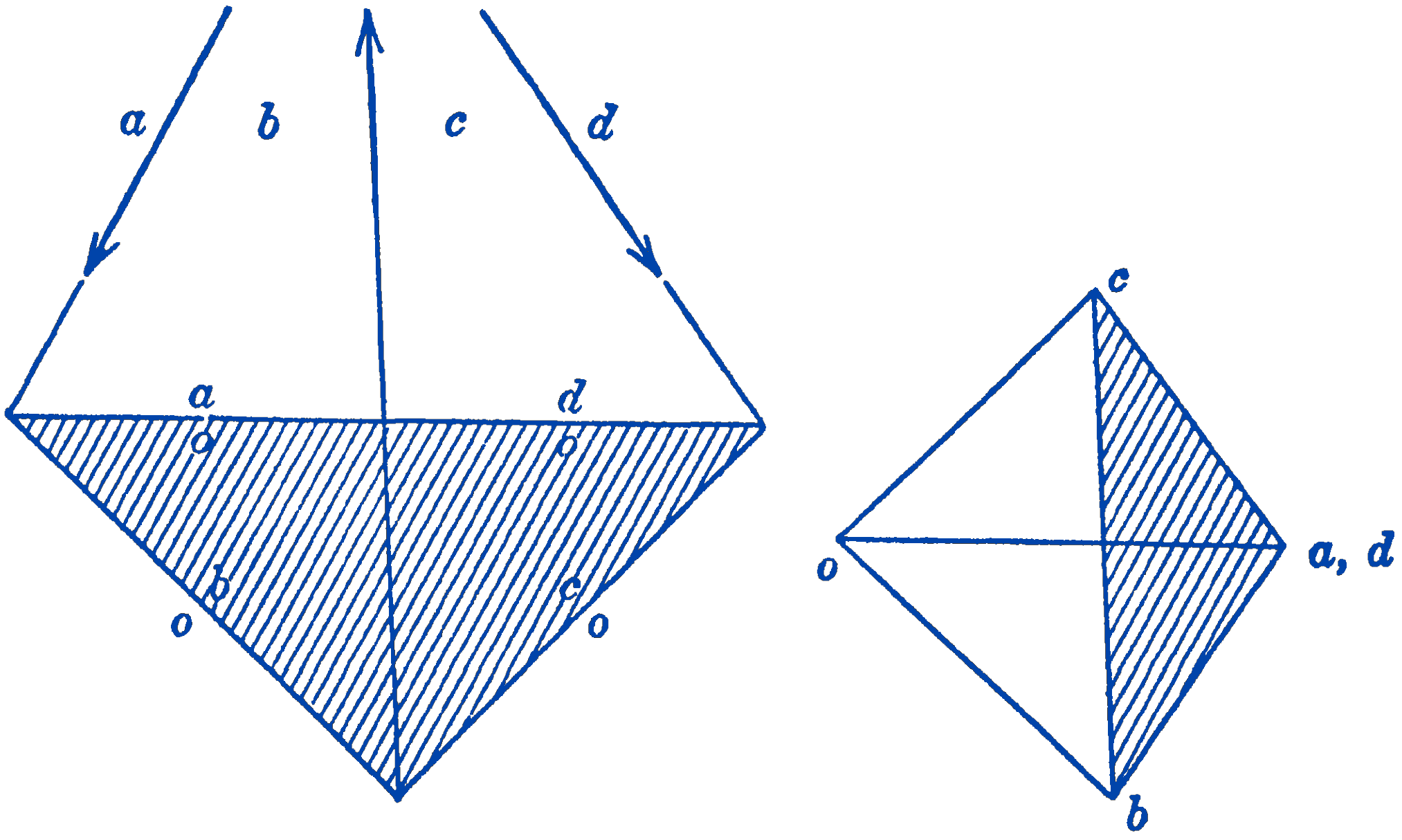
Thus it may be said that the graphical conditions of equilibrium are that both the force polygon and the funicular polygon should close. The closure of the force polygon means that \(\sum F=0\) and the closure of the funicular polygon means that \(\sum M=0\).
We may use the fact that the two diagrams must close to obtain a graphical solution for equilibrium problems, as can be seen from the following example.
Example. Find graphically the reaction forces at \(A\) and \(B\) for a truss loaded as shown in Fig. 2.
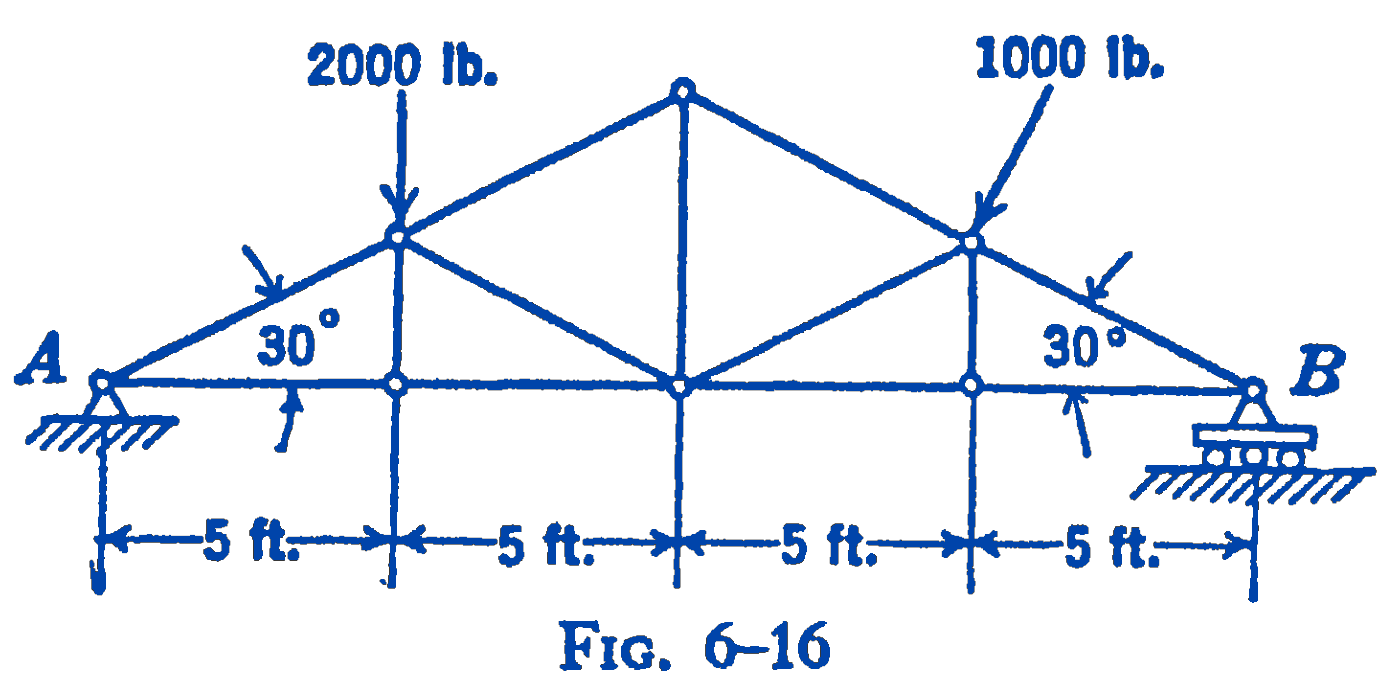
Solution. A free-body diagram of the truss with the forces identified by means of Bow’s Notation is shown in Fig. 3. The unknown forces \(ea\), \(c d\), and \(d e\) are shown with their correct lines of action; their magnitudes, of course, cannot as yet be drawn to scale. The notation should be so arranged that the known forces come first, so that the diagrams can be as completely constructed as possible. The diagram is then drawn to scale, and the force polygon and funicular polygon are constructed with the known forces.
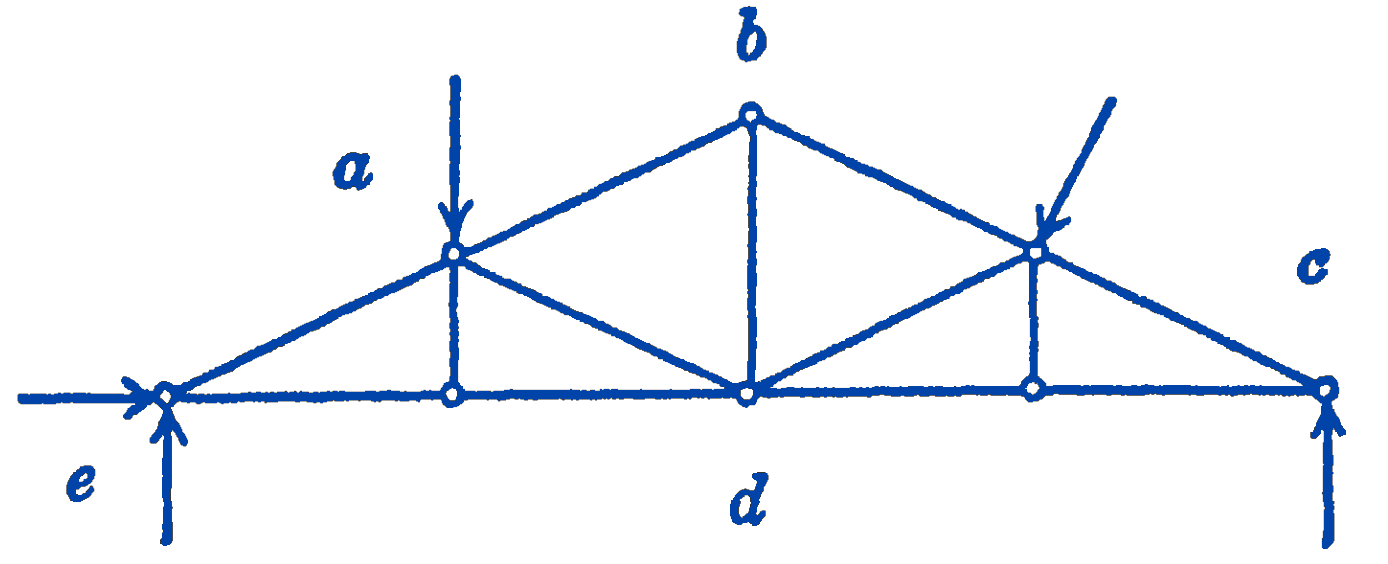
In Fig. 4 we show as much of the force and funicular polygons as can be drawn with the known forces. The complete solution to scale is shown in Fig. 5.
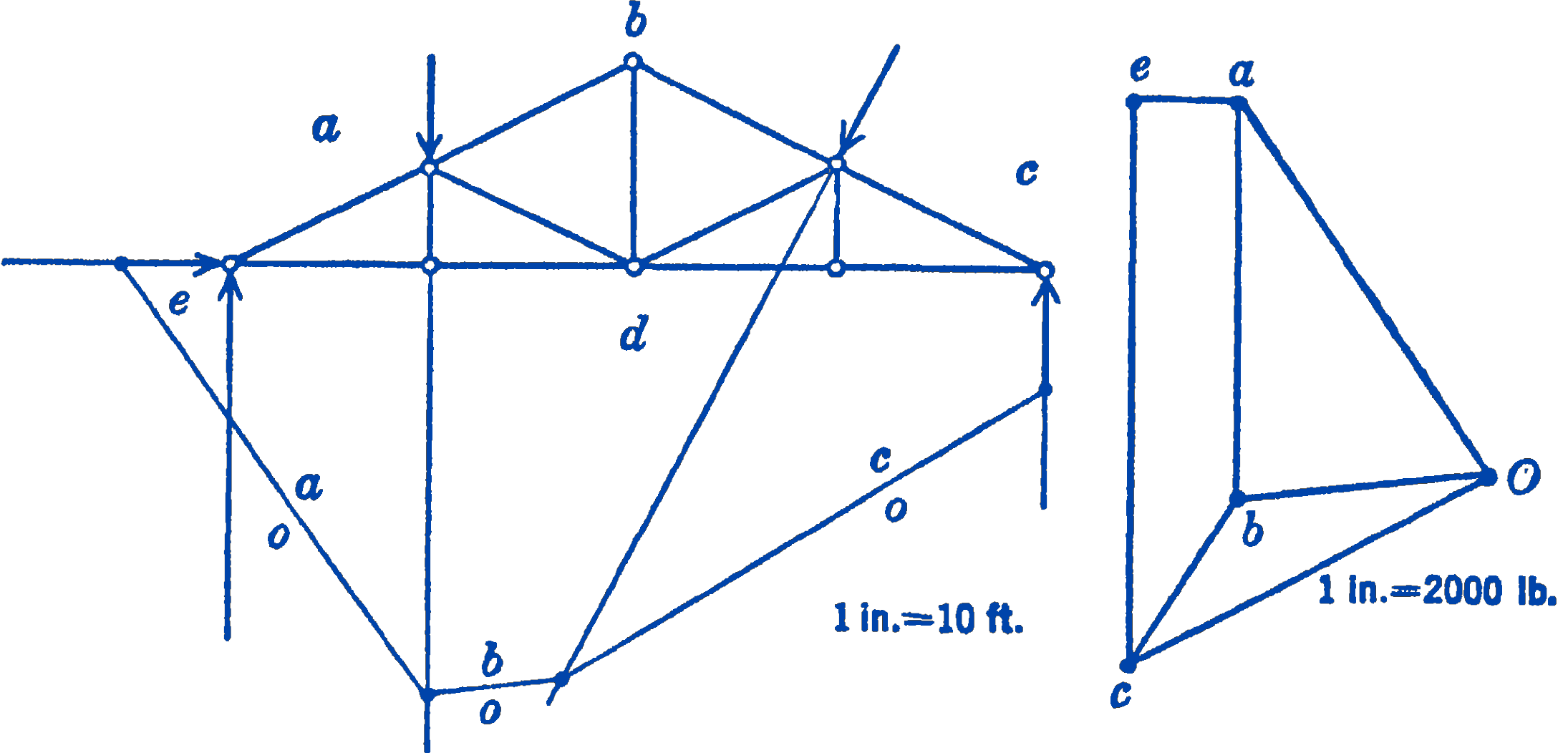
It will be seen from the force polygon of Fig. 4 that it is possible to solve for one of the unknown forces, \(ea\), directly from the force polygon, since it is known that the two forces \(c d\) and de must lie along a vertical line through \(c\), and that the force \(e a\) must lie along a horizontal line through \(a\), for closure of the force polygon. The intersection of these lines fixes the point \(e\), which determines the force \(ea\) and permits us to draw another string, \(eo\), in the funicular polygon. The force polygon is now closed, but the funicular polygon is still open, since the string \(d o\), which would join the points marked \(A\) and \(B\) in Fig. 5, is missing. For equilibrium, this string must be present, however, so we draw do, which closes the funicular polygon. We can now determine the point \(d\) in the force polygon, because, working backwards, we can draw the ray do in the force polygon parallel to the string do in the funicular polygon. Having the point \(d\) in the force polygon gives us directly the forces \(c d\) and \(d e\) and hence completes the solution.
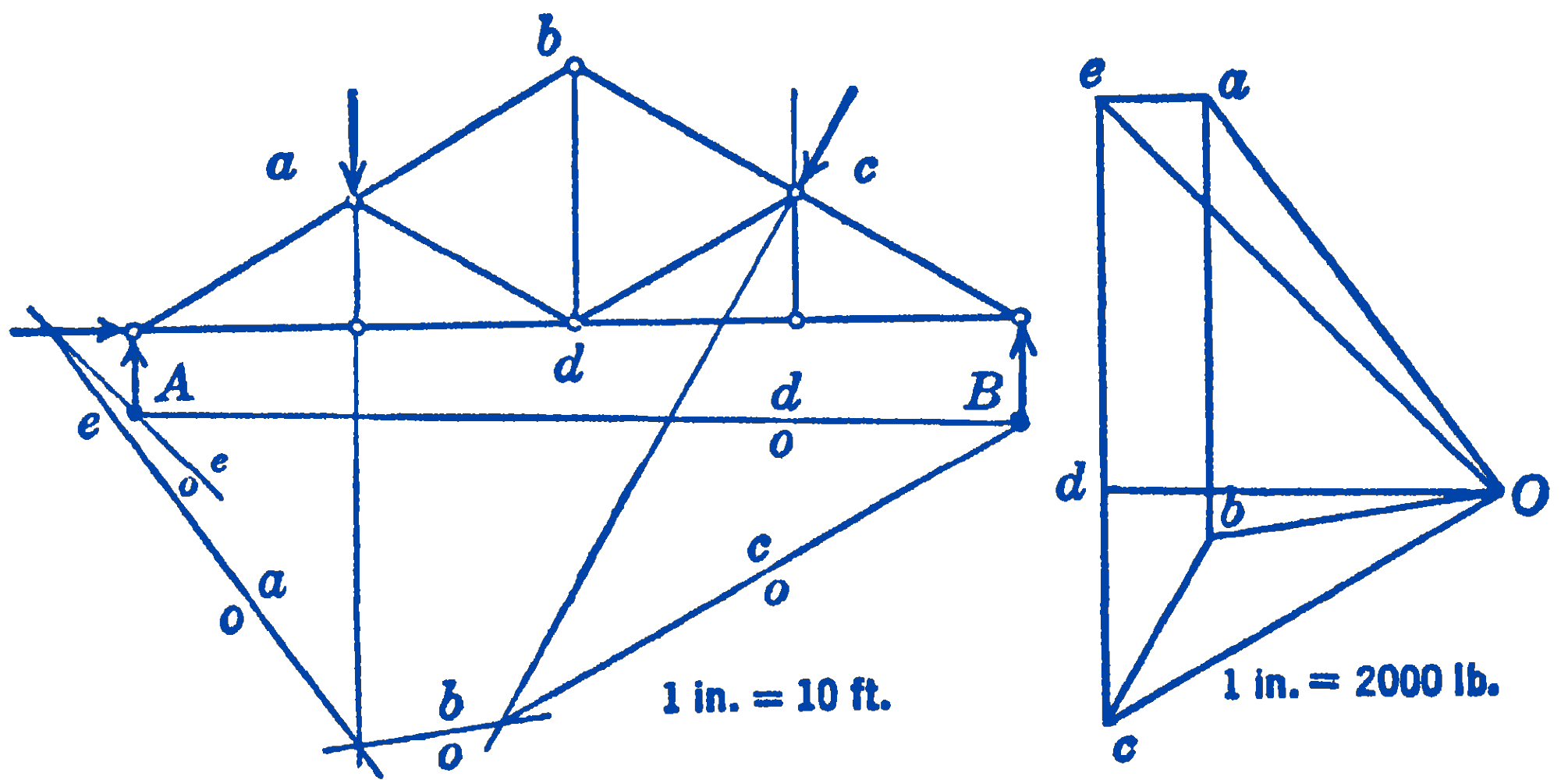
Scaling off the values of the forces, we find: \[ \begin{aligned} & e a=500\ \mathrm{lb} \\ & c d=1070\ \mathrm{lb} \\ & d e=1780\ \mathrm{lb} \end{aligned} \]
To check our solution, let us determine the force \(c d\) analytically by taking moments about the left end of the truss: \[ \begin{gathered} \sum M_{\Delta}=0=(20)(c d)-(5)(2000)-(866)(15)+(500)(2.88) \\ c d=1080\ \mathrm{lb} \end{gathered} \]
6.7.1 Problems
1. A beam is supported at two points and is loaded by three parallel forces as shown in the diagram. Find graphically the two reactions at the supports.
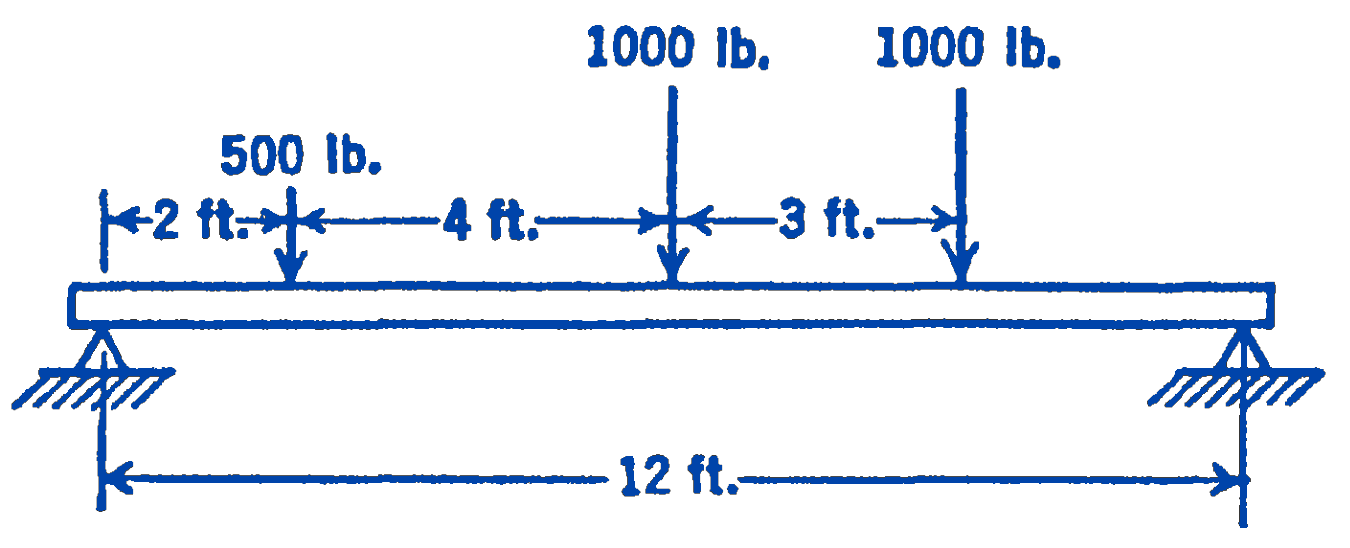
Answer
\(1167 \ \mathrm{lb} ; 1333 \ \mathrm{lb}\)
2. A system of three parallel forces acts on a beam supported as shown in the figure. Find graphically the two reactions at the supports. Check these reactions analytically.
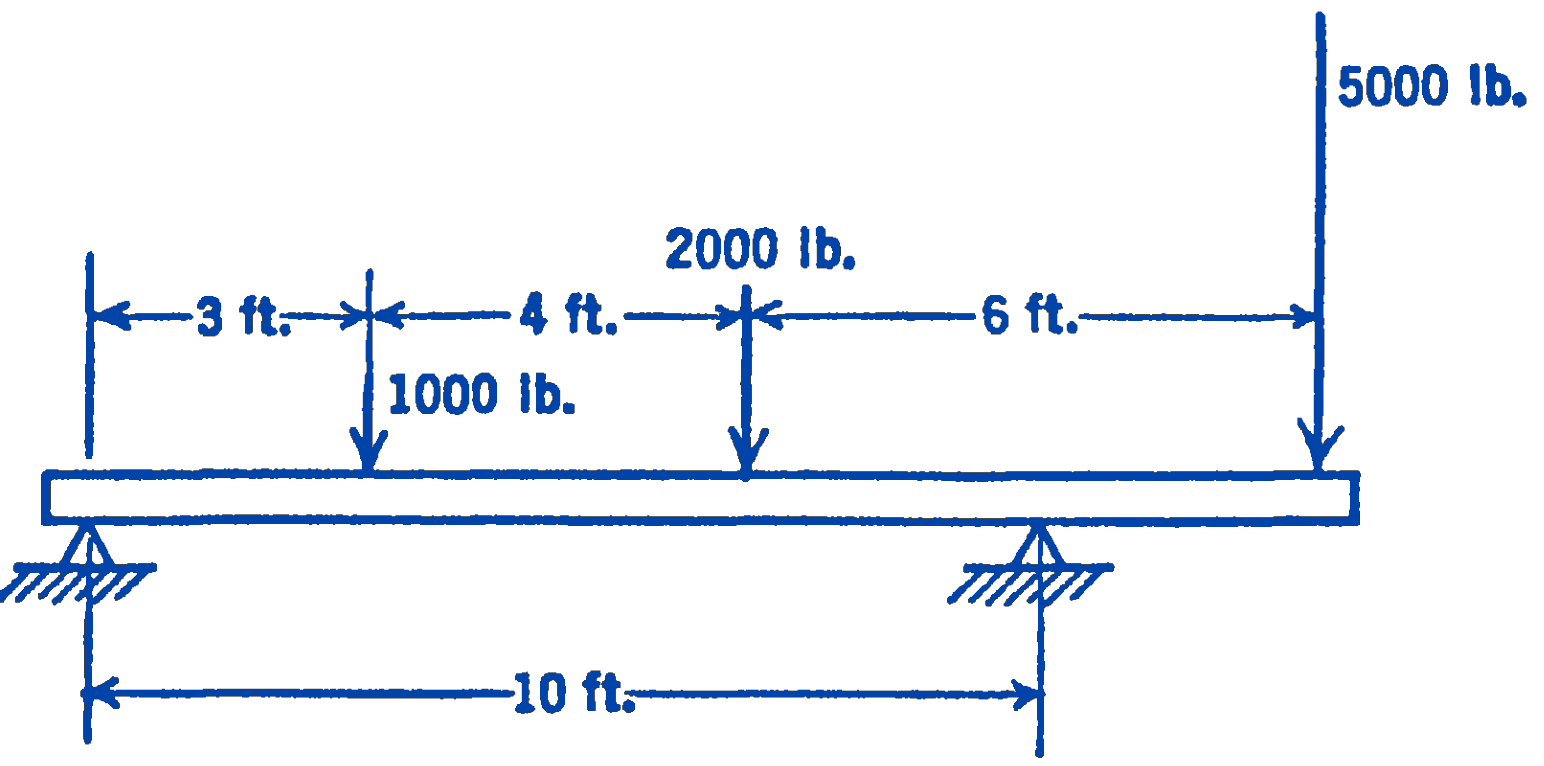
Answer
200 lb (down); 8200 lb (up)
3. A truss is loaded by three forces as shown in the diagram. Find graphically the forces at the supports. Check the value of the vertical reaction at the right end of the truss analytically.
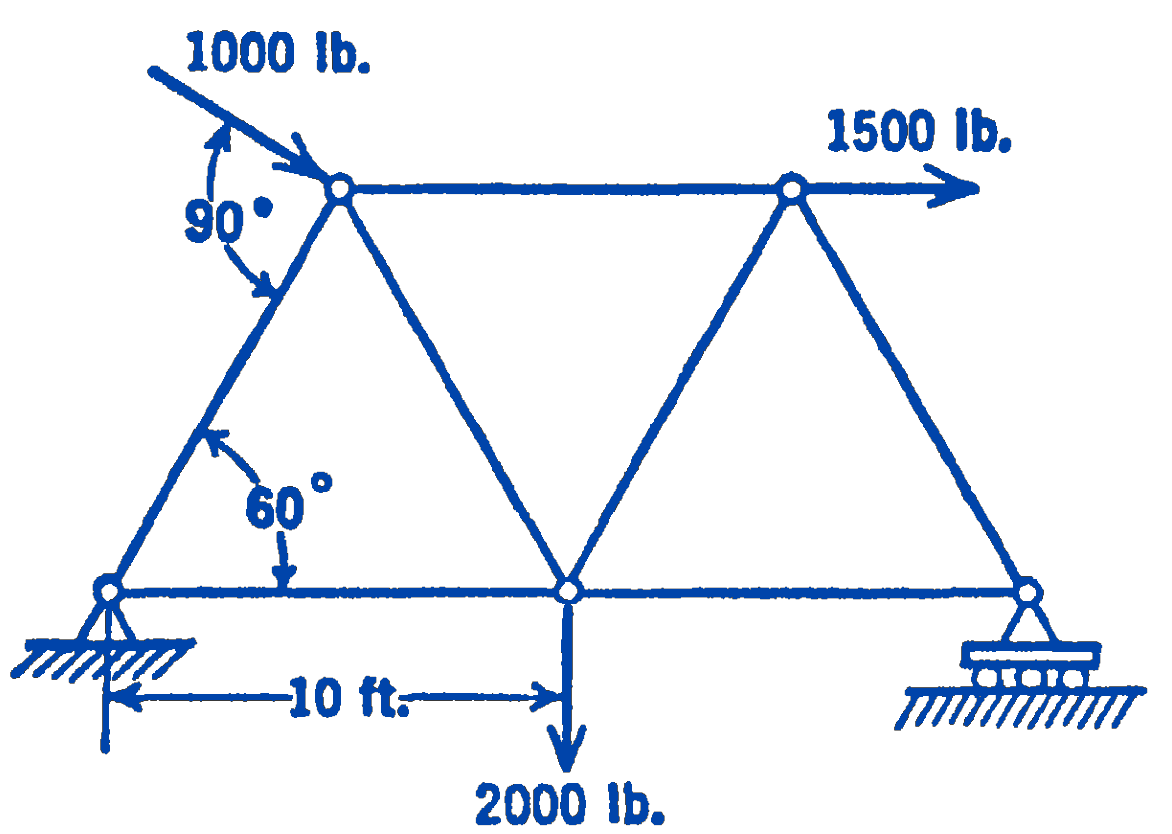
Answer
2150 lb (right end)